无轴承尾桨柔性梁损伤对振动载荷的影响
2022-03-18王伟特张英琦
王伟特,王 磊,张英琦
(1.中国直升机设计研究所,江西 景德镇 333001;2.陆军装备部航空军事代表局驻景德镇地区航空军事代表室,江西 景德镇 333001)
0 引言
无轴承旋翼技术是目前最为先进的旋翼技术之一,它通过复合材料柔性梁的弹性变形取代传统的水平铰、垂直铰和轴向铰,实现桨叶的挥舞、摆振和变距运动。这种旋翼形式具有结构简单、零件数量少、重量轻、可靠性和安全性高等优势,对直升机旋翼系统发展具有较大的意义。
无轴承旋翼采用复合材料桨叶,主要是由于复合材料具有各向异性和性能可设计性等特点,使得其在制造中具有较大的优势。而复合材料在制作、铺贴和固化过程中容易产生脱粘、压陷、空隙、疏松、夹杂、富胶、贫胶等缺陷问题,当复合材料桨叶在实际工作过程中受到机体振动和复杂气动环境的作用时,这些缺陷可能发展成损伤。损伤形式主要包括分裂、分层、拉丝断裂、穿孔等,损伤进一步恶化,会造成部件破坏,危及直升机飞行安全。因此,必须保证桨叶在使用过程中不发生安全问题。
柔性梁是无轴承桨叶的主要部件之一,其制造缺陷和使用磨损会使旋翼系统各片桨叶的质量、刚度、阻尼和气动特性等方面发生差异。而直升机在实际飞行时,弹性桨叶在周期气动激振力作用下产生动载荷,其桨根的振动载荷会通过桨毂传递至机身。当桨叶差异较大时,桨根的振动载荷会迅速增大,整个旋翼系统就会发生故障,不仅会影响桨叶的振动特性,而且会对全机的振动响应产生较大影响。因此,本文主要对无轴承尾桨柔性梁损伤后形成的差异旋翼进行仿真分析,以得出柔性梁损伤程度及损伤位置对尾桨振动载荷的影响规律。本研究不仅可以为无轴承尾桨外场振动异常提供一定的理论支撑,对差异旋翼振动降低提供一定指导,也为以后差异旋翼研究提供一定的思路。
1 计算模型
本文主要对无轴承尾桨柔性梁损伤形成的差异旋翼系统进行建模分析,主要包括结构模型、气动模型和分析方法。
在进行建模时桨叶采用二阶非线性及结构阻尼的弹性梁模型;柔性梁采用大变形梁进行精确计算;柔性梁与桨叶则通过支撑轴承进行连接,形成双路传力路径。桨叶与柔性梁被离散为具有多个自由度的梁单元,基于Hamilton原理建立桨叶运动和变形之间的关系。在计算动态载荷时,采用准定常理论,其升力系数、阻力系数、力矩系数随马赫数、攻角的变化取自风洞吹风翼型数据表;桨叶尾迹模型采用非均匀入流自由尾迹进行计算。桨叶剖面载荷由外段桨叶的惯性力与气动力沿桨叶展向积分得到,再通过力积分方法将载荷点外段载荷累加到结构载荷,得到桨根段的各阶谐波载荷。最后,根据桨毂力合成理论,将各片差异桨叶的桨根各阶谐波载荷合成尾桨中心的振动载荷。本文技术路线见图1。
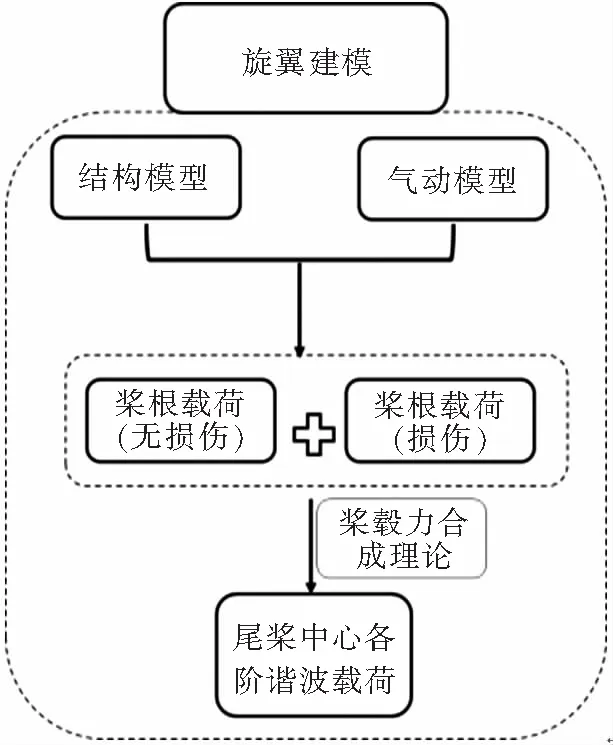
图1 技术路线
1.1 柔性梁破坏模式
本文只针对柔性梁不同纤维层分层失效破坏模式进行分析。柔性梁分层破坏断口形貌如图2所示。当柔性梁纤维层破坏时,其截面的挥舞刚度、摆振刚度和扭转刚度会发生不同程度的损失。假设柔性梁端口截面为矩形截面,柔性梁高度为,柔性梁宽度为,柔性梁损伤高度′,如图3所示。

图2 柔性梁断口形貌图

图3 柔性梁矩形剖面图
矩形剖面的挥舞刚度、摆振刚度和扭转刚度理论公式如下:

(1)

(2)
=
(3)
其中′为柔性梁损伤的高度占比,可用来表示柔性梁损伤程度。根据上述公式,可以推导柔性梁剖面刚度的损失情况。表1中给出了不同损伤程度下柔性梁剖面刚度的变化情况。
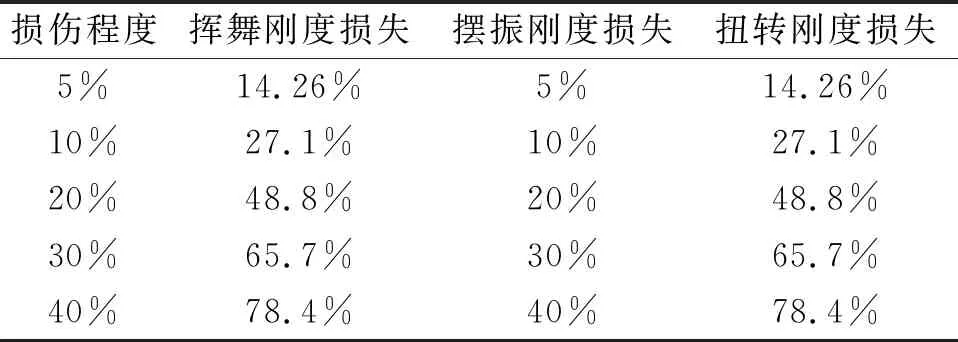
表1 不同损伤程度柔性梁剖面刚度变化情况
1.2 柔性梁损伤位置
该无轴承尾桨的柔性梁总长度为500 mm;进行柔性梁损伤分析时,设置损伤区域的宽度为13 mm。损伤位置主要采用四个典型位置。分布示意见图4。距离桨毂中心距离见表2。损伤位置1位于柔性梁中央夹持区终止位置;损伤位置2位于柔性梁夹持区与支撑轴承中间区间位置;损伤位置3位于支撑轴承附近位置;损伤位置4位于靠近柔性梁主要变形区位置。
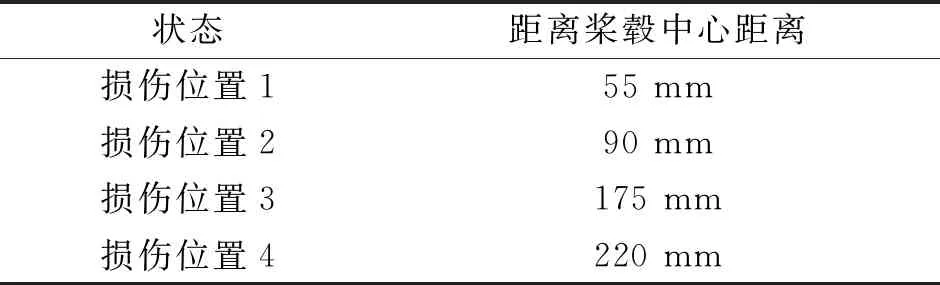
表2 柔性梁不同损伤位置表

图4 损伤位置示意图
1.3 尾桨桨毂力合成
下面给出各片尾桨叶对桨毂作用力公式。桨叶作用在桨毂上的力的分量如图5所示。
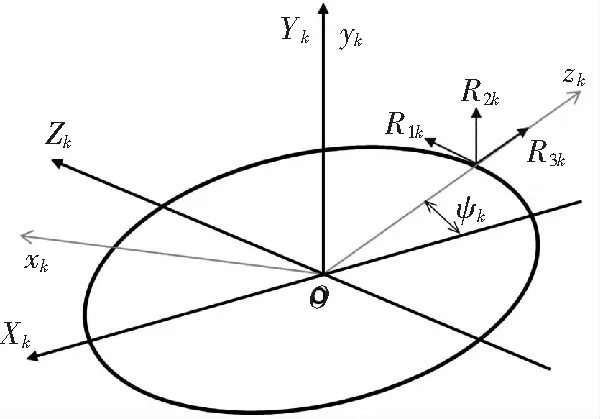
图5 第k片桨叶作用在桨毂上的力的分量
其中第片桨叶作用在桨毂的力分别为1、2、3。1、2、3是随方位角变化的周期函数,可以表示成傅氏级数的形式,如下式所示:


(4)

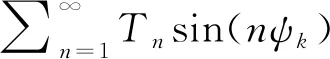
(5)


(6)
单片桨叶作用力在旋翼构造轴系上的分量为:
=1sin-3cos
(7)
=1cos+3sin
(8)
=2
(9)
桨毂平面内的分力:
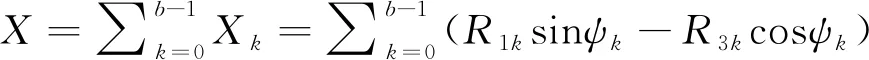
(10)
升力方向的力:

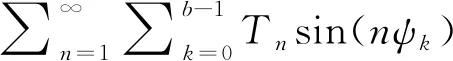
(11)
其中为桨叶片数。
对于理想旋翼,桨叶升力方向频率为、2、3…的谐波力通过桨毂,只有桨叶片数整数倍的谐波力项传给机身(=1,2,3…),其余谐波力在桨毂上相互平衡。桨叶作用到桨毂上旋转面侧向力及力矩的各阶谐波量,只有当谐波频率=(±1)时,才能传到机体上去。
对于差异旋翼,各片桨叶幅值和相位存在偏差,因此机体上会出现旋翼的各阶谐波。
1.4 计算方法
无轴承尾桨的传力路径为双路传力,柔性梁和袖套分别为两条传力路径,支撑轴承为一个连接点。柔性梁取代铰接式构型的挥舞铰、摆振铰以及扭转铰,实现桨叶挥舞、摆振和变距运动。本文利用CAMRADII计算单片桨叶的桨根载荷情况。图6为无轴承尾桨的计算模型。

图6 无轴承尾桨计算模型
在进行差异桨叶的振动载荷分析时,主要采用CAMRADII计算柔性梁不同损伤程度下单片桨叶的桨根力;其次利用桨毂力合成理论求出时域下差异桨叶的振动载荷;最后求解差异桨叶尾桨毂中心的各阶谐波载荷。
2 计算结果与分析
2.1 柔性梁损伤程度对载荷的影响分析
本文对某型机的尾桨进行分析,桨叶片数为4片,其中一片柔性梁发生损伤,其他三片保持正常,分析其差异旋翼振动载荷的变化情况。
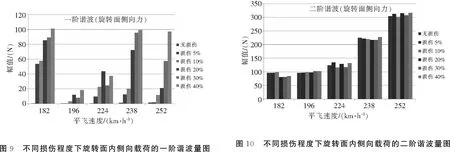
下面分析单片桨叶柔性梁不同损伤程度下尾桨毂中心载荷的变化情况。柔性梁损伤位置在中央夹持区域终止位置处,即损伤位置1,损伤宽度13 mm。计算了不同平飞速度下其尾桨载荷的变化趋势。表3中给出了飞行速度和尾桨距。表4、图7和图8为不同损伤程度下尾桨中心升力方向的各阶谐波量。表5、图9和图10为不同损伤情况下尾桨旋转面内侧向载荷的各阶谐波量。

表3 飞行速度及尾桨距
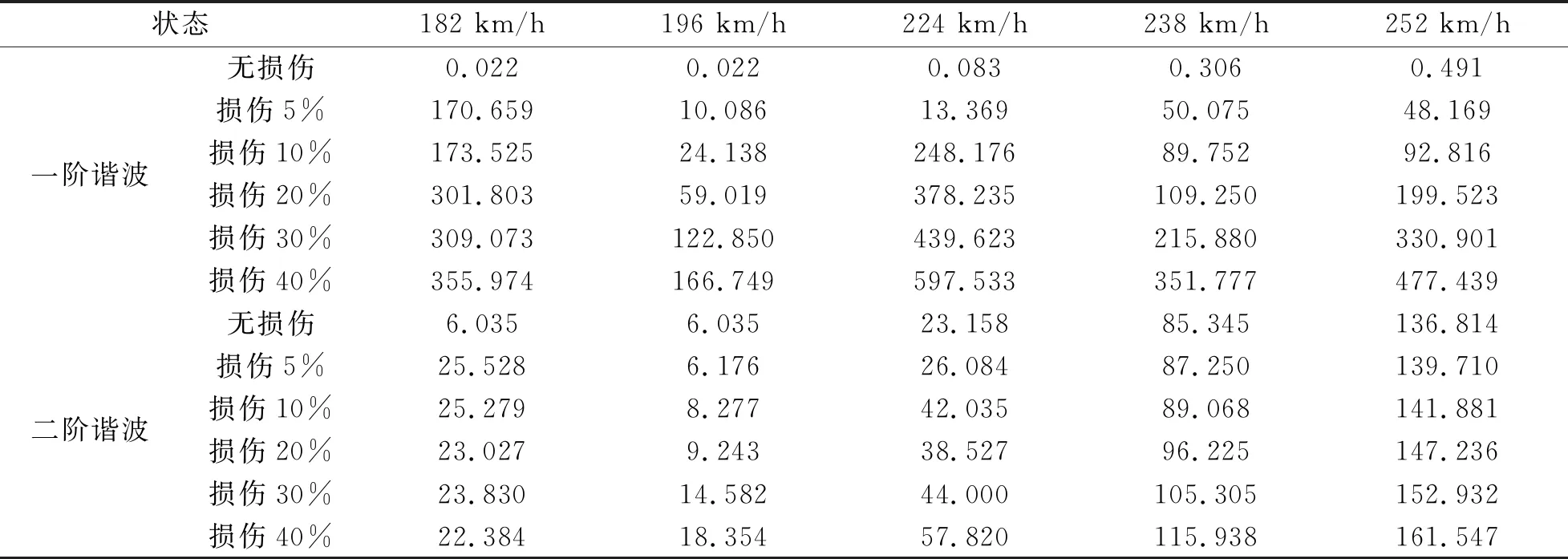
表4 不同损伤程度下尾桨中心升力方向的各阶谐波量

表5 不同损伤程度下尾桨旋转面内侧向载荷的各阶谐波量

续表5
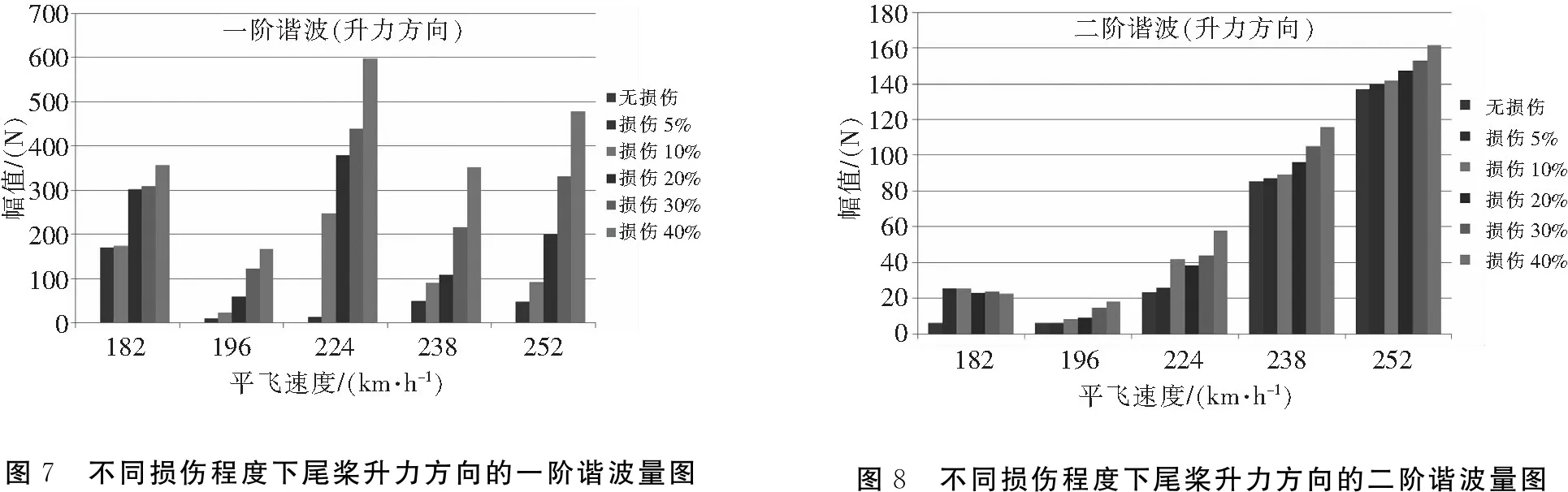
由图7和图8可知:①同一飞行速度下,随着柔性梁损伤程度的增大,其升力方向载荷的一阶谐波和二阶谐波也逐渐增大;②升力方向载荷的二阶谐波随着飞行速度的增大,其数值迅速增大。
由图9可知,随着损伤增大,其旋转面内侧向载荷的一阶谐波也逐渐增大。由图10可知,旋转面内侧向载荷的二阶谐波主要与飞行速度相关,而与柔性梁损伤程度的相关性较弱。
2.2 柔性梁损伤位置对载荷的影响分析
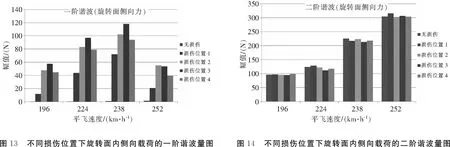
下面分析相同损伤程度下,不同损伤位置对尾桨中心振动载荷的影响。柔性梁损伤程度选取20%,损伤位置为四个典型的损伤位置。表6、图11和图12给出了不同损伤位置下尾桨中心升力方向载荷的各阶谐波量。表7、图13和图14给出了不同损伤位置下尾桨旋转面侧向载荷的各阶谐波量。

表6 不同损伤位置下尾桨中心升力方向的各阶谐波量

续表6
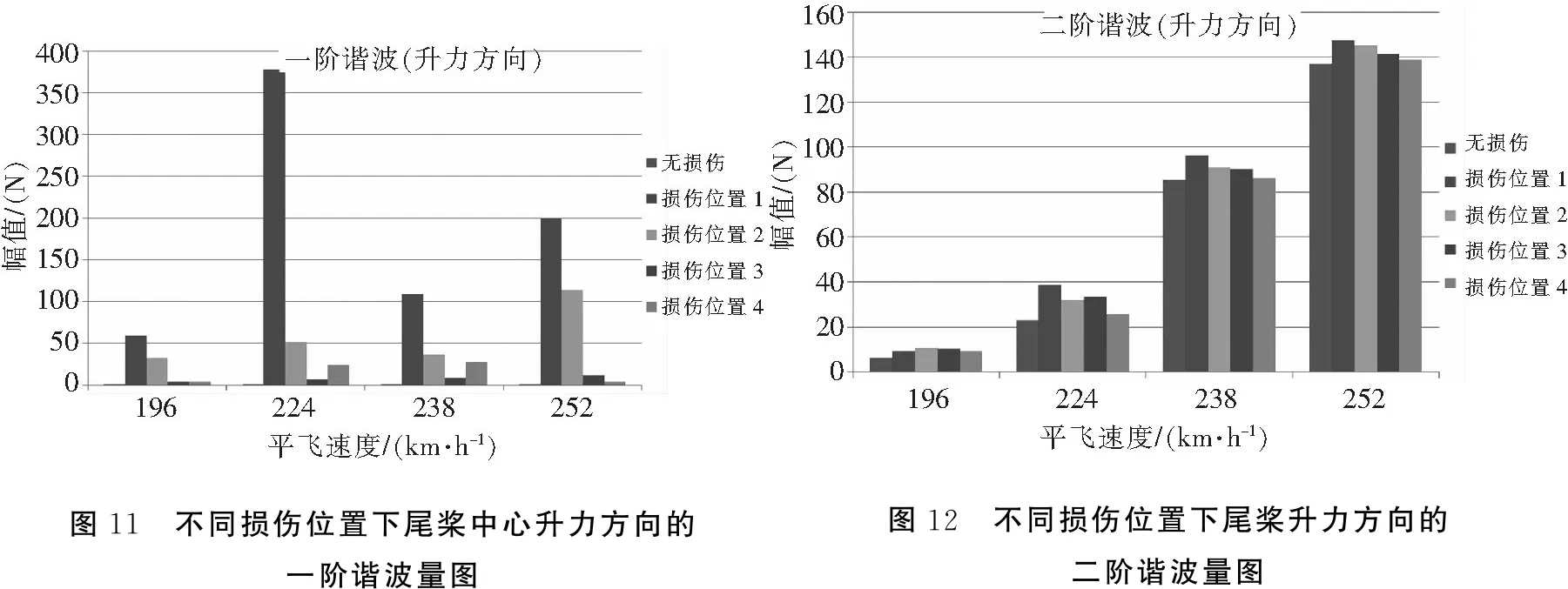
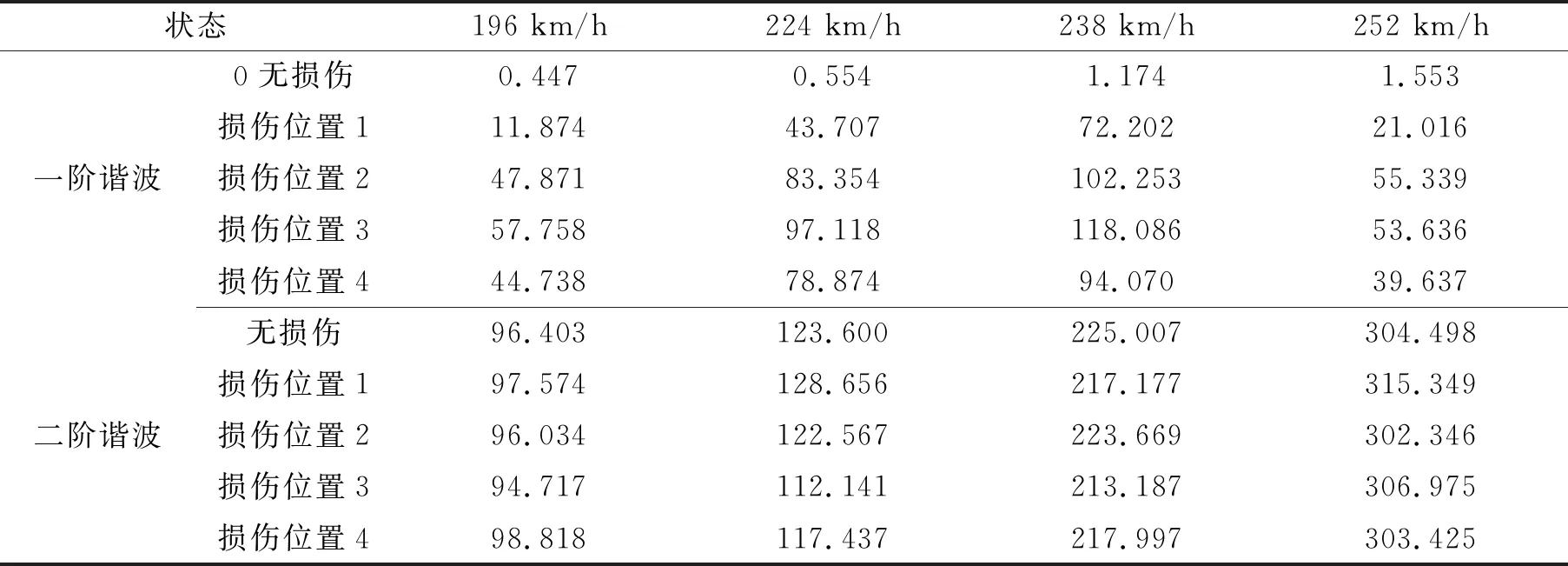
表7 不同损伤位置下旋转面侧向载荷的各阶谐波量
由图11可知,柔性梁损伤位置靠近桨毂中心时,其尾桨中心升力方向载荷的一阶谐波量逐渐增大。由图12可知,尾桨中心升力载荷的二阶谐波量主要与飞行速度正相关,而与损伤位置相关性较弱,随着损伤位置远离尾桨毂中心,其二阶谐波有微小下降趋势。
由图13可知,旋转面内侧向载荷的一阶谐波量与损伤位置有一定的相关性,当损伤位置靠近支撑轴承位置时,其一阶谐波量增大。由图14可知,旋转面内侧向载荷的二阶谐波量主要与飞行速度呈正相关,而与损伤位置的相关性较弱。
3 结论
通过对无轴承尾桨柔性梁损伤对尾桨振动载荷的影响分析后,可以得出以下几个结论:
1)随着无轴承尾桨柔性梁损伤程度增大,尾桨中心升力方向载荷和旋转面内侧向载荷的一阶谐波逐渐增大;
2)尾桨中心升力方向载荷和旋转面内侧向载荷的二阶谐波主要与飞行速度有关,尾桨中心升力方向载荷的二阶谐波随着柔性梁损伤程度增大而增大,而旋转面内侧向载荷的二阶谐波与柔性梁损伤程度的相关性较弱;
3)柔性梁损伤位置与尾桨中心升力方向和旋转面内侧向载荷的一阶谐波有关,损伤位置靠近桨毂中心时,其尾桨中心升力载荷增大;损伤位置靠近支撑轴承时,尾桨中心旋转面内侧向载荷逐渐增大;
4)柔性梁损伤位置对尾桨中心升力方向载荷和旋转面内侧向载荷的二阶谐波敏感性都较弱。
