操纵量对旋翼气动噪声的影响规律研究

李 腾, 曹亚雄, 李志彬，樊 枫

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机独特的垂直起降、空中悬停、回转及超低空飞行能力，使其在军事、民用领域均具有广泛的用途，尤其在应对突发事件方面，更具有不可替代的作用。但是旋翼噪声大的缺点，很大程度上限制了直升机更大范围的使用。为降低旋翼产生的气动噪声，首先需要得到旋翼旋转产生气动噪声的准确值。目前有试验测量和基于FW-H方程的数值计算两种方法可得到旋翼气动噪声。试验测量直接采用麦克风采集声信号。此方法可靠，且可与数值计算方法对比验证数值计算准确性，但周期长、费时费力。数值计算例如采用WOPWOP声预测代码计算旋翼气动噪声，需要提供旋翼表面的气动载荷以及旋翼操纵量作为输入。旋翼表面的气动载荷可通过风洞试验测量或CFD(Computational Fluid Dynamics)计算得到。Visintainer把模型旋翼在DNW中试验测得的表面压力输入到WOPWOP程序中预测噪声，包括预测BVI噪声。Hassan使用全位势代码预测旋翼在BVI状态下的气动载荷，并输入到WOPWOP中，噪声计算结果与试验测得的噪声值吻合一致。Kenneth介绍了桨叶运动及桨叶载荷简化与否、总距、周期变距、预锥角和周期挥舞对旋翼声预测的敏感性分析。操纵量变化对旋翼气动噪声大小及指向性的影响规律需要进一步研究。

本文的主要目的是了解当试验测量或者数值计算旋翼产生的气动噪声时，旋翼操纵量对旋翼辐射噪声的影响规律。文中旋翼气动力采用Camrad II的自由尾迹模型进行计算；操纵状态下旋翼产生的噪声采用基于Farassat 1A方程进行气动噪声求解。采用2 m模型旋翼计算，针对斜下降典型桨涡干扰状态，分析旋翼的不同操纵量对噪声辐射的敏感性。

1 计算方法和模型

1.1 气动力计算模型

如引言所述，文中采用Johnson创建的基于自由尾迹的Camrad II平台进行旋翼的气动计算。在自由尾迹方法中使用Weissinger-L模型，如图1所示。此模型很好地结合了升力面方法和一阶升力线的优点，也称二阶升力线方法。将尾迹分解为近尾迹和远尾迹分别处理。近尾迹区域充分考虑附着涡和尾随涡的影响，附着涡分布在网格四分之一弦线上，控制点分布在3/4弦线中点。附着涡环量径向变化引起尾随涡从桨叶后缘拖出，设置涡龄角为30°后形成近尾迹。远尾迹区域主要由自由运动的卷起桨尖涡来模拟，考虑桨尖涡诱导作用，涡元诱导速度由Biot-Savart(B-S)定律确定，如式(1)所示。考虑到桨尖涡附近诱导速度计算存在奇异性，采用涡核模型对桨尖涡进行模拟，如式(2)所示。

图1 桨叶Weissing-L升力面示意图

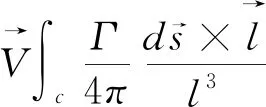
(1)

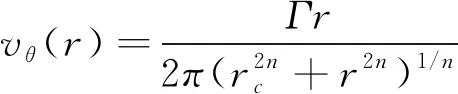
(2)

式中，为计算点至涡中心的距离，为涡核半径。涡核半径定义为最大切向速度出现的位置。

1.2 噪声计算模型

在旋翼气动噪声计算方面，Ffowcs Williams-Hawkings在Lighthill方程的基础上运用广义函数理论创建了固体边界气动发声的FW-H方程。当旋翼桨尖马赫数为亚音速时，四极子噪声对总噪声的贡献很小，可以忽略不计。FW-H方程忽略四极子噪声项后使用最广泛的形式是Farassat推导出的积分形式的F1A公式，如下所示：

(,)=(,)+(，)

(3)

式中,(，) 为总声压,(，)是厚度噪声声压，(，)为载荷噪声声压，二者的表达式分别为：

(4)

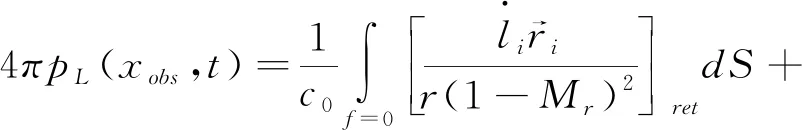
(5)

2 方法验证

为检验本文噪声计算方法对直升机旋翼前飞状态气动噪声的计算能力，选取AH-1/OLS模型旋翼作为验证算例。Schmitz等人测量了AH-1/OLS模型旋翼多个状态下的噪声数据，选取“10014状态”进行噪声计算来验证文中建立的计算方法。OLS旋翼是AH-1直升机旋翼的 1/7 缩比模型。旋翼的参数为：2片桨叶， BHT-540对称翼型，直径1.916 m，弦长0.104 m，展弦比9.22，桨叶根切比18.2%，-10°的线性扭转。桨盘倾角为1°，旋翼流场中存在明显的桨-涡干扰(BVI)现象。AH-1G/OLS模型旋翼如图2所示。

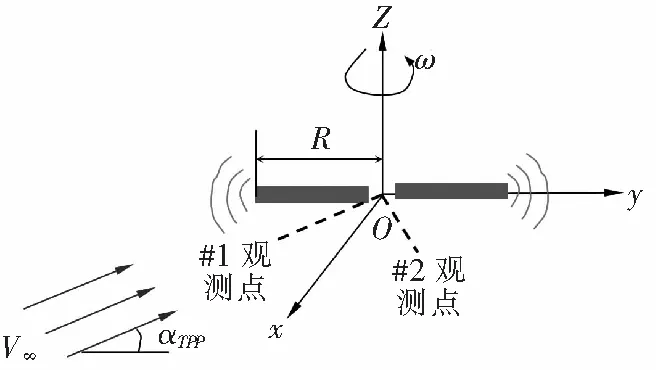
图2 AH-1G/OLS模型旋翼示意图

从图3中可以看出，本文方法在相位和幅值上均能较为准确地计算出AH-1/OLS旋翼在该状态下45°方位角左右的声压正峰值，这也正是桨-涡干扰状态的典型特征，表明了本文所建立的方法具有计算旋翼桨-涡干扰状态气动性能和噪声特性的能力。

图3 AH-1G/OLS旋翼在典型桨-涡干扰状态下的噪声计算对比

3 操纵量对旋翼噪声敏感性分析

3.1 计算模型

采用2 m模型旋翼，旋翼几何信息如表1所示。

表1 模型桨叶几何信息

悬停状态桨盘一周同一俯仰角对应的各个方位角处观测点的声压级都相同，所以结果处理只选择某一方位角处不同俯角处观测点的声压级即可。文中观测点位于0°方位角处，俯角以10°增加，具体编号如图4所示。悬停按照机身重量133 kg配平，配平变量为“向力”和“总距”，配平后锥度角=197°，总距为=964°，设此状态为基准状态。基准状态下各个观测点声压级噪声如图5所示。图中可知#3观测点声压级最高。根据旋翼产生的不同成分噪声的传播方向，选择#1，#3，#5观测点。保证桨叶气动载荷计算准确的前提下，分析旋翼各操纵量变化对旋翼噪声的影响。

图4 观测点位置

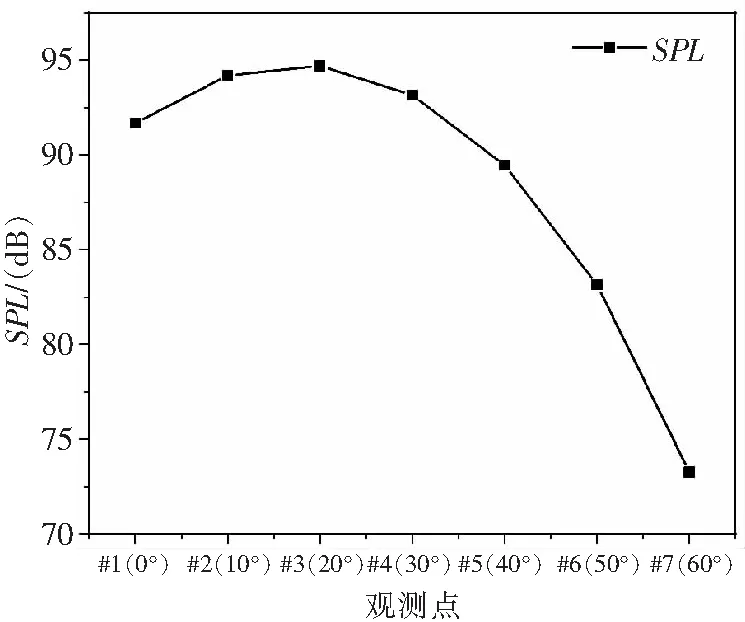
图5 基准状态下各观测点声压级

3.2 悬停状态参数影响分析

3.2.1 锥度角影响

图6和表2给出了悬停状态下锥度角变化对旋翼噪声的影响。锥度角的变化为=0°、1°、1.97°、3°、4°，Δ=-1.97°、Δ=-1.97°、-0.97°、0°、1.03°、2.03°。可以看出锥度角变化对各观测点厚度噪声几乎没有影响，这与已知厚度噪声仅由旋翼几何特性决定的结论相吻合。锥度角变化对桨盘平面内观测点处(#1)载荷噪声的影响要大于对桨盘下方观测点处(#3、#5)载荷噪声的影响。因此，需要考虑锥度角变化对桨盘平面内观测点噪声的影响；对桨盘平面下方其他观测点而言可以忽略锥度角对噪声的影响。

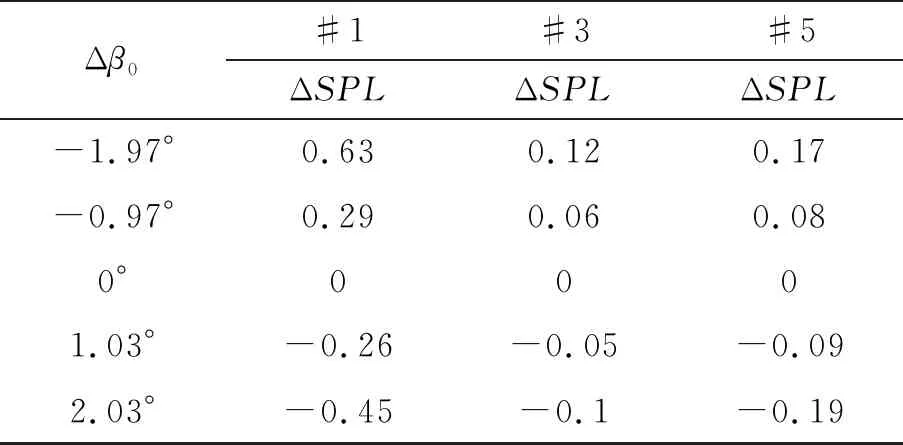
表2 锥度角变化对各观测点声压级的影响

图6 悬停状态锥度角影响

3.2.2 总距角影响

图7和表3给出了悬停状态下，旋翼总距角变化对3个观测点处声压级的影响。=7.5°、8.5°、9.64°、10.5°、11.5°，定义Δ=-9.64°，Δ=-2.14°、-1.14°、0°、0.86°、1.86°。同样可以看出总距变化对各观测点厚度噪声几乎没有影响，仅对载荷噪声产生影响。总距角增大，各个观测点处载荷噪声均增大。

表3 总距变化对各观测点处声压级的影响

图7 悬停状态总距变化对各观测点噪声的影响

3.3 前飞状态参数影响分析

前进比=0.15，配平后旋翼的操纵量如表4所示。图8为前飞状态下旋翼的声辐射球，设此状态为基准状态。

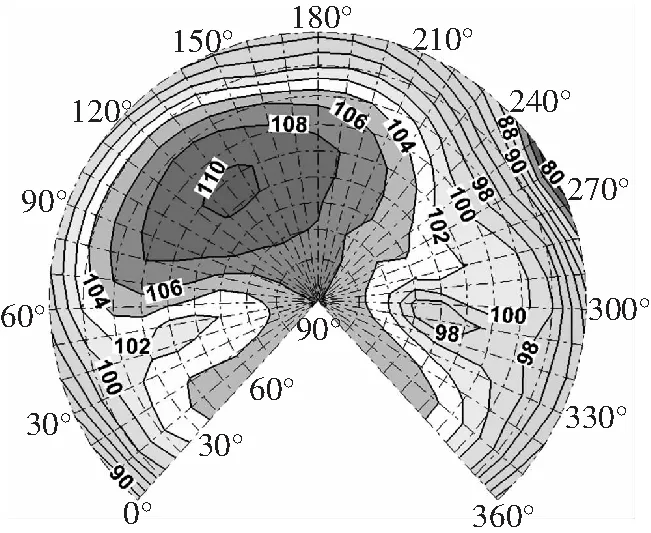
图8 前飞基准状态声辐射球

表4 前飞基准状态旋翼配平后的操纵量

3.3.1 轴倾角的影响

采用单一变量法，保证其他参数不变，改变轴倾角。=-1°，-2°，-3°,Δ=-(-253°),故Δ=153°,053°,-148°。图9为不同轴倾角状态下对应的声辐射球。图9(a)中可以看出轴倾角增量为1.53°时，10°方位角桨盘平面声压级减小2.4 dB； 方位角160°处桨盘平面内及下方5°范围内噪声减小1.8 dB；而150°～180°方位角，桨盘下方10°范围内噪声增大1.4 dB。对比图9(a)、(b)、(c)可知，前飞时，轴倾角的变化会影响10°方位角和桨盘前方观测区域处的噪声，轴倾角前倾越大，噪声差值越大，轴倾角变化小时(0.5°)，可忽略轴倾角的影响。

图9 前飞状态轴倾角的影响

3.3.2 锥度角的影响

其他参数不变，锥度角的变化为=1°,2°，Δ=-045°,055°。图10(a)中250°方位角处桨盘平面内噪声增大0.9 dB，而270°方位角处噪声减小0.3 dB。对比图10(a)、(b)两图可发现，锥度角减小或增大后，对应的噪声增大和减小区域刚好对调。锥度角的变化较小时，对观测点噪声的影响不明显，可忽略锥度角的影响。

图10 前飞状态锥度角的影响

3.3.3 后倒角和侧倒角的影响

图11为1和1同时为0°和2°旋翼的声辐射球，以此来分析后倒和侧倒的影响。图11(a)可以看出后倒和侧倒角变化较小(1=1=0°)时，260°方位角处桨盘平面内噪声增大0.7 dB，其他观测点噪声影响不大，可以忽略对旋翼噪声的影响；图11(b)中当后倒和侧倒角变化较大时(1=1=2°)，方位角240°～300°范围内噪声增大1 dB，最大值可达4 dB，其他区域噪声噪声影响不大。所以，后倒角和侧倒角变化小时，可以忽略其影响。

图11 前飞状态下后倒角和侧倒角的影响

3.3.4 周期变距的影响

其他参数不变，横向周期变距的变化为=-1°，-3°,Δ=077°,-123°。对比图12(a)、(b)可发现，横向周期变距增大或者减小，声辐射球噪声降低区域和增大区域正好对调；横向周期变距变化，影响的是20°～50°方位角、240°附近和270°附近观测点的噪声。对比图8基准状态可知，横向周期变距的变化对噪声指向性无影响。

图12 前飞状态横向周期变距的影响

图13为纵向周期变距变化后旋翼产生噪声的变化。=1°,3°,4°，Δ=-127°,073°173°。可以看出，纵向周期变距影响的是桨盘后方0°～30°方位角、桨盘前下方150°～180°方位角和210°～330°后行侧范围靠近桨盘平面的区域，且纵向周期变距变化幅值增大，噪声变化幅值增大，影响越大，但对噪声指向性并不构成影响。

图13 前飞状态纵向周期变距的影响

3.4 斜下降参数影响分析

接着分析斜下降状态操纵量对旋翼噪声的影响。轨迹角为-6°，前进比0.15，配平后旋翼的操纵量如表5所示。图14为前飞状态下旋翼的声辐射球，设为基准状态。

表5 斜下降状态配平后旋翼的操纵量

图14 斜下降基准状态声辐射球

3.4.1 轴倾角的影响

其他参数不变，轴倾角变化为=-1°,-3°，Δ=092°,-108°。图15中可以看出斜下降状态轴倾角变化对旋翼噪声的影响同前飞状态下轴倾角变化对旋翼噪声的影响相似。轴前倾越大(=-108°)，旋翼前下方10°～20°俯角范围噪声降低1 dB，桨盘下方5°范围内噪声增大1.2 dB；桨盘20°方位角后方增加1.2 dB。轴前倾角相对基准状态变小(=092°)，噪声变化区域正好对调。轴倾角变化1°幅值左右，对噪声的影响大约为1 dB。

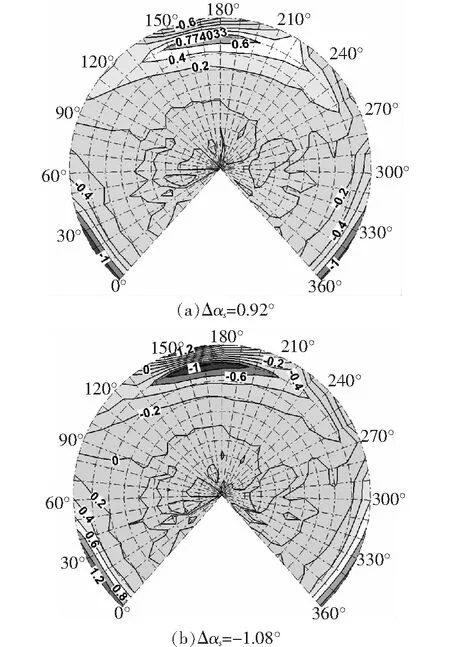
图15 斜下降状态轴倾角的影响

3.4.2 锥度角的影响

其他参数不变，锥度角的变化为=1°,2°，Δ=-03575°,06425°。图16斜下降情况下锥度角的影响同前飞状态相似。锥度角变化会影响250°和270°方位角附近观测点的噪声，但对噪声指向性并不构成影响。

图16 斜下降状态锥度角的影响

343 后倒角和侧倒角的影响

同样设置1和1同时为0°和2°，分析后倒和侧倒的影响，如图17所示。忽略后倒侧倒(1=1=0°)，260°方位角、桨盘下方15°观测点附近，噪声降低0.6 dB，270°方位角噪声增大1.2 dB；后倒角和侧倒角增大，后行侧240°～310°范围内噪声增大1 dB以上。因此，后倒角和侧倒角变化小时，可以忽略影响。

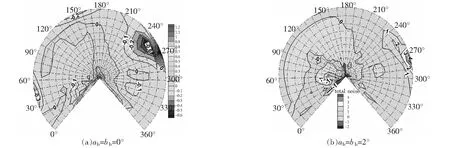
图17 斜下降状态后倒角和侧倒角的影响

3.4.4 周期变距的影响

其他参数不变，横向周期变距的变化为=-1°,-3°,Δ=087°,-113°。对比图18(a)、(b)可发现，横向周期增大和减小，声辐射球噪声降低区域和增大区域正好对调；横向周期变距变化，影响的是前行侧20°～150°方位角、250°附近和280°附近后行侧观测点的噪声。对比图14基准状态可知，横向周期变距的变化对噪声指向性无影响。

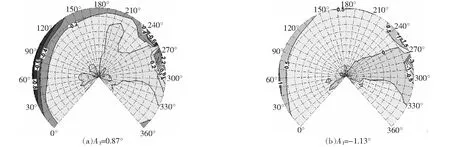
图18 斜下降状态横向周期变距的影响

其他参数不变，纵向周期变距的变化为=05°,1°,3°,4°，Δ=-125°,-074°,126°,226°。从图19可以看出纵向周期变距影响的是桨盘后方0°～40°方位角、桨盘前下方150°～180°方位角和260°～360°后行侧范围靠近桨盘平面的区域，且纵向周期变距变化幅值增大，噪声变化幅值增大，影响增大，但对噪声指向性并不构成影响。

图19 斜下降状态纵向周期变距的影响

3.5 爬升参数影响分析

爬升状态，配平后旋翼的操纵量如表6所示。图 20为爬升状态下旋翼的声辐射球，设为基准状态。

表6 爬升状态配平后旋翼的操纵量

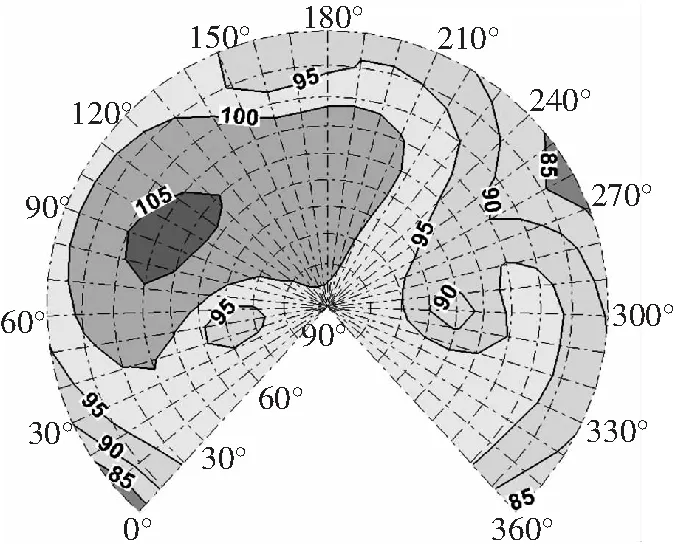
图20 爬升状态基准状态下的声辐射球

351 轴倾角的影响

其他参数不变，轴倾角变化为--1°,-3°，Δ=129°,-171°。轴前倾增大(=-171°)，旋翼前下方噪声降低0.6 dB，后方增加1 dB。轴前倾角相对基准状态变小(=129°)，噪声变化区域正好对调，旋翼前下方噪声增大1.2 dB，正后方噪声减小2.2 dB。

3.5.2 锥度角的影响

其他参数不变，锥度角的变化为=05°,25°,Δ=-10141°,09859° 。图22爬升情况下锥度角的影响同前飞状态相似。锥度角变化会影响10°和240°方位角附近观测点的噪声，但对噪声指向性并不构成影响。

3.5.3 后倒角和侧倒角的影响

设置1和1同时为0°和2°，分析后倒和侧倒的影响，如图23所示。忽略后倒、侧倒(1=1=0°)，260°方位角、桨盘下方10°观测点附近，噪声增大0.9 dB，20°方位角噪声减小0.4 dB；后倒角和侧倒角增大(1=1=2°)，后行侧240°～270°范围内噪声减小1 dB以上，10°～50°方位角噪声增加1 dB以上，270°下方20°方位角附近噪声增大1.5 dB。所以后倒角和侧倒角变化小时，可以忽略其影响。

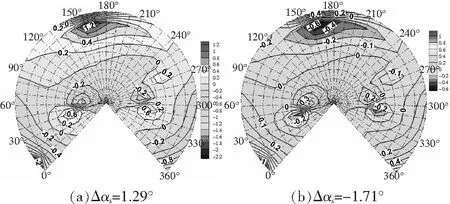
图21 爬升状态轴倾角的影响

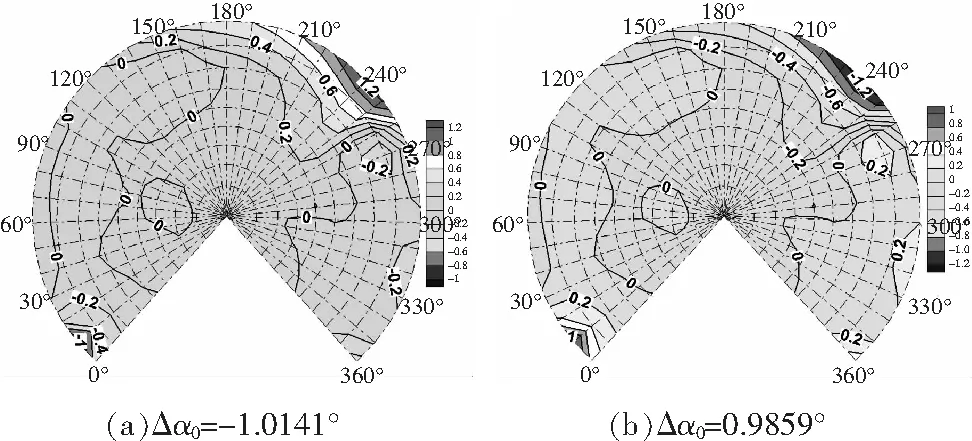
图22 爬升状态锥度角的影响

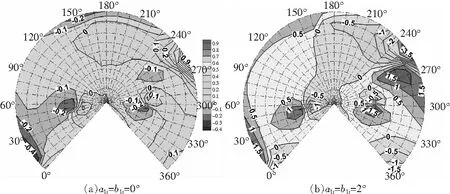
图23 爬升状态后倒角和侧倒角的影响

3.5.4 周期变距的影响

其他参数不变，横向周期变距的变化为=-05°,-2°，-3°Δ=089°,-061,-061°。同样对比图24(a)、(b)、(c)可发现，横向周期增大或减小，声辐射球噪声降低区域和增大区域正好对调；横向周期变距变化，影响的是0°～30°方位角、260°附近观测点的噪声，且周期变化幅值相对于基准值增大，噪声影响区域扩大。对比图20基准状态可知，横向周期变距的变化对噪声指向性无影响。

图24 爬升状态横向周期变距的影响

其他参数不变，纵向周期变距的变化为=1°,2°,3°,4°，Δ=-141°,-041°,059°,159°。可以看出纵向周期变距影响的是桨盘后方0°～60°方位角、桨盘前下方150°～180°方位角和210°～330°后行侧范围靠近桨盘平面的区域，且纵向周期变距变化幅值增大，噪声变化幅值增大，影响增大，但对噪声指向性并不构成影响。

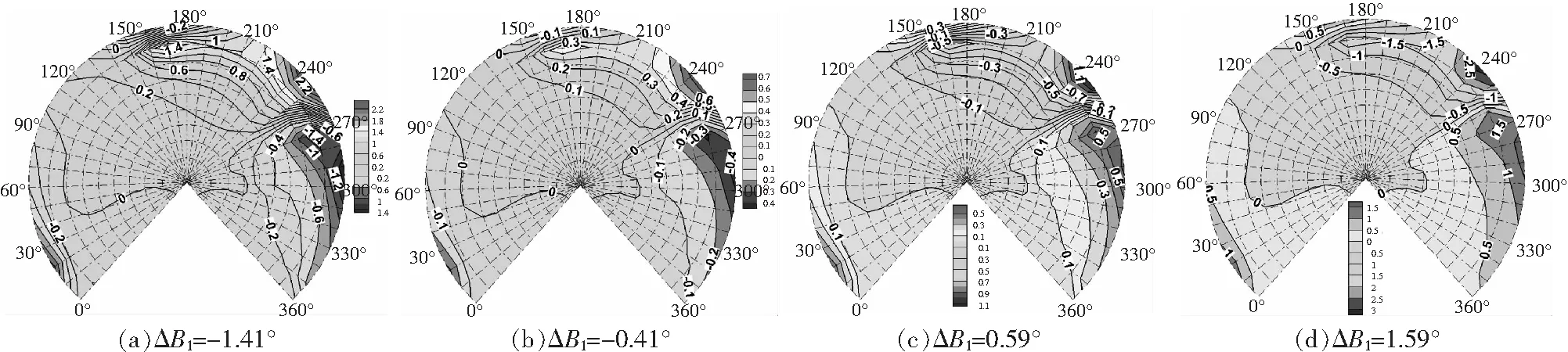
图25 爬升状态纵向周期变距的影响

4 结论

本文基于自由尾迹模型和Farassat 1A方程对旋翼在不同操纵量下的噪声进行计算研究，得出的结论如下：

1)悬停时，锥度角变化对桨盘平面内观测点处载荷噪声的影响最大，只需考虑其变化对桨盘平面内观测点噪声的影响，忽略对桨盘平面下方的影响；总距角增大，对所有观测点处载荷噪声和厚度噪声的影响均增大，但变化量小时增量并不大。

2)前飞时、斜下降和爬升状态下，各操纵量变化对旋翼噪声的影响规律相似。操纵量的改变不会对噪声指向性产生影响。

3)轴倾角的变化会影响桨盘后方和桨盘前方方位角处下方20°范围内观测区域的噪声，且轴倾角前倾越大，对噪声的影响越大，轴倾角变化小于0.5°，可忽略轴倾角的影响；锥度角的影响可忽略不计。

4)挥舞一阶对噪声的影响也集中在桨盘平面附近，变化较小时同样可忽略其影响；一阶周期变距影响后行侧，且变化越大，影响范围越广，噪声变化值越大。