逆向思维在中学数学几何教学中的价值分析

胡小红

摘 要：逆向思维和常规思维具有较大的差异性，它是突破定性思维、超越传统理论的思维模式。在初中数学几何教学中，合理应用逆向思维能够打开新的教学领域，形成新的教学思维模式。在教学过程中，通过加强学生的逆向思维训练和意识，不仅能使学生的思维能力更加活跃，还可以提高学生的创新意识。

关键词：逆向思维;中学几何;价值分析

【中图分类号】G633.6            【文献标识码】A             【文章编号】1005-8877（2022）03-0038-04

An Analysis of the Value of Reverse Thinking in the Teaching of Geometry of Mathematics in High Schools

HU Xiaohong  （Fucheng Junior High School， Kangle County， Linxia Prefecture， Gansu Province， China）

【Abstract】Reverse thinking and conventional thinking are quite different. It is a thinking mode that breaks through qualitative thinking and transcends traditional theories. In the teaching of mathematics and geometry in junior high schools， the rational application of reverse thinking can open up new teaching areas and form new teaching thinking modes. In the teaching process， by strengthening the students' reverse thinking training and awareness， not only can the students' thinking ability be more active， but also the students' sense of innovation can be improved.

【Keywords】Reverse thinking; High school geometry; Value analysis

初中数学是奠定学生数学基础的重要阶段，能够使学生获得较强的数学预算能力和思维逻辑能力，尤其是几何教学，能够有效提高学生的空间想象能力。在几何教学过程中，需要合理应用逆向思维教学方式，有效培养学生的思维推理能力和分析能力。

1.利用逆向思维，进行几何定义教学

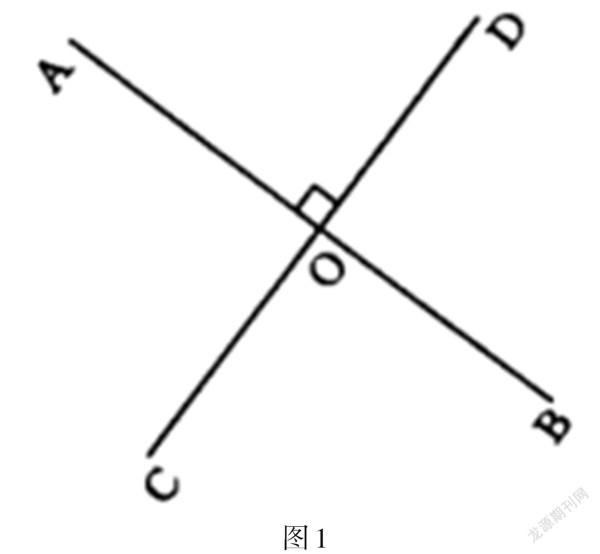
在初中几何教学中，会学习到大量的几何定义，在几何定义教学过程中时，可以应用逆向思维教学方式进行教学，以此来强化学生的逆向思维。比如，在对人教版初一数学七年级下册《垂线》教学时，需要学生理解垂线、垂线段的概念，并会利用三角尺或者量角器过一点画已知直线的垂线。垂线的定义为当两条直线相交的四个角中，有一个角是直角时，那么这两条直线是相互垂直的，其中一条直线是另外一条直线的垂线，两条直线的相交点叫作垂足。而应用逆向思维也可以推理出，如果这两条直线是相互垂直的，那么四个角都为直角。

如图1所示，如果直线AB、CD在O点出相交，且∠AOD为直角，或者其他三个角任意一个角为直角，那么AB⊥CD;应用逆向思维推理，如果直线AB和CD互相垂直，垂足为O，那么四个角都为直角，即∠AOC=∠AOD=∠COB=∠BOD=90°，根据以上推理，利用几何符号可以列出详细运算步骤。

正向推理过程：

[∵∠AOD=90°]（已知）

[∴AB⊥CD]（垂直定义）

逆向推理过程：

[∵AB⊥CD]（已知）

[∴∠AOC=∠AOD=∠COB=∠BOD=90°]（垂直定義）

除了使用∠AOD论证垂直定义以外，还可以使用其他三个角的任意一角进行正向思维推理和逆向思维推理，通过学生反复练习推理，能够使学生较为轻松的理解垂直定义，并且能够灵活应用垂直定义。另外，在“余角”定义教学过程中，教师需要使学生从正向和逆向两个方面充分理解并掌握定义。比如，从正向思维理解定义：如果α+β=90°，那么α和β互为余角;从逆向思维理解定义：如果α和β互为余角，那么α+β=90°。在“余角”教学过程中，需要教师详细讲解“互为余角”的含义，如α和[β]互为余角，那么α是[β]的余角，从逆向思维来说，[β]也是α的余角。另外，“互余”是以两个角为基础，既不是一个角，也不是两个以上的角，而且两个角之间不存在位置关系，只存在数量关系。因此，从逆向思维学习几何定义，不仅能够使学生较为深刻理解“余角”定义，还能使学生在几何学习过程中灵活应用“余角”定义。

2.利用逆向思维，强化几何证明教学

在人教版初中几何教学过程中，几何证明是较为重要的题型，由于年级的不同，几何证明题的形式和难易程度也在一定范围内存在差异性。在对七年级进行几何证明教学时，教师需要将几何定义的基本定理和应用作为教学重点，从难易程度上来说，相对比较简单。在对八年级进行几何证明教学时，题型难度明显增强，而且知识面也更为宽广，如在对三角形全等进行证明过程中，需要运用到较多的几何定义，有可能应用到轴对称基本定理，并对轴对称定理进行巩固得到更深一层的定理知识，也有可能应用到四边形几何基本定义，并对其进行拓展，从而得到相关线条是否相等，是否有倍分关系，或者相关角是否相等，是否有倍分关系。

在对九年级进行几何证明教学时，知识重点和难易程度都得到了全面提升，需要将七年级和八年级的几何知识进行有效整合，使学生全方面掌握几何重点知识，并且能够在练题过程中灵活应用。为了使学生更好地学习几何证明，针对各个年级的学习情况，可以将逆向思维模式融入具体教学过程中。比如，如图2所示，准备一张长方形纸片，将其四个角依次标注为A、B、C、D，将长方形沿AC线对折，此时△ACD会翻至△ACD’，而且AD’和BC相交于E点，对△AEC的形状做出准确判断，并列出详细判断步骤。

在判断三角形具体形状之前，需要充分了解三角形的基本知识，按照角的大小分类，可以分为锐角三角形、直角三角形和钝角三角形三种类型;按照边关系的分类，可以分为等腰三角形和等边三角形;将直角三角形和等腰三角形结合，可以得到等腰直角三角形。根据以上三角形的基本理论知识，可以对△AEC进行逆向思维假设论证，由于锐角三角形和钝角三角形没有特殊性，因此，可以将直角三角形、等腰三角形、等腰直角三角形或者等边三角形进行主要逆向思维证明。如果将△AEC看作等腰三角形，根据等腰三角形的基本定理只需证明∠EAC=∠ECA。由于△ACD’是由△ACD翻折得来，两个三角形的形状、大小具有一致性，因此∠DAC=∠EAC;同时，根据长方形ABCD的基本定义可知对边平行，所以AD∥BC，也可得出∠DAC=∠ACE，此时可知，∠EAC=∠ACE，根据等腰三角形的基本定义可知△AEC为等腰三角形。如果将△AEC看作直角等腰三角形，∠AEC是∠ABE和∠BAE之和，而∠ABE=90°，可知∠AEC≠90°，因此，△AEC不可能是等腰直角三角形。另外，通过以上条件也可以得出，△AEC也不可能是等边三角形。通过逆向思维分析，可以得出正确的几何证明解题思路，按照思路列出详细步骤，因此，也可得出正确的证明解题过程。详细证明过程如下：

证明：∵长方形ACDE的对边AD∥BC

∴∠DAC=∠ECA

∵△ACD=△ACD’

∴∠DAC=∠EAC

∴∠ECA=∠EAC

∴△AEC为等腰三角形

在证明过程中，需要列出重要的证明步骤，不需列出逆向思维思考步骤。但是教师通过逆向思维进行几何证明教学，能使学生快速找到解题思路，从而强化学生的几何证明练习。

3.利用逆向思维，正确引导学生思考

在初中几何教学过程中，教师可以利用逆向思维引导学生进行几何知识总结，从而使学生发现几何知识的互逆性。比如，在人教版七年级下册“平行线”教学过程中，课本上平行线的定义为永远不会相交的两条直线可称为平行线。如果教师只是将平行线的定义讲述给学生听，学生无法深刻理解平行线定义，也无法在脑海中形成较为直观的理解画面。教师利用逆向思维进行平行线教学，让学生思考平面内直线的位置关系都有哪些，在思考的过程中，不仅能够锻炼学生的思维能力，使之更加活跃，还能提高学生的学习兴趣。另外，教师还可以鼓励学生到讲台上对思考结果进行讲述，并在黑板上将自己思考的平面内直线的位置关系画出来。学生对所画的直线进行观察，有些直线是会相交于某点，有些直线则是不会相交，通过逆向思维教学使直观的画面呈现在黑板上，可以使学生更深刻地理解平行线概念。学生在学习平行线几何知识的过程中，无法有效区分平行线的判定和性质，教师需要将平行线的判定和性质作为重点教学内容，使学生充分理解判定定理和性质定理，并对其进行充分比较。在对判定定理和性质定理进行比较的过程中，不难发现两者存在互逆性，即判定定理的条件是性质定理的结论，而判定定理的结论是性质定理的条件，条件和结论有着相反关系，从而学生可以从本质上理解判定定理和性质定理。比如，从角的大小关系得到两条直线平行的结论，是平行线的判定;从逆向思维考虑，从两条直线平行得到角存在相等或者互补关系，是平行线的性质，如图3所示。

可得出平行线的判定：如果[∠1=∠2]那么[AB∥CD];如果[∠2=∠3]，那么[AB∥CD];如果[∠2+∠4=180°]，那么[AB∥CD];也可得出平行线的性质：如果[AB∥CD]，那么[∠1=∠2=∠3];如果[AB∥CD]，那么[∠2+∠4=180°]。

4.利用逆向思维，加强几何反面例题训练

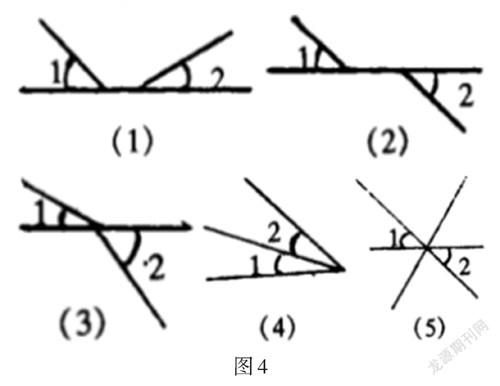
教师在应用逆向思维进行几何教学过程中，不仅需要利用正面例题进行几何教学，还需要利用反面例题进行几何教学，并使正反例题教学进行有效整合，形成独具特色的几何教学模式。传统的教学模式通常是应用正面例题教学模式，这种教学模式较为枯燥，有可能降低学生对几何知识的学习兴趣，而应用反面例题的逆向思维教学模式，不仅能不断培养学生的思考力，有效激发学生对几何知识的学习兴趣，还能使学生更为深刻地理解几何知识，并在数学学习中灵活运用。比如，在人教版七年级数学“对顶角”教学过程中，可以对学生加强思维训练，反复进行几何反面例题训练，让学生深刻理解对顶角的含义。如图4所示：如何判断∠1和∠2是对顶角？

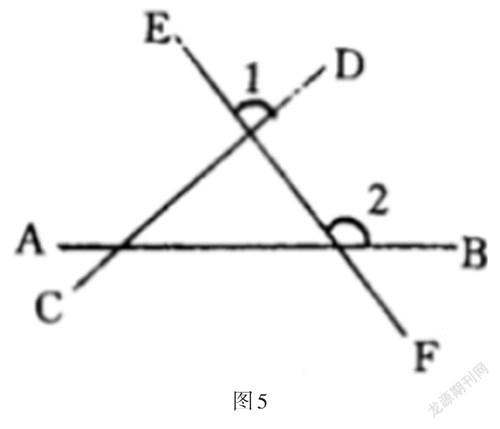
在几何学中，对顶角是两个角之间的一种位置关系。两条直线相交时会产生一个交点，并产生以这个交点为顶点的四个角，称其中不相邻的两个角互为对顶角。或者说，其中的一个角是另一个的对顶角。通过逆向思维可得出，只有图4（5）的∠1和∠2是对顶角，两个角是两条直线相交而构成的角，同时有共同的定点，没有共同边。又比如，在平行线性质定理进行教学时，教师会对同位角进行讲解，如果两直线平行，那么同位角相等。而学生在几何学习过程中，经常会忽略已知条件，认为只要两个角存在同位角的关系，那么这两个角就是相等的。教师可以通过反问的形式对学生进行提问，如果兩个角是同位角关系，那么两个角的大小是否相等？部分学生会回答相等，部分学生会回答需要根据情况而定。教师可以在黑板上画出图形（见图5），两条直线AB、CD被直线EF所截，图上的∠1和∠2是否存在同位角关系，直线AB和CD是否存在平行关系？

学生观察图形可以得出，两个角是同位角，但是直线AB和CD不存在平行关系，因此，∠1≠∠2。通过反面例题可知，同位角相对是平行线特有的性质，但不是所有同位角都具有相等的关系，只有在两条直线存在平行关系的条件下，同位角才具有相等的特性。

5.利用逆向思维，强化正反逻辑推理

教师在应用逆向思维进行几何教学过程中，需要有效培养学生的发散性思维能力，可以将正反逻辑推理的教学方法融入日常教学过程中，使逆向思维和正反逻辑推理能够形成相辅相承的特色几何教学模式，从而有效提高几何教学效率。比如，在人教版几何教学过程中，需要论证一个三角形中至少有一个角是小于或者等于60°，教师可以通过正反逻辑推理的方式进行论证，假设这个三角形的三个角都大于60°，论证这个三角形是否存在。而根据三角形的基本定理可知，三角形的三个内角之和为180°，如果三个角都大于60°，那么之和也大于180°，与三角形的基本定理相违背，因此，可得出这个三角形不存在。通过逆向思维和正反逻辑推理结合，可得出一个三角形中只有一个角是小于或者等于60°的结论是正确的。

6.结语

综上所述，逆向思维教学模式是初中几何教学的重要教学部分，通过逆向思维教学，可以有效提高学生的学习兴趣，使学生开动脑筋，培养学生的思考能力和发散思维能力，从而使学生得到全面发展。

参考文献

[1]王国森.初中数学教学中学生逆向思维的培养策略[J].知识窗（教师版），2021（08）.

[2]张前进.初中数学教学中学生逆向思维能力的培养分析[J].文理导航（中旬），2021（09）.

[3]冯丹.浅谈逆向思维在中学数学几何教学中的作用[J].考试周刊，2020（22）.

[4]赵陆英.初中平面几何中逆向思维培养的教学研究[D].华中师范大学，2019.

[5]郑烈平.在平面几何教学中促进学生逆向思维能力[J].福建基础教育研究，2016（11）.

3597500589248