分数阶低通滤波器的优化设计研究

何 雪，胡志忠

（南京航空航天大学电子信息工程学院，江苏南京 211106）

1 引言

分数阶微积分也被称作非整数阶微积分.由于分数阶微积分的阶数不再局限于整数可为任意的复数从而可以实现连续阶微积分，因此具有更广泛的通用性，是经典的整数阶微积分理论的扩展，换句话说，整数阶导数和积分运算只是分数阶导数和积分的特例.

分数阶微积分作为一种数学理论，几个世纪之前就已经由莱布尼兹提出了，但近年来才在实际应用中被使用.如今，将分数阶微积分的理论概念引入各个学科方面的研究工作日趋活跃，分数阶微积分的应用范围已稳步扩大到工程和科学的不同领域，例如电路理论和设计［1］、控制理论［2］、电磁学［3］和机器人学［4］等.下面给出Riemann-Liouville 分数阶微分定义［5～7］.

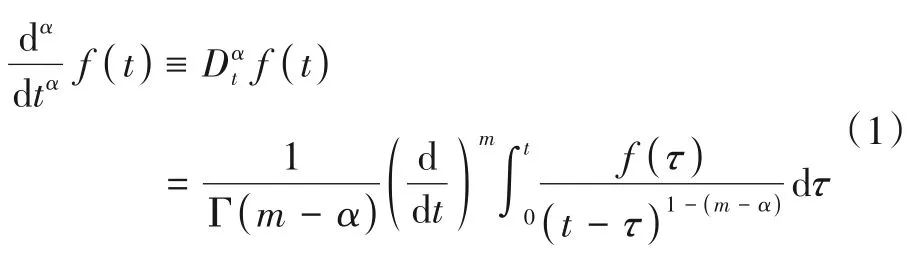
其中，m为正整数，α为实数，且m-1 ≤α＜m，Γ(·)为Gamma 函数.在零初始条件下，式（1）的拉普拉斯变换为

因此，可以定义一种阻抗与sα成比例的通用分数器件［8］，传统电路元件如电容、电阻和电感分别是该器件阶数α为-1、0 和1 时的特殊情况.传统电容器两端的电压表达式定义为流过该电容器的电流的整数次积分，可以使用非整数阶积分将电容扩展到分数域并进行拉普拉斯变换，在零初始条件下，分数阶电容的阻抗为，分数阶电容的单位为F/s1-α，简单起见，下文中统一将分数阶电容单位表示为F.在电路中使用分数阶元件可以将电路从整数阶扩展到更一般的分数阶，分数阶电容器所提供的自由度提高了设计灵活性.尽管目前市场上还没有商用的分数阶电容器出售，但分数阶电容的制造已处于研究阶段［9～11］，相信不久的将来会有商用分数阶电容的出现.在本文中，使用Foster Ⅰ型RC串并联网络模拟分数阶电容.

在传统的模拟信号处理领域，连续时间滤波器可以被归类为一阶、二阶或n阶电路，其中n是整数.因此，这些整数阶滤波器的阻带衰减特性仅可以相对于n逐步变化.例如，一阶和二阶低通滤波器只能分别产生-20 dB/十倍频和-40 dB/十倍频的滚降.如果将分数阶电容引入滤波电路中，则可以克服传统滤波器响应中的这种限制.例如，一个1+α（0 ＜α＜1）阶低通滤波器的阻带衰减为-20(1+α)dB/十倍频，也就是说，其滚降可以基于α的值介于-20 dB/十倍频和-40 dB/十倍频之间.这种滤波器被称为分数阶滤波器，它可以灵活地调整阻带衰减，也就意味着可以对过渡带的带宽进行灵活调整.此外，分数阶滤波器的指标将与分数阶电容的阶数α相关，增加了一个自由度.分数阶滤波器相对于整数阶滤波器拥有更大的设计自由度，体现在两个方面：一个方面是分数阶滤波器传递函数中拉普拉斯算子的指数可以为分数而不仅仅是整数；另一个方面是在电路实现时，分数阶电容的阻抗为1/sαc，相对于整数阶电容的阻抗1/sc多了一个关于α的设计自由度.

分数阶滤波器的一个优势应用场合是亚赫兹（180 µHz～241 mHz）滤波，而亚赫兹滤波在生物医学、信号处理、传感器［12］等领域有多种应用.例如生物医学信号通常在毫赫兹到几百赫兹的范围内，因此，需要在处理之前先使用亚赫兹滤波器来调理信号.参考文献［13］指出，用整数阶滤波器实现亚赫兹滤波，需要很大的时间常数τ才能实现较小的-3 dB 截止频率；而若用分数阶滤波器来实现亚赫兹滤波，可以基于分数阶滤波器的固有特性，仅通过更改阶数α的值就可以得到亚赫兹范围的超低截止频率.这将为低频应用领域的电路设计人员提供额外的自由度.

目前为止，国内外学者采用了多种方法来设计分数阶滤波器，这些方法既有优化方法也有非优化方法［14，15］，其中优化方法大致可以分为三类.第一类：使用一些优化技术确定分数阶滤波器对应的分数阶传递函数中的系数进而得到符合应用要求的分数阶模拟滤波器.例如Freeborn 等人［16］使用非线性最小二乘法对1+α阶的分数阶低通滤波器传递函数进行系数优化，使其逼近二阶Chebyshev 低通滤波器的通带纹波特性，从而确定给定阶数下的最优系数，完成分数阶滤波器的设计；Khanna 和Upadhyay［17］利用模拟退火算法（Simulated Annealing）易于实现且能获得组合问题最优解的特点，将其用于设计分数阶Butterworth 低通滤波器.第二类：先对分数阶滤波器的传递函数进行处理，把分数阶滤波器传递函数中的sα用其近似的有理分式替换［2］以得到整数阶传递函数，再使用优化的方法确定该整数阶传递函数的系数，最终用整数阶电路实现分数阶滤波器性能.例如Freeborn 等人［18］把1+α阶低通滤波器传递函数中的sα替换为近似的二阶有理分式后再来逼近一阶Butterworth 低通滤波器的通带最大平坦特性，得到该整数阶传递函数最优系数值完成设计.第三类：使用整数阶传递函数直接逼近分数阶滤波器传递函数的幅频响应以实现分数阶滤波器的性能.例如Mahata 等人［19］用三阶传递函数近似1+α阶理想低通Butterworth 滤波器，利用碰撞体优化（Colliding Bodies Optimisation）算法得到整数阶传递函数中的各个系数从而得到具有分数阶Butterworth 低通滤波器特性的整数阶电路.

迄今为止，大部分文献是关于分数阶Butterworth和Chebyshev 等特殊类型的滤波器的优化设计方法理论研究［14～19］，参考文献［20］中虽给出了过渡带宽、阻带衰减、通带最大可允许峰值以及-3 dB 截止频率四个设计指标来设计分数阶滤波器的方法，然而对于满足工程上常用的四个指标要求（即通带偏差δp、阻带偏差δs、通带边缘频率ωp以及阻带边缘频率ωs）的分数阶低通滤波器设计方法和设计流程却未见报道.本文针对工程应用中常用的这四个指标要求给出了满足指标要求的分数阶低通滤波器设计的数学模型，并使用Matlab优化工具箱中两个多目标优化函数Fminimax 和Fgoalattain分别对1+α阶和2β阶传递函数进行优化设计，总结使用这两种方法所优化设计的滤波器各自的特点.并在给定设计指标下，通过与整数阶滤波器的比较分析体现分数阶滤波器的优势.继而给出实例，设计出符合给定指标要求的分数阶低通滤波器，验证所提出的设计方法的可行性.

2 分数阶低通滤波器传递函数的优化设计

2.1 分数阶低通滤波器设计指标

众所周知，理想的低通滤波器是物理不可实现的，然而，如图1 所示，可以在偏离其理想性能的一定可容忍范围内进行滤波器的设计.通过控制四个设计指标以获得一定的滤波器响应，这四个设计指标δp，δs，ωp和ωs分别表示通带偏差、阻带偏差、通带边缘频率和阻带边缘频率.

图1 低通滤波器的设计式样（线性表示）

和整数阶一样，分数阶高通和带通滤波器等不同类型的滤波器可以直接从分数阶低通滤波器转换得到，因此本文只讨论分数阶低通滤波器的优化设计.

2.2 优化设计

2.2.1 建立数学模型

如图1 所示，对于满足给定指标要求的低通滤波器，其幅频响应在通带边缘频率ωp处满足

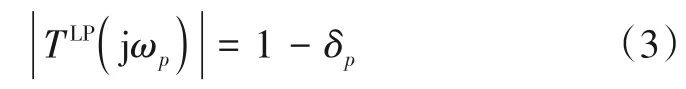
在阻带边缘频率ωs处满足

在ωmax(0 ≤ωmax≤ωp)处有

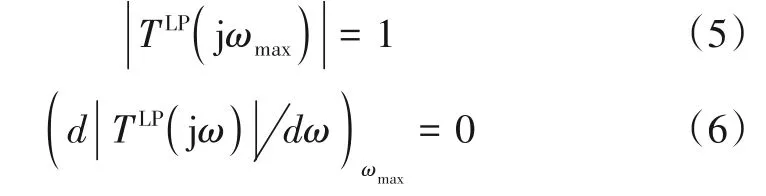
将式（3）中的“=”换为“≥”，将式（4）、式（5）中的“=”换为“≤”并保持式（6）等式不变，其幅频响应曲线仍然是满足指标要求的.下面研究两种不同传递函数的低通滤波器的参数优化.

式（7）所示为一个1+α阶低通滤波器的传递函数：

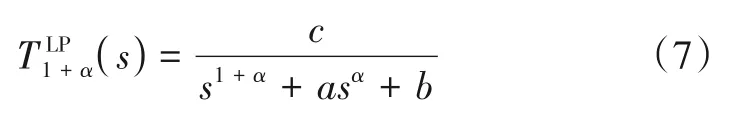
其中，a，b，c和α都是待定的参数.满足给定指标要求的低通滤波器的幅频响应在ωp，ωs和ωmax处满足式（3）～式（6），定义以下四个函数：

由此可得到相应的四个方程，显然方程中存在五个未知量，若直接解方程组可能会有无穷多解，因此本文采用优化的方法求解待定参数.本文使用Matlab 优化工具箱中的一种常见的用于求解非线性方程组的多目标优化函数Fminimax 在给定指标要求的条件下对上述问题进行优化求解，可以获得1+α 阶低通滤波器传递函数的参数最优解.

使用Fminimax优化函数时，其目标函数为

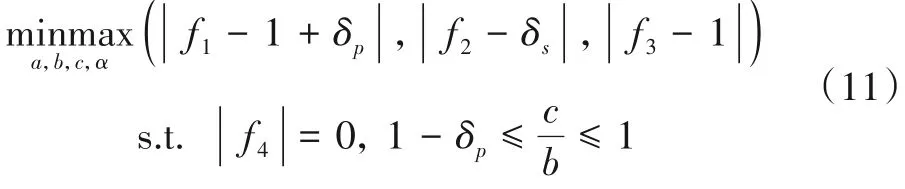
其中|f1-1+δp|，|f2-δs|和|f3-1|对应式（3）～式（5）这3 个目标；|f4|=0 为对应式（6）的约束条件，保证幅频响应曲线在ωmax处有极大值.此外，1-δp≤≤1约束条件保证了幅频响应曲线在零频率处的值介于1-δp和1 之间.未知量上下限设置为a，b，c∈[0.01，4]，α∈[0，2]，ωmax∈[0，ωp].

如前所述，满足指标要求的幅频响应曲线在ωp，ωs和ωmax处亦可满足不等式.此时，本文使用Matlab 优化工具箱中的Fgoalattain 优化函数对式（7）中的参数进行优化求解.设置goal=［δp-1，δs，1］，wi=|goali|，其目标函数为

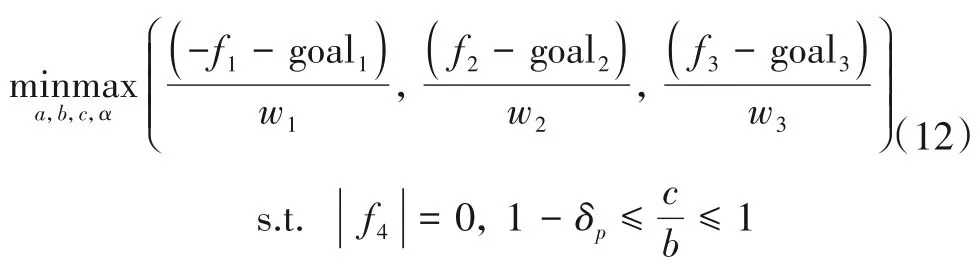
第一个优化目标中的f1前加负号保证-goal1=1-δp，第二和第三个优化目标保证fi≤goali（i=2，3）.约束条件和未知量上下限设置与Fminimax优化函数的设置一样.

如式（13）所示，2β阶低通滤波器的传递函数为

其中，k1，k2，k3和β都是待定的参数.类似于对1+α阶低通滤波器传递函数定义的四个函数，式（14）～式（16）是为2β阶低通滤波器传递函数定义的函数.

同样使用Fminimax 和Fgoalattain 优化函数在给定指标要求的条件下分别对式（13）所示的传递函数的参数进行优化求解，这两种优化函数各自所对应的目标函数与上述优化设计1+α阶低通滤波器的目标函数一样，只是将函数fi替换为gi（i=1，2，3，4），未知量上下限设置保持不变.

2.2.2 优化方法比较分析

下面通过给出3组不同的指标要求，使用Fminimax和Fgoalattain 优化函数在给定指标要求的条件下分别对1+α阶和2β阶低通滤波器传递函数的参数进行优化，得到优化后的分数阶低通滤波器传递函数并在Matlab 中进行仿真和分析，通过比较通带偏差、阻带偏差和群时延等参数，总结这两种方法所优化设计的滤波器各自的特点.

第一组：δp=0.21，δs=0.27，ωp=1.4rad/s，ωs=4.2 rad/s.对1+α阶和2β阶低通滤波器传递函数使用两种优化方法后的参数值如表1所示.

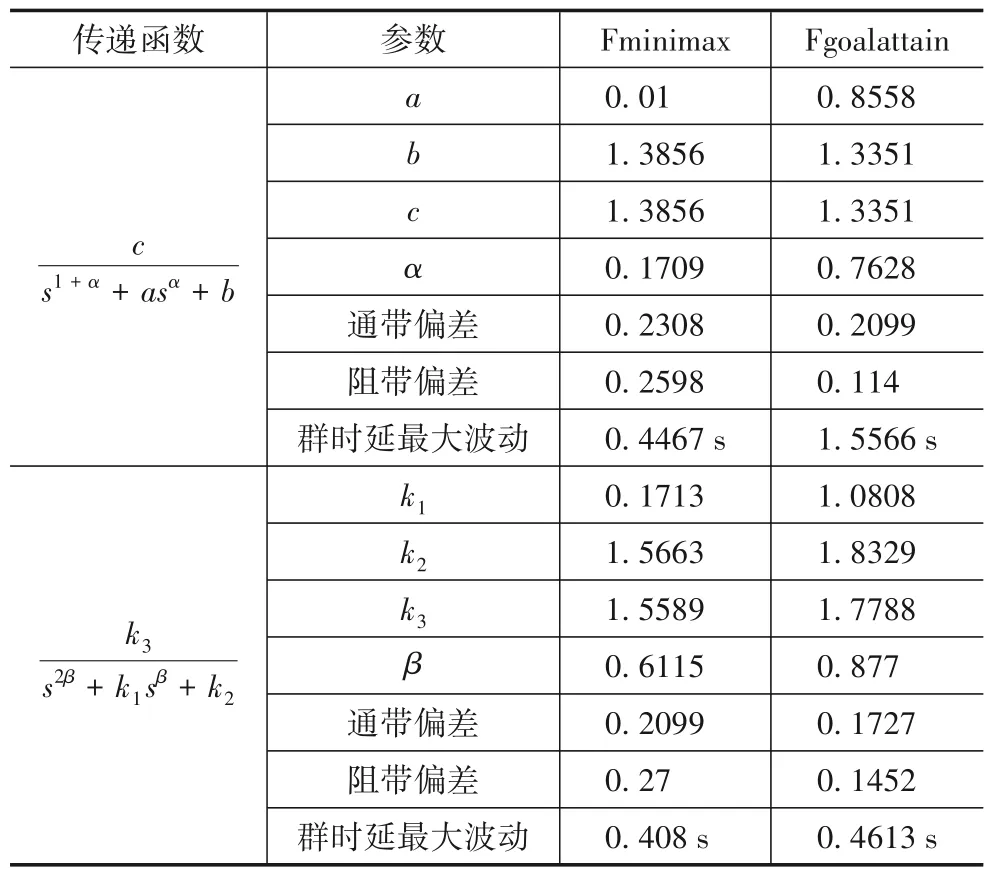
表1 第一组给定指标要求下的参数值

将优化后的参数值代入传递函数中，在Matlab 中画出它们各自的幅频响应，如图2 所示.可以看出，Fgoalattain 优化的传递函数和Fminimax 优化的传递函数通带偏差相差不大，但Fgoalattain 优化的传递函数阻带衰减远远大于Fminimax 优化的传递函数阻带衰减.

图2 第一组给定指标下的分数阶传递函数Matlab幅频响应仿真

如图3所示，虽然Fminimax和Fgoalattain分别对1+α阶和2β阶低通滤波器优化的传递函数的群时延变化范围都比较小，但相比使用Fgoalattain 优化设计的滤波器群时延，使用Fminimax 优化设计的滤波器群时延更接近一条直线.因此综合考虑，在第一组所给出的指标要求下，若希望阻带衰减尽可能大，可以使用Fgoalattain函数来优化设计低通滤波器；若希望滤波器通带尽可能平坦且通过该滤波器的信号相位失真尽可能小，可以使用Fminimax函数来优化设计低通滤波器.

第二组：δp=0.17，δs=0.29，ωp=1.8 rad/s，ωs=3.9 rad/s.对1+α阶和2β阶低通滤波器传递函数使用两种优化方法后的指标参数值如表2所示.

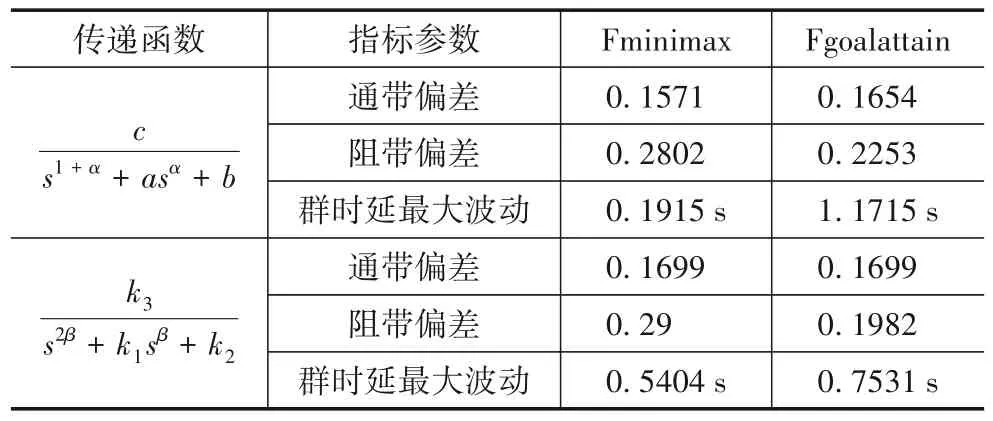
表2 第二组给定指标要求下的指标参数值

第三组：δp=0.19，δs=0.28，ωp=1.2 rad/s，ωs=4.1 rad/s.对1+α阶和2β阶低通滤波器传递函数使用两种优化方法后的指标参数值如表3所示.

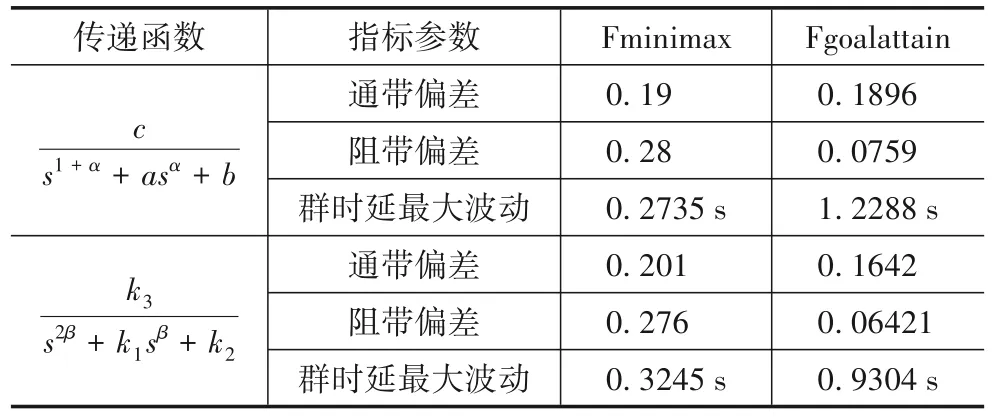
表3 第三组给定指标要求下的指标参数值

综合上述3组不同的指标要求下的优化设计，可以发现，Fgoalattain 函数优化设计的分数阶低通滤波器阻带衰减总是远大于Fminimax 函数所优化的分数阶低通滤波器阻带衰减.这是由于使用Fgoalattain 函数优化设计符合指标要求的低通滤波器时，并不像Fminimax函数在优化式（8）～式（10）或式（14）～式（16）时使其尽可能接近期望值，使用Fgoalattain 函数对式（8）～式（10）或式（14）～式（16）进行优化时，在ωp处的幅频响应是大于等于1-δp的，在ωs处的幅频响应是小于等于δs的，因此优化出的低通滤波器阻带衰减可以比给定的δs还小，同时Fgoalattain 优化的低通滤波器通带不如Fminimax 所优化的滤波器通带平坦.总而言之，在给定指标要求的条件下，使用Fminimax和Fgoalattain优化函数分别对1+α阶和2β阶低通滤波器传递函数进行优化，都可以得到符合指标要求的低通滤波器，它们的群时延也近似一个常数.可以根据实际应用需要选择优化方法：对滤波器通带平坦度和信号相位失真要求较高的可以选择Fminimax 优化函数进行低通滤波器优化设计；对滤波器阻带衰减要求较高的可以选择Fgoalattain作为低通滤波器优化设计的手段.

在不同的设计指标要求下优化得到的1+α阶和2β阶传递函数都可以用来实现符合指标要求的分数阶低通滤波器.选择Fgoalattain 函数进行优化设计时可以发现，使用2β阶传递函数所优化设计的分数阶滤波器的群时延最大波动显著的低于使用1+α阶传递函数所优化设计的分数阶滤波器的群时延最大波动.因此，若使用Fgoalattain 函数对2β阶传递函数进行优化设计，既可以使设计得到的分数阶滤波器阻带衰减较大，又可以改善使用Fgoalattain 函数所设计的分数阶滤波器信号相位失真较大的缺点.若对滤波器的信号相位失真要求较高，可以使用Fminimax 函数对1+α阶传递函数进行优化设计，既可以使设计得到的分数阶滤波器信号相位失真较小，又可以得到良好的阻带衰减特性.

在完成符合指标要求的分数阶低通滤波器传递函数优化设计后，需要进行稳定性分析以验证该滤波器是否物理可实现，在物理可实现的基础上进行电路实现和PSPICE 仿真，最后搭建实体电路进行测试，在本文第3节会给出一个设计实例.

2.2.3 与整数阶滤波器的比较分析

为了说明分数阶滤波器相对于整数阶滤波器的优势，本节通过给定的δp，δs，ωp以及ωs分别设计整数阶和分数阶滤波器并进行比较分析.此处，以整数阶Butterworth 滤波器为例来设计整数阶滤波器，利用式（17）计算Butterworth 低通滤波器的阶数并四舍五入到整数阶N，并将N代入式（18）～式（20）计算整数阶Butterworth滤波器的截止频率ωc从而设计出整数阶Butterworth 低通滤波器.并与使用Fgoalattain 函数对2β阶传递函数进行优化而设计实现的满足同样指标要求的分数阶滤波器进行比较分析.

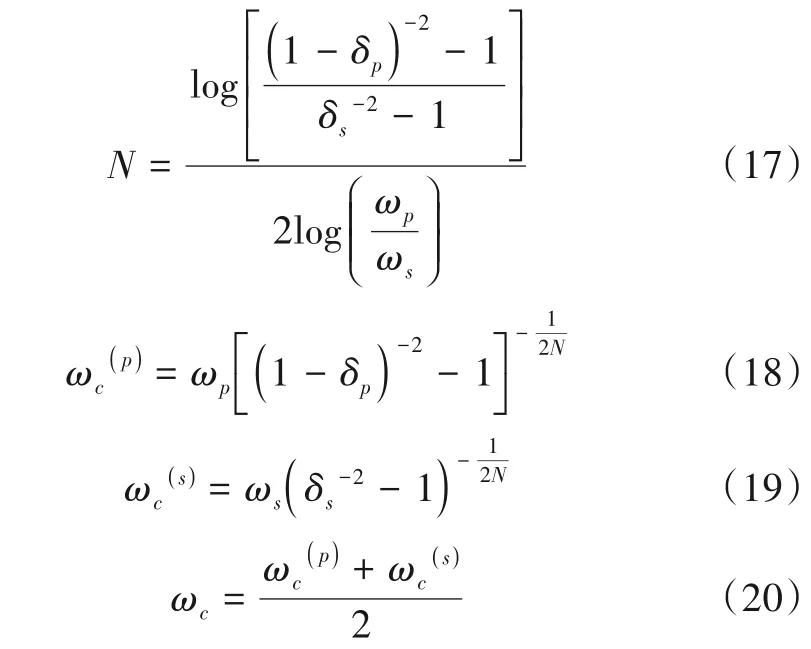
下面在亚赫兹（180 µHz～241 mHz）范围内给出3组不同的指标要求，分别设计整数阶和分数阶低通滤波器.表4 所示为设计得到的分数阶和整数阶滤波器的相关参数.

表4 分数阶滤波器和整数阶滤波器的参数

将表4 中的参数分别代入式（13）所示的2β阶低通滤波器的传递函数和如式（21）所示的二阶Butterworth低通滤波器的传递函数中.

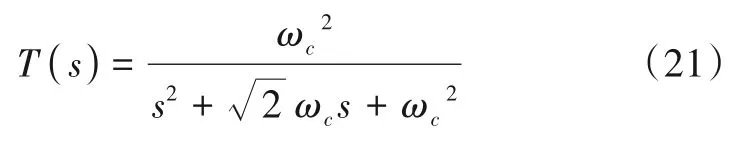
根据所得到的分数阶和整数阶低通滤波器的传递函数，在Matlab 中进行仿真并比较通带偏差和阻带偏差，结果指标对比如表5所示.

表5 分数阶滤波器和整数阶滤波器的指标参数对比

综合上述3组不同指标要求下的滤波器设计，可以发现，所设计的分数阶滤波器都可以实现给定的指标要求.而在第三组指标下，整数阶Butterworth 滤波器的通带偏差却大于所给的偏差值，不满足指标要求.并且对于通带偏差，分数阶低通滤波器比整数阶Butterworth低通滤波器的通带偏差小，也就是说，分数阶低通滤波器在通带的波动更小.此外，例如在第三组指标要求下，利用式（17）计算得到的滤波器阶数为1.5 阶，应用于整数阶Butterworth 滤波器时只能通过取整得到其阶数为2 阶，而应用于分数阶滤波器时，其阶数无须取整可以为分数.这也是分数阶滤波器相对于整数阶滤波器的优势——分数阶滤波器的设计自由度更大.

在硬件实现上来说，上述分数阶低通滤波器和整数阶Butterworth 低通滤波器都可以使用如图4 所示的KHN（Kerwin-Huelsman-Newcomb，KHN）滤波电路实现，其中C1和C2都是β（0 ＜β≤1）阶电容器.

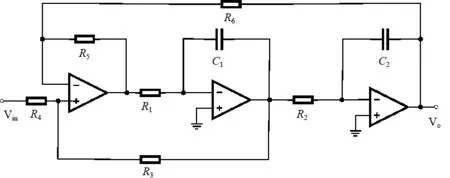
图4 KHN滤波器

当R3=R4=R5=R6时，该KHN 滤波电路的传递函数为

以第三组指标设计的两种滤波器为例，根据表4的参数得到分数阶低通滤波器和整数阶Butterworth 低通滤波器的传递函数分别为

联系式（22）～式（24）确定图4 电路中的电路元件值，如表6 所示.对于整数阶Butterworth 低通滤波器而言，ωc2=0.0036 ＜0.01.因此在电路实现时，整数阶滤波电路的C1C2R1R2大于分数阶的.

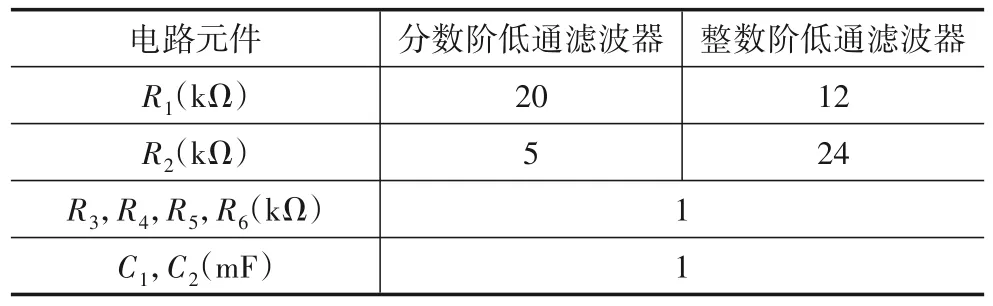
表6 电路元件取值

应用于更低频率滤波，需要的截止频率就更小，若为当前截止频率的1/100 时，根据ωnew=λωold，将频率放缩为当前的1/100（即λ=0.01），那么对于整数阶Butterworth 低通滤波器而言，有(C1C2R1R2)new=即放缩后电阻电容的乘积为放缩前的10000 倍（即）；对于分数阶低通滤波器而言，则有(C1C2R1R2)new=(C1C2R1R2)old*即放缩后电阻电容的乘积为放缩前的1584倍（即10.011.6）.放缩后电路元件具体取值如表7所示.

表7 放缩后电路元件取值

由此可知，若放缩到更低频时（即λ取更小的值），由于相比分数阶低通滤波器，整数阶Butterworth 低通滤波器在电路实现时需要较大的电阻才能实现较小的截止频率.而在实际电路中，较大的电阻会产生较大的热噪声，且运放的偏置电流流过大电阻会产生不可忽略的误差，最终影响滤波效果.此外，大电阻不利于电路的集成.因此，在极低频滤波时，分数阶滤波器相比整数阶滤波器在实际电路实现时具有优势.

2.2.4 与国外研究设计方法比较分析

如前所述，满足δp，δs，ωp和ωs这四个指标要求的分数阶低通滤波器设计方法和设计流程目前未见报道.参考文献［20］中提出了一个根据过渡带宽ε1、阻带衰减ε2、通带最大可允许峰值1+ε3以及截止频率ωc四个设计指标来设计分数阶低通滤波器的方法.为了与文献［20］中的设计方法进行比较，需要将δp，δs，ωp和ωs这四个指标转换为文献［20］的指标，转换过程中的难点是关于截止频率ωc没有直接求解的公式，故本文借用式（17）～式（20）来估计文献［20］中的截止频率，再由截止频率ωc和阻带边缘频率ωs得到指标ε1的值.由于本文关于通带最大可允许峰值要求为1，而文献［20］中的通带最大可允许峰值为1+ε3，需要进行归一化处理并将直流处作为通带最大波动处，再由δp得到指标ε3的值.最后，由ε3和δs可以确定指标ε2的值.

在将本文所给出的四个设计指标转换为适用于文献［20］的指标后，就可以用文献［20］中提出的优化设计方法设计符合指标要求的分数阶滤波器，并与用本文的设计方法所设计的分数阶滤波器进行比较分析.由于文献［20］是对2β阶传递函数进行优化设计，因此为保证对比的严谨性，本文方法采用Fgoalattain函数也对2β阶传递函数进行优化设计.对2.2.2 节中的三组滤波器进行设计的结果指标对比如表8所示.

表8 不同方法所设计的三组不同分数阶滤波器的指标参数对比

由表8可以发现，利用文献［20］中提出的优化设计方法所设计的分数阶滤波器并不能满足所有指标要求，其阻带偏差总是比要求的偏差值大，通带偏差也常常达不到指标要求.总而言之，文献［20］中提出的优化设计方法所设计的分数阶滤波器除了信号相位失真较小外，其通带和阻带偏差往往大于给出的偏差指标，不能完全满足设计指标要求，而本文所提优化设计方法则能得到满足给定指标要求的分数阶低通滤波器.并且对于给出的δp，δs，ωp和ωs这四个工程上常用的滤波器设计指标来说，使用文献［20］中的优化设计方法首先需要进行指标转换，使用起来较为烦琐，而本文所提的优化设计方法可以直接使用，更为简单.

3 设计实例

下面给出一个完整的设计流程.首先，设计指标要求为δp=0.15，δs=0.3，ωp=2 rad/s，ωs=4 rad/s.使用Fgoalattain 优化函数对1+α阶低通滤波器传递函数进行优化，优化后的传递函数参数如表9所示.

表9 给定指标要求下的1+α 阶低通滤波器传递函数优化参数值

将优化后的参数值代入传递函数中，在Matlab 中画出其幅频响应，如图5所示.

图5 1+α 阶传递函数Matlab幅频响应仿真

通过分析图5可知，该优化后的低通滤波器的通带偏差为0.0128，小于指标要求的0.15，满足指标要求；该低通滤波器在阻带边缘频率处为0.2944，小于指标要求的0.3，同样满足设计指标.

3.1 稳定性分析

分析分数阶滤波器的稳定性需要将其S 域传递函数转换为文献［21］中定义的W 平面.这可以将传递函数从分数阶转换为整数阶，以便使用传统的整数阶分析方法进行分析.可以使用以下步骤完成此分析过程：

（1）利用s=wm和α=k/m，将分数阶传递函数变换到W平面；

（2）为所需要的α值确定k和m值；

（3）求出已变换到W平面的传递函数的所有极点，如果任一极点的角度绝对值|θW|小于π/2mrad/s，那么该系统就是不稳定的；反之，若所有的|θW|＞rad/s，那么该系统就是稳定的.

将上述分析过程应用于已经优化完成的1+α阶低通滤波器传递函数的分母，如式（25）所示，得到W平面的特征方程：

其中，由于取α为0.94，因此选择m=100，k=94.求解式（26）的所有根的角度绝对值的最小值为1.2684°，其大于π/2m=0.9°.确认使用表9 中的参数的滤波器是稳定的并且可以物理实现.

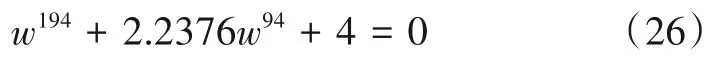
3.2 电路实现

该分数阶传递函数也能使用如图4 所示的KHN 滤波器实现，其中C1是一个常规的一阶电容器，C2是一个阻抗为ZC2=（0 ＜α＜1）的分数阶电容器.

当R3=R4=R5=R6时，该分数阶KHN 滤波器的传递函数为

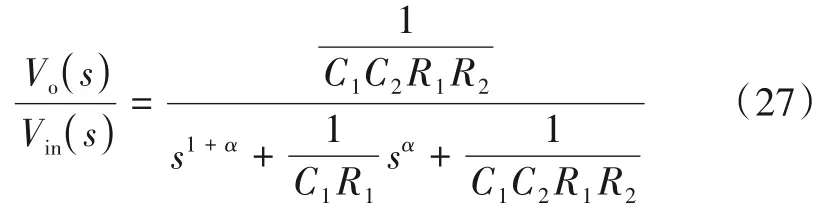
比较（27）和式（7）的系数可得出以下关系：

使用式（28）和式（29）两个设计方程确定四个电路元件值，因此在选择电路元件值以实现所需滤波器响应时有两个自由度供设计者自行确定两个元件值.同时，需要频率缩放以根据所需应用调整滤波器的工作频率.假定ωnew=λωold，可以根据下列等式缩放电路元件：

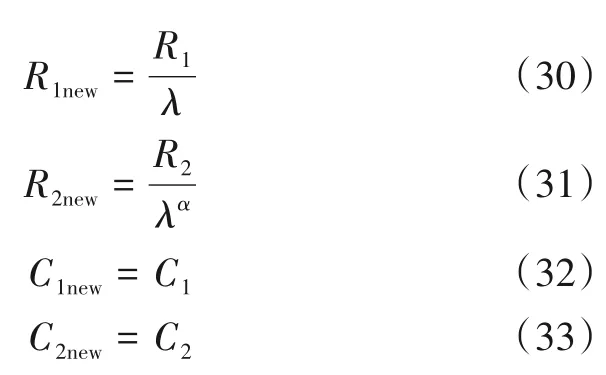
为了后续电路仿真和测试结果方便观察，使用式（30）～式（33），将优化好的分数阶低通滤波器的通带边缘频率放缩至2π×100 rad/s 时，电路中的各元件取值如表10所示.

表10 1.94阶滤波电路元件取值

3.3 PSPICE仿真

尽管在实现分数阶电容器方面已经取得了很大的进步，但目前尚无商用的分数阶电容器.可以使用整数阶电路来近似实现分数阶电容.本文利用连分式展开（Continued Fraction Expansions）来模拟实现分数阶电容.可以使用Foster Ⅰ型RC串并联网络［22］模拟0.94阶1µF电容，如图6所示，其有效频率范围为1.8 Hz至5.5 kHz.

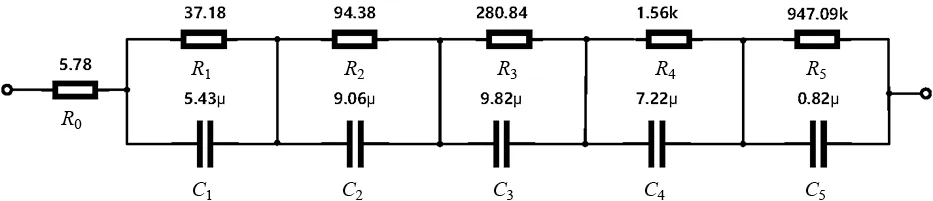
图6 0.94阶1µF电容元件模拟电路

用图6所示的0.94阶1µF的电容代替图4中的电容器C2，在有效频率（1.8Hz～5.5kHz）范围内可以当作分数阶电容来使用.根据表10电路元件值，调整图4中电路的电阻电容值，得到了的幅频响应曲线，如图7所示.

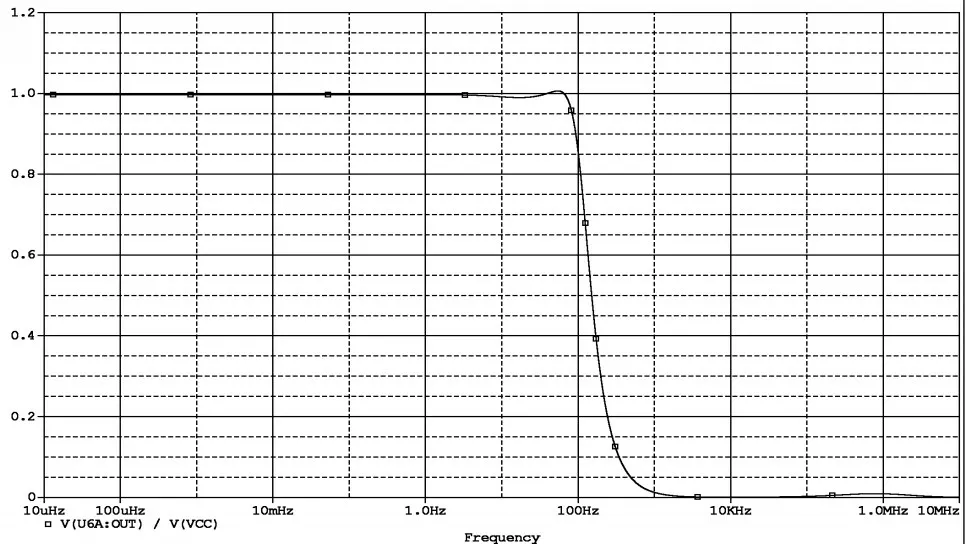
图7 给定指标要求下优化的滤波器幅频响应曲线

通过PSPICE 的数据测量功能可得，图7 幅频响应曲线的通带偏差为0.15，阻带边缘频率处为0.29，完全符合设计指标要求.阻带衰减速率约为39.3 dB/十倍频，与理论值38.8 dB/十倍频非常接近.该仿真证明，KHN 滤波电路能通过使用近似的分数阶电容器来实现符合设计指标要求的分数阶低通滤波器.

3.4 实际电路测试

本文根据图4所示电路搭建阶数为1.94、通带边缘频率和阻带边缘频率分别为100 Hz和200 Hz的符合设计指标要求的低通滤波器电路，所用运算放大器为通用型低功耗集成四运放LM324，实验电路如图8所示.

图8 搭建的1.94阶KHN滤波电路

使用Analog Discovery 2观察图8所示电路的幅频响应，响应曲线如图9 所示.通过对曲线的测量发现其通带偏差为0.17，略大于指标要求的0.15；在阻带边缘频率（200 Hz）处为0.36，略大于指标要求的0.3.该幅频响应曲线的阻带衰减速率约为36.3 dB/十倍频，比理论的阻带衰减速率小2.5 dB/十倍频率.这是由于电路中所用的分数阶电容是由RC 串并联网络模拟实现的，并非理想的分数阶电容；且电路是基于面包板用直插式电阻电容所搭建而成，测试时电阻电容本身以及外部环境的噪声等因素也会带来误差.因此本文认为所优化设计的低通滤波器的误差是在可接受范围内的，可以验证本文所提出的对于给定指标要求下的优化设计方法的有效性.

图9 1.94阶低通滤波器幅频响应曲线

4 结论

本文提出了两种对于满足给定指标要求的分数阶低通滤波器的优化设计方法并比较分析了使用Fminimax和Fgoalattain这两种优化函数所设计的滤波器各自的特点.使用1+α阶和2β阶低通滤波器传递函数并基于代表滤波器设计要求的函数组，分别建立了数学模型用以优化设计所需的滤波器.通带偏差、阻带偏差、通带边缘频率以及阻带边缘频率都可以根据实际应用进行控制以得到符合指标要求的滤波器响应.给出设计实例，应用本文所提优化方法进行优化设计和电路仿真，最后搭建实体电路进行测试，测试结果验证了本文所提方法的有效性.本文所给指标要求下优化得到的滤波器阶数都小于2 阶（1＜1+α＜2，0＜2β＜2），但某些指标下优化得到的阶数可能大于2 阶，在此情况下，可以使用阻抗变换器（Generalized Impedance Converter）来实现阶数大于1的分数阶电容，也可以将分数阶与整数阶滤波电路级联实现符合指标要求的高阶滤波器.具体实现方法将是我们下一步的研究工作.