交叉相关双路分集OAM湍流光信道接收信号模拟研究
2022-03-17熊琴琴陈纯毅于海洋姚海峰宋佳雪
熊琴琴,陈纯毅,于海洋,姚海峰,宋佳雪,娄 岩
(1.长春理工大学空地激光通信技术国防重点学科实验室,吉林长春 130022;2.长春理工大学计算机科学技术学院,吉林长春 130022)
1 引言
涡旋光束携带的轨道角动量(Orbital Angular Momentum,OAM)为光信息编码提供了新的维度资源,已成为光通信领域的研究热点[1~5].一方面,OAM 横向空间模被引入到自由空间光(Free Space Optical,FSO)通信中,发展出OAM 多路复用和OAM 开关键控等新技术,显著提升了FSO 信道传输利用率,增大了信息传输容量[2~4].另一方面,在光量子密钥分发领域,使用OAM模式可以将更多信息编码到光子中,从而增加密钥生成率[5].然而,OAM 光通信以地球大气为传输信道,该信道中存在着随机变化且不可预测的湍流,会使得通过OAM 湍流光信道的接收信号经历随机衰落.尽管OAM 横向空间模具有上述优点,但是OAM 光通信系统的性能不可避免地被大气湍流影响[6].研究具有简单性和准确性的受大气湍流扰动的OAM接收光信号模拟生成算法,可以为OAM 光通信系统的设计和优化提供参考依据,并且有助于分析评估OAM光通信系统性能.
大气湍流对OAM光通信的影响表现为信号光功率在不同OAM 横向空间模之间的随机再分布,以及随之带来的特定OAM 横向空间模携带光功率的随机起伏.目前,学者们研究了OAM 光束在大气湍流中传播的联合串扰和检测概率等[2,7],而对于受大气湍流扰动的OAM 接收光信号的研究较少.传统的受大气湍流扰动的光信号起伏概率分布模型,主要包括对数正态分布、K分布和Gamma-Gamma 分布等[8,9].而大气湍流光信道OAM接收本质上属于相干模耦合接收,与传统FSO通信接收方式具有明显差异.因此,前述传统的光信号起伏分布模型可能并不适用于OAM接收光信号起伏.在文献[10]中,具有四个独立控制参数的线性比例变换Johnson SB分布被用于描述OAM湍流光信道的随机信号功率传输系数扰动.文献[11]发现,当线性比例变换的Johnson SB分布的两个附加控制参数取值特定时,该分布无法描述OAM 功率传输系数的统计特性;并提出双Johnson SB分布模型,模拟实验表明该分布模型能够很好地描述受大气湍流扰动的OAM接收光信号起伏统计特性.
近年来,空间分集技术被广泛应用于FSO 通信中以减缓大气湍流扰动引起的接收光信号衰落,该技术也适用于OAM光通信[12,13].在空间分集OAM光通信系统中,多路OAM 接收光信号具有相同统计特性.为了使用蒙特卡洛方法评估空间分集OAM光通信系统的性能,需要模拟生成多路大气湍流扰动OAM 接收光信号.受大气湍流扰动的接收光信号属于时域自相关信号,并且多路接收光信号之间具有交叉相关性.模拟生成多路大气湍流扰动OAM 接收光信号的关键是,要使生成的每路随机光信号时域样本具有指定的自相关性,多路随机光信号样本之间具有指定的交叉相关性,并且所有信号样本序列在统计上服从双Johnson SB分布.文献[14,15]生成了具有指定归一化自相关函数且服从特定统计分布的单路时域自相关随机光信号.文献[12,16]对分集接收Gamma-Gamma 光信道进行了建模,生成了多路具有指定交叉相关系数的Gamma-Gamma 随机样本序列.虽然上述研究工作能够模拟出匹配指定相关性和概率分布的光信号样本,但它们要么只考虑单路接收光信号的自相关性,要么只考虑多路接收光信号间的交叉相关性,并不能确保多路接收光信号的自相关性和交叉相关性能同时匹配指定的目标值.准确分析空间分集OAM通信系统性能要求能模拟出自相关性、交叉相关性和概率分布都能匹配目标值的多路随机接收光信号.目前还没有文献报道如何模拟生成在统计上服从双Johnson SB分布,且满足给定自相关性和交叉相关性要求的多路大气湍流扰动OAM接收光信号.
文献[17]利用谱表示法生成了具有指定功率谱密度(Power Spectral Density,PSD)的二维高斯随机场.由于该方法需要通过傅里叶变换及其逆变换进行时频域转换,计算量大且生成的样本序列具有周期性,因此,文献[18]提出稀疏谱(Sparse Spectrum,SS)模型来模拟生成无限长的大气湍流随机相位扰动屏,并且当谱分量的数目足够大时,生成的相位扰动服从高斯分布,属于具有指定PSD 的高斯随机场.文献[17,19]通过逆变换法将具有指定谱特性的高斯随机场样本映射为服从指定概率分布的非高斯随机场样本.由于这种逆变换映射技术是非线性的,因此需通过迭代使模拟生成样本的PSD 与指定的PSD 一致[19].然而,文献[17]指出这种逆变换映射是弱非线性的,并通过仿真分析证实了单次应用逆变换映射技术产生的结果能满足绝大多数实际工程应用需求.
本文考虑设计具有指定自相关性和交叉相关性、且服从双Johnson SB分布的双路OAM 接收光信号模拟生成方法.首先,对SS 模型进行推广,生成具有指定自相关性和交叉相关性的双路高斯信号样本序列,然后再使用逆变换法把双路高斯信号样本序列变换成服从双Johnson SB分布的双路信号样本序列.本文方法支持无限长的双路OAM 接收光信号样本序列生成,且能保证双路OAM 接收光信号样本序列服从双Johnson SB分布,同时其自相关性和交叉相关性还满足指定要求.
2 理论模型
模拟生成的交叉相关双路OAM接收光信号需要满足以下三个条件:(1)每路随机信号样本序列具有指定的自相关性;(2)两路随机信号样本序列之间具有指定的交叉相关性;(3)样本序列在统计上服从双Johnson SB分布.本文提出的模拟模型分为两个步骤:首先利用推广的SS模型生成两路具有指定自相关性和交叉相关性的高斯随机信号;然后通过逆变换将前述两路交叉相关高斯随机信号映射到双Johnson SB分布,得到的满足三个特性的两路随机样本序列即为交叉相关双路OAM接收光信号.
2.1 基于推广SS 模型的交叉相关双路高斯信号生成
SS 模型相较于传统的基于快速傅里叶变换(Fast Fourier Transform,FFT)技术的模型计算量更小,且生成的二维高斯随机场样本具有样本长度不受限制的特点.对SS 模型进行推广,考虑将空间二维随机场的水平方向空间长度等效为时间长度,垂直方向的空间长度依然表示空间距离.将这种推广思想应用于SS 模型生成的二维高斯随机场,模拟生成指定空间间隔距离的双路高斯信号样本序列,示意图如图1所示.
图1(a)为SS模型模拟的大气湍流随机相位扰动屏的采样点网格,P、Q分别为相位屏的水平方向、垂直方向采样点数;图1(b)为具有指定空间间隔距离的双路信号的采样点网格.图1(a)到图1(b)的变化表示SS模型的推广过程,将SS 模型的空间采样点r(x,y)等效成所需的在时间、间距上的点Χ(ζ,d),即将SS模型空间采样点的水平方向分量x转换为等效时间方向的点分量ζ,对应的量纲由长度转换为时间,则ζm表示时刻参数,垂直方向分量y量纲无变化,用作表示距离方向的采样点分量d.点集Χd1(ζm,d1)、Χd2(ζm,d2)的等效间隔距离为l,其中,m=1,2,…,M,M表示每路信号样本序列的长度.

图1 基于SS模型的等效采样点示意图
另外,SS 模型生成的二维高斯随机场具有指定的二维PSD,可以同时控制高斯随机场水平方向和垂直方向信号的谱特性.利用推广的SS 模型,同样可以同时实现双路高斯信号的自相关和互相关.指定的高斯型归一化二维PSD写为
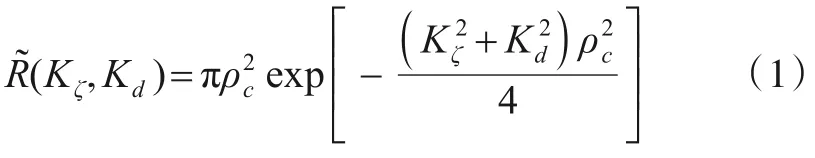
其中,Kζ、Kd分别为等效时间、距离方向的波矢分量;ρc为等效相关长度,用于表征相关性衰减快慢.从傅里叶变换得到式(1)对应的归一化自相关函数:

其中,ρζ、ρd表示等效时间、距离方向的间距.
由于SS模型通过指定的PSD 同时控制二维高斯信号行之间、列之间的相关性,二者具有相同的空间间隔距离依赖,并且列相关长度和行相关长度数值上相同.对SS 模型进行推广,将二维信号行之间的相关性等效为双路信号序列的交叉相关性,即相同时刻、不同空间间隔距离信号之间的交叉相关性,并且等效相关长度ρc表示空间相关长度,记为ρc,d.同理,列之间的相关性则等效为每路信号的自相关,表示的是同一路信号样本序列、不同时间间隔(时延)对应信号的自相关,此时ρc表示时间相关长度,记为ρc,ζ.需要注意的是,ρc,d和ρc,ζ必须取相同值.
综上所述,利用这种等效方法,由SS模型生成的二维高斯样本S(r)可直接获得所需的两路交叉相关高斯随机样本S(Χd1)、S(Χd2).最重要的是,基于推广SS 模型,可以通过改变这两路信号的等效间隔距离l来控制信号的交叉相关性,同时使得两路信号在时域上具有指定自相关性.
对SS模型推广,将在等效时间、距离位置上的采样点集的相关高斯随机信号表示为具有离散随机特点的三角级数形式,写为[18]

其中,Re(·)表示取实部;N为谱分量数;an是复白噪声随机数,其实部和虚部分别为均值为0、方差为sn/2的高斯随机数;Kn是随机波矢量,波矢的方向在[0,2π]上均匀分布,波矢的长度服从概率分布pn(K).为使模拟生成的高斯信号匹配指定的相关性,谱权重sn与概率分布pn(K)之间需满足如下关系式[18]:

其中,K0、k0分别表示低、高频截止波数.
有多种方法可以满足式(4),生成具有指定相关性的样本,其中对数均匀划分方法减小了计算量.因此,采用对数均匀方法对频谱区间[K0,k0]进行划分,将该区间分成N个子区间:

并且要求仅在第n个区间上支持概率分布pn(K),按对数均匀划分的第n个区间的频谱表示为[18]

此时,式(4)可简化为[18]

在区间Kn-1≤K≤Kn上对式(7)进行积分,推导出在第n个区间上的谱权重sn和概率分布pn(K):

进一步可得具有式(9)概率分布的随机波数幅值:

其中,v是在[0,1]范围内均匀分布的随机数.
由式(8)的谱权重,生成复高斯白噪声随机数an.根据式(10)的波数幅值和在[0,2π]上均匀分布的波矢方向θn,计算得到波矢量Kn=[xncos(θn),xnsin(θn)]T.为了便于计算,利用N×2 矩阵和2×M矩阵相乘获得N×M辅助矩阵,即

将式(3)改写为
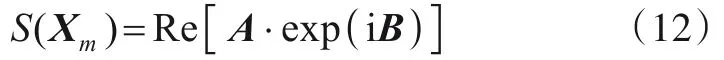
其中,波矢矩阵L=[K1,K2,…,Kn]T;采样点矩阵G=[X1,X2,…,Xm];复高斯白噪声随机向量A=[a1,a2,…,an].利用式(12)可计算出两组采样点集Χd1(ζm,d1)、Χd2(ζm,d2)对应的高斯随机样本序列S1,m、S2,m.
2.2 基于逆变换法的双路交叉相关双Johnson SB分布信号生成
逆变换法以概率积分变换定理为基础,可以将任意分布唯一映射到其他任意分布.对于相关随机样本的分布转换,这种弱非线性的逆变换映射技术同样适用.本文采用非迭代的逆变换法将两路交叉相关高斯随机信号映射为服从双Johnson SB分布的随机信号,这个过程表示为[17]

其中,FS(·)为基于推广SS模型生成的相关高斯随机样本S(X)的累积分布值;F-1(·)为双Johnson SB累积分布函数的反函数;Z表示服从双Johnson SB分布且具有指定相关性的随机过程.
双Johnson SB分布的概率密度函数(Probability Distribution Function,PDF)写为[11]

其中,4 个模型参数满足条件δ1>0、δ2>0、γ1≤γ2;pz(·)表示Johnson SB分布的PDF.由于双Johnson SB分布的累积分布函数(Cumulative Distribution Function,CDF)及其反函数F-1(·)的解析表达式未知,并且拟合这些解析式的过程较为复杂,因此,将双Johnson SB分布的CDF写为

基于图2 的框架,模拟生成双路交叉相关的双Johnson SB分布随机样本序列,具体实现步骤如下.

图2 基于逆变换法的交叉相关双Johnson SB分布随机样本序列生成框图
第一步,计算交叉相关双路高斯随机样本序列S1,m、S2,m的累积分布值序列u1,m、u2,m.
第二步,给定4 个模型参数值,通过式(16)的数值积分获得数据列表{F(zm),zm}.式(16)需要求解M个不同区间上[0,z1],[0,z2],…,[0,zm]的数值积分,为了实现一次积分调用同时求解M个不同区间上的定积分,采取换元法将多个不同区间上的积分转换到同一个相同区间上,即通过把式(16)积分上限里的变量转移到被积函数里,从而得到固定区间[0,1]上的带参数积分.通过如下公式换元:

将式(16)写为

同时获得不同积分上限zm对应的积分值F(zm),即不同区间范围的双Johnson SB分布累积分布值.
第三步,根据得到的u1,m、u2,m、{F(zm),zm},通过插值的方式模拟双Johnson SB分布CDF 的反函数F-1(·),实现相关高斯样本到双Johnson SB分布样本的映射.将F(zm)设置为样本点,zm则表示对应样本点的函数值,u1,m、u2,m作为插值点.使用线性插值获得一维函数F-1(·)在u1,m、u2,m处的函数值序列Z1,m、Z2,m,则随机样本序列Z1,m、Z2,m就具有指定的自相关和交叉相关特性,并且二者都在统计上服从双Johnson SB分布,即为交叉相关双路OAM接收光信号.
3 仿真实验与讨论
为了检验所提方法的有效性,下面通过模拟仿真实验来验证交叉相关双路OAM 接收光信号模拟模型.基于文献[18]的SS蒙特卡洛模型,设置低、高频截止波数K0=5×10-4rad/m、k0=5×104rad/m,谱分量数N=1024,信号样本序列长度M=105,空间相关长度ρc,d=10-3m,时间相关长度ρc,ζ=10-3s,时间采样间隔Δ=ρc,ζ/10=10-4s.
由于只能使用有限样本进行模拟实验分析,因此得到的随机信号相关性与理论相关性可能存在细微差异.这里从统计学角度出发,所有模拟仿真实验重复模拟100 次,并根据这100 次仿真得到的数据来计算归一化的自相关函数和交叉相关系数.
图3(a)为δ1=0.9、γ1=1.3、δ2=0.6、γ2=1.9时仿真得到的两路交叉相关OAM 接收光信号片段,双Johnson SB分布的4 个分布参数取值源自文献[11],可以看出两路信号的波动起伏随时间的变化非常相似,这是因为两路信号对应的推广SS 模型等效间隔距离非常小,并且两路仿真信号的交叉相关系数为0.988.图3(b)为对应仿真信号的自相关系数和式(2)的理论自相关系数随时延的变化曲线,表明两路仿真样本的自相关系数都与理论的自相关系数基本一致.图3(c)为对应两路仿真信号的PDF 和理论PDF 的对比曲线,它们基本重合,说明仿真信号样本序列均服从双Johnson SB分布.

图3 δ1=0.9、γ1=1.3、δ2=0.6、γ2=1.9 时的交叉相关双路OAM 接收光信号示例
为了分析推广SS模型的等效间隔距离对两路信号交叉相关系数的影响,在图3的模型参数基础上设置l=ρc,d,仿真得到的信号如图4所示.两路信号的起伏变化差别较大,二者交叉相关系数为0.327.结合图3(a)的结果,证实提出的模型可以通过等效间隔距离调节两路信号的交叉相关性.

图4 l=ρc,d时的交叉相关双路OAM接收光信号
为了进一步验证提出模型的适用性,接下来设置另外一组双Johnson SB分布参数δ1=2.6、γ1=1.3、δ2=2.7、γ2=1.9,其他参数取值同图3,该组参数下仿真得到的信号示例如图5 所示.图5(a)和图5(b)为两路信号的自相关系数和PDF 与理论的对比,可以看出仿真信号的自相关系数和PDF 分别与理论情况基本匹配,再一次说明提出模型生成的交叉相关双路OAM 接收光信号能够满足指定的自相关性和双Johnson SB分布.
值得注意的是,与图3(b)相比,图5(a)中仿真信号的自相关系数与理论自相关系数更吻合.这种情况可能与双Johnson SB分布参数的取值有关,对此,根据经验分析,这是由于图5(a)仿真信号的概率密度形状与高斯分布相似.

图5 δ1=2.6、γ1=1.3、δ2=2.7、γ2=1.9、l=ρc,d/10 时的交叉相关双路OAM接收光信号示例
另外,图5中仿真信号的交叉相关性为0.99,与图3所示的双路仿真信号的交叉相关系数相似,并且二者的推广SS模型等效间隔距离都为,进一步说明仿真的双路信号的交叉相关系数可以由该等效间隔距离来控制.
由上述仿真结果实验分析可知,两路信号的交叉相关系数与推广SS 模型的等效间隔距离有关.根据上述两组分布参数仿真生成了不同推广SS模型等效间隔距离的双路信号样本序列,它们的交叉相关系数随该等效间隔距离的变化如图6所示.当等效间隔距离为0时,双路信号样本序列的交叉相关系数为1,此时它们可以看成是同一路随机信号;随着等效间隔距离的增大,两组参数下的交叉相关系数均逐渐均匀下降;当等效间隔距离为2 mm 时,双路信号样本序列的交叉相关系数开始趋于0,到3 mm(即3ρc,d)时,相关系数几乎为0,两路信号完全不相关.
另外,结合图6 中的理论交叉相关系数变化曲线,还可以看出不同分布参数取值时,双路仿真信号样本序列的交叉相关系数与理论交叉相关系数基本一致.这说明本文所提方法仿真生成的双路信号的交叉相关性能匹配目标值;并且参数2 与理论交叉相关性的匹配度比参数1 的更好,特别是在等效间隔距离为0.5~1.5 mm 时,这是因为参数2 仿真信号的PDF 与标准高斯分布形状相似.

图6 两组分布参数对应不同等效间隔距离时仿真信号的交叉相关系数误差棒图
4 结论
本文提出一种交叉相关双路OAM接收光信号样本序列的模拟生成方法,在方法的实现过程中,通过引入矩阵相乘和换元积分减少了计算量.该方法生成的双路信号具有指定的交叉相关性,可通过设置两路信号的推广SS 模型等效间隔距离来控制交叉相关系数大小.另外,该方法能使每路信号具有指定的时域自相关性,并且信号样本序列服从双Johnson SB分布.而且,仿真模拟生成的信号样本序列长度不受限制,能够生成任意长的信号样本序列.本文的模拟仿真方法可以为用蒙特卡洛方法分析空间分集OAM光通信系统性能提供支持.
