室内可见光通信系统中基于压缩感知的空移键控信号检测方法
2022-03-17王法松张建康
左 婷,王法松,张建康,李 睿
(1.郑州大学信息工程学院,河南郑州 450001;2.河南工业大学理学院,河南郑州 450001)
1 引言
可见光通信(Visible Light Communication,VLC)是无线通信系统中一项很有前景的新型通信技术,相对于传统的射频通信有很多特有的优势,如丰富的频谱资源、良好的保密性、无许可证要求和抗电磁干扰等[1].对于VLC 的研究引起了各行业研究人员的强烈兴趣,使其成为当前无线通信领域的一大研究热点.VLC 与大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术相结合可以显著提升通信系统的传输速率,改善系统性能.基于这些优点,近年来关于室内VLC中的MIMO传输也得到了广泛研究.
空移键控(Space Shift Keying,SSK)是空间调制(Spatial Modulation,SM)技术类中设备复杂度最低也最容易实现的一种,相比较空间调制,SSK 只利用单个激活天线索引传输信息,其在室内VLC 系统中得到了广泛的应用研究[2,3].但是现有文献中关于室内VLC 系统中的SSK检测方法大都采用了极大似然(Maximum Likelihood,ML)方法,虽然检测性能是最优的,但是穷举搜索带来的计算复杂度很高,尤其是当发射端天线数较大时,计算复杂度会急剧增加[2,3].因此,在接收端找到一种复杂度低、误码性能优良的检测方案就变得尤为重要.一些线性检测算法,如迫零(Zero Forcing,ZF)检测和最小均方误差(Minimum Mean Square Error,MMSE)检测虽然复杂度较ML 有很大程度的降低,但在误码性能上与ML有较大差距,且两种算法只适用于超定系统[4].
在大规模MIMO 系统中,考虑到SSK 发射信号的稀疏特性,压缩感知(Compressed Sensing,CS)技术中的稀疏信号重构方法可在计算复杂度和系统性能之间提供一个较理想的平衡.CS 理论由Donoho等人提出[5],其中贪婪类算法是涉及稀疏信号重构的主要算法之一,常用的贪婪算法包括正交匹配追踪(Orthogonal Matching Pursuit,OMP)及其一系列改进算法[6,7].
将CS理论应用于基于SSK的射频通信已经得到广泛的研究[8~13].文献[8]在OMP 基础上将一种归一化的CS 算法用于RF 通信系统中(Generalized Space Shift Keying,GSSK)信号的解调.随后文献[9]在OMP 算法的基础上,通过在接收机使用均衡器使等效信道矩阵正交,并改善了系统性能.文献[10]通过增加迭代次数改善了GSSK系统中经典OMP算法的性能,但是误码性能会出现平台效应.文献[11]提出一种低复杂度的贪婪增强贝叶斯算法,信号的恢复精度较高.Zhang 等提出一种新的稀疏重构算法用于GSSK 信号的检测,相比现有的基于CS 的检测算法,其性能得到改善[12].与传统的CS 算法中利用内积运算找出匹配原子不同,文献[13]提出一种新的基于欧氏距离的原子匹配准则,使算法的性能和复杂度都得到改善.关于基于CS 技术在VLC系统中的应用,相关研究较少,如利用CS进行室内定位和信道估计的相关研究[14,15].此外,文献[16]提出一种基于CS 理论的湍流信道下的光SM 信号检测算法,与ML相比,极大地降低了信号检测复杂度.目前还没有发现关于在室内SSK VLC系统中采用CS算法进行信号检测的相关研究.考虑到SSK 技术的简单且便于实现特点,本文针对SSK 调制提出了一种低复杂度的基于CS 的信号检测算法,用于解调室内VLC 系统中的SSK 信号.值得注意的是,在传统的微波射频通信中,信道矩阵常服从高斯分布而满足有限等距性质(Restricted Isometry Property,RIP),这是CS 算法有效使用的前提.而室内VLC 系统的信道矩阵是由收发端位置及系统参数确定,在实际中很难判断其是否满足RIP特性,所以需要提出一种有效方法,在使用CS的稀疏重构算法之前对信道矩阵进行预处理以满足RIP性质.
本文剩余内容安排如下:第二节详细介绍室内VLC 系统的模型;第三节给出了室内VLC 系统中的CS检测算法;具体的仿真实验和参数设置将在第四节给出;最后将在第五节总结全文.
2 系统模型
2.1 室内VLC系统信道模型
在室内VLC系统中,发光二极管(Light Emitting Diode,LED)作为发射端,在提供照明的同时可以进行高速短程通信[17],接收端利用光电检测器(Photo-Detector,PD)接收信号.假设在室内VLC 系统的发射端配备Nt个LED,在接收端的PD 个数为Nr,本文考虑常用的强度调制/直接检测(Intensive Modulation/Direct Detection,IM/DD).在所考虑的系统中,进一步假设所有的LED 都用来执行照明功能,照明的光功率为I.而在被激活的LED 上实施IM 用来传输信息以实现通信功能.激活的LED 发射一个强度为Im∈M 的符号,M 是所有可能发射信号强度水平的集合,可以表示为Im=m=1,2,…,M,M表示强度调制的阶数,Ip表示发射信号的平均光功率,未被选择发送信号的LED 只用来照明.
由于光传播特性,室内VLC 系统接收端接收到的信号包括直视(Line of Sight,LoS)分量和非直视(Non-Line of Sight,NLoS)分量.LoS 是指LED 发送的信号直接被PD 接收,而NLoS 是指LED 发出的光信号经过物体发生折射或反射后到达接收端,对于室内VLC 系统,由于房间的墙壁反射,接收端的PD 接收到的光信号是LoS 分量与多个非NLoS 分量之和.但是LoS 链路在接收端上的总接收光功率超过95%[18],而且即使最强的非NLoS 分量仍比LoS 分量至少低7 dB[19].因此,当考虑将发射端LED 安装在服务区域的天花板上并朝下时,可以近似忽略非NLoS 成分,而只考虑LoS 进行分析[20].假设LED 具有广义朗伯发射模式,图1 给出了LoS传输的几何模型.
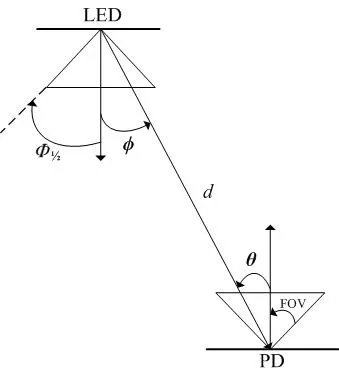
图1 LoS传输几何模型
其中ϕ为LED 的出射角,θ为光在PD 上的入射角,FOV为接收端的视场角,为LED的半功率角,d为收发端之间的直线距离.模型中LED和PD之间的信道增益可表示为
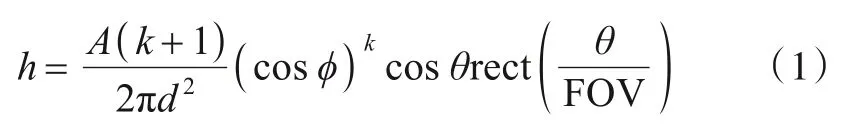
其中A为接收端PD 的面积;k为辐射波瓣的模数,可以表示为k=;rect(·)函数表示当PD 的入射角大于FOV 时,PD 不能接收到光信号,此时LED 与PD 之间的信道增益h为0.Nr×Nt的光MIMO 信道矩阵H可以表示为

其中hij表示第j个LED 和第i个PD 之间的信道增益.接收端的接收信号为

x是Nt×1维的发送信号向量.是包含散粒噪声和热噪声成分的高斯白噪声向量[18],其中为Nr×1维零值列向量,为Nr×Nr维单位矩阵.
2.2 室内VLC系统中的SSK调制技术

作为一项特殊的MIMO 技术,SSK 无须消耗额外功率,每时隙只激活一个LED 携带信息,在实际应用中可以节省很多硬件开支,其在每时隙传输信息的比特位数为.表示向下取整操作.下面将从实例出发分析基于SSK的VLC系统中发送信号的产生过程.假设Nt=4,则一个SSK符号携带=2 bit信息.定义激活天线索引与传输信息比特之间的映射准则为(1)→[0 0],(2)→[0 1],(3)→[1 0],(4)→[1 1],其中(i),i=1,2,3,4 表示天线索引.因为SSK 只利用激活天线编号发送信息,不妨假设发送的符号强度都为1,这样所有可能发送的信号列向量表示为矩阵形式为

3 VLC系统中的CS检测算法
由CS 理论可知,为了精确恢复原始发射信号x,测量矩阵H需要满足RIP 性质[5,6,21].但在室内VLC 系统中,由于信道矩阵的特性,很难直接判断测量矩阵是否满足RIP 性质.在射频通信中,信道矩阵通常是高斯随机矩阵,研究表明此类矩阵可以以很大概率满足RIP性质[21].但是,本文考虑的室内VLC 信道则不同,信道矩阵完全由LED 和PD 位置和相关参数决定,信道矩阵元素是确定的,所以不能保证该测量矩阵(信道矩阵)H满足RIP 性质,若直接使用CS 算法,在测量矩阵H不满足RIP 性质的情况下,如本文在仿真实验部分得到的结果所示,得不到理想的信号检测性能,从而无法恢复出原始发送信号.针对本问题,本文提出了一种测量矩阵预处理方法,在此预处理方法的基础上,进一步提出了一种基于稀疏性的信号检测算法.
3.1 测量矩阵的SVD预处理
考虑如式(3)的测量信号模型,为了分析方便,分析过程不考虑噪声的影响.首先,由于测量矩阵行满秩,基于奇异值分解(Singular Value Decomposition,SVD)可以分解为

令Z=Δ*UTH,其为部分正交矩阵,则得到

进一步,利用式(6),可将Z简化为

此外,由Z定义预处理后的测量矩阵HSVD为

其中z1,z2,…,为矩阵Z的 列向量,‖·‖为向量的Euclidean 范数,则有
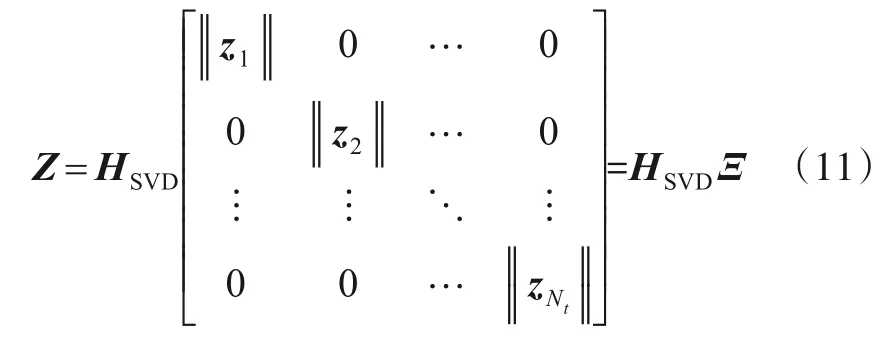
则得到预处理后的接收信号可以表示为
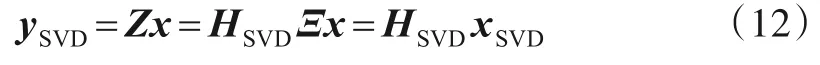
其中

可以看出,式(13)有两个特点:一方面,xSVD只是x的一个缩放版本,因此它保持与x相同的稀疏结构;另一方面,HSVD是一个部分正交矩阵,满足RIP 性质,并在CS理论中得到了广泛应用[21].因此,通过求解稀疏优化问题,正确重构xSVD后利用式(14)可以得到原始信号的估计,即

3.2 基于CS的信号检测算法
常用的CS 稀疏重构算法有两大类:凸优化算法和贪婪算法.凸优化算法重构效果好,但是其计算复杂,计算量大.贪婪算法通过选择最匹配的原子参与迭代,直至逼近原始信号.常用的贪婪类算法主要包括OMP 算法[6]和压缩采样匹配追踪(Compressed sampling matching pursuit,CoSaMP)[7]算法等.针对本文考虑的室内VLC 系统,将采用经典的OMP 和CoSaMP 算法重构原信号,同时还将提出一种OMP-ML 联合检测算法.OMP-ML 联合检测算法的具体流程为:每次迭代选取与矩阵H的K个最相关列放进索引集,选取最大相关列进行信号估计和残差更新,经过1 次迭代后就会有1 个索引集,每个索引集包含K个元素.在所有索引集元素中任选1 个元素进行组合,所有组合数不会超过K,再对这些组合进行最优搜索找出最优的激活天线组合.与OMP 不同,每次选取多个相关原子数在一定程度上更大概率包含激活天线的位置,将迭代所得的候选索引集进行遍历,这样,相比OMP 算法,所提出的改进算法重构效果将会得到改善.K决定了算法的复杂度和性能,本文取K=2 时性能和复杂度都处于一个理想的状态,算法1 给出了算法的详细步骤.

如上文所述,通过对室内VLC 系统中的测量矩阵H等进行预处理后,可以利用CS 的稀疏重构算法对基于SSK 的室内VLC 系统接收端信号进行检测,整个检测算法流程如算法2所示.
3.3 复杂度分析
由于室内VLC 系统中的信号和信道矩阵都是正实数,本文将从浮点运算的角度分析ML 和基于CS 的稀疏信号重构算法的复杂度,具体的复杂度分析如表1所示,其中,SVD 计算的复杂度和矩阵求逆属于一个运算量的计算级别,而SVD 预处理只需要一次操作,所以其复杂度在此处可忽略不计.表格中的复杂度分析结果中的参数同前文,其中ML 检测算法中η=表示系统的频谱效率.

表1 SSK调制的各种检测算法复杂度分析
按照本文中的仿真实验设置,当Nt=16,Nr=9 时,ML 浮点运算次数为4880,OMP-ML 为944,而CoSaMP的浮点运算次数为723.两种CS算法复杂度相比ML 下降了约80%和85%,图2给出了SSK 调制技术各检测算法的浮点运算次数随Nt变化的规律.可以观察到,随着发射端个数的增加,ML与各CS算法的浮点运算复杂度差距也随之增加.


图2 SSK调制方案各检测算法在不同Nt时的浮点运算次数
4 仿真分析
本部分将分别采用ML、OMP-ML、OMP 和CoSaMP四种算法对SSK 调制传输信号进行解调,并考虑不同系统参数设置下对误码率的性能进行仿真分析.在接收端对信号进行解调时,OMP、CoSaMP和OMP-ML算法的迭代次数均为SSK 信号的稀疏度k,即取值为1.此外,OMP-ML 算法迭代过程中选择的相关原子数K取值为2.
在SSK 调制方案中,发射端Nt=9,Nr=4,接收端位置固定,表2 给出了实验中的各仿真参数,在下面的仿真中若不作特别说明,Φ12取值为15°.为了保证CS 算法能够有效使用,需要保证测量矩阵H满足RIP 性质,所以在执行基于CS 的检测算法时,需要先将信道矩阵进行SVD 预处理后再使用CS的稀疏重构算法.下面分别对测量矩阵H经过SVD 预处理和未经处理两种情况下CS 算法的检测性能进行仿真分析,以验证本文提出的测量矩阵预处理方法的有效性.图3 给出了测量矩阵H未经预处理的仿真结果.

表2 SSK调制系统的仿真参数设置

图3 H未经SVD预处理时采用贪婪类算法及ML检测算法的仿真结果,其中Nt=9,Nr=4
从图3 结果可以看出,当H未经SVD 预处理时,基于CS 稀疏重构的贪婪类算法几乎无法重构原始信号,说明此时测量矩阵不满足RIP 性质,CS 的稀疏信号重构算法无法使用.图4、图5 是H经SVD 预处理后的仿真结果,在其他参数给定的情况下,给出不同半功率角配置下系统的仿真性能变化,Φ12分别取15°,30°,45°和60°.
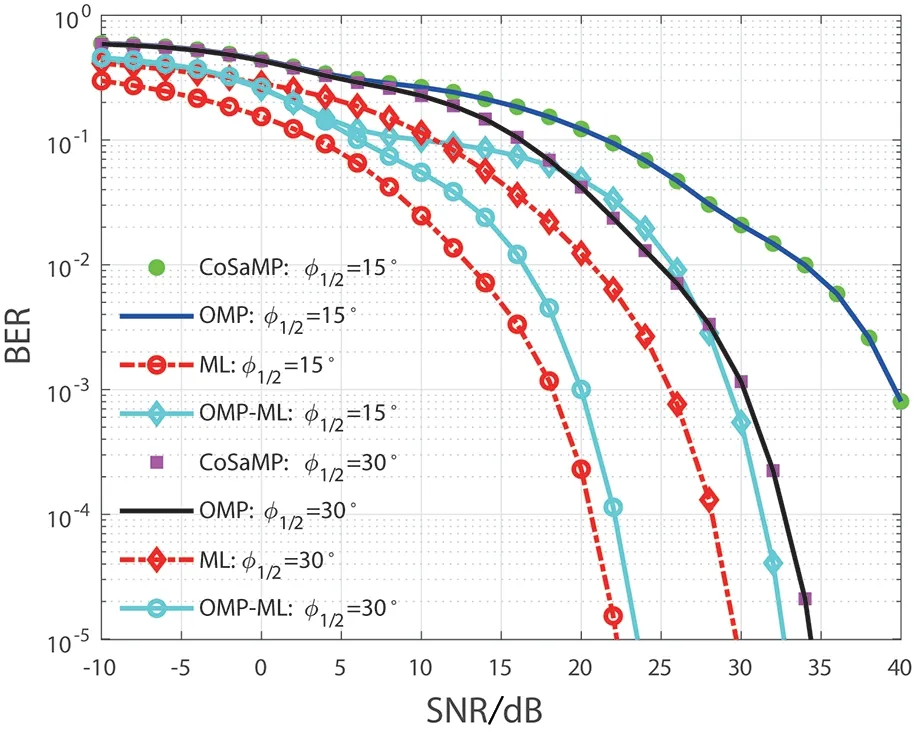
图4 ML 和基于测量矩阵SVD 预处理的CS 贪婪类检测算法性能随Φ1/2变化的情况,其中Nt=9,Nr=4,Φ1/2=15°、30°

图5 ML 和基于测量矩阵SVD 预处理的CS 贪婪类检测算法性能随Φ1/2变化的情况,其中Nt=9,Nr=4,Φ1/2=45°、60°
当对测量矩阵进行SVD 预处理以使其满足RIP 性质后,CS算法的性能得到显著改善.由图4、图5的仿真结果可以看出,随着的增大,ML 检测性能逐渐变差,这是因为随着的增大,辐射波瓣模数减小,进而影响信道增益,信道增益减小就会导致系统的误码性能衰减.而OMP、CoSaMP 和OMP-ML 算法却能实现原始发射信号的有效检测,这是因为,贪婪类算法的保障条件是信号的稀疏性和测量矩阵满足RIP性质,只要这两个条件满足,稀疏重构算法就能以很高的概率恢复出原始稀疏信号.而ML 和基于CS 的算法解调原理不同,ML 主要依赖于最小二范数的求解,所以解调性能与信道增益关系密切,而CS 算法主要受信号稀疏性影响.另外,因为SSK 的稀疏度为1,所以CoSaMP 算法本质上退化为OMP 算法.故两种算法在恢复原始信号时的性能相同,图中表现为两条性能曲线重合.OMP-ML性能比OMP 好,但是复杂度有所增加,此外,随着的增加,ML 和CS 误码性能差距逐渐变小,当增大到某个值后CS 算法要稍优于ML,如图5 所示.在实际应用中半功率角都设置较大,所以本文提出的CS 算法更加实用.
为了进一步分析算法性能,下面将针对LED 间距取不同值,分别采用CoSaMP、OMP、OMP-ML 和ML 检测算法,对系统的性能进行仿真分析.LED 间距d分别取为0.8 m、1 m、1.25 m.假设LED 在同一水平面上x轴和y轴坐标的分布范围分别对应为以下三种情况:[1.2 2.0 2.8]m;[1.2 2.2 3.2]m;[1.25 2.5 3.75]m.设 为60°.仿真结果如图6所示.
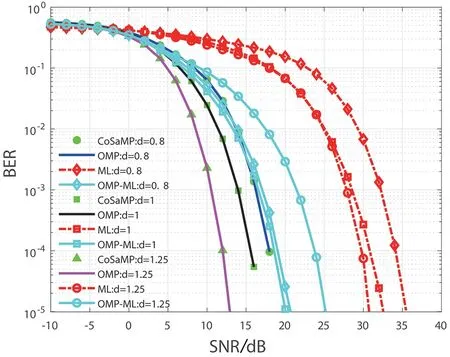
图6 ML 和基于测量矩阵预处理的CS 贪婪检测算法的BER 性能随LED间距变化的情况,其中Nt=9,Nr=4,Φ1/2=60°
从图6 的仿真结果可以看出,随着LED 间距的增加,ML 检测性能逐渐改善,这是因为降低的信道相关性可以带来更好的误码性能.OMP 和CoSaMP 算法性能随LED 间距变化的规律也类似ML,同样误码率下,这两种CS 检测算法的信噪比增益比ML 高近20 dB,其主要原因是两类检测算法的解调原理不同.具体地,基于CS 的稀疏信号重构算法在进行相关稀疏采样或者对测量矩阵预处理时,滤掉一些非采样点(观测点)的噪声,然而ML 检测算法的解调原理就是通过穷举搜索枚举.当待重构信号足够稀疏且信道本身质量不好时,非采样点就会附加很大噪声,从而使ML的检测性能急剧下降.同时,由于发射端LED 数目较大时,基于SSK 调制的信号稀疏性强,所以ML 的检测性能要弱于基于CS 的信号检测算法.而基于CS的检测算法在稀疏采样时会有效抑制这部分噪声,相当于间接提高了信噪比,所以有更好的检测性能.从仿真结果可以看出,针对SSK 类调制技术,OMP 和CoSaMP 算法和本文提出的OMP-ML 算法在性能和复杂度上都较ML 检测更为理想,是合适的检测方法.
为了验证本文提出的基于CS 的解调算法在室内SSK VLC 系统中的普适性,通过以下仿真实验研究了不同LED、PD 数目和结构布局对各解调算法性能的影响,图7 给出了几组LED 及PD 分布实验的俯视图.
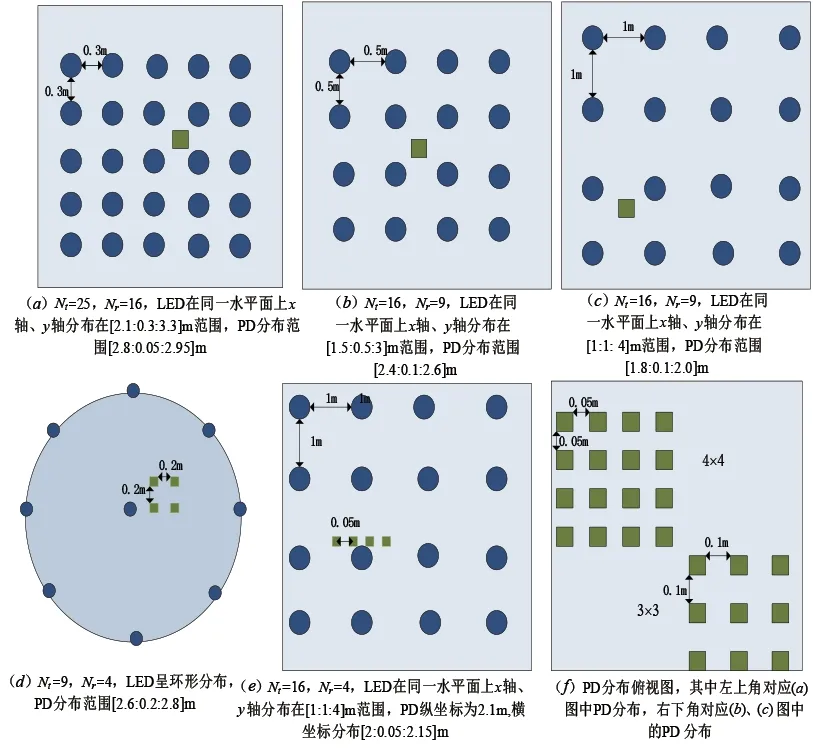
图7 不同数目和分布下的LED和PD布局
其中圆形代表LED,图7(a)、图7(b)和图7(c)中正方形表示PD 阵列分布区域,为了进一步表示PD 阵列的详细分布情况,在图7(f)中给出了图7(a)、图7(b)、图7(c)中的4×4 和3×3 的PD 阵列分布详情.在实际应用场景中,用户接收端设备通常是手机或者笔记本等设备,所以PD 的分布范围受限,所以在本文中设置在20 cm×20 cm 范围内.根据以上布局,得到相应的仿真结果如图8所示.

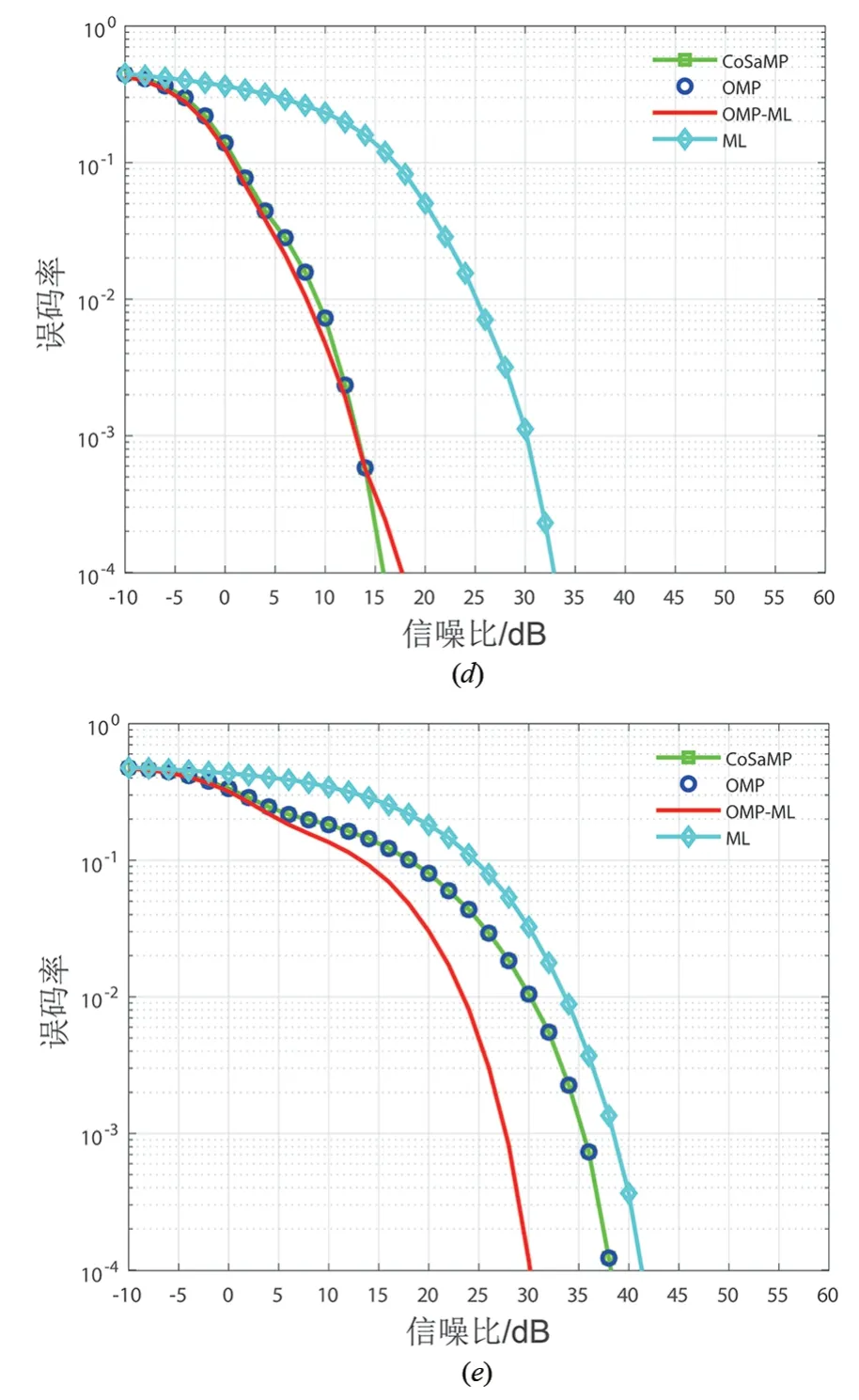
图8 ML 和基于测量矩阵预处理的CS 贪婪检测算法的BER 性能随LED和PD数目及布局变化的情况,其中Φ1/2=60°
从仿真结果可以看出,增加LED 个数,信号的稀疏性变强,OMP 和CoSaMP 算法性能增益都得到提升,同样LED数目下,当PD个数较小时,OMP-ML算法性能最优.对于不同的LED 和PD 布局和规模,CS 类算法的解调性能均优于ML 解调算法,进一步证实了所提CS 算法在室内SSK VLC系统的适用性.
根据上述仿真结果,可以得出以下结论:对于室内VLC 系统,在对信道矩阵进行SVD 预处理后,本文提出的稀疏重构算法能够以较高的准确率恢复原始发送信号,系统的误码性能可以获得比ML 更好的水平,且检测复杂度也有明显降低.在实际应用场景中,可以根据室内照明的具体参数设置选择更合适的检测算法,显然本文提出的CS 检测算法更适合LED 数目较多且半功率角设置较大的情形.当半功率角和LED 个数都设置较小时,ML 检测算法能够实现更理想的室内VLC.
5 结论
本文针对室内VLC 系统中SSK 调制信号的稀疏检测问题,提出了一类基于CS的稀疏信号检测算法,主要解决了以下两个问题:首先,通过对测量矩阵的SVD 预处理,使其能够满足RIP 性质,为下一步提出基于CS稀疏重构算法的信号检测方法奠定了理论基础;然后,提出了一类针对室内VLC 系统中SSK 调制信号的稀疏检测算法,该类算法与基于ML 的检测算法在原理上具有本质的区别,在MIMO情况下的误码率和计算复杂度两方面性能均有效提升.此外,从仿真结果可以看出,基于SSK 调制的室内VLC 系统参数配置对系统的误码性能影响较大,因此给出了在不同情况下的最优参数选择方案.同时,通过理论分析和仿真验证,本文提出的基于SVD 的测量矩阵预处理的稀疏信号检测方案,在提供良好性能的同时可以降低检测算法的计算复杂度,尤其适合发射天线数量较大的大规模MIMO系统.
