基于改进SSD-Teager时频分析的引风机转子故障诊断方法

唐贵基，孙军科，，王晓龙，伍小林，周福成，崔彦亭，吴 韬，胥佳瑞

（1. 华北电力大学 机械工程系 河北省电力机械装备健康维护与失效预防重点实验室，河北 保定 071003；2. 中国大唐集团科学技术研究院有限公司 火力发电技术研究院，北京 100040）

0 引言

我国电力工业发展迅速，根据中国电力企业联合会发布的《2019—2020年度全国电力供需形势分析预测报告》［1］统计结果，2019年全年全社会的用电量为7.23×1012kW·h，相比上年增长了4.5%。截至2019年底，全国全口径发电装机容量为2.01×109kW，其中火电装机容量为1.19×109kW，水电装机容量为3.6×108kW，核电装机容量为4.874×107kW，并网风电装机容量为2.1×108kW，并网太阳能发电装机容量为2.0×108kW，占比分别为59.2%、17.9%、2.4%、10.4%、9.9%，由此可见在未来一段时间内，火力发电仍将占据我国电力供应的主导地位。汽轮发电机组、风机、给水泵等旋转机械作为火力发电厂的主要设备对电力生产的重要性不言而喻，其转子更是重中之重，转子承受蒸汽对工作叶片的回转力并作为重要的负载和传动结构，它的运行状态将直接影响整个发电系统，因此，对转子进行故障诊断具有重要的现实意义与经济价值［2］。

常见的转子故障类型包括动静碰摩、油膜涡动、油膜振荡、裂纹、不平衡、不对中等［3-4］。大量研究表明转子故障振动信号通常为非平稳多分量耦合信号［5-7］，由于时频分析方法能同时提供振动信号的时域和频域信息，因而在转子故障诊断领域中得到了广泛的应用，探究行之有效的时频分析方法成为国内外学者的研究热点。希尔伯特-黄变换HHT（Hilbert-Huang Transform）是近年来信号处理领域常用的时频分析方法之一，它由经验模态分解EMD（Empirical Mode Decomposition）和希尔伯特变换HT（Hilbert Transform）两部分组成［8-9］。文献［10］利用HHT 清晰地表征了横向裂纹转子的扭振所形成的相位调制现象，为转子裂纹故障的预测和诊断提供了有效的方法。文献［11］基于HHT 的思想和Teager 能量算子在一定程度上改善了HT 存在的端点效应，提出了Teager-Huang 时频分析方法用于转子碰摩故障诊断，但所使用的信号分解方法为EMD，其存在模态混叠、包络拟合时易出现端点效应等问题，从而影响分析效果［12］。文献［13］针对局部特征尺度分解LCD（Local Characteristic-scale Decomposition）方法的分解精度不足这一缺陷，提出了基于分段多项式的局部特征尺度分解PPLCD（Piecewise Polynomial based Local Characteristic-scale Decomposition）方法，并成功应用于转子碰摩故障诊断。文献［14］针对转子疲劳裂纹、动静碰摩和转子-轴承系统不平衡3 类故障振动信号特征提出了基于局部均值分解LMD（Local Mean Decomposition）的时频分析方法。文献［15］将互相垂直方向上的振动信号组成复数信号，利用复局部均值分解CLMD（Complex Local Mean Decomposition）对合成复数信号进行自适应分解，实验结果表明该方法可准确诊断滚动轴承微弱故障和复合故障。EMD、LCD 和LMD 方法的基本原理均是基于极值点拟合的递归分离方法，当待分解的信号中存在噪声、间断信号等异常事件干扰时，其分解所得的本征模态函数IMF（Intrinsic Mode Function）分量波形易发生畸变，从而出现模态混叠现象，如何避免或解决模态混叠现象是目前信号处理领域的一个重要研究方向。

P. Bonizzi 等人［16］于2014 年提出了一种以奇异谱分析为基础的信号分析处理方法——奇异谱分解（SSD）方法。SSD 方法不同于EMD 方法通过极值点拟合实现信号分量的提取，其核心思想是通过奇异值分解从频带的划分和筛选角度去实现特定信号分量的重构，此重构方式使得SSD 能较好地抑制伪分量的产生和模态混叠现象的出现，表现出了较好的鲁棒性。但该方法以迭代残余分量与原始信号的能量比作为迭代停止条件，不具有稳定性，且针对转子类振动信号，该方法在分解过程中的残余分量与原始信号的能量比不易控制。若能量比阈值设置过大，则易导致信号分解不充分，出现欠分解的现象，掩盖包含故障特征信息的分量成分；若能量比阈值设置过小，则可能会出现过分解的现象，产生过多的虚假分量，导致计算效率低，且会给后续分析带来极大的不便。针对该缺陷，本文提出了融合互信息判据和能量比的循环迭代协同控制策略，对SSD 方法进行改进，并与Teager能量算子解调算法相结合，提出了基于改进SSD-Teager时频分析的转子故障诊断方法，并应用仿真信号和现场实测信号对该方法的有效性及优越性进行验证。

1 基于改进SSD-Teager时频分析的转子故障诊断方法

1.1 SSD方法基本原理

SSD 方法通过迭代循环可将非线性非平稳信号分解为按由高频到低频顺序排列的奇异谱分量SSC（Singular Spectrum Component），具体分解步骤如下［16］。

矩阵X左侧区域的3行3列部分为轨迹矩阵，将X的右下角3个元素移至矩阵左上角位置，从而得到式（2）所示的新矩阵。

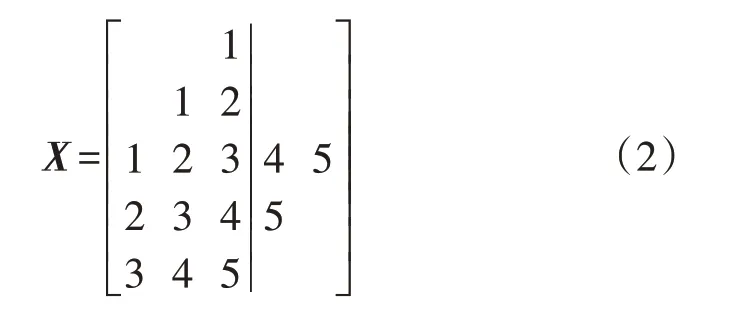
新矩阵中各对角线元素相同且数量相等，其中矩阵左侧区域为所构建的新轨迹矩阵Y，该构造方式增强了原始信号中的振荡成分，并使得迭代后残余分量的能量呈现递减规律。

2）自适应选择嵌入维数M。

首先由式（3）计算第j次迭代运算时的残余分量υj(n)：

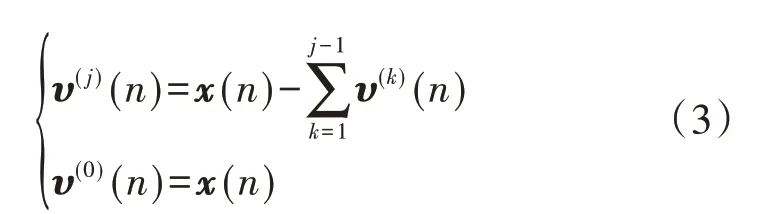
然后再估计功率谱密度最大峰值处对应的频率fmax。在第1 次迭代过程中，若fmax/fs（fs为采样频率）小于给定阈值，则可将残余分量视为一个大趋势项，此时设定嵌入维数M=N/3；否则，在j ＞1 的情况下，嵌入维数M=1.2fs/fmax。

3）重构第j个SSC。若在第1 次迭代过程中就检测到大趋势项，则计算矩阵X1=σ1u1vT1（其中，σ1为所构造的第1 个高斯函数的带宽，u1为高斯函数的谱模型拟合的功率谱密度轮廓，v1为第1 次迭代运算时的残余分量），对X1进行对角平均得到分量序列时间尺度g()1(n)；否则执行下一次j ＞1 时的循环，使用左特征向量在频谱[fmax-Δf，fmax+Δf]（Δf为残余项功率谱密度中主峰的半带宽）范围内具有突出主频率的所有特征组和对选取模态分量的主峰能量贡献最大的一个特征组，创建子集Ij={i1，i2，…，ip}（is（s=1，2，…，p）为所提取的特征组，p为所有特征组的数量），然后通过矩阵XIj=Xi1+Xi2+…+Xip的对角平均来获得相应的SSC。

4）迭代停止条件。在分解过程中得到分量序列时间尺度g(j)(n)的同时会产生一个残余信号分量υ(j+1)(n)=υ(j)(n)-g(j)(n)，由式（4）计算残余分量与原始信号的归一化均方值误差λ(j)NMSE。

式中：m为SSD得到的SSC数量。

1.2 改进SSD方法

由SSD 方法原理可知，处理信号时其迭代停止条件能量比阈值λth需预先设定，该值设定合理与否将直接影响分解效果以及SSC 数量，然而受不同设备、不同工况的影响，λth值通常难以准确设定。针对这一问题，本文提出一种融合互信息MI（Mutual Information）判据和能量比的循环迭代协同控制策略，对SSD 的信号处理过程进行改进。该策略的核心思想是通过互信息计算结果甄别SSD 过程是否产生虚假分量，从而实现循环迭代过程的有效控制，同时为避免由于无法满足互信息判定阈值下限而陷入无限死循环，利用能量比指标作为辅助控制条件来强制结束迭代过程。

互信息引申于信息论中熵的概念，用于判断2个随机变量A与B之间的相关性，能够定量地表示二者的相互依赖程度，比相关系数和互相关函数法更能表征不同变量间的相关程度［17］，互信息表达式为：

对互信息进行归一化处理后，将其用于判断分解残余分量与原始信号的相关性，当最小归一化互信息值低于设定阈值时，认为残余分量不再蕴含故障特征信息，原始信号已被充分分解，从而结束整个运算过程，即可根据实际分析信号自适应地控制SSD 方法的迭代过程。参考相关文献［17-19］中的阈值设定范围，并通过多组不同类型仿真信号进行分析验证，综合对比发现，当互信息判定阈值为0.05时，改进SSD 方法普适性最佳，因此本文中设置互信息判定阈值为0.05。基于互信息判据和能量比协同控制策略的改进SSD 方法流程图见附录A 图A1，具体实现步骤如下：

1）初始化i=1，设置SSD 方法的迭代停止条件能量比阈值=0.1，搜索范围从0.1 开始至0.001 结束，搜索步长为0.001；

2）设定第i次迭代分解的输入信号xi(t)，加载原始振动信号x(t)，x1(t)=x(t)，通过自适应选择嵌入维数M构造新矩阵X，进而获取新轨迹矩阵Y，对Y进行SSD 重组，将信号xi(t)分解为mi个SSC（j=1，2，…，mi）和1个残余分量ri(t)；

6）结束整个循环输出结果，得到n个SSC。

1.3 改进SSD-Teager时频分析方法

Teager 能量算子是一种非线性算子，其通过对振动信号的瞬时值及其微分进行非线性组合放大信号的瞬时能量成分，从而增强信号的冲击特征，适用于检测信号中的冲击成分，且Teager 能量算子的包络解调效果相比HT 具有更高的时间分辨率［20-21］。基于此，本文将Teager能量算子与改进SSD方法相结合，提出了一种基于改进SSD-Teager时频分析方法。

对于连续时间信号x(t)，Teager 能量算子ψ的定义为［22］：

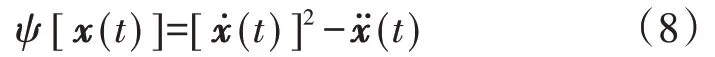
离散信号x(n)的Teager 能量算子ψ[x(n)]定义为：

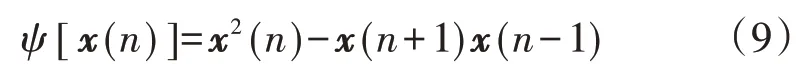
由式（9）可知，任一时刻Teager能量算子的计算仅需连续3 个样本数据即可，计算量较小且计算效率高。

利用Teager 能量算子进行解调计算，通过式（10）、（11）可以分别得到信号x(t)的瞬时频率、瞬时幅值。

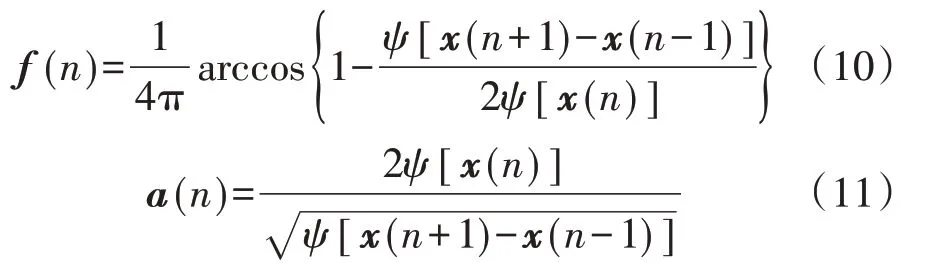
由式（10）和式（11）可了解信号的时频分布信息，有利于信号特征的准确辨识，因此本文将改进SSD 方法与Teager 能量算子解调算法相结合，利用改进SSD 方法对多分量信号进行处理，自适应得到若干个SSC 后，分别计算各SSC 的瞬时幅值和瞬时频率，并将所有SSC 的时频分布特征进行集合汇总，绘制得到多分量信号的Teager 时频谱，从而获得其完整的时频分布特征信息。

1.4 故障诊断流程

改进SSD-Teager 时频分析方法用于转子故障诊断时的具体流程为：

1）利用改进SSD 方法对传感器采集的引风机转子故障振动信号进行分解处理，得到一系列按由高频到低频顺序排列的SSC；

2）利用Teager 能量算子解调求解每个SSC 的瞬时幅值和瞬时频率，得到各个分量的时频表示；

3）将所有SSC 的时频分布进行汇总，得到对应的时频图，并根据所得信号的整体时频特征判断转子故障状态。

2 仿真信号分析

为验证本文所提方法的分解效果和时频分析能力，构造一含有随机噪声的多分量信号x(t)，该信号由1个低频谐波分量x1(t)、2个频率成分不同的调频信号x2(t)和x3(t)以及随机噪声x4(t)叠加而成，具体表达式为：

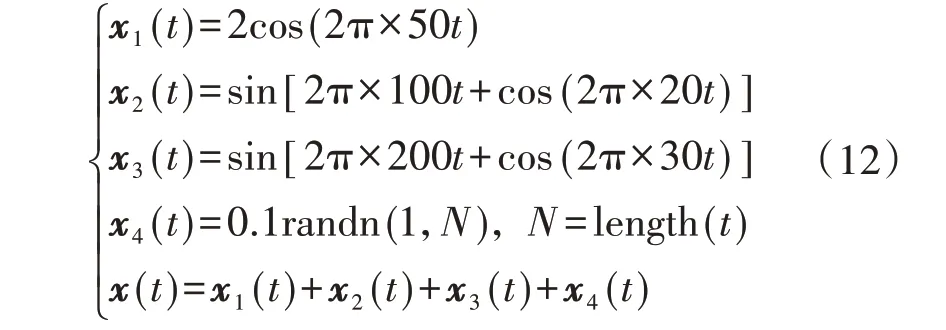
式中：t∈[0，0.25]s；分析点数N=1024；randn(1，N)表示生成1 行N列服从均值为0、方差为1 的正态分布的随机数；length(t)为时间t内的数据长度。合成信号x(t)及各分量信号的时域波形如图1 所示，信号采样频率fs=4096 Hz。

图2 是利用本文所提改进SSD 方法对仿真信号x(t)进行分析后所得分解结果，共得到3 个SSC。由图可见，SSC1、SSC2、SSC3分别对应x3(t)、x2(t)、x1(t)这3 个信号分量，可见本文所提改进SSD 方法能准确地将信号分量按照由高频到低频的顺序排列，同时能自适应地将随机噪声信号分量x4(t)视为残余分量不纳入分解结果中。对改进SSD 方法所得分量进行Teager能量算子解调得到的时频分布图见附录A 图A2，由图可清晰地看出各分量频率成分以及频率调制现象。

同时为了证明本文所提改进SSD方法的优越性，将SSD方法和HHT方法与其进行对比。

对仿真信号直接进行SSD，所得结果如图3 所示。由图可见，对仿真信号直接进行SSD 共得到5个SSC，这说明SSD 方法出现了过分解的现象，产生了冗余分量，而本文所提改进SSD方法准确分解出3个有效SSC，自适应剔除添加的随机噪声成分，且未分解出多余分量。对SSD 方法分解所得分量进行Teager 能量算子解调，得到的二维时频分布图如附录A 图A3所示。从图中的箭头指示可以看出，过分解现象的存在致使图中出现了干扰频率成分，对比图A2 可以发现原始SSD-Teager 时频分析方法的分析效果较本文所提改进SSD-Teager 时频分析方法差。

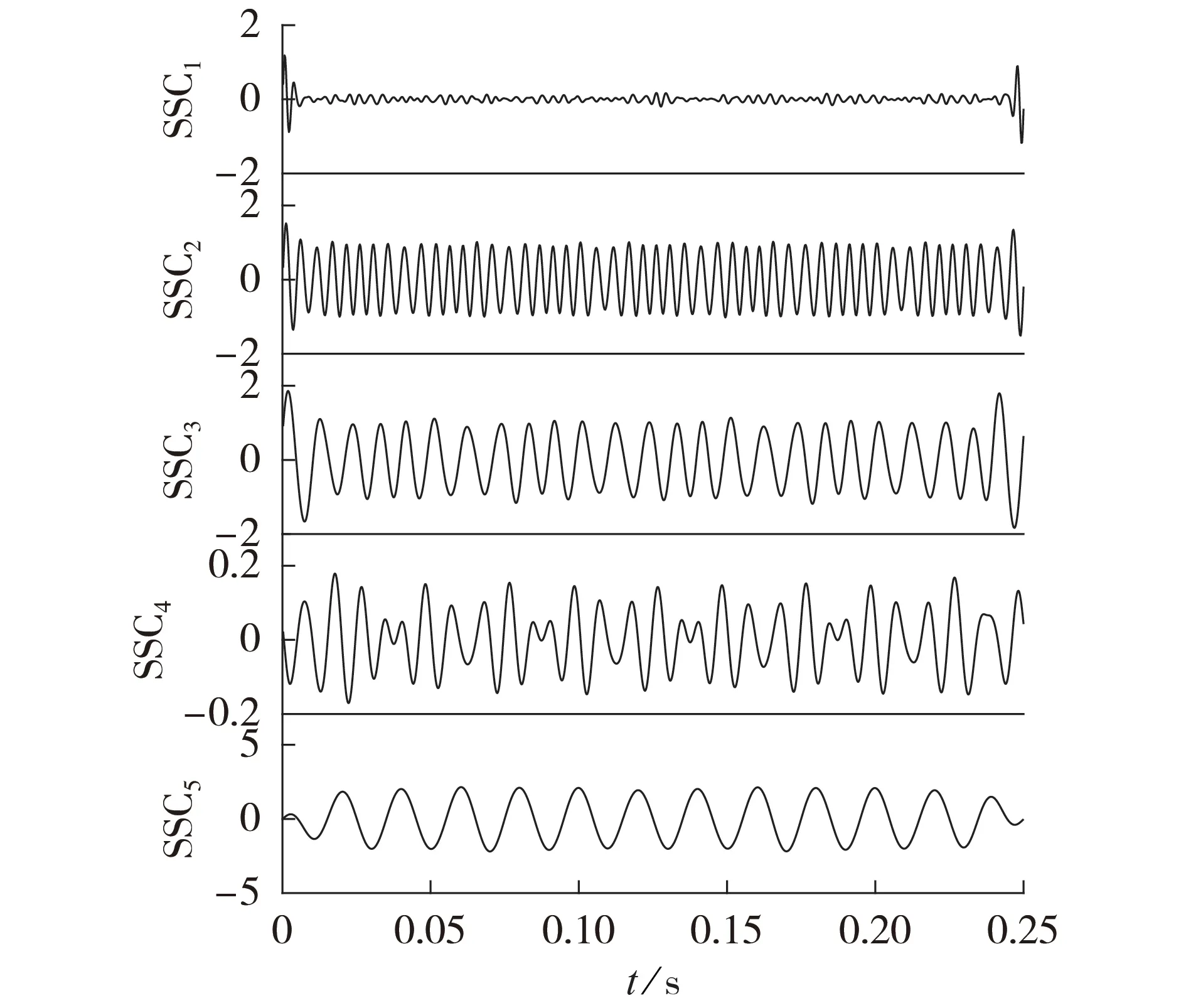
图3 仿真信号的SSD结果Fig.3 SSD result of simulated signal

利用HHT 方法对仿真信号进行处理，仿真信号经EMD 处理后共得到7 个IMF，如图4 所示。通过分 析 发 现IMF2、IMF3和IMF4这3 个 分 量 分 别 对 应x3(t)、x2(t)和x1(t)，但如图中虚线标记所示，IMF2—IMF4均出现了较大程度的模态混叠和幅值失真现象，IMF1、IMF5、IMF6和IMF7的存在表明出现了过分解现象。附录A 图A4 为对应的2 维时频分布图，由图可见由于EMD 方法的不足致使最终的时频分析结果较差。

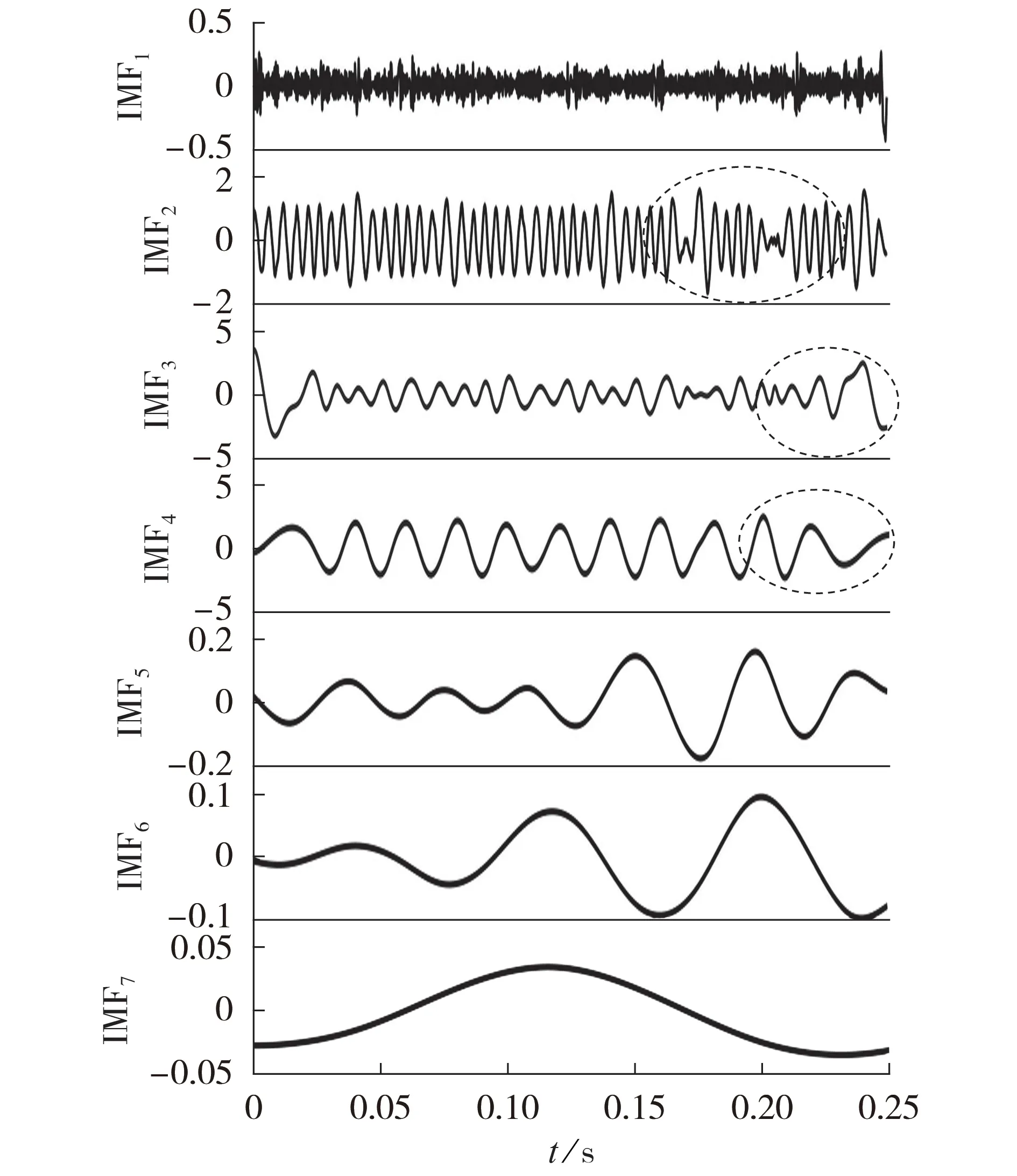
图4 仿真信号的EMD结果Fig.4 EMD result of simulated signal

3 工程案例分析

某电厂4 号机组配有2 台由成都风机厂生产制造的双级动叶可调轴流式引风机，该引风机型号为HU27050-22，主要由进气室、集流室、导叶、扩散器、动叶调节驱动装置、伺服驱动装置等部件组成，引风机水平布置，垂直进气、水平出气。引风机驱动装置为湘潭电机厂制造的YXKS1000-8 型电机，其额定功率为6 900 kW，额定转速为745 r／min。

电机-引风机轴系结构示意简图如图5 所示，其轴系共有1、2 号2 个单轴承用于支撑电机转子和1个3号组合轴承用于支撑引风机转子，2段轴系通过靠背轮由螺栓紧固。键相探头布置在电机侧靠背轮处，电机侧传感器布置在电机驱动端2 号轴承盖的水平和垂直方向上用于测量相应方向上的电机振动；引风机侧传感器布置在3 号轴承组前轴承位置，同样用于测量水平、垂直方向上的电机振动。本次振动测量所使用的传感器均在有效期内，并在使用前均校验合格，振动数据由合肥伟博测控科技有限公司生产的Vib900A 多通道现场振动信号采集系统采集。根据机组的历次启停机振动数据分析，在机组升降速过程中存在振动异常情况，采集时电机转速为480 r／min，采样频率设置为1 024 Hz，分析点数为2048。

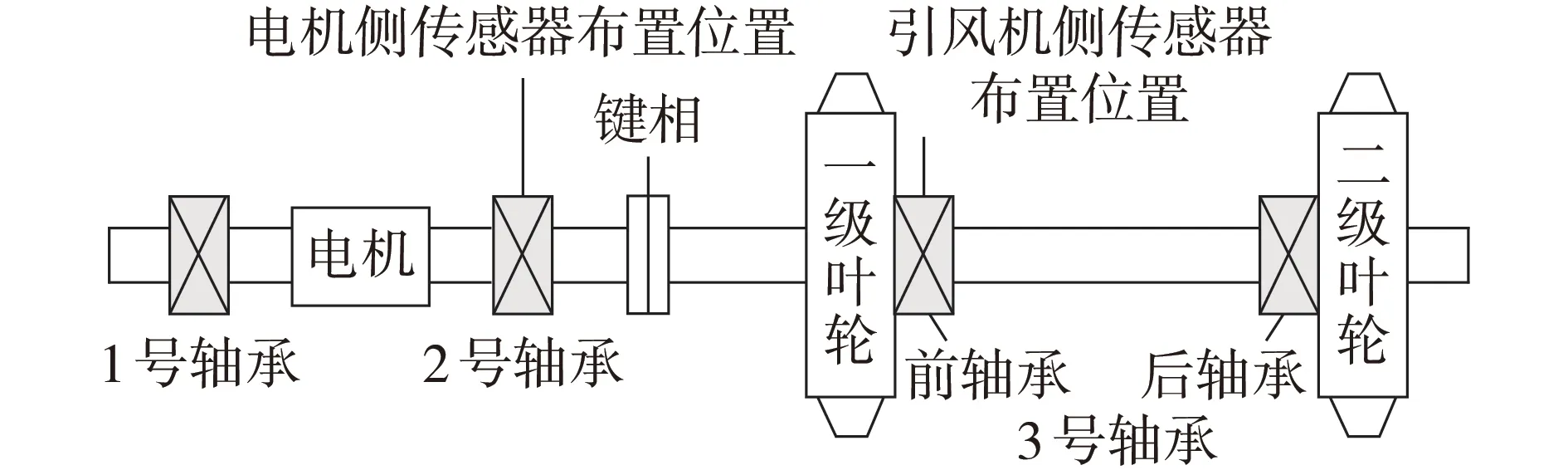
图5 轴系结构示意简图Fig.5 Simplified diagram of shafting structure

图6 为引风机侧水平、垂直方向上振动信号的时域波形图和频谱图，图7 为两方向振动信号合成的轴心轨迹图。由图可见，振动信号时域波形规律性明显，呈现出基频和二倍频成分叠加的“M”形波形，频谱图中存在基频和二倍频成分，轴心轨迹大致呈双环椭圆状，初步怀疑轴系存在不对中故障。

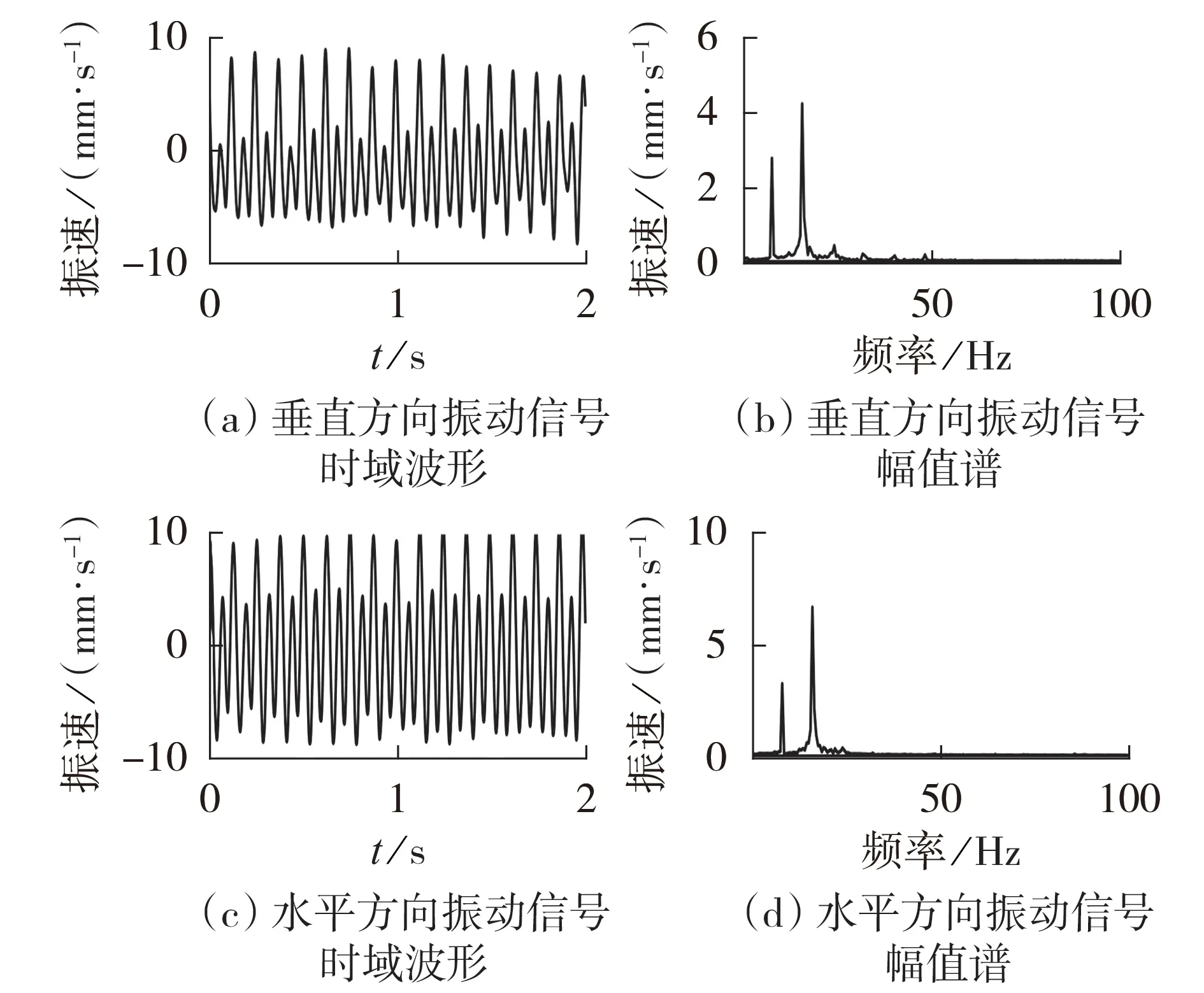
图6 原始振动信号的时域波形和频谱图Fig.6 Time-domain waveforms and spectra of original vibration signals

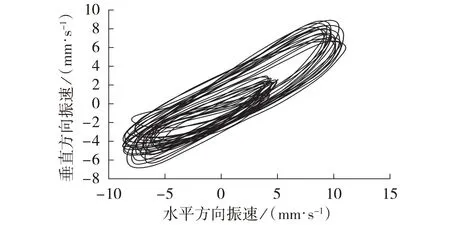
图7 轴心轨迹图Fig.7 Diagram of axis orbit

为进一步确定该引风机转子故障类型，利用本文所提方法进行进一步分析。垂直方向振动信号的改进SSD 结果如图8 所示，由图可见改进SSD 方法共得到4 个SSC。通过Teager 能量算子解调方法计算各个SSC的瞬时幅值及瞬时频率，汇总后得到的3维时频分布图如附录A 图A5 所示。4 个SSC 的瞬时频率分别为8、16、24、40 Hz，即分别对应基频、二倍频、三倍频以及五倍频分量，并且二倍频分量为主要分量，结合轴心轨迹呈双环椭圆以及二倍频能量明显超过基频能量等特征［23］可充分说明该引风机转子出现了不对中故障。

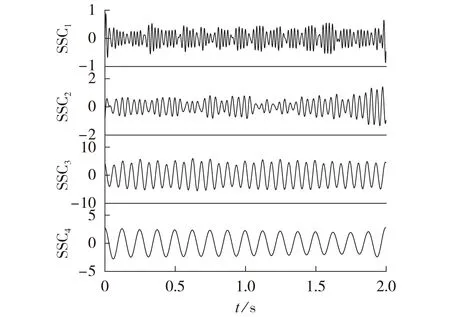
图8 实测信号的改进SSD结果Fig.8 Improved SSD result of measured signal

图9 为直接利用SSD 处理原始振动信号得到的分解结果，虽然也准确提取出了基频和二倍分量，但高频谐波分量（三倍频、五倍频分量）却没有被分解提取出来，出现了欠分解情况。通过Teager 能量算子解调计算2 个SSC 的瞬时幅值及瞬时频率，并汇总后得到3 维时频分布图如附录A 图A6 所示。2 个SSC 的瞬时频率分别为8 Hz 和16 Hz，即分别对应基频和二倍频成分，可见由于SSD 方法出现欠分解现象导致最终的时频分析效果较本文所提方法差。为进一步证明本文方法的优越性，将HHT 方法与本文方法进行对比分析。原始振动信号经EMD 处理所得结果如图10 所示。由图可见，EMD 共得到6 个IMF，其中IMF2对应工频成分，IMF1分量对应二倍频成分；由虚线标记处可以看出包含主要故障特征信号的2 个IMF 分量均出现了模态混叠和幅值失真现象。附录A 图A7 为对应的3 维时频图，由图可见，各IMF 分量频率调制现象明显，频率成分杂乱无章无法准确识别具体频率信息，HHT 方法的时频分析效果明显较本文方法差。

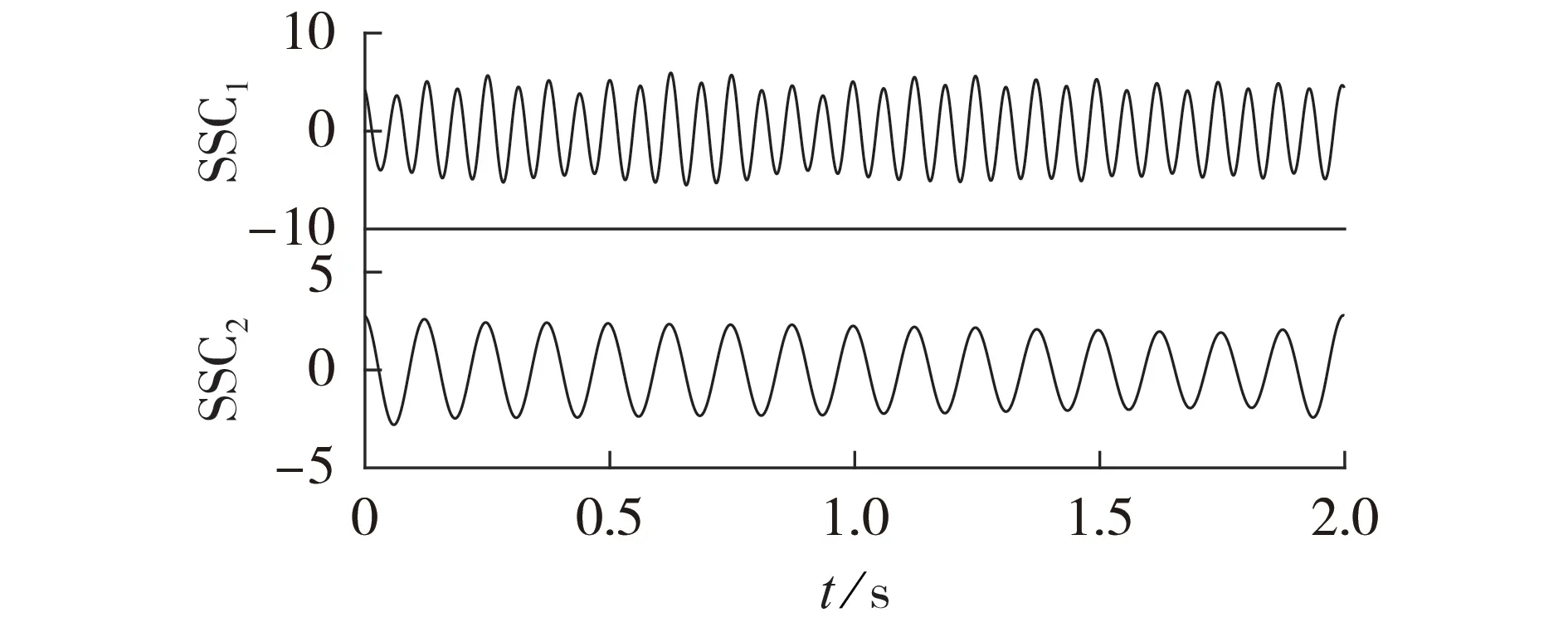
图9 实测信号的SSD结果Fig.9 SSD result of measured signal

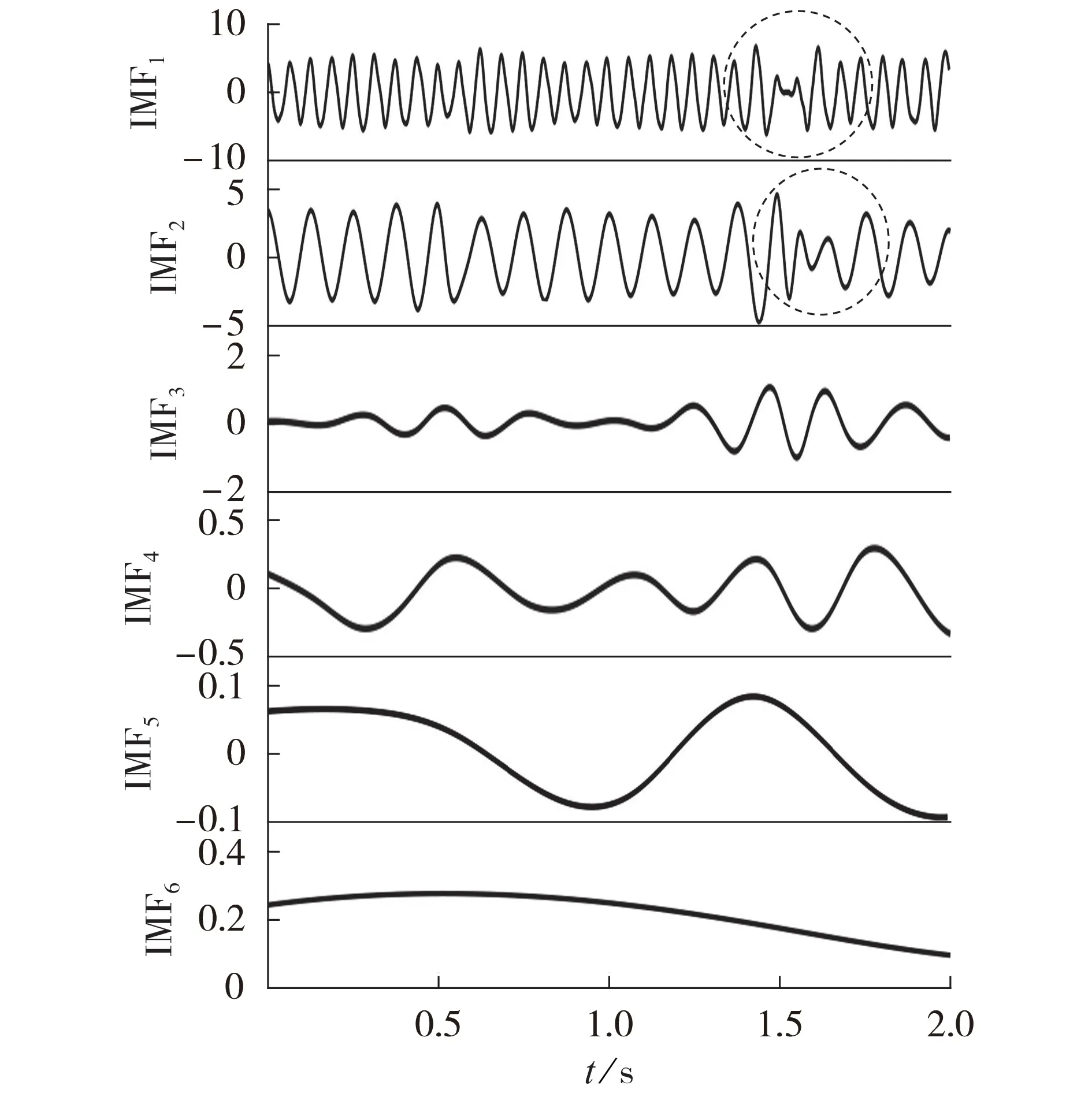
图10 实测信号的EMD结果Fig.10 EMD result of measured signal

4 结论

本文结合SSD 方法和Teager 能量算子解调各自的优点，提出了一种改进SSD-Teager 时频分析的引风机转子故障诊断方法。针对SSD 方法以能量比作为迭代停止条件导致鲁棒性欠佳的缺点，本文融合互信息判据对循环迭代过程进行协同控制，从而自动确定SSC 数量，实现信号自适应处理过程。利用改进SSD 方法对原始振动信号进行自适应分解得到一系列SSC，再融合Teager 能量算子解调求取各分量的瞬时振幅和瞬时频率信息，最后根据时频特征判别故障类型。将改进SSD-Teager时频分析方法应用于现场实测引风机转子不对中故障振动信号分析，最终准确地识别出转子故障状态，并且与传统HHT 方法相比优势明显。综上所述本文方法具有一定工程实际应用价值，可为类似旋转机械故障损伤判定提供参考借鉴。

附录见本刊网络版（http：//www.epae.cn）。