基于后验分布信息的SSAE暂态稳定评估模型倾向性修正方法
2022-03-17王怀远陈启凡
林 楠,王怀远,陈启凡
(福州大学 电气工程与自动化学院 智能配电网装备福建省高校工程研究中心,福建 福州 350116)
0 引言
近年来,随着交直流混联电网的形成、电力电子设备的增加和电力市场的推广运行,电力系统的复杂程度进一步增加,电力系统暂态稳定性评估的难度也随之增大[1-2]。传统的暂态稳定评估方法有时域仿真法和直接法。时域仿真法根据给定的电力系统拓扑结构和运行条件进行仿真计算,具有精度高的特点,但其耗时长,无法实现在线计算的功能。直接法通过建立一个特定的“能量函数”来反映系统特性,然而对于复杂的电力系统,很难找到与其对应的函数实现暂态稳定评估。因此,传统的暂态稳定评估方法具有一定的局限性,亟需研究一种新的方法实现暂态稳定的在线评估。
智能电网的发展使得人们储存了大量的电力系统数据信息,而电力系统大数据和人工智能的发展又使得机器学习在暂态稳定评估中的应用成为可能。机器学习通过对大量电力系统故障样本的训练,提取出样本与稳定性之间深层次的关系,其具有精确度高、计算速度快等优点。深度学习作为机器学习的重要领域,具有浅层学习所不具备的数据挖掘能力。常用的深度学习模型有卷积神经网络[3]、深度置信网络[4]、堆叠自动编码器[5-6]和长短期记忆(LSTM)神经网络[7-8]等。文献[8]采用LSTM 神经网络对系统的时序样本进行在线暂态稳定评估,提出一种时间自适应方案以提高评估速度和精度。文献[9]提出基于深度置信网络的暂态稳定评估方法,使用大量无标签样本来提高模型的准确率。文献[10]采用堆叠降噪自动编码器和支持向量机相结合的集成模型,提高暂态稳定预测的准确率,并对运行方式的危险程度进行分级处理。文献[11]提出在稳定样本与不稳定样本数量差别很大的情况下,采用改进的对抗神经网络加强对不稳定样本进行学习的方法,以此提高暂态稳定评估的正确率。
样本数据是机器学习模型训练的基础,样本数据的不平衡会影响模型的性能。在模型训练过程中,数量较多类型样本对模型参数进行调整的频率要高于数量较少类型样本,导致最终生成的评估模型对于数量较多类型样本的拟合程度高于数量较少类型样本。因此当训练样本中的稳定样本与不稳定样本数量差别较大时,会造成模型在暂态评估过程中带有一定的评估倾向性,从而导致暂态稳定评估的正确率降低。
目前,主要是从数据层面和算法层面对数据不平衡问题进行处理。数据层面的处理方法主要是借助样本数量的调整使整体训练集样本趋于平衡,包括欠采样[12]和过采样[13]。欠采样方法会损失大量样本信息数据,而过采样方法容易造成过拟合问题。算法层面的处理方法主要是集成学习法[14]和代价敏感法[15-17]。集成学习法往往结合采样法训练多个弱分类器,将多个弱分类器组合得到具有较高精度的融合模型,但分类器在训练过程中极易受到噪声数据和离群数据的干扰。代价敏感法通过制定代价敏感矩阵来调整错分权重,可以有效缓解样本不平衡带来的问题。但目前的数据不平衡处理方法主要是从样本的先验分布信息出发,利用样本数量的比值对模型的评估倾向性进行修正,忽略了训练样本的空间分布不同所带来的不平衡问题。
对于样本不平衡现象引起的暂态稳定评估倾向性问题,本文提出基于样本后验分布信息的代价敏感修正方法。通过仿真分析发现,训练后模型的损失函数均值能够在一定程度上反映模型对样本的拟合程度,因此基于该后验分布信息引入代价敏感系数,从而改善模型的性能。本文基于堆叠稀疏自动编码器SSAE(Stacked Sparse AutoEncoder)[18]构建暂态稳定评估模型,通过稀疏化提高模型的泛化能力,减小数量较多类型样本过拟合问题的影响。本文方法能够有效修正电力系统暂态稳定评估中不平衡样本带来的评估倾向性问题,提高模型的全局准确率。
1 SSAE原理
电力系统暂态稳定评估可以看作是一个模式识别问题。模型评估倾向性问题是样本不平衡现象和样本过拟合共同作用的结果。评估倾向性的本质是模型对于多数的稳定样本产生了过拟合。稀疏化方法能有效减小过拟合问题的影响,使得模型的训练过程更加稳定。因此,本文基于SSAE构建暂态稳定评估分类器,以学习电力系统故障前后的动态响应信息和故障后暂态稳定状态之间的映射关系[18]。
1.1 稀疏自动编码器
稀疏自动编码器(SAE)在自动编码器的基础上加入稀疏约束,从而对原始输入信息进行压缩,剔除与暂态稳定评估无关的冗余信息。
SAE 的训练由编码sf和解码sg这2 个过程组成[18],分别如式(1)和式(2)所示。
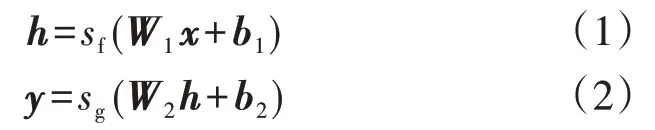
式中:h为隐含层输出向量;x为输入数据;y为输出数据;W1和W2为权重向量;b1和b2为偏置向量。
SAE 的训练目标是使解码后的特征与输入编码器的暂态稳定特征尽可能相同,即最小化式(3)。

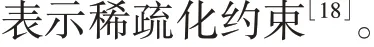
1.2 SSAE
SSAE 是由多个SAE 的编码器依次堆叠,并在最后加入一层逻辑分类器的深度网络模型。电力系统的动态响应信息通过输出层输入评估模型后,经过SSAE 逐层进行特征提取,最终通过逻辑分类器输出暂态稳定评估结果。
SSAE 的训练过程由预训练和微调2 个阶段组成。首先,依次训练每个SAE,该过程无需暂态稳定状态标签的参与,为无监督学习过程;然后,将预训练得到的当前SAE编码器的输出作为下一个SAE的输入,当所有SAE预训练完成后,将所有的编码器依次堆叠进行特征提取,并通过逻辑分类器输出暂态稳定评估结果;最后,通过反向传播法对整个评估模型参数进行微调,在微调过程中,训练的目标是最小化评估的暂态稳定状态与真实的暂态稳定状态间的误差,评估误差LSSAE的计算公式如式(4)所示。
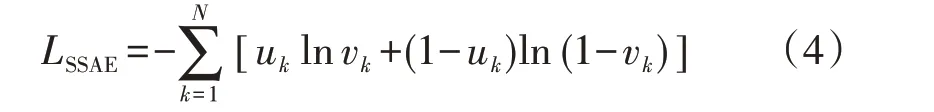
式中:uk为第k个样本的真实暂态稳定状态标签;vk为第k个样本的暂态稳定评估结果标签。
2 不平衡样本的处理算法
2.1 样本不平衡对评估结果的影响
在模型训练过程中,样本的评估误差会对模型参数进行修正。如果训练样本中各类样本的分布不同,则会导致各类样本对模型的修正程度不同。在对临界样本进行评估时,对稳定样本拟合程度更高的评估模型倾向于将临界样本评估为稳定,从而影响模型的整体性能。在电力系统中,实际的稳定样本数量远多于不稳定样本数量,若采用这样的样本集训练模型,训练过程中稳定样本被评估错误的次数会多于不稳定样本,模型参数被稳定样本修正的次数也相对更多,因此模型对稳定样本的拟合程度更高。此外,对于同类的暂态稳定评估样本,样本对应的电力系统故障的严重程度不同,则其对评估模型的影响也不同。当样本对应的故障持续时间远小于或远大于其临界清除时间时,评估误差较小,在训练过程中对模型的影响也较小;而当样本对应的故障持续时间接近临界清除时间时,评估误差较大,在训练过程中对模型的影响也较大。因此,电力系统暂态稳定评估中的样本不平衡问题是由样本数量不平衡和样本故障严重程度分布不平衡共同导致的。
在电力系统中,根据式(5)中的暂态稳定裕度指标ζ将所有的样本分为稳定样本与不稳定样本。

式中:δ为任意2 台机组间的最大功角差。当ζ>0时,样本为稳定样本,标签为1;否则,样本为不稳定样本,标签为0。
定义λ表示训练集中不稳定样本数量Nu与稳定样本数量Ns的比值:

为了验证样本不平衡程度对评估结果的影响,采用基于SSAE 的暂态稳定评估模型,在IEEE 39 节点系统进行测试,结果如表1所示。表中:PA为模型的总体准确率;PFU为不稳定样本的评估错误率;PFS为稳定样本的评估错误率。PA、PFU、PFS均为模型的评价指标,定义分别如式(7)—(9)所示。
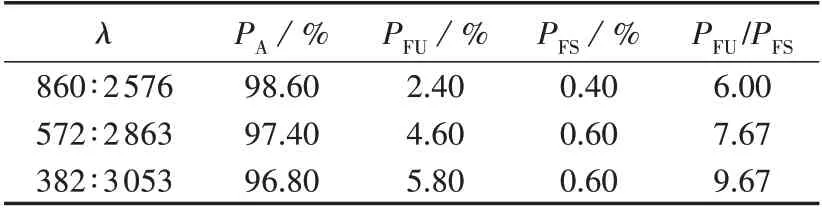
表1 IEEE 39节点系统的暂态稳定评估结果Table 1 Transient stability assessment results for IEEE 39-bus system
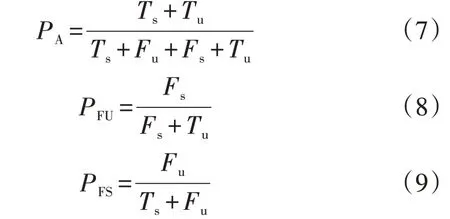
式中:Ts为预测标签为稳定的样本中预测正确的数量;Tu为预测标签为不稳定的样本中预测正确的数量;Fs为预测标签为稳定的样本中预测错误的数量;Fu为预测标签为不稳定的样本中预测错误的数量。
由表1 可知:随着λ值的减小,模型的总体正确率逐步降低,不稳定样本的评估错误率逐渐增加;随着λ值由860∶2 576 下降到382∶3 053,PFU/PFS由6.00增加到9.67,模型的评估倾向性越来越强。
在电力系统暂态稳定评估中,存在不稳定样本数量远少于稳定样本数量的样本不平衡现象。对于二分类样本不平衡问题,根据贝叶斯公式,对于样本a属于第θ类的后验概率p(θ|a)为:

在暂态稳定评估中,判别样本为稳定标签1 和不稳定标签0 的后验概率分别如式(11)和式(12)所示。
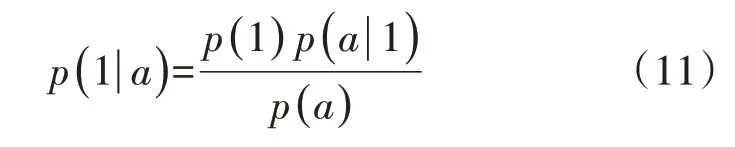
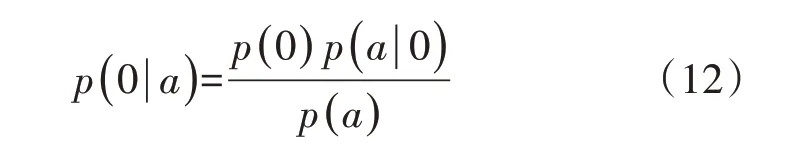
由此,可以用式(13)反映数据的不平衡情况。

本文对使用基于数量比γ的修正方法进行测试[20],结果如表2所示。
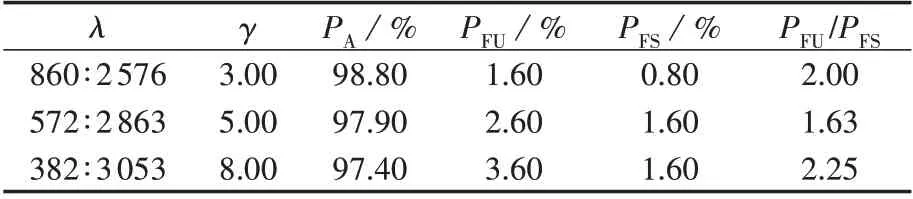
表2 基于数量比γ的代价敏感修正方法Table 2 Cost-sensitive correction method based on quantity ratio γ
由表2 可知,稳定样本的评估错误率与不稳定样本的评估错误率比值PFU/PFS相较于表1 有所改善,因此基于先验分布的代价敏感法在一定程度上改善了评估结果的倾向性。但稳定样本的评估错误率与不稳定样本的评估错误率依然相差较大,修正效果并不理想,这是由于基于先验分布的代价敏感法只考虑了样本的数量不平衡,而忽略了暂态稳定评估样本故障严重程度分布不平衡的情况,样本的数量信息并不能准确地反映不平衡样本对模型的影响,因此,本文提出一种基于样本后验信息的样本不平衡处理方法,对电力系统暂态稳定评估中的倾向性进行修正。
2.2 基于后验分布信息的不平衡数据处理算法
用训练样本对模型进行预先训练可得到样本的后验分布信息。样本的后验分布信息同时考虑了样本的数量和空间分布情况等对评估模型参数的影响,能更确切地反映样本的不平衡情况。对于机器学习模型,训练后模型各类样本的损失函数值能体现样本的后验分布信息,各类样本的损失函数均值在一定程度上反映了评估模型对各类样本的拟合程度。
训练集的稳定样本和不稳定样本的损失函数均值Rs、Ru分别如式(15)、(16)所示。
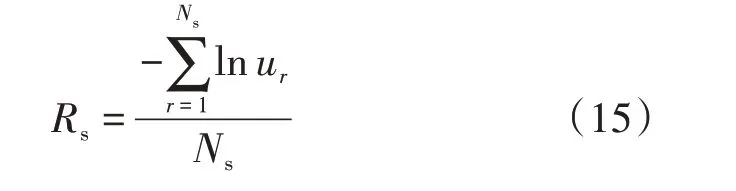
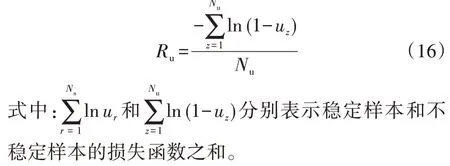
训练集样本的损失函数均值反映样本的后验分布情况。某类样本的损失函数均值越小,评估模型对该类样本的拟合程度越高。相较于先验信息,样本的后验信息能更准确地反映样本的分布情况。因此,训练后模型的评估倾向性可以通过不稳定样本和稳定样本的损失函数均值之比Rimb来衡量,如式(17)所示。

当Rimb=1 时,模型对稳定样本和不稳定样本的拟合程度相同或相近,模型不存在评估倾向性问题;当Rimb≠1 时,评估模型对稳定样本和不稳定样本的拟合程度不同,Rimb的数值反映了模型的评估倾向性。
在IEEE 39 节点系统上测试不同λ值下的Rimb变化情况,结果如图1所示,图中Rimb为标幺值。
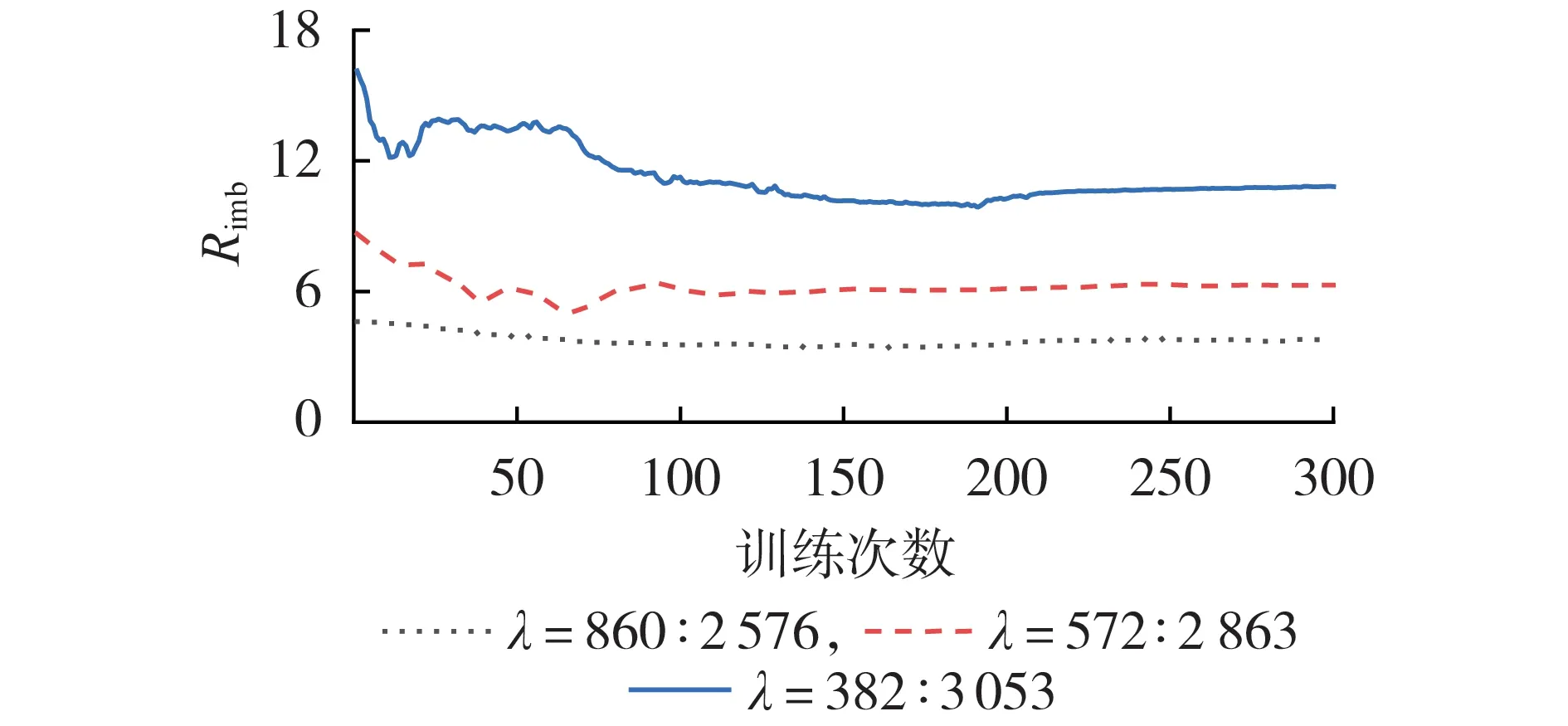
图1 不同λ值下的Rimb变化情况Fig.1 Variation condition of Rimb under different values of λ
由图1 可知:随着训练次数的不断增加,Rimb逐渐趋近于一个稳定的常数值,在不同的λ值下,Rimb趋近于不同的稳定常数值;随着不平衡程度的增大,Rimb越来越偏离常数1,这表明在一定的训练次数之后,评估模型的训练基本完成了对2 类样本的拟合,而该常数值反映了模型对2 类样本的拟合程度。因此,本文提出利用Rimb来评估训练样本的不平衡程度,同时将其引入式(4)作为损失函数的修正系数以修正模型的倾向性,如式(18)所示。

当原模型倾向于将样本评估为稳定时,Rimb>1,此时,对于相同的预测值,不稳定样本的损失函数值将被放大,从而增大了因不稳定样本评估误差而产生的模型参数调整量,实现了调整模型评估倾向性的目的。
2.3 应用过程
本文提出的暂态模型评估过程具体流程如下。
1)对于离线训练部分,用历史数据和离线仿真生成训练集,对基于SSAE的暂态稳定评估模型进行训练。每个训练样本需要包含故障发生前、故障发生时、故障发生后0.1 s的系统运行信息。
2)对基于SSAE 的暂态稳定评估模型进行初次训练,根据式(15)—(17)计算模型训练过程中的Rimb。
3)将稳定后的Rimb作为损失函数的修正系数,构建式(18)所示新的损失函数,并对基于SSAE的暂态稳定评估模型进行重新训练。
4)对于在线评估部分,将离线训练好的SSAE评估模型配置在控制中心,通过广域测量系统得到电力系统实时响应数据。当达到故障清除后0.1 s 时,将采集到的特征量输入训练好的SSAE模型,评估模型通过学习到的固定映射关系迅速输出暂态稳定性的评估结果。
3 算例分析
3.1 样本集的构造
本文以IEEE 39 节点系统作为测试系统,在该系统上对12 375 种故障情况进行仿真,共生成7 010例稳定样本和5 365 例不稳定样本。系统的运行状态包括系统容量的90%、95%、100%、105%、110%这5 种负荷水平。故障发生地点分别位于线路全长的10%、50%、90%处,故障类型为永久性三相短路,故障持续时间为0.1~0.3 s。最长仿真时间为4 s,采样频率为每秒120次。
选择故障发生瞬间前一采样周期、故障发生瞬间后一采样周期、故障清除瞬间前一采样周期、故障清除瞬间后一采样周期和故障清除后0.1 s 各台发电机的功角、角速度与不平衡功率作为原始特征。
3.2 实验结果分析
本文以SSAE为例建立暂态稳定评估模型。SSAE的参数如下:隐含层神经元数量分别为100、50、25个;预训练100次;微调200次;α=0.001,β=0.0001。
本次测试从12375个数据中随机抽样选取训练样本数量3 435 个以及测试样本数量1 000 个。训练集中不稳定样本数量与稳定样本数量的比值分别设置为860∶2576、572∶2863、382∶3053,测试集中不稳定样本数量与稳定样本数量的比值均为500∶500。
3.2.1 不同修正方法的修正效果
本文以SSAE分类器为基础,对比几种常用的数据不平衡处理方法,包括过采样方法中的自适应综合 过 采 样ADASYN[21](ADAptive SYNthetic sampling)和合成少类过采样SMOTE[22](Synthetic Minority Oversampling TEchnique)、随机欠采样方法、基于先验分布的传统代价敏感法以及本文基于后验分布的代价敏感法。为了增强对比结果的可靠性,所有方法均进行3次随机实验,将3次实验结果的平均值作为最终的结果,如表3所示。
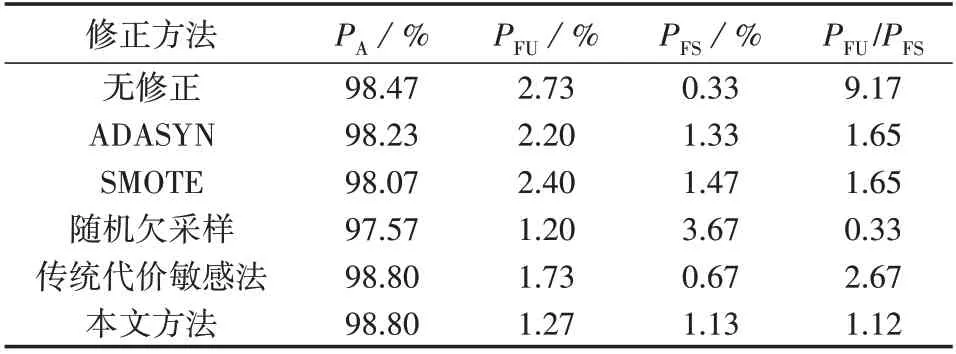
表3 在训练集中λ=860∶2576下不同修正方法的测试结果Table 3 Test results of different correction methods with λ=860∶2576 in test set
表3中的ADASYN、SMOTE 属于过采样方法,其通过线性插值生成不稳定样本,使得不稳定样本的数量增加到与稳定样本的数量相等。然而,ADASYN易受离群值的影响,而SMOTE 则是随机生成样本。这2 种过采样方法生成的样本不尽合理,虽然在一定程度上修正了评估倾向性,但模型的总体准确率略有下降,其误判数量相较于无修正模型的误判数量分别增加16%和26%。随机欠采样方法随机剔除部分稳定样本,使得2 类样本数量相等,该方法会丢失大量稳定样本信息,导致过拟合问题,其误判数量相较于无修正方法增加59%。传统代价敏感法相较于采样法的全局准确率有所提高,但模型评估倾向性问题依然存在。本文方法通过样本的后验分布信息度量样本的数量不平衡和分布不平衡,修正后不稳定样本的评估错误率和稳定样本的评估错误率之比最接近1,具有最高的全局正确率。同时,本文方法不需要丢失真实数据或生成虚假数据,相较于采样法不会增加算法的复杂性和训练难度。
3.2.2 不同样本比例下的修正效果
由3.2.1 节中的结果可知,采样法在处理不平衡样本时的效果并不理想,因此本节着重对传统代价敏感法和本文方法进行进一步对比,测试不同λ值下的评估结果,如表4和表5所示。
由表4 和表5 可知:随着样本不平衡程度的增大,本文方法依然能够很好地改善评估模型的倾向性;在2 种情况的测试中,本文方法的全局准确率均为最高,而不稳定样本的错误率均为最低,且不稳定样本的错误率和稳定样本的错误率之比最接近1。因此,基于后验分布信息的修正方法在实现良好的评估倾向性修正效果的同时,能有效提高模型的全局准确率。
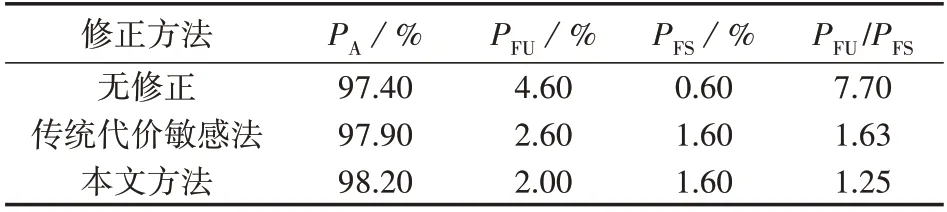
表4 在训练集中λ=572∶2863下不同修正方法的测试结果Table 4 Test results of different correction methods with λ=572∶2863 in test set
3.2.3 不同稀疏化程度下的修正效果
稀疏化后的评估模型对于数据具有更好的泛化性能,降低了模型的过拟合程度。本文在训练集中λ=382∶3 053 的情况下对不同稀疏化程度的模型进行测试,结果如表6所示。
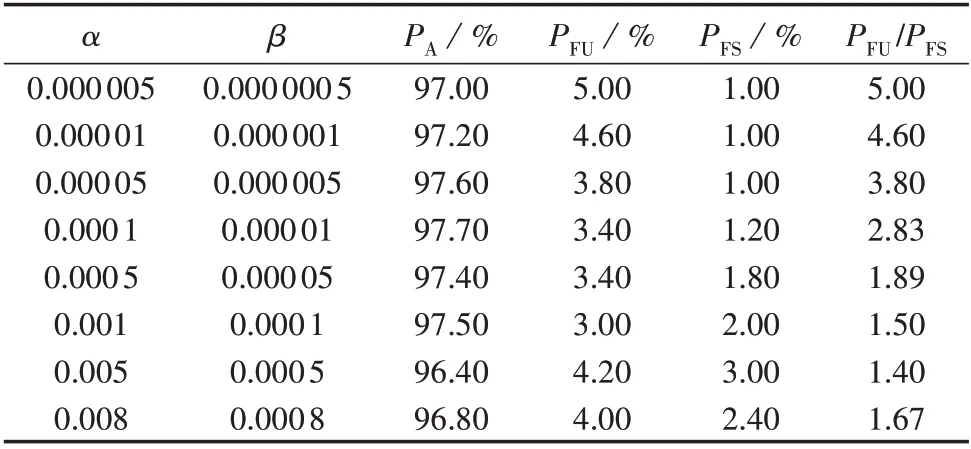
表6 不同稀疏化程度下的测试结果Table 6 Test results under different sparseness degrees
由表6可知:α和β越大,稀疏化程度越高;随着稀疏化程度的不断提高,模型对稳定样本的过拟合程度逐渐降低,模型倾向性问题得到改善,模型的全局准确率得到提高,当达到某一稀疏化程度时,模型的评估性能开始逐渐下降。因此,稀疏化方法的引入,能够通过遏制数量较多类型样本的过拟合程度来提高模型的性能。
3.2.4 大规模电力系统的测试结果
为了验证本文方法的实用性,在华东某区域系统中对本文方法的效果进行测试。测试系统包括6 040 条母线和5 599 条输电线路;相量测量单元(PMU)被配置在426 台容量大于200 MW 的发电机上;系统频率为50 Hz;负荷水平为系统容量的100%;故障发生在500 kV 及以上电压等级的输电线路全长的10%、50%和90%处;故障类型为N-1三相短路、N-2三相短路和两相接地短路;故障持续时间为0.1~0.4 s。从生成的样本中随机抽取训练样本30 015 例(不稳定样本2 729 例,稳定样本27 286例)和测试样本3 000 例(不稳定样本1 500 例,稳定样本1500例)。
SSAE的隐含层神经元数量分别为512、256、128个;预训练100次;微调500次;α=0.0001,β=0.00001。训练集中不稳定样本数量与稳定样本数量的比值设置为λ=2 729∶27 286,在该系统下本文方法测试结果如表7所示。
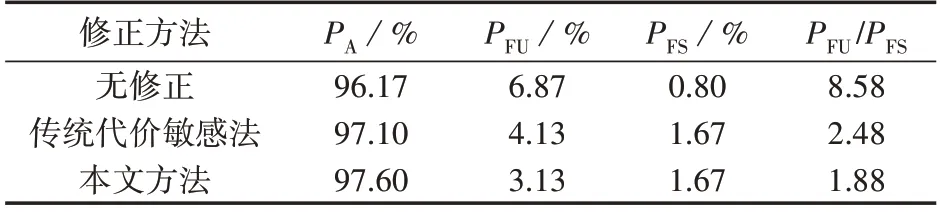
表7 大规模系统下不同修正方法的测试结果Table 7 Test results of different correction methods in large-scale system
基于后验分布信息确定的修正系数Rimb=17.5,约为训练集中不稳定样本数量与稳定样本数量比值的1.75倍。由此可见,在大规模系统下,除了样本数量不平衡外,样本分布的不平衡对评估倾向性有重大影响。相较于传统代价敏感法,本文方法同时考虑了样本数量不平衡和分布不平衡,即使在大规模系统下也能实现更好的不平衡修正效果,有效提高模型的评估正确率。
基于GTX1080Ti GPU 和i7 7700 CPU,对本文方法在大规模系统中的训练时间和评估速度进行测试,得到训练时间为990.40 s,基于SSAE的暂态稳定评估模型评估时间为0.87 ms。
值得一提的是,实际电力系统中存在许多不会失稳的故障情况,即在较长的故障持续时间下,某些故障依然不会使得系统失去暂态稳定。这些非常稳定的样本不仅几乎不会帮助深度学习模型学习到合理的评估规则,而且会导致严重的样本不平衡问题。因此,将这些非常稳定的故障样本从训练集中去除,既能减轻样本不平衡程度,又能提高模型的训练效率。
此外,为了应对系统运行方式变化等导致的网络拓扑结构改变,利用迁移学习[23]、周期性更新[20]等方法能够有效提高评估模型在大规模系统中的适应能力。
4 结论
本文根据稳定样本与不稳定样本的损失函数均值比,提出一种量化样本不平衡程度的方法。基于样本的不平衡程度指标,结合代价敏感法修正模型的损失函数,以此改善模型经不平衡样本训练的评估倾向性问题。在IEEE 39 节点系统和华东某区域系统进行仿真测试,对于不同的不平衡样本集,本文方法均能够有效改善模型的评估倾向性问题,同时,模型的全局准确率也得到一定程度的提高。
稀疏化方法的引入,减小了模型对数量较多类型样本的过拟合程度,提高了评估模型的泛化能力。测试结果表明,适当的稀疏化程度可以有效降低模型的过拟合程度,进而改善模型的倾向性问题。
