基于R藤Copula-DBN时空相关性建模的风光荷功率概率预测
2022-03-17廖芷燕李银红
廖芷燕,李银红
(华中科技大学 电气与电子工程学院,湖北 武汉 430074)
0 引言
可再生能源具有随机性、间歇性和不确定性问题,其并网规模的不断增大,给电力系统带来了很大的不确定性,同时增加了电力系统负荷的随机波动性,对电力系统的安全稳定和经济运行造成了威胁,因此,针对不确定性建模的风光荷功率概率预测对保障电力系统安全稳定和经济运行具有重要的实用价值和意义[1]。
不确定性建模是风光荷功率概率预测的核心,目前主要为考虑多元随机变量相关性的不确定性建模,建模方法包括统计学方法和人工智能方法。统计学方法可分为Pearson相关系数[2]、秩相关系数[3]、贝叶斯网络[4]和Copula 函数[5]等。其中,Pearson 相关系数只能研究变量之间的线性相关程度,不能分析风-光-荷之间复杂的非线性相关性;秩相关系数如Kendall秩相关系数和Spearman秩相关系数,能够较好地描述风电出力相关性的非线性特征,但难以准确度量风电出力在极小和极大情况下的尾部相关性;基于数据挖掘的贝叶斯网络模型可以很好地描述风-光-荷之间的复杂相关性[4],但在面对高维数据时因需要搜索的有向无环图空间急剧增大,在此巨大空间中采用一般的方法搜索最优的贝叶斯网络结构变得相当困难,存在计算量较大、时间成本较高以及有效性较差等方面的问题。
Copula 函数由于具有能够刻画变量间的非线性相关性、易于构造联合分布模型的独特优势,近年来也被引入风光荷功率相关性分析中[5]。在高维背景下,非参数R 藤Copula 模型[6]通过一定规则的拓扑结构刻画多维变量之间的复杂相关性,刻画效果优于C 藤和D 藤,但高维时该模型需逐层优化求解参数,计算量巨大。文献[7]结合藤Copula模型与贝叶斯网络分析变量间的相关性,模型效果优于朴素贝叶斯模型,但该研究未与现有贝叶斯网络结构学习方法进行对比,且仅采用相关性较大的变量进行建模,相关性刻画不够全面。
人工智能方法中:人工神经网络ANN(Artificial Neural Network)[8]和支持向量机回归SVR(Support Vector Regression)[9]通过大量历史数据建立变量间的非线性关系,将动态时间建模问题变为静态空间建模问题,难以描述时间序列的自相关性,预测精度有限[10];长短期记忆LSTM(Long Short-Term Memory)神经网络[10]可全面完整地描述时间序列的自相关性,对时序数据有较好的预测精度,但所建立的模型复杂、训练难度大;深度置信网络可提高预测精度,但弱化了时间序列的自相关性[11]。
综上所述,目前多维风光荷功率概率预测的难点在于兼顾以下2个方面的要求[1]:一是综合考虑时空相关性;二是保证计算精度和计算效率。为综合分析多维风光荷时空相关性,本文提出一种基于R藤Copula-动态贝叶斯网络DBN(Dynamic Bayesian Network)的时空相关性建模方法。该方法能够弥补现有空间相关性建模方法模型复杂和准确性较低的不足,并利用DBN 在时间点序列上特有的相依结构分析风光荷时间自相关性,可较为全面完整地描述时间序列的自相关性,该方法具有较高的计算精度和计算效率。首先,采用非参数核密度估计KDE(Kernel Density Estimation)确定二元Copula 函数的概率密度,通过Kendall 秩相关系数确定R 藤Copula模型的最优树结构;然后,以最优树结构的第一层作为贝叶斯网络结构,结合传递熵确定网络结构中各变量之间的相互依存关系,即R 藤Copula 贝叶斯模型,刻画多维风光荷功率的空间相关性,并考虑风光荷功率均为时序变量,相邻时刻风光荷功率数据存在一定的时间自相关性,将所提R 藤Copula 贝叶斯模型扩展到时域,建立R藤Copula动态贝叶斯模型,以综合分析风光荷时空相关性;最后,对含4 座风电场、9座光伏电场及3个地区负荷的RTS96节点系统进行计及时空相关性的多维风光荷功率概率预测,验证所提方法的有效性。
1 DBN
1.1 基于DBN的相关性分析
DBN能够学习变量间的概率依存关系及其随时间变化的规律,是传统的静态贝叶斯网络在时间点序列上的延拓[12],由初始网络B0和转移网B→组成。初始网络B0通过有向无环图描述网络中各个节点变量之间的概率依存关系,转移网B→则通过网络拓扑结构反映变量之间的概率依存关系及其随时间变化的情况,因此,DBN不但能够对变量所对应的不同特征之间的依存关系进行概率建模,而且也能很好地反映特征自身的时序关系,常被用于描述随机变量的时间自相关性及空间相关性。

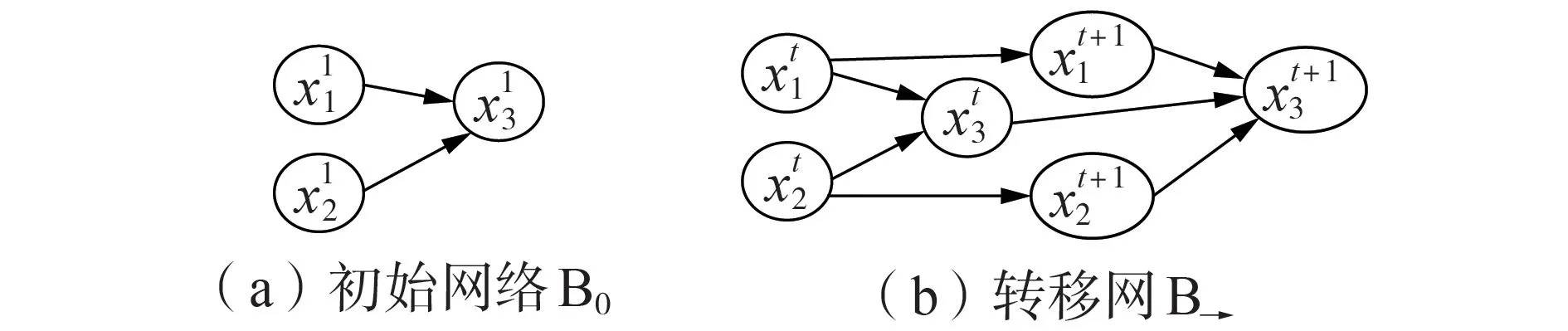
图1 DBN实例Fig.1 Instance of DBN
DBN对变量时间自相关性的描述通过变量在时刻t=1,2,…,T(T为最大时刻)上的联合概率分布体现:
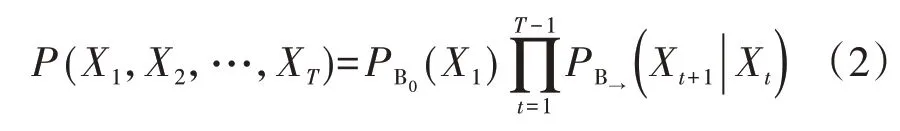
式中:PB0(X1)为t=1 时刻的状态量集合的联合概率分布;PB→(Xt+1|Xt)为t时刻状态量集合为Xt时t+1时刻状态量集合Xt+1的条件概率分布,不同时刻PB→(Xt+1|Xt)的大小描述了变量集合在不同相邻时刻下时间自相关性的强弱。
1.2 初始网络B0的建立
初始网络B0的建立是DBN 建模的核心。传统的初始网络B0结构学习方法中:基于评分搜索的K2 算法[4]需要利用先验信息,适用场景较少;马尔科夫链蒙特卡洛MCMC(Markov Chain Monte Carlo)算法[13]虽能保证算法的学习精度,但收敛速度慢;爬山HC(Hill Climbing)算法[14]实现简单,但不一定能搜索到全局最优解;最大最小爬山MMHC(Max-Min Hill Climbing)算法构建的网络质量高,但容易陷入局部最优[15]。此外,高维时上述方法的计算开销大,时间成本高且有效性较差,因此,亟需对高维背景下初始网络的结构学习方法进行研究。
2 藤Copula模型
2.1 Copula函数
Copula 函数可将随机变量的边缘分布与相关性分开表达,易于描述随机变量间的复杂相关性[16]。若F(x1,x2,…,xn)是具有连续边缘分布的随机变量x1、x2、…、xn的联合概率分布函数,则存在唯一的Copula函数C(u1,u2,…,un)满足[5]:
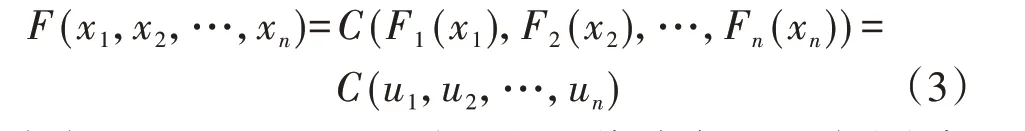
式中:ui=Fi(xi),Fi(xi)为xi的边缘分布。对式(3)求导,可得多元随机变量的联合概率密度函数f(x1,x2,…,xn)为:
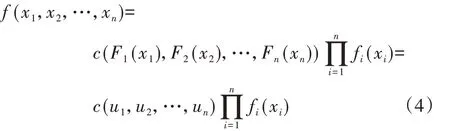
式中:fi(xi)为Fi(xi)的导数;c(u1,u2,…,un)为Copula函数C(u1,u2,…,un)的导数,如式(5)所示。
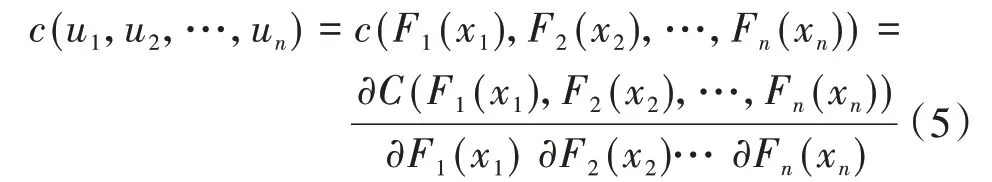
选取Copula 函数描述随机变量之间相关性时需要进行参数估计,根据Copula 函数的不同,C(u1,u2,…,un|θ)的表达式也不同,其中θ为对应函数参数[5]。
2.2 R藤Copula模型
R 藤Copula 模型通过一定规则的树结构,将多维随机变量的相关性问题表示为多个二维随机变量的相关性问题。d维随机变量的R 藤Copula 模型由d-1 层树组成,记T1、T2、…、Td-1。用e表示边,第m层树的边集合为em,节点集合为Nm。当d维随机变量的R藤Copula模型结构确定后,式(4)的联合概率密度为:

1)m=1时,D(e)为空集,i和j分别为边e两端的节点。
2)m≠1 时,记第m-1 层树中相邻两边包含元素分别构成的集合为S1和S2,则D(e)=S1∩S2。记T′=S1∪S2-S1∩S2,则i,j∈T′且i≠j。
d=5时某R藤Copula模型结构如图2所示。
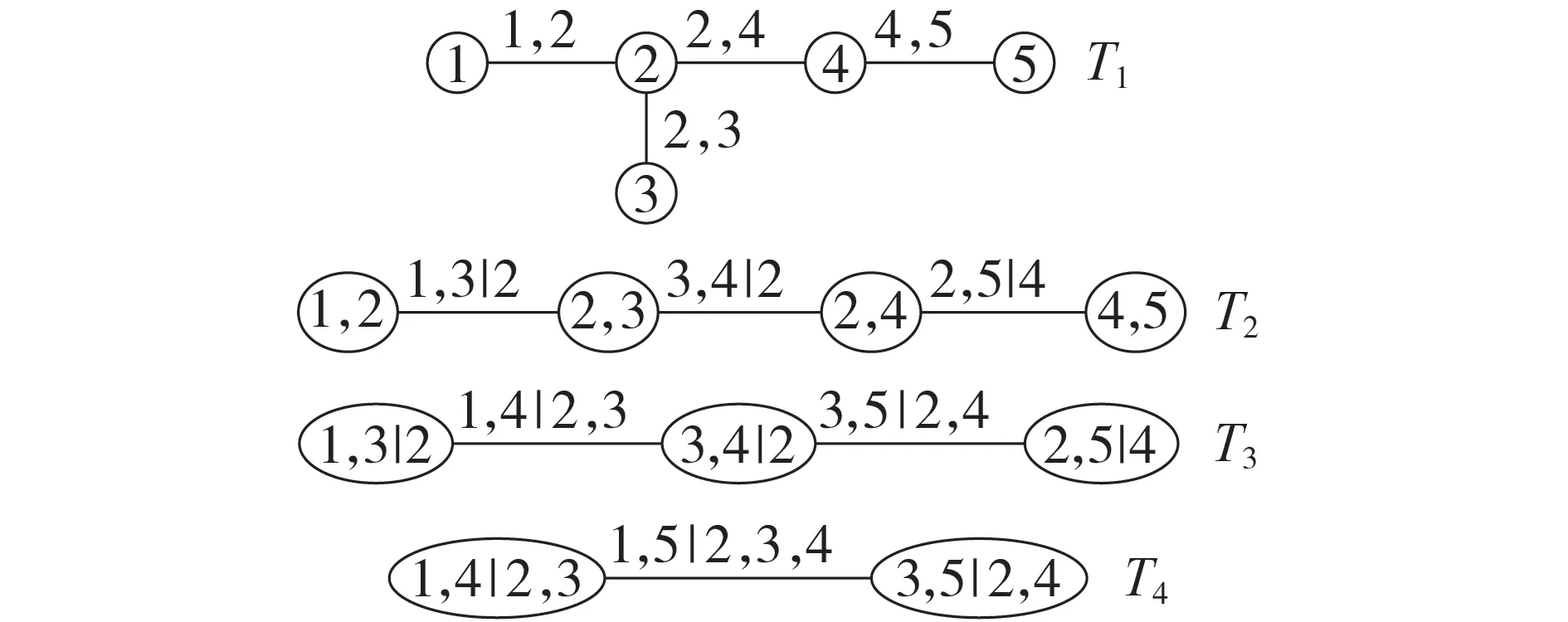
图2 某5维随机变量的R藤Copula模型结构Fig.2 Structure of Regular Vine Copula model of a five-dimensional random variable
d维R藤Copula模型对相关性的刻画通过式(6)体现,即与R 藤Copula 模型的d-1 层树及各层所选二元Copula 函数有关。R 藤Copula 模型最优的第一层树结构常通过求取不同二元Copula 函数对应的Kendall 秩相关系数并结合最大生成树法确定。最优的第一层树结构确定后,根据性质1)和2)逐层确定各层树结构及各边对应的Copula 函数,即可建立R 藤Copula 模型,从而对多维变量的相关性进行刻画,但在高维背景下,即使是非参数R 藤Copula 模型[6],也需要逐层优化求取参数,计算量巨大。
对比R 藤Copula 模型和贝叶斯网络模型可知,两者均是通过一定规则的拓扑结构描述来刻画多维变量的相关性,且R 藤Copula 模型的第一层树结构与贝叶斯网络的有向无环图相似,仅缺少对变量间因果关系的描述,此外,贝叶斯网络无需逐层优化求取参数,求解较为简单,而R藤Copula模型在高维背景下不存在难以确定最优模型结构的问题。结合R藤Copula 模型和贝叶斯网络各自的优缺点,本文基于R藤Copula模型的第一层树结构和传递熵建立初始网络B0,以刻画多维风光荷功率空间相关性。
3 R藤Copula-DBN的建立
3.1 R藤Copula最优树结构的确定
本文估算二元Copula 函数的概率密度,基于此计算Kendall秩相关系数,并将其作为最大生成树法的权重,从而确定R 藤Copula 模型最优树结构。具体求解步骤如下。
1)确定多维随机变量的边缘分布。
基于非参数核密度估计法获得风光荷功率的概率密度函数fi(xi),计算其边缘分布Fi(xi),将风光荷功率对应的随机变量xi转换为符合[0,1]均匀分布的观察变量pi,并计算其反函数F-1i(pi)。pi满足:
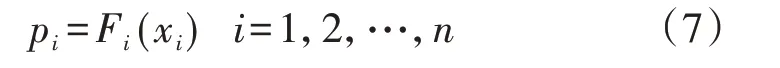
2)确定R藤Copula模型最优树结构。
采用非参数核密度估计二元Copula函数的概率密度,根据式(8)、(9)确定Kendall秩相关系数,对多维风光荷功率两两间的空间相关性强弱进行分析,并基于最大生成树法确定R藤Copula模型最优的第一层树结构。最大生成树法要求连通图中每个节点相连的边代表的权重之和最大,且对于含有N个节点的连通图,最大生成树中有且仅有N-1 条边。本文以二元Copula 函数的Kendall秩相关系数为权重,搜索满足权重之和最大的连通图结构,并将其作为R藤Copula模型最优的第一层树结构。
Copula概率密度函数积分公式为:
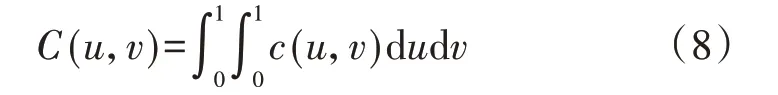
Kendall秩相关系数τ[7]为:
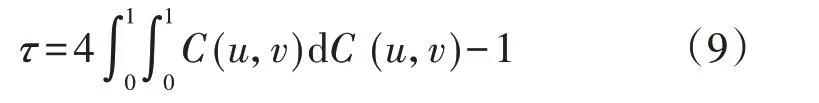
式中:C(u,v)为Copula 函数;u=F(z),v=G(y),F(z)和G(y)分别为随机变量Z和Y的分布函数。当随机变量Z和Y随时间变化时,式(9)计算的是相同时段下随机变量Z和Y的秩相关系数。
若τ=1,则表示两随机变量完全呈正相关;若τ=-1,则表示两随机变量完全呈负相关。τ越大,表示两随机变量相关性越强。
3.2 初始网络B0的建立
建立初始网络B0需要确定网络基本结构,即网络内相邻节点的因果关系。首先,将前述确定的R藤Copula 模型最优的第一层树结构作为B0的基本结构;然后,通过传递熵确定相邻变量间的因果关系。传递熵度量变量因果关系原理[17]如下:
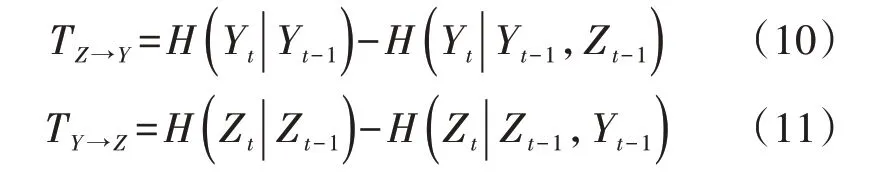

若TZ→Y>TY→Z,则称Z为因,即父节点,称Y为果,即子节点,以此确定两相邻变量间的因果关系,从而建立起完整的初始网络B0。
3.3 转移网B→的建立
转移网B→的形成服从马尔科夫过程,即随机变量当前时刻的状态仅与该随机变量的上一时刻状态相关。将初始网络B0按历史多维风光荷功率时间点序列进行延拓,并将相邻时刻单一变量的状态量彼此之间按时间先后顺序连接形成有向边,即可建立刻画多维风光荷功率时间自相关性和空间相关性的转移网B→。
3.4 DBN参数学习
由于风光荷功率均为连续型变量,在DBN 进行参数学习之前,需先对连续的服从均匀分布的观察变量pi进行等宽离散化处理,离散区间宽度取为0.01,离散区间数为100。根据建立的DBN,采用最大似然估计方法进行参数学习,得到从父节点到子节点之间的条件概率,从而建立起能够完整刻画多维风光荷功率时空相关性的R藤Copula-DBN。
3.5 多维风光荷功率概率预测
假设历史数据时段长度为T,将该时段中各时刻表示为{t1,t2,…,tT},以图3 中R 藤Copula-DBN 为例,对长度为M的未来时段风光荷功率进行概率预测,未来时段中各时刻表示为{tT+1,tT+2,…,tT+M}。具体预测步骤如下。
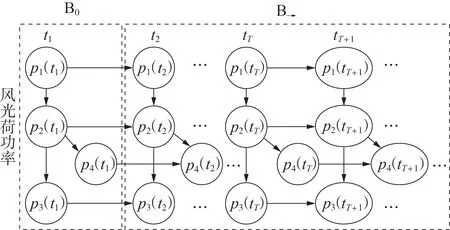
图3 R藤Copula-DBN示例Fig.3 Instance of Regular Vine Copula-DBN
1)在tT+1时刻,确定网络中仅为父节点的变量p1以及历史数据时段该变量的状态转移概率PB→(p1(ti+1)|p1(ti))(i∈[1,T-1],T≥2),通 过tT时 刻的p1(tT)计算p1(tT+1)服从的概率分布。
2)计算变量p1所有子节点所服从的条件概率分布。以子节点p2为例,按步骤1)中的方法计算变量p2在tT+1时刻所服从的概率分布P(p2(tT+1)|p2(tT)),再根据变量p2与变量p1的因果关系计算条件概率P(p2(tT+1)|p1(tT+1)),从而计算变量p2在tT+1时刻 服从的条件概率分布P(p2(tT+1)|p2(tT),p1(tT+1))。
3)按步骤2)中的方法计算变量p2所有子节点所服从的条件概率分布,得到所有变量在tT+1时刻所服从的概率分布。
4)重复以上步骤,直至计算完未来时段{tT+1,tT+2,…,tT+M}中所有时刻各变量服从的概率分布。由3.4 节离散化时的等宽区间对所有变量进行离散还原,还原的数值取对应区间的中位值。由3.1节中累积分布的反函数F-1i(pi)计算风光荷功率对应的随机变量xi。至此,完成对多维风光荷功率在未来时段的概率预测。
取各变量在未来不同时刻概率最大值所在区间的中位数作为点预测值,即可对未来时段的风光荷功率进行确定性预测。当风光荷功率维数更大时,参考本节步骤对更加复杂的R 藤Copula-DBN 进行计算。
4 算例分析
以美国南部地区4座风电场、9座光伏电场历史出力数据以及区域内3 个子地区的历史负荷数据为例进行算例分析。由于风光荷功率具有季节特性,因此在本文算例中对全年8 760 h 的风光荷功率数据按季度划分。由于样本为1 a的数据,因此冬季数据采用2020年1月、2月及12月的数据。此外,由于光伏出力具有日特性,即仅在白天有光伏出力,因此本文算例在区分季节特性的基础上进一步过滤数据,只保留1 a内每日07:00—19:00时段中的风光荷功率数据。在此基础上,采用所提方法按季度分别分析多维风光荷功率两两间的时空相关性。
采用2 个月数据对模型进行训练,然后对下一个月的风光荷功率进行预测。本文分别以3 月与4月、6 月与7 月、9 月与10 月、12 月与1 月的数据进行模型学习,预测5、8、11、2 月的风光荷功率,即月度预测。为验证所提方法在结构学习上的优越性,分别采用文献[7]中的方法、MMHC 算法以及HC 算法建立DBN 进行风光荷功率预测,以进行对比。同时,与SVR、深度置信网络和LSTM 神经网络等模型进行对比,以验证本文模型的有效性。
4.1 初始网络B0的建立
DBN 为初始网络B0在风光荷功率时间点序列上的延拓,因此初始网络B0的建立需要分析同一历史数据时段风光荷功率的空间相关性。通过非参数核密度估计法估计同一历史数据时段风光荷功率的概率密度函数和累积概率,再结合二元Copula 函数计算Kendall秩相关系数,从而对该历史数据时段风光荷功率两两之间的空间相关性进行定量分析。构建R 藤Copula 模型第一层树结构,保留风光荷功率两两相关的重要信息。以Kendall 秩相关系数给出不同季节下R藤Copula模型第一层树结构描述的风光荷功率空间相关性强弱,结果见附录A表A1。
由于相关性分析结果受所选取算例的影响,本文仅以该算例为例,对所提R 藤Copula 动态贝叶斯模型效果进行检验,以验证本文所提方法在综合考虑风光荷时空相关性的基础上,在提升计算效率和概率预测精度上的优越性。基于已求得的不同季节下R藤Copula模型的第一层拓扑结构,按3.2节中方法建立初始网络B0。刻画秋季多维风光荷功率之间空间相关性的初始网络B0见附录A图A1。
4.2 转移网B→的建立
本文建立的转移网由若干个时间片相连,时间片个数由历史风光荷功率数据的长度和待预测时刻数共同决定。在转移网B→中,连接相邻时刻时间片的有向边分别描述了风电功率、光伏功率和负荷功率在时间上的自相关性,未来时刻的风电、光伏及负荷功率除了和其他地理位置的风电、光伏、负荷功率有一定的空间相关性,还受其自身在上一时刻的状态影响。
4.3 R藤Copula-DBN模型与传统DBN模型的对比
本文所建R 藤Copula-DBN 与传统DBN 的差别在于初始网络的构建方法不同,为验证基于R 藤Copula 构建初始网络的优越性,建立以下模型进行对比:模型1,基于HC 算法的DBN;模型2,基于MMHC 算 法 的DBN;模 型3,基 于Vine-Copula 的DBN;模型4,R藤Copula-DBN。模型1—4的区别在于分别选取HC 算法、MMHC 算法、文献[7]中Vine-Copula方法以及本文所提方法进行初始网络B0的结构学习。为对比不同初始网络B0结构学习方法,假设模型1—4 的转移网络B→构建过程相同,即仅对比不同初始网络B0结构学习方法描述多维风光荷空间相关性的效果。
以秋季为例,用本文模型预测11 月30 d 内07:00—19:00 时段中风光荷功率服从的概率分布。按照3.5节中的方法,先对同一时刻下的风光荷功率按附录A 图A1 中的因果关系从父节点到子节点逐个进行预测,再对下一时刻所有地点的风光荷功率进行概率预测。地区1中11月30 d内07:00—19:00时段中共390 个预测时刻的负荷功率预测值如图4所示。
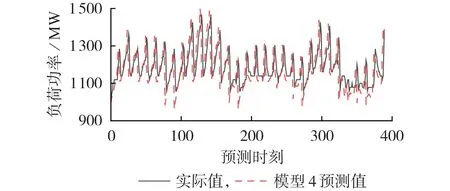
图4 秋季时负荷功率点预测结果Fig.4 Point prediction results of load power in autumn
90%置信度下,风电场1 在8 月1 日至8 月23 日07:00—19:00 时段中共299 个预测时刻的出力概率区间结果见附录A 图A2。考虑到算例数据仅保留每天07:00—19:00 时段的数据,本文模型概率预测的结果与一般的日前或日内多点预测有所不同。若要进行连续24 h 的小时级预测,则需进一步考虑夜间光伏出力为0 的情况,此时光伏与风电、负荷功率的空间相关性极弱,可忽略不计,因此应对每天20:00至次日06:00多维风荷之间的空间相关性进行分析,通过建立本文模型进行概率预测,光伏则单独考虑,此时建立的初始网络模型中,代表光伏的节点与其他节点没有因果关系,概率预测仅考虑光伏功率的时间自相关性。
本文模型的预测结果与算例数据的采样时间间隔有关,当算例数据为每小时的数据时,可实现小时级的预测。当算例数据为每半小时或每15 min的数据时,本文模型可更准确地描述同一历史数据时段下风光荷功率间的空间相关性,且对风光荷功率时间自相关性的刻画更加精细,并实现日内半小时或间隔15 min的预测。
对不同模型的概率预测效果进行评估,评估指标采用确定性预测评估指标和可靠性评估指标[1]。由于风电和光伏功率存在零值,平均绝对百分比误差MAPE(Mean Absolute Percentage Error)将失去意义,因此确定性预测评估指标通过比较点预测值与真实值之间偏差的均方根误差δRMSE和反映预测值误差实际情况的平均绝对误差δMAE来评估模型精度,详细计算公式见附录B 式(B1)、(B2)。可靠性评估指标通过比较风光荷功率实际落在概率预测区间的频率与事先给定的置信概率的差异大小来评估模型精度,即预测区间的覆盖概率指标,详细计算公式见附录B式(B3)。
表1 和表2 分别给出了不同季节时用不同模型进行风光荷功率概率预测的δRMSE和δMAE。由表可以看出:模型1 和模型2 在不同季节的预测误差相近,这表明MMHC 算法对HC 算法的改进有限;相较于模型1 和模型2,模型3 的预测精度有所提升,秋季时的提升效果最为明显,这验证了通过Vine-Copula方法学习贝叶斯网络结构的有效性;与模型3 相比,模型4的精度进一步提升,不同季节时的δRMSE和δMAE均小于模型3,验证了本文所提模型的优越性,表明了全面考虑多维风光荷空间相关性对概率预测精度提升的作用。
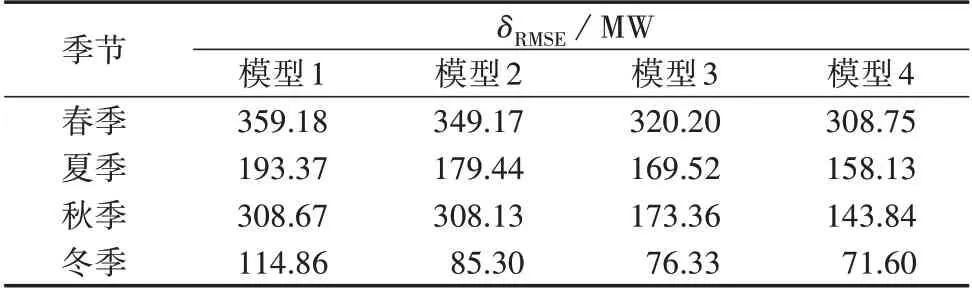
表1 均方根误差对比Table 1 Comparison of root-mean-square error
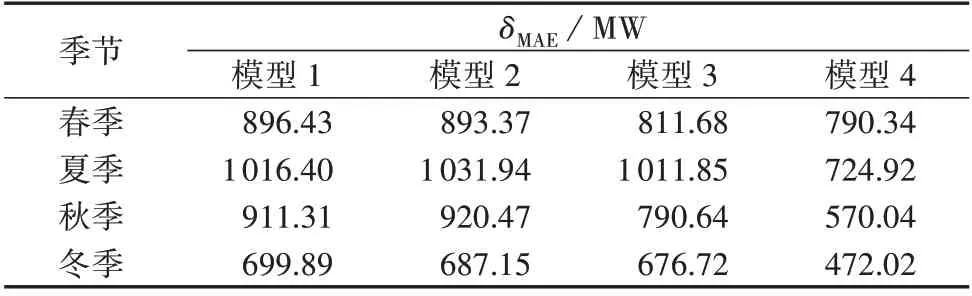
表2 平均绝对误差对比Table 2 Comparison of mean absolute error
表3给出了90%的置信度下不同季节时用不同模型进行风光荷功率预测的预测区间覆盖概率指标Rcover。由表可以看出,与其他模型相比,模型4 的预测区间覆盖概率指标最大,验证了基于R 藤Copula学习初始网络B0结构的有效性和优越性,虽然该模型最终的预测区间覆盖概率指标没有达到置信度90%,但已较为接近。此外,和常用的K2算法相比,本文所提方法无需依靠主观经验预设节点顺序,可避免主观因素产生的影响。与MCMC、HC 和MMHC等算法相比,本文所提方法可确定唯一最优结构,且该结构具有稀疏性,缩小了结构搜索的空间,减少了计算量。
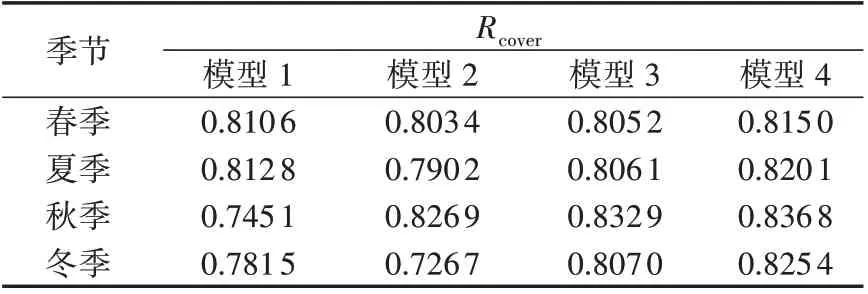
表3 预测区间覆盖概率指标对比Table 3 Comparison of prediction interval coverage probability index
4.4 R 藤Copula-DBN 模型与SVR、神经网络等模型的对比
为验证本文所提模型的有效性,建立以下对比模型:模型5,SVR[9];模型6,LSTM 神经网络[10];模型7,深度置信网络[11]。为提高不同模型概率预测结果对比的可靠性,对预测精度易受参数影响的模型5—7 分别进行参数调优。其中,模型5 通过分散搜索算法[18]进行参数的优化,模型6和模型7均采用Adam 优化器[19]进行模型参数的优化。模型5 表示的回归模型无法同时对多个风光荷功率进行预测,因此该模型需要对多维风光荷功率进行逐个预测。模型6 和模型7 则通过神经网络对变量之间的非线性相关特征进行刻画,对同一时刻下所有地点风光荷功率同时进行预测,再预测下一时刻风光荷功率的概率分布。
附录A图A3给出了11月模型4—7部分时刻负荷功率预测值与实际值的对比。结果表明,模型5—7 的点预测结果均存在较大的偏离实际值的值,而模型4的预测结果与实际值较为接近,表现更好。
模型精度评估指标与4.3 节相同,结果见附录A表A2—A4。结果表明:秋季时模型5 预测总误差δRMSE和δMAE相对较大,模型5预测结果中偏离实际值的值较多,导致模型整体精度较低;模型6 的预测误差与模型5相近,这表明模型6的预测结果中同样存在较多偏离实际值较大的值;模型7 的预测精度较模型5 和模型6 有所提高,因此模型7 有较高的预测区间覆盖概率指标;模型4和模型7的预测精度较为相近,且预测区间覆盖概率指标相近,验证了本文所提模型的有效性。
考虑到SVR、LSTM 神经网络以及深度置信网络在刻画时间序列自相关性上的优缺点,以8月地区1负荷点预测结果为例,对比不同模型在刻画时间序列自相关性上的效果,如图5 所示。由于本文模型和模型1—3均为动态贝叶斯模型,所构造的转移网相同,则本文模型和模型1—3在刻画时间序列自相关性上的效果相同,因此无需再进行比较。由图5可以看出,本文模型刻画的时间自相关性与实际值更加接近,这表明对时间序列进行相关性建模和预测时,相较于SVR、LSTM 神经网络以及深度置信网络,本文模型表现效果更好。
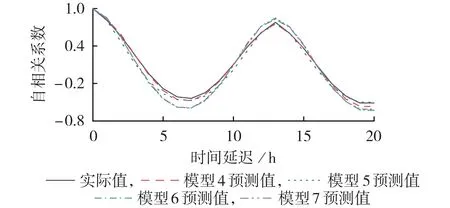
图5 不同模型刻画时间自相关性效果对比Fig.5 Comparison of effect in describing time autocorrelation among different models
不同模型的计算时间对比见附录A 表A5。结果表明:模型5 的计算时间最短,但由于该模型精度较低,因此总体表现上略差于本文模型;与模型6 相比,本文模型在提升计算精度的同时,极大地提高了计算效率,表现效果更优;本文模型和模型7 的计算效率较为接近,验证了本文模型的有效性。
5 结论
为更准确、便捷地描述多维风光荷间的空间相关性,结合R藤Copula和贝叶斯网络各自的优点,本文建立R 藤Copula 贝叶斯网络,并将其扩展到时间轨迹上建立可描述时空相关性的R 藤Copula-DBN,并将其应用于计及时空相关性的多维风光荷功率概率预测。主要结论如下。
1)本文所提初始网络B0的结构学习方法具有一定的稀疏性,可缩小结构搜索的空间以及减少计算量。通过与基于HC 算法、MMHC 算法及文献[7]中方法建立的DBN 模型精度的对比,验证了本文所提初始网络B0结构学习方法的有效性。
2)本文模型在概率预测时比SVR 和LSTM 神经网络的效果更好,且模型精度与深度置信网络相近,这表明了本文模型的有效性。此外,本文模型在刻画自相关性上的效果优于SVR、LSTM 神经网络和深度置信网络,计算时间上与深度置信网络相近,验证了本文所提方法的有效性。
3)基于R 藤Copula-DBN 刻画时空相关性的风光荷功率概率预测,综合考虑了风光荷之间的时空相关性,可为电力系统安全稳定运行提供参考。
本文主要考虑风光荷功率时间相关性中的自相关性以及风光荷功率空间相关性在时间域上的一致,这对风光荷复杂相关性的挖掘并不全面,未来可对考虑风光荷时变空间相关性及时间自相关性的建模进行研究。
附录见本刊网络版(http://www.epae.cn)。
