不同支撑形式的型钢混凝土阀厅抗震性能分析

程 亮，高 湛，吴必华，杨 超

（1．中南电力设计院有限公司，湖北 武汉 430071；2．武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070）

0 引言

由阀厅建造材料和结构受力的不同，主要分为全混凝土结构、全钢结构、钢－钢筋混凝土混合结构三种结构形式。其中全混凝土结构在水平地震作用下表现不佳，因此高度较大的阀厅一般不予采用。全钢结构阀厅和混合结构阀厅由于四面或三面为钢柱，防火性能较差，特别是换流站阀厅存在特高压电网，极易发生火灾，还有造价高，维护困难等问题。使用型钢混凝土结构替代钢－钢筋混凝土混合结构阀厅中的钢结构框架，可较好的解决上述问题。同传统的钢结构相比，型钢混凝土结构有更大的刚度和强度，更好的局部和整体稳定性，耐腐蚀和防火性能好，节约钢材。同时，与全钢筋混凝土结构相比，这种结构承载力和刚度大，具有更好的变形能力和延性，抗震性能优越［1－3］。

阀厅结构具有跨度大、结构体型不规则的特性，在地震作用和自身设备等荷载作用下，整体结构受力十分复杂，且两种不同形式材料的特征对整体结构也有一定的影响。此外，在不同的使用环境下，不同形式的支撑对结构的动力特性也有影响。为此，为了更好的研究带支撑的型钢混凝土阀厅结构在地震作用下的内力和变形特征，采用动力时程分析对两种典型的支撑阀厅的整体结构的抗震性能进行分析，为进一步推进该结构的使用打下良好基础。

1 两种支撑形式的整体模型的建立

依据实际工程，选择某典型的混凝土阀厅，改为型钢混凝土阀厅，其中结构的尺寸为86．2 m×56 m，山墙高度为33 m，屋面采用钢屋架与型钢混凝土柱连接，二者的连接形式为铰接［4］，屋架下弦距地面高度为26．05 m，上弦距地面高度为30．05 m。为较好的分析型钢混凝土阀厅中设置不同类型支撑的影响，分别选择X 形和人字形两种形式的支撑结构［5］，前者刚度较大可以抵抗较大水平荷载，后者则方便仪器设备和车辆通行，均有各自的优势，其在阀厅结构的纵轴中的布置如图1，图2 所示。

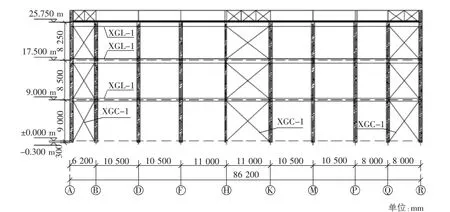
图1 阀厅结构纵轴X 形支撑布置图

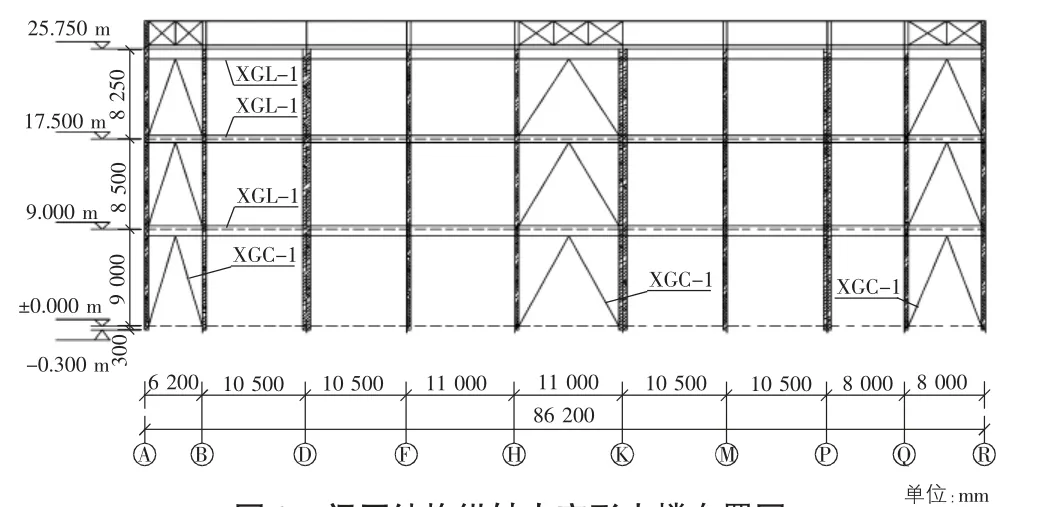
图2 阀厅结构纵轴人字形支撑布置图

采用SAP2000 建立了型钢混凝土阀厅结构的整体有限元模型。建模过程中采用框架单元模拟实际结构中的柱、梁和斜撑，对于非承重构件，将其自重转换为相应的集中力添加到结构上，X 形和人字形两种形式的支撑结构的有限元模型可见图3，图4。

图3 阀厅结构纵轴X 形支撑布置图

图4 阀厅结构纵轴人字形支撑布置图

2 模态分析

模态是结构的固有振动特性的研究，包含固有频率、阻尼比和振型，是进行动力特性和抗震分析的前提和准备。基于软件特有的“质量源”特征，并考虑规范中对重力荷载代表值的定义，设定具体的“质量源”。同时，考虑到结构体系高阶振型因衰减较快，导致对整体动力特性影响较小，为方便研究，仅考虑其前三阶振型进行分析，根据计算分析，得出其振型信息如表1 所示。

表1 模型整体振型方向及周期

由分析可知：两种支撑形式的型钢混凝土阀厅结构的前三阶振型分别为朝Y向（横向） 平动、朝X向（纵向）平动、扭转，这说明两种形式的支撑作用下，结构的整体刚度分布均较为均匀，结构布置合理，也符合初步设计中整体结构纵向刚度要比横向刚度大这一特征。型钢混凝土阀厅结构自振周期随着振型阶次的增加而逐渐减小，振型刚度随着振型阶次的增加而逐渐增加。对比两种形式的模态计算结果，X 形支撑的周期值均小于人字形的，与该形式结构刚度大于人字形相符。综合模态分析结果，该模型设置合理，可用于后续的动力时程分析。

3 多遇地震下的时程分析

时程分析法是对结构动力方程直接进行逐步积分求解的动力分析方法，可以得到质点随时间变化的动力响应，并进而求出构件内力的时程变化关系，是现阶段对结构抗震性能最为直接的分析方法。现采用SAP2000 软件对结构进行时程分析，选取El-centro 地震波、Taft 地震波进行计算，并且依据规范［6］要求选取了一条人工合成地震波（以下简称人工波） ，各波型加速度时程曲线分别如图5 ～图7 所示。

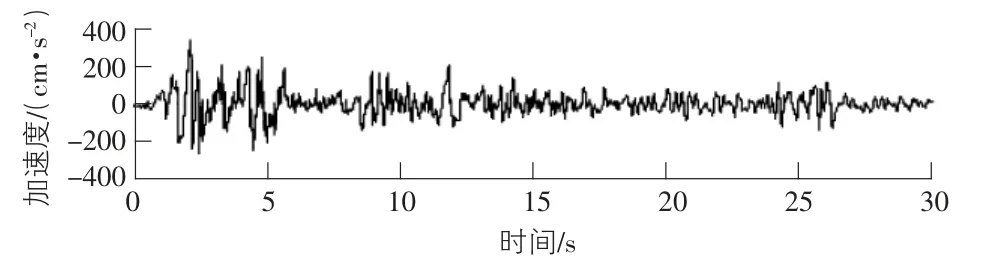
图5 El-centro 波加速度时程曲线

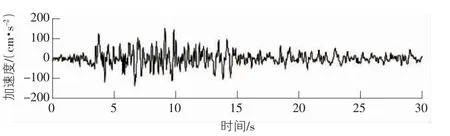
图6 Taft 波加速度时程曲线

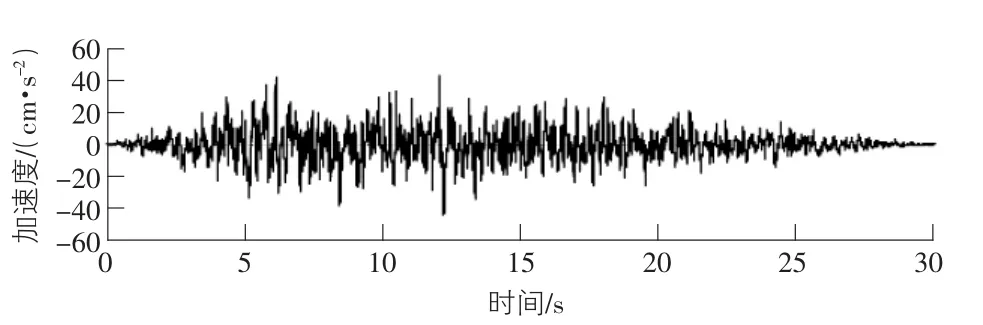
图7 人工波加速度时程曲线

将三条地震波的加速度峰值按照抗震设防烈度7 度，设计地震基本加速度0． 15g 的多遇地震调整为0．55 m/s2，采用单方向（X向） 输入地震波，将各模型柱底剪力幅值进行比较，如表2 所示。

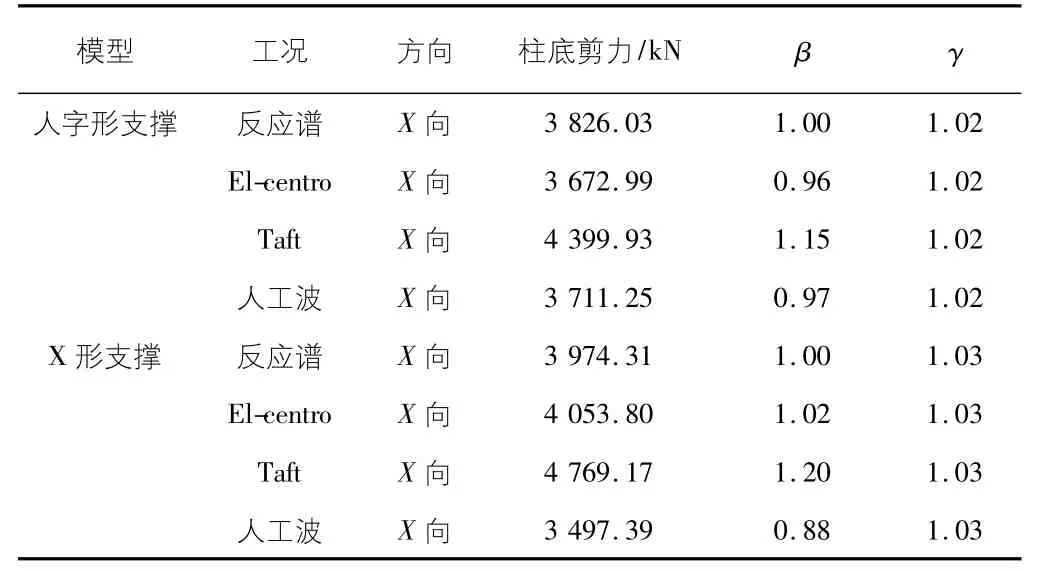
表2 时程分析法和反应谱法结构柱底剪力幅值比较

表2 中β表示时程曲线计算所得的结构底部剪力与振型分解反应谱法计算结果的比值，γ表示多条时程曲线计算所得结构底部剪力的平均值与振型分解反应谱法计算结果的比值。其中反应谱是基于GB 50010—2010建筑抗震设计规范的设计加速度反应谱，按抗震设防烈度7 度，设计地震基本加速度0．15g，场地类别Ⅲ类，设计地震分组为第二组计算的柱底剪力值。由表2 可知，选取El-centro 波、Taft 波和人工波时程曲线是符合规范［6］要求的。

通过动力时程分析，获得了两种不同结构形式在7 度0．15g 的多遇地震作用下柱底剪力（见表2） ，其剪力满足结构的抗剪设计要求。两种形式的结构的最大层间位移分别为0．19 m 和0．17 m，而结构的总高为26．05 m，因而层间位移角分别为1/1 372 和1/1 532，均远小于设计位移角要求，从而说明配有此两种形式支撑的型钢混凝土阀厅结构在地震作用下变形性能良好，能满足一般阀厅的抗震要求。利用反应谱法计算得到的人字形支撑的基底剪力值与人工波得出的相近，而X 形支撑的反应谱结果则与El-centro 波作用下接近，但整体差值符合分析要求。两种支撑的抗侧对比发现，X 形支撑的抗侧能力更强，在满足工艺和建筑要求的前提下，采用X 形支撑能提供更好的抗震性能。

4 结论

本文选取某实际的混凝土阀厅结构为原型，在将其改进为型钢混凝土阀厅结构后，利用有限元分析软件SAP2000，建立了两种典型形式（X 形和人字形） 支撑的型钢混凝土阀厅结构整体有限元模型，对其进行动力时程分析，主要结论如下：

1） 由模态分析可以得出结构的前三阶振型和自振周期，其中前两阶振型为平动，第三阶为扭转，结构体系的布置满足一般设计要求。同时结构刚度和周期也符合预期分析，表明整体结构模型建立合理，选择的地震波满足规范的选波要求，可以利用此整体模型和地震波进行动力时程分析。

2） 选用El-centro 波、Taft 波和人工波对阀厅结构进行了动力时程分析，获取其柱底剪力和位移变形，两种地震波作用下，两种不同形式支撑的型钢混凝土阀厅结构的内力和变形均满足设计要求，显示出带支撑的型钢混凝土结构良好的抗震性能，可以作为主要结构形式用于阀厅的使用。

3） 不同地震波作用下两种形式的支撑计算得出的剪力值，与反应谱计算得出的有所差别，但均满足分析要求，也均显示了良好的抗震性能，显示出两种支撑对抗侧和抗震的作用。X 形支撑的抗侧及抗震能力更强，在满足工艺要求的前提下，采用X 形支撑能提供更为良好的抗震能力。