疾病治疗质量综合评价的维度融合方法研究*

哈尔滨医科大学卫生统计学教研室(150081) 栗景坤 包晓蔷 李 习 王 超 刘梦洋 田 园 刘美娜

治疗质量是指在现有医疗环境和资源的情况下，不增加病人经济负担，利用循证医学验证的有效治疗方法制定的最合理诊疗式，其本身是一个不可直接测量的变量[1]。进行医院的治疗质量综合评价，需要考虑疾病诊疗的全部过程，如检查、手术、功能评价和结局等[2]；其中涉及多个治疗维度及相应评价指标[3]，为获得客观、全面且具有代表性的治疗质量，需要将多个维度的治疗质量进行合理融合获得综合评价结果，确定维度间权重成为获得综合治疗质量的关键。

多目标决策方法如层次分析法中的权重判断矩阵也仅以0、1作为指标的隶属度，在处理实际问题时显得过于绝对，缺乏科学性[4]。模糊综合评价是对受多种因素影响的事物做出全面评价的一种有效的多因素决策方法[5]，但模糊比较算法在模糊数接近或者模糊区间嵌套时常无法获得稳定权重[6-9]。鉴于此，本文提出新的模糊算法计算治疗质量各维度的权重，引入信息熵来降低变异较大的模糊数对最终权重稳定性的影响。

维度融合方法的建立

1.计算治疗质量各维度得分

假设医院某疾病的治疗质量可分为m个维度(θ1,θ2,…，θm)，每个维度包含k个指标。医院所有患者应该使用的指标个数作为分母，实际使用的指标个数作为分子，则第i个治疗质量维度指标分子集合为(vi1,vi2,…vik)，分母集合为(ni1,ni2,…nik)，i=1,2,…,m，采用分母权重法[10-11]计算医院第i个维度治疗质量综合得分:

2.确定初始权重

首先，获得维度间模糊判断矩阵：邀请p名专家对维度i和维度j进行模糊比较，并将比较的三角模糊数mpij=(lPij,mPij,uPij)用于生成矩阵，其中lPij为最悲观估计，mPij为最可能估计，uPij为最乐观估计。

f(x)为隶属函数为：

隶属函数表示x对模糊数M的隶属程度，为方便后文讨论，本方法将区间[l,u]定义为模糊区间，[l,m]定义为悲观区间，[m,u]定义为乐观区间。

其次，引入信息熵。传统的模糊矩阵一般由多名专家给出模糊判断后直接取均值，本质上并没有去除主观因素的影响；在不同专家对同一次模糊比较的结果差异较大时，对确定最终权重会有影响，如模糊区间过宽、无法得到稳定权重等。因此，本方法将信息熵引入整合多名专家判断结果的过程中，消除专家意见差异较大时的主观影响。

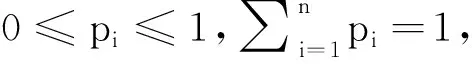
当专家对同一次维度间比较得出的模糊区间差异较大时，该次比较的信息熵较小；基于多名专家比较结果的信息熵进行模糊数正向加权，获得熵优化的模糊判断矩阵。

rpij=lpij+mpij+upji

其中，

最后，计算不同维度初始权重模糊数：

i=1,2,…,m

3.计算综合治疗质量

利用治疗质量初始权重模糊数去模糊化获得最终权重，结合治疗质量各维度得分计算融合后的医院综合治疗质量。在去模糊化时，本文综合考虑两个模糊数共同取值的公共区间及模糊数单独取值的自由区间，对最可能估计的作用加以限制，当重叠区间不同时包括两个模糊数的最可能估计时，有m2大于m1的程度为百分之百，定义V(m2>m1)为模糊数m2大于m1的程度，即V(m2>m1) =1，m2≥m1+u1-l2，同时为了方便计算，更加精确的划分分段公式的区间。结合概率统计的知识，具体如下

a:m2≥m1+u1-l2

b:m1+u1-l2≥m2≥m1,l1≤l2≤u1≤u2,

c:m1≥m2,l2≤l1≤u2≤u1

d:l1≤l2≤u2≤u1

e:l2≤l1≤u1≤u2

f:u2≤l1

按照上述算法进行治疗质量初始权重模糊数的去模糊化，采取累加归一化的方式计算维度最终权重，得到w=(w1,w2,…，wm)，为各维度标准化权重向量，进行各维度治疗质量得分的融合，获得综合治疗质量θ。

i=1,2,…m

模拟研究1

治疗质量维度融合时，需要邀请专家进行维度间重要程度的模糊比较，常出现专家意见不一致的治疗质量维度模糊数波动。模拟研究1目的是在专家对治疗质量维度进行比较，意见不统一时，本文建立的方法能否获得稳定的治疗质量维度间权重，计算医院各维度治疗质量及维度融合的综合治疗质量得分并排名。

基于治疗质量评价背景和医疗领域实际情况，设定治疗质量的维度3个，每个维度包含4个评价指标，3名专家进行维度间比较获得模糊矩阵。

1.模拟条件设置

设置维度1与维度3的比较结果存有争议，不同专家的判断差异较大；维度2与维度1、维度2与维度3的比较结果一致，不同专家的判断差异较小。

模拟生成100家医院，每家医院每个维度评价指标的分母(应该使用此指标的患者数)设置为10000，分子(实际使用此指标的患者数)从U(4000，8000)，U(6000，9000)，U(7000，10000)，产生并取整数生成模糊矩阵，见表1。

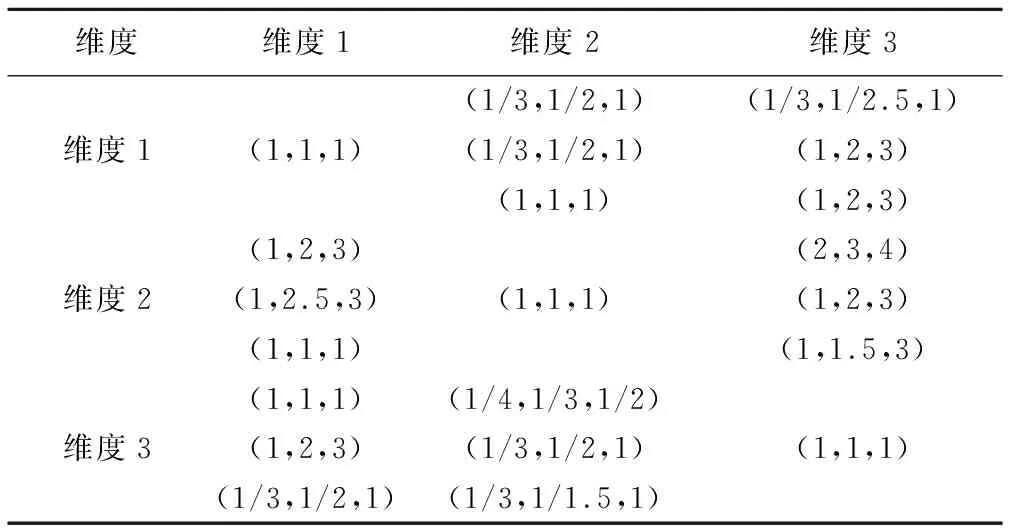
表1 治疗质量维度两两比较判断矩阵

2.确定维度权重

利用本方法，获得各维度的初始权重模糊数集，见表2；获得3个治疗质量维度的最终权重结果，见表3。本方法兼顾了维度1和维度3的争议，及专家主观意见不同所引起的模糊判断波动，降低了有争议的治疗质量维度所占的权重。

表2 治疗质量初始权重模糊数

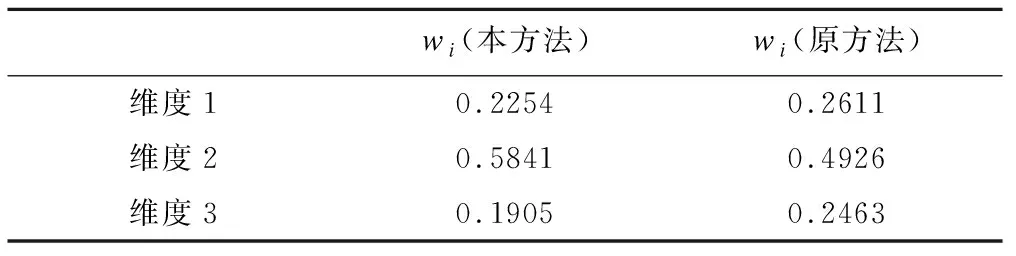
表3 治疗质量维度最终权重

3.维度融合治疗质量及医院排名

根据治疗质量评价指标分子分母和治疗质量维度权重，获得医院各维度治疗质量得分及维度融合后的综合治疗质量得分，见表4；利用维度融合的综合治疗质量和单维度治疗质量得分，进行模拟产生100家医院治疗质量排名，取前15家医院，见表5。

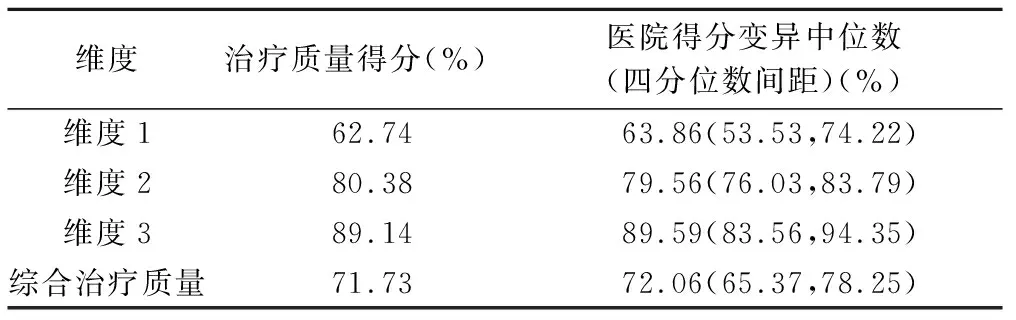
表4 治疗质量维度及综合得分

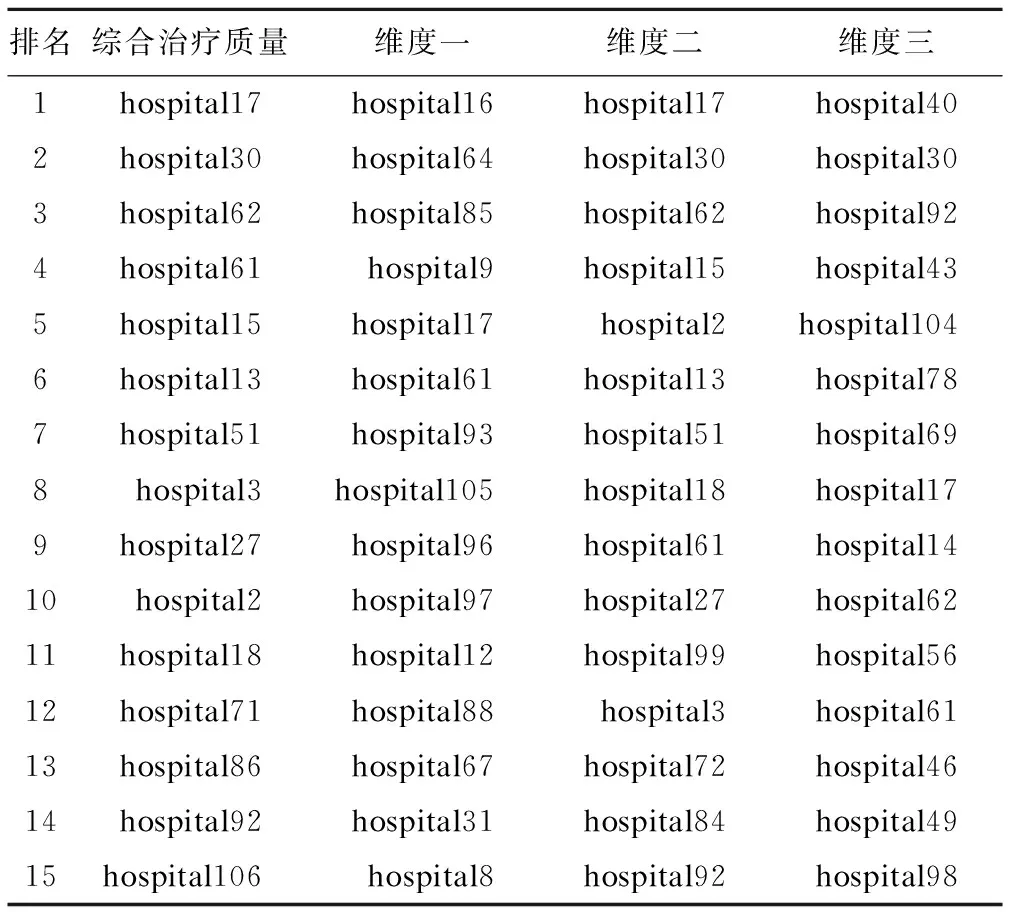
表5 不同评价方法排名前15名医院

综合得分排名前15名医院中，分别有2家、11家、5家医院在治疗质量维度一、二、三排名中进入前15名；hospital17、hospital61两家医院在4次排名中均进入前15名。

模拟研究2

治疗质量综合评价指标来自多个维度，当专家给出维度间重要程度比较的差异较大时，会导致权重模糊数区间变大，原方法会出现维度权重为0或无法得到稳定权重。模拟研究2目的是在权重模糊数区间大时，检验本方法能否兼顾治疗质量维度差异获得符合模拟条件设置的稳定权重。

1.模拟条件设置

设置维度3的重要程度较高，其次为维度2，维度1重要程度最低；维度数、指标数、专家数设置同模拟研究1。生成模糊矩阵，见表6。

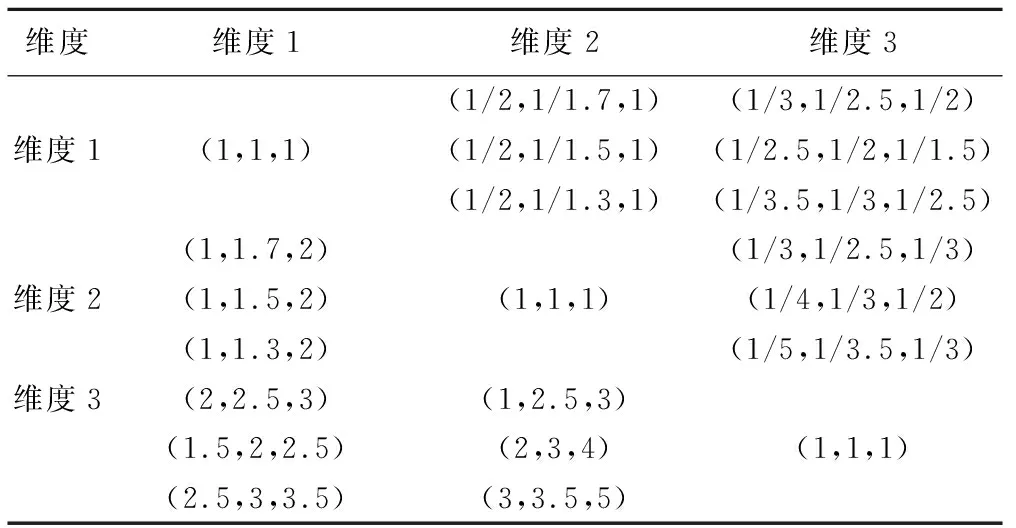
表6 治疗质量维度两两比较判断矩阵

2.确定维度权重及权重比较

利用本方法，获得各维度的初始权重模糊数集，见表7；分别计算本方法及原方法的治疗质量各维度权重，见表8。

表7 治疗质量初始权重模糊数

表8的结果显示，原方法结果中出现权重为0，且非0权重不稳定的情况，无法获得维度融合的最终的治疗质量。本文建立的方法得到的结果与模拟实验设置一致，可以获得更稳定的治疗质量维度间权重。

*：表中数值为与单元格所在列维度相比，行维度的重要程度。

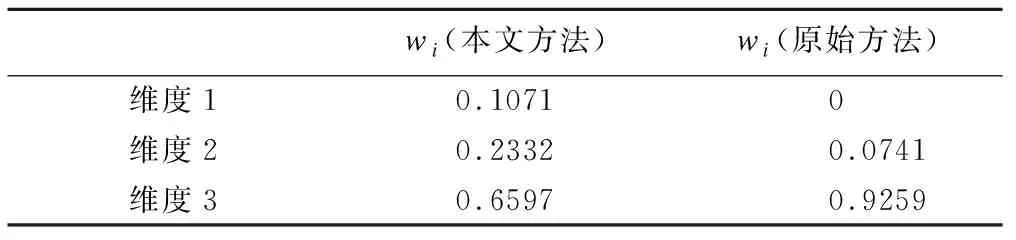
表8 治疗质量最终权重

讨 论

医院的治疗质量评价涉及到多个维度多个指标，仅利用单指标或单维度进行评价难以反映疾病治疗的整个过程，并且不同指标或维度的评价结果可能相悖[2]。合理的治疗质量评价涵盖疾病治疗过程的各个维度，治疗质量维度融合是进行综合评价的前提和基础，目前尚无多个治疗质量维度融合方法。

治疗质量维度融合关键是确定合理的维度权重，在疾病治疗过程中，每个维度在综合评价中的地位和重要性各不相同。为获得全面客观的评价结果，本文基于模糊数学建立了治疗质量维度融合方法，利用熵优化的模糊矩阵降低治疗质量维度模糊数的变异，达到维度间权重更符合治疗质量评价实际。相比于Chang Da-Yong提出的传统模糊数比较方法[12]，本方法的优点是数据变异较大时，可以获得稳定的维度间权重；设m1=(l1,m1,u1)，m2=(l2,m2,u2)，定义V(m2>m1)为模糊数m2大于m1的程度。传统方法在去模糊化过程中比较两个三角模糊数公式如下：

该方法中最可能估计所起的作用较大，且主要通过两个模糊数的重叠区间与较小模糊数的乐观区间和较大模糊数的悲观区间进行比较，计算模糊数m2大于m1的程度[13-15]，但在比较治疗质量维度时存在以下问题。

第一，两个治疗质量维度模糊数最可能估计接近时，计算结果可能有误：在图1里，模糊数较为接近，按照公式则为V(m2>m1) =1，也就是说模糊数m2所代表的治疗质量维度2的重要程度大于m1代表的维度1的程度为百分之百，显然与实际不符。

第二，当两个治疗质量维度模糊区间嵌套时，计算结果可能有误。在图2里，按照原公式V(m2>m1)应为重叠区间[l1,u2]和m2的乐观区间与m1悲观区间的比值，但原公式计算的重叠区间已经不是m2，m1共同取值的公共区间，其中区间[u1,u2]为模糊数m2的自由取值空间，将此区间直接并入重叠区间计算不合理。

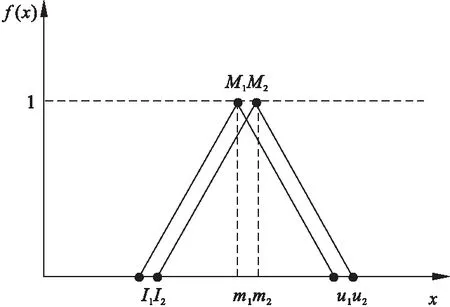
图1 m2和m1较为接近

图2 m1位于m2之内

传统方法公式的分段区间设置太过简略，计算一些区间偏态较大或两个模糊数区间互相嵌套分布时，常出现某次或多次治疗质量维度比较的模糊数为0或与实际不符的情形，不适用于计算治疗质量维度的权重。

本文建立的方法很好的解决了原方法计算不合理之处，优化了在维度模糊数特殊取值时比较结果的稳定性，更加精确的划分了公式适用区间，如：当M1=M2=(2，3，4) 时，原公式V(m2>m1)=1，本文V(m2>m1)=0.5，与实际相符；当M1=(2，2.9，4)，M2=(2.1，3，4.2)时(图1)，原公式V(m2>m1)=1，本文V(m2>m1)=0.535，与实际相符。

本文建立的治疗质量维度融合评价方法，将定性与定量结合，主观估计客观化，从治疗质量整体的角度综合各种因素，提高治疗质量评价的准确性。不足之处是仅给出治疗质量的计算结果，需要后续结合实际数据计算综合治疗质量并进行影响因素分析；由于专家数量设定有限，隶属函数的选择有待进一步优化。