未亡时间偏倚的常用处理方法及进展*

程 义 李冬冬 陈 峰 郭 威 吴 骋△

1.海军军医大学卫生勤务学系军队卫生统计学教研室(200433) 2.解放军94969部队保障部卫生队

未亡时间偏倚(immortal time bias)又称为保证时间偏倚(guarantee time bias)，是一种特殊的选择性偏倚[1]，广泛地存在于观察性研究和药物临床试验中。Gail[2]分析心脏移植的研究时，首次提出了未亡时间偏倚，认为移植组生存时间的延长，部分归因于未亡时间偏倚的存在。

在进行生存分析时，如果暴露/处理发生在随访期间，在研究开始时，所有的受试者都归为非暴露/对照组。随着随访的进行，部分患者或早或晚地接受暴露/处理，进入暴露/处理组。从进入研究队列(如移植注册)到接受暴露/处理(如接受心脏移植)的随访时间称为“未亡时间”(immortal time)。在“未亡时间”内，暴露/处理组患者的生存时间要足够长，直到接受暴露/处理；而非暴露/对照组则没有这种生存时间的要求。

在生存分析中，由于不恰当的分组方法、未能正确处理“未亡时间”，或者没有采用正确的统计学方法，都可能产生偏倚，使得分析结果夸大了暴露/处理效果。

Michele Iudici[3]等分析了风湿病领域，近5年发表在顶尖杂志上(如新英格兰医学杂志、柳叶刀、美国医学会杂志等)的78项观察性研究，其中的8项研究(10%)存在未亡时间偏倚，这种偏倚的存在，产生了有利于暴露/处理组的结果。在一项评估二甲双胍能否提高胰腺癌患者生存率的研究中[4]，由于未亡时间偏倚的存在，使得二甲双胍对胰腺癌的保护作用降低了18%。在药物流行病学研究中[5]，未亡时间偏倚也广泛存在，甚至难以识别，因此识别并控制这种偏倚，在实践中至关重要。

本文综述了处理未亡时间偏倚常用的统计学方法，包括界标分析(landmark method)、时依性Cox模型(time-varying Cox model)以及逆概率加权(inverse probability weighting，IPW)，介绍了每种方法的适用条件和优缺点，以及其最新进展和案例应用，并进行了实例分析，以期为相关领域的研究者提供参考。

常用的统计方法及比较

1.界标分析

(1)界标分析简介

界标分析是目前处理生存分析中未亡时间偏倚的主要方法之一。该方法旨在无偏地估计暴露/处理组患者和非暴露/对照组患者在界标时间的生存概率。Anderson[6]等在肿瘤学中进行应答组与非应答组的生存分析时，提出了界标分析。Charity J[7]等简要介绍了界标分析。

在界标分析中，首先选取一个固定的时间作为界标时间，以此为研究起始时间，仅保留界标时间点仍然存活且可随访的患者。根据患者在界标时间前是否接受暴露/处理进行分组。然后使用生存分析的基本方法比较两组的生存情况，如Kaplan-Meier法、log-rank检验、Cox比例风险模型等。在解释结果时需要注意，界标分析得到的结果仅适用于在界标时间时仍存在风险的患者[1，7]。常用统计软件均可实现界标分析，如R软件、SAS、SPSS、stata等。

(2)界标分析的优势和局限性

界标分析具有操作简便、描述直观以及清晰的图形化呈现方式[8]等优点，用于控制暴露/处理的时依性属性导致的偏倚，如未亡时间偏倚、领先时间偏倚[9-10]等。基于界标分析，一些更复杂的模型可用于患者生存概率的动态预测，如界标分析超级模型(landmark supermodels)[11-12]、界标治愈率模型(landmark cure rate model)[13]。

但是界标分析存在一定的局限性。首先，界标时间选取具有主观性。选取不同的界标时间，得到的分析结果也不尽相同，某个界标时间的结论难以在其他界标时间推广。因此，研究者首先需要确定，界标分析是否能够为所研究的问题提供有意义的估计，并根据疾病进程，选取有临床意义的时间作为界标时间，并且有必要选取多个界标时间进行敏感性分析，以评价结果的稳健性。

其次，统计效能和精确性下降。界标分析排除了界标时间之前的结局事件和删失数据，降低了统计效能和精确性。因此，在选取界标时间时需要权衡：选取过早的界标时间，会忽略界标时间之后发生的暴露/处理，无法进行有效的生存率的比较；选取过晚的界标时间，则会排除更多的患者，从而降低了统计效能。

此外，界标分析是基于观察性研究的，缺少了随机化属性，当结果显示组间差别有统计学意义时，干预与结局之间只能解释为“相关关系”，而非“因果关系”。

2.时依性Cox模型

(1)时依性Cox模型简介

Cox比例风险模型(Cox proportional-hazards model)是生存分析中最常用的回归分析方法，常用于探究多个协变量对患者生存时间的影响。当暴露/处理具有时依性属性时，可以纳入一个(或多个)时依性的协变量(time-dependent covariates)，采用时依性Cox模型加以控制。

时依性Cox模型本质上是增加了一个(或多个)时依性的协变量，这个变量的取值可以随时间改变，也就是说允许病人的分组在随访过程中改变。这样，暴露/处理组患者的生存时间就分为两部分：干预前和干预后。虽然分析中存在时依性的变量，但是分组后的区间里的协变量的值是不变的。通过构建风险函数，得到对风险比(hazard ratio)的估计，来定量地表示时依性协变量对结局的影响。Jiannong Liu[14]等比较了四种处理未亡时间偏倚的方法，认为“时依性Cox模型适用于分析时依性暴露/处理”。

时依性Cox模型可以通过多种统计软件实现，如R软件的“survival”包、SAS、stata、SPSS等。章仲恒等[15]介绍了利用R语言执行时依性Cox模型的具体步骤，有兴趣的读者可参考，此处不再赘述。

(2)时依性Cox模型的优势和局限性

与界标分析不同，时依性Cox模型纳入了时依性的协变量，允许患者分组随时间改变，充分利用了所有患者的随访信息，具有更高的统计效能。时依性Cox模型得到风险比的估计，可以定量的表示时依性协变量对结局的影响。此外，当含有多个时依性协变量，并且协变量的取值随时间的变化不止一次时，时依性Cox模型同样适用。

时依性Cox模型的局限性包括：首先，时依性的Cox模型通过风险比解释时依性协变量对结局事件的影响，缺少生存曲线图形化的直观呈现。其次，由于时依性协变量的存在，风险比例模型在t=0时的轨迹是未知的，不能简单地根据风险计算生存概率，这就意味着时依性Cox模型丧失了预测的功能。当基于具有时依性的协变量进行预测时，界标分析可能更加适用[16]。此外，由于时依性协变量通常伴随着混杂因素，因此时依性Cox模型很难探究其中的因果关系。关于其中的数理机制，Fisher和Lin[17]进行了简要的阐述。

3.逆概率加权

(1)逆概率加权简介

逆概率加权是一种基于倾向性评分(propensity score)[18]的统计方法，是处理观察性数据的强有力工具。倾向性评分是指患者进入暴露/处理组的概率，常用于控制已观测的混杂因素，郭申阳等对倾向性评分进行了详细的介绍[19]。

利用逆概率加权进行统计分析，首要的一步就是构建倾向性评分估计模型。在清晰地了解某种疾病的发展进程或治疗过程后，以患者临床、人口学、预后和治疗特征等作为预测变量，构建多因素的倾向性评分估计模型，如logistic回归，使得每个患者在随访的每个阶段，都会产生一个进入试验组的概率估计值。然后利用第一步产生的概率估计值的倒数作为权重进行加权，构建逆概率加权模型。这些权重，部分地消除了由于未随机化分组产生的偏倚。

在构建倾向性模型时，需要满足一个重要的假设：无遗漏的未观测混杂因素[20]，即所有的混杂因素都考虑在内。因此，在研究中，需要尽可能全面地考虑所有会影响到干预与结局关系的混杂因素。

(2)逆概率加权的优势和局限性

由于时依性暴露/处理的存在，研究分组缺少了随机化的过程，使得非暴露/对照组和暴露/处理组间存在混杂因素。通过逆概率加权，使得各组的基线数据更加均衡，具有可比性。逆概率加权也使用了所有的患者数据，具有较高的统计效能。逆向概率加权还可以处理删失数据[21]，例如在Cox模型的框架下通过逆概率加权方法来估计存在删失的协变量的效应[22]。此外，Agogo[23]提出了基于逆概率加权的共享参数联合模型(IPTW-weighted joint model)，来估计纵向测量数据对二分类结局的效应，有效地控制了混杂因素。

但是，逆概率加权只是部分控制了各组间的混杂因素，一定程度弥补了缺少随机化的不足，不可能完全替代随机化步骤，可以作为界标分析、时依性Cox模型的补充方法。并且，逆概率加权在软件实现上更具有挑战性，Van der Wal[24]等介绍了如何使用R软件包“ipw”实现逆概率加权。

模拟研究与实例分析

我们将Cox模型、界标分析和时依性Cox模型，在R软件包“JM”中的原发性胆汁性肝硬化(PBC)数据集[25]中进行应用，来比较上述方法处理未亡时间偏倚的效果。PBC数据集纳入了312名原发性胆汁性肝硬化的患者，包括患者的一般情况(年龄、性别)、用药情况、症状体征(肝肿大、腹水、蜘蛛痣)等。比较出现腹水的PBC患者与非腹水PBC患者的生存情况。将年龄、性别、用药情况和是否有腹水，分别纳入Cox模型、界标分析和时依性Cox模型进行分析。由于腹水是肝硬化失代偿期产生的体征，而PBC失代偿期从发病到确诊平均为27个月[26]，因此在界标分析中，选取tLM=2作为界标时间，分析结果如表1。

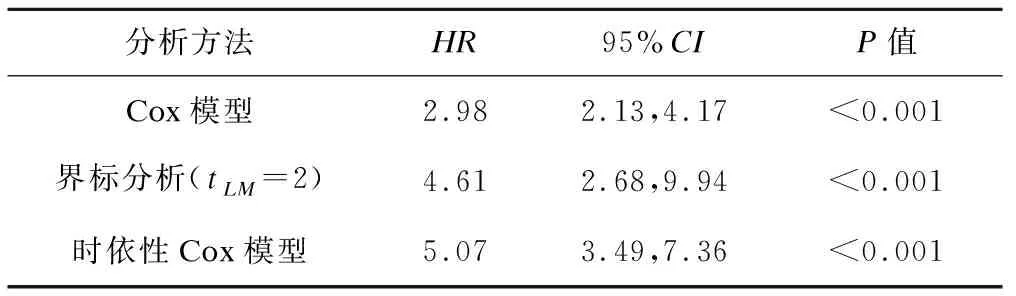
表1 出现腹水对原发性胆汁性肝炎化患者死亡风险影响分析结果

由表1知，由于腹水是PBC患者晚期出现的症状，从确诊到出现腹水需要经过一段“未亡时间”，由于Cox模型受到未亡时间偏倚的影响，低估了腹水组PBC患者死亡风险(HR=2.98)。界标分析和时依性Cox模型，在一定程度上校正了未亡时间偏倚，得到了较为准确的结果。其中部分腹水患者，早期无腹水，产生腹水后，经过治疗体征消失，时依性Cox模型准确分析了每一段产生腹水的时间，因此得到了较大的风险比。此外，Cox模型和界标分析以可视化的形式展示，生存曲线分别见图1和图2。统计分析使用了SAS 9.4、R软件。

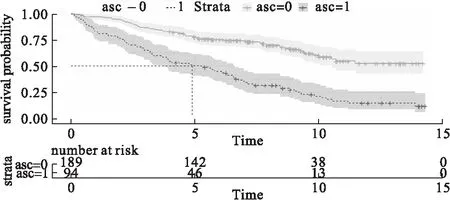
图1 腹水与非腹水PBC患者Cox模型生存曲线

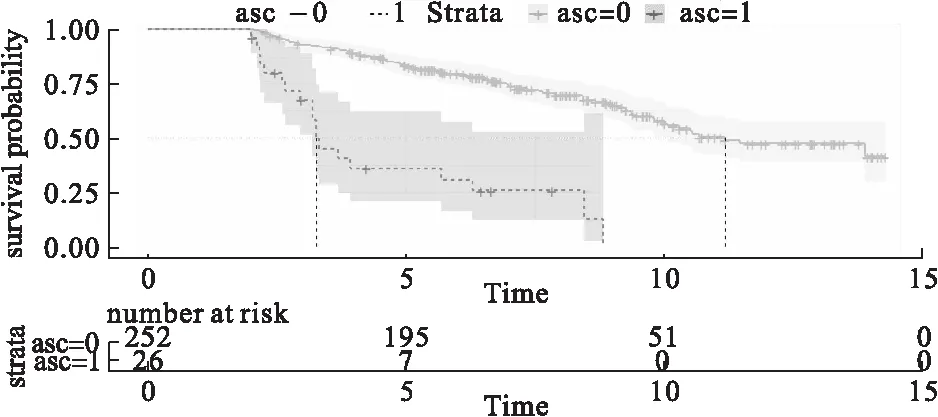
图2 腹水与非腹水PBC患者界标分析生存曲线

总结及展望

本文介绍了几种常用的未亡时间偏倚处理方法，包括界标分析、时依性Cox模型以及逆概率加权。界标分析是处理未亡时间偏倚较为有效的方法，它以直观性、简便性的特点在医学研究中被广泛应用。时依性Cox模型可以通过风险比的估计定量地描述时依性协变量对结局的影响。IPW可以作为界标分析的替代和补充方法。三种方法的特点总结见表2。

表2 处理未亡时间偏倚的常用统计方法比较

近几年，统计学家提出了更多的处理方法，或多种方法综合使用，对未亡时间偏倚的处理日趋成熟。M.A.Nicolaie[11]等构建了界标分析的超级模型(supermodels)，将界标分析进行拓展，对竞争风险中含有时依性协变量的问题进行动态预测。对于不能在任意时刻测量的内生性时依性协变量，提出了纵向生存数据的联合模型(joint models)[25]，并且允许测量误差的存在[16]。在一项关于冠脉造影和不良结局关系的研究中，Pierluigi Tricoci等[27]同时使用了IPW和界标分析，部分地弥补了界标分析缺少随机化属性的缺陷。

然而，当时依性变量满足以下条件时：随时间变化、是结局的影响因素、受到前一次干预的影响又会影响后一次的干预，则称之为时依性混杂。存在时依性混杂的情况下，需要进行因果推断，则需要通过其他的方法处理，如构建边缘结构模型(marginal structural model，MSM)[28]。

随着循证医学的不断发展和人们对医学研究认识的完善，未亡时间偏倚逐渐受到越来越多的关注，在处理时依性自变量、时依性混杂因素方面，将会有更多、更先进的方法提出，以消除其产生的偏倚。本文仅对处理未亡时间偏倚的常用统计方法进行了综述，并进行了实例分析，尚需进一步的研究，对这些处理方法的适用条件、稳健性、效能进行定量的比较。