南京市细菌性痢疾时间变化特征及趋势预测*
2022-03-17南京市疾病预防控制中心210003许阳婷
南京市疾病预防控制中心(210003) 许阳婷
【提 要】 目的 分析南京市1951-2019年细菌性痢疾流行变化特征,为细菌性痢疾的防控提供依据。方法 运用移动平均、joinpoint分析和小波分析方法,对南京市1951-2019年细菌性痢疾年发病率时间变化进行分析。结果 细菌性痢疾发病率在南京市整体呈下降趋势,5年移动平均曲线呈现先台阶式后滑道样线形下降。joinpoint分析显示平均年度变化百分比为-5.60,细菌性痢疾流行过程中有3个转折点,分别在1965年从升到降、1968年由降到略升和1984年下降。Morlet小波法时频分析小波系数实部和模方显示12和31为2个中心尺度,呈现的周期为20年和38年。小波方差显示有2个主周期,第一主周期在31尺度。从细菌性痢疾的周期、趋势分析结果看,目前南京市进入细菌性痢疾高发周期中。结论 依据细菌性痢疾的变化特征,当前应该加强对细菌性痢疾的监测,及时做好疫情处置。
细菌性痢疾(bacillary dysentery)是由志贺氏疾病杆菌引起的一种急性肠道传染病,人群普遍易感,病后免疫力持续时间短暂,不同型别菌株间无交叉免疫,缺乏有效的疫苗免疫。其发病率居于我国法定乙类报告传染病的前5位[1]。因而有流行范围广、传播速度快、对健康危害大等特点。南京地处中国东部、长江下游、北亚热带湿润气候,春秋短、冬夏长,四季分明,雨水充沛,相对湿度76%[2]。此地理气候条件适宜志贺菌属的繁殖与传播。有研究显示,近年南京市有些地区细菌性痢疾年均发病率维持在10/10万以上[3]。本文通过对南京市1951-2019年69年来细菌性痢疾发病率趋势变化和周期等特征的分析,为南京市细菌性痢疾防控、合理资源配置提供理论支撑。
资料与方法
1.资料来源
1951-2000年细菌性痢疾发病率资料来源于南京市卫生防疫站年报,2001-2003年细菌性痢疾资料来源于南京市疾病预防控制中心年报,2004-2019年病例资料和人口学资料来源于“中国疾病监测信息系统”的病例报告系统和基本信息系统,发病数按发病时间导出。
2.方法
主要用小波分析和joinpoint方法对细菌性痢疾发病特征、趋势、周期、突变点等变化进行详细的分析;
(1)移动平均
指定时间段,对时间序列数据进行移动计算平均值。即x的n移动平均值:
(2)joinpoint模型[4]
通过模型拟合将一个长期趋势线分成若干有统计学意义的趋势区段,各段用连续的线形进行描述[5]。y为年份,Ry为该年份发病率,表达式为:
log(Ry)=b0+b1y
b0为截距,b1为回归系数,反映各时间段内发病率的趋势变化[5]。用t检验判断总体回归系数是否为0,即趋势变化是否有统计学意义。平均年度变化百分比(average annual percent change,AAPC)[5]和年度变化百分比(annual percent change,APC)[5]表达式如下:
(3)小波分析
小波分析(wavelet analysis)亦称多分辨率分析(multiresolution analysis)[6],用Morlet小波进行时-频小波分析
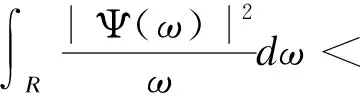
其中,a为频率参数(亦称尺度因子),b为时间平移参数(亦称平移因子);Δt为取样时间间隔;n为样本数[10]。
(4)小波方差分析
将小波系数的平方值在b域上积分,就可得到小波方差,公式如下:
var(a)=[ωf(a,b)]2
其随尺度a的变化过程,即为小波方差图[11]。
3. 统计分析
应用Excel 2007对数据进行整理、制表及分析,用Joinpoint Trend Analysis Software 4.8.0.1和MATLAB 2008b软件进行发病率趋势、变化点和周期分析;小波方差检验水准为α=0.01,Joinpoint检验水准=0.05。

表1 南京市1951-2019年细菌性痢疾发病率年内分布情况
结 果
1.细菌性痢疾发病率年内各月发病情况
年内细菌性痢疾发病呈现夏秋季单峰,季节聚集性明显,占年内发病构成的70.74%,冬春季为低发病期。
2.细菌性痢疾发病率年际发病情况
各年发病率呈下降趋势,发病率5年移动平均曲线呈现先台阶下降,后滑梯形下降。1951-1966年为高发病年,发病率在高位波动,年平均发病率为378.95/10万;1970-1984年为中发病年,年平均发病率为262.00/10万;随后一路下降,2014年以来发病率维持在5/10万上下波动,见图1。joinpoint分析显示1951-2019年发病率AAPC为-5.60,呈下降趋势,出现3个转折点,分别在1965年、1968年和1984年,其中1965-1968年发病率年度变化无统计学意义(t=-1.20,P=0.30>0.05),见图2和表2。

图1 南京市1951-2019年细菌性痢疾发病情况
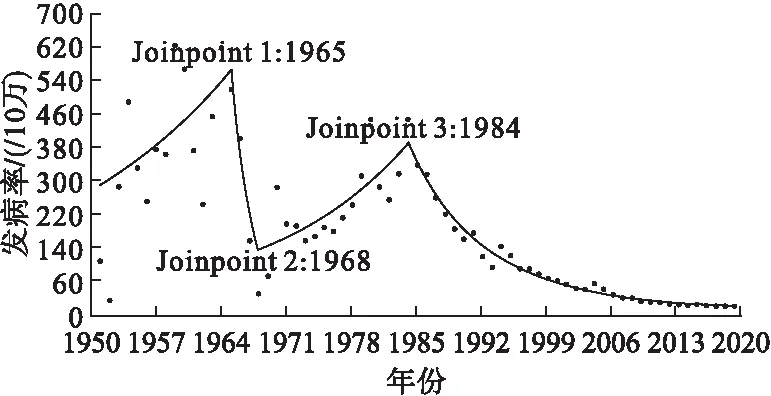
图2 南京市1951-2019年细菌性痢疾发病率joinpoint变化图

表2 南京市1951-2019年细菌性痢疾发病率趋势分析
3.细菌性痢疾年发病率序列的时频分析
对南京市1951-2019年发病率时间序列进行 Morlet 小波变换后的小波系数实部等值线图,见图3,图中小波系数0等值线为突变点;小波系数正值等值线为高发病年份;0等值线外空白区是小波系数负值区为低发病年份。由图3可以看出,有二个周期震荡,分别在8~15和25~32时间尺度,尤其在25~32时间尺度上,发病率有3个偏多周期和3个偏少周期。模方图中(图4)在相同两个时间尺度上也表现出了周期现象,特别在25~32时间尺度上周期表现的非常明显,出现的时间大约为1951-2010年。两个周期中心分别在12和31时间尺度上。从主周期不同的时间尺度变化趋势可见(图5),在12时间尺度上,呈现3个周期变化特征,周期约为20年左右;在31尺度上,呈现两个周期变化特征,周期约为38年左右。两个主周期时间尺度都显示当前发病处在高发病区域。
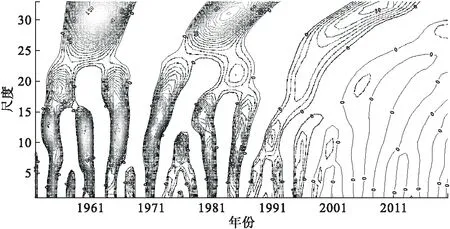
图3 南京市1951-2019年细菌性痢疾发病率小波系数实部等值线图

图4 南京市1951-2019年细菌性痢疾发病率小波系数模平方等值线图
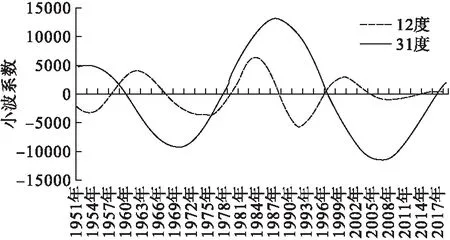
图5 南京市1951-2019年细菌性痢疾发病率小波系数实部多时间尺度变化趋势
4.细菌性痢疾发病率序列的主要周期分析
在小波模方差曲线出现了2个较明显的峰值,见图6,方差值由大到小依次对应的尺度为31和12。其中,曲线的最大峰值对应的尺度为31,说明整体发病率变化31时间尺度上周期震荡最明显,为第一主周期尺度;结合模方图(图4)可见,31尺度上的周期震荡在整个时间序列上表现非常明显。

图6 南京市1951-2019年细菌性痢疾发病率小波方差
讨 论
南京市1951-2019年细菌性痢疾的发病率从500/10万左右到5/10万左右,经历了三个转折变化点,分别为1965年的下降,1968年的上升和1984年的下降过程。发病情况与国民经济的增长、居民收入的提高等社会经济发展因素,基本卫生服务的水平提高及环境卫生条件改善密切相关。这与刘东立等人的报道一致[12-13]。
流行病学常用时间序列来研究疾病发生发展的过程。时间序列是由时域和频域组成。目前在研究疾病发生发展过程中常用的分析方法多是要求时间序列为平稳序列,平稳是对于频域提出的要求,疾病的发生发展随时间的变化往往受病原体、环境、人群和政策等多因素的综合影响,呈现的疾病时间序列多为不平稳序列。这种不平稳除表现在趋势、周期性上,还表现在随机性和突变性上,形成“多尺度”结构,具有多层次演变规律[14]。对非平稳时间序列的研究,通常需要某一频段对应的时间信息,或某一时段的频域信息。然而,单独时域分析和频域分析对此均无能为力[14-16]。20世纪80年代初,由Morlet提出的具有时-频多分辨功能的小波分析,为研究时间序列问题提供了可能,将隐藏在时间序列中的多种变化周期,通过不同时间尺度将时间序列的变化趋势充分地反映出来,并能对未来发展趋势进行定性评估[17-19]。小波系数实部等值线图是在时域中呈现出不同时间尺度的年发病率时间序列周期变化情况,可以用于推断年发病率的未来变化趋势。模方相当于小波能量谱,能量谱展示出不同时间尺度的周期变化。从小波方差分析主周期趋势图中可以得到不同的时间尺度下[19],发病率存在的平均周期及高-低发病率情况的变化特征。
