试验序贯分析原理及其在meta分析中的应用*

安徽医科大学公共卫生学院流行病与卫生统计学系(230032)

邵 明 陈雨婷 许 伟 杨 会 邹延峰 范引光 潘贵霞 潘发明△

【提 要】 目的 介绍试验序贯分析(trial sequential analysis，TSA)原理以及在meta分析中的实际应用，并探讨不同参数设置对TSA结果的影响。方法 相对危险度减少率(relative risk reduction，RRR)作为TSA分析的重要估计参数，比较不同设置方法下的结果。结果 公式法TSA的结果显示，Z曲线已经越过TSA边界，认为meta分析的结果是可靠的，然而假设法仅仅越过了传统边界，也没有达到期望的信息量(required information size，RIS)，无法得出稳健的meta分析结果。结论 本文揭示了不同RRR参数导致的不同TSA结果，公式法在TSA分析中的应用值得研究。

meta分析，又称荟萃分析，作为计算多个相同研究主题合并后效应量的一种统计学方法，其优势不仅扩大了样本量，还增强了结果的精确性和稳健性。目前，公认的基于随机对照实验(randomized controlled trial，RCT)的meta分析是级别最高的证据，已经被广泛用于疾病的诊断、治疗、预后以及流行病学研究中。然而，随着新的研究纳入，meta分析不断被更新，有证据显示反复把P<0.05 认为存在统计学差异，进行差异性检验，犯I类错误(假阳性)的概率在10%～30%之间[1-3]。随着各种不断更新的meta分析日益增多，因重复性检验而增加I类错误的概率也越来越大，因此对同一个研究主题的统计分析结果的稳定性受到了很多学者的关注[4-5]。

为了最大程度降低因纳入新的研究而反复性假设检验增加的风险，试验序贯分析(trial sequential analysis，TSA)的方法在1997年被Pogue等人引入meta分析中，克服了传统meta分析存在的不足之处，使统计分析结果更具有稳健性。此外，TSA还可以估算出meta分析得到稳定的结论所期望的信息量(required information size，RIS)，即为临床试验提供了一个达到样本量的终止标准。不仅如此，TSA还提供一个无效假设标准，可以克服某一研究主题真实效应的确不存统计学差异而meta分析在不断反复更新无法及时终止的缺陷。国内已有学者对TSA方法进行了介绍，同时也有详细的案例[6-10]，但是都没有很好地阐述TSA软件参数的设置，尤其是相对危险度减少率(relative risk reduction，RRR)的设置，国内外很多篇引入TSA的meta分析都没有明确提出RRR设定[11-14]，因此TSA本身的分析结果可能存在一定偏差，导致meta分析结果被错误定义为稳定的结论。本文主要目的是介绍TSA基本原理并结合实例介绍如何使用TSA软件，以及在不同参数设置下对TSA结果的影响。

TSA基本原理

1.TSA简介

序贯分析(sequential analysis，SA)最早出现在1947年，由美国统计学家亚伯拉罕·瓦尔德(Abraham Wald)首次提出用于解决军需品的质量检验。在研究某一决策性问题时，对需要的样本数量事先不进行预设，而是通过逐次取少量样本进行检验，直到获取到足够的信息做出决策停止，这样的方法极大地节省了样本量，据估计可以减少约30%～50%的样本[15]，此外某些情况下，达到预期结论的可靠度及精确度必须采用序贯分析。尤其一些大型研究，无法一次性获得足够的样本，需采用陆续试验和分析的方式，由于序贯分析可以提前得到信息，因此对于一些有效的干预措施能够在试验未结束前及时推广，同时对得到无效结论的试验立即终止。

鉴于序贯分析在大型随机对照试验中的优越性，序贯分析在1997年被引入meta分析中，最大程度减少前期meta分析不精确和重复性检验带来的早期假阳性错误。此外，在单次临床试验前都需要对样本量进行估算，因此meta分析也需要对纳入研究数目合并后的样本量进行估算，以期获得足够的RIS。TSA就提供了这样一个估算，TSA在meta分析中将各研究按照年份顺序依次纳入，不仅计算出RIS，还提供了假设检验的界值和无效线。

2.meta分析与TSA信息量估计

TSA有利于二分类数据和连续性数据的meta分析。无论哪一类数据，都存在多种指标可用于干预效应比较。

对于分类数据，两组的干预效应常用相对危险度(relative risk，RR)、比值比(odds ratio，OR)、特异危险度(rate difference，RD)[16]来表示，公式如下：

公式中NA和NB分别表示在A和B两组中进行若干次独立试验次数，某一事件在A和B中发生的次数分别为EA和EB，而对于连续数据在进行meta分析时一般采用加权均数差(weighted mean difference，WMD)和标准化均数差(standard mean difference，SMD)[4]，公式如下：

公式中Wi表示权重系数，mA，mB，SA，SB分别表示某一指标在A和B两组的均数和标准差；WMD用于度量衡单位相同的连续性变量，SMD则用于研究度量衡单位不同的和均数相差较大的连续性变量。

一般认为，一个确凿可靠的meta分析所需要的样本量大小至少要和一个大型的、设计合理的和有把握的干预试验一致，在此条件下计算meta分析所需要的信息量，计算公式如下：

RIS=2(Z1-α/2+Z1-β)2·2·σ2/δ2

公式中α为I类错误的最大风险，β为II类错误的最大风险；Z1-α/2和Z1-β分别表示1-α/2和1-β的标准正态分布分位数；对于二分类变量δ=PA-PB(PA和PB分别表示某一结果在A和B组占比)[17]；对于连续性变量δ表示A和B组方式差异的预先估计[18]；б2表示相关联的方差。

在进行TSA时，对于二分类变量一般采用PA=(PB-RRR)来对干预组的期望事件比例进行计算即可，因此PB和RRR的设定要尽可能接近真实值。此外，meta分析的统计学意义使用的是Wald-type检验统计量[19-20]，通常被称为Z-value，每当更新一次meta分析，Z值也会被重新计算，因此随着meta分析的不断更新，会产生一系列Z值，从而产生一个曲线，即Z-曲线[21]。对该Z值的校对被称为监测界值，在meta分析中具有的一系列临界值，被称为试验序贯监测界值(TSA边界)，因此meta分析和试验序贯监测界值结合即为试验序贯分析[22-23]。

3.TSA结果的解释

如图1，Z曲线随着纳入样本量增加将出现的四种情况。Z1曲线超过了传统边界(P<0.05，Z=1.96)，但是没有越过TSA边界，提示有可能犯假阳性错误；Z2曲线与TSA边界相交，提示meta分析结果具有稳健性，即使没有达到RIS；Z3曲线与传统界值和TSA界值均未相交，尚不能得出阳性或者阴性结论；Z4曲线与无效线相交，提示没有意义。

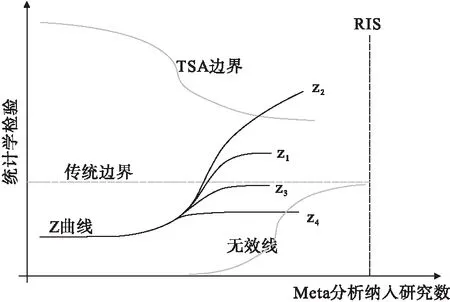
图1 试验序贯分析结果举例解释

RRR设定与探讨

1.TSA软件安装与启动

TSA软件是一款基于JAVA(https：//www.java.com)语言环境运行的程序，可以在任何支持JAVA语言的操作系统上运行。TSA软件是由丹麦哥本哈根的哥本哈根临床试验中心(Copenhagen Trial Unit)开发，并提供一份TSA工作者手册(User manual for TSA)[24]。TSA软件免费下载地址为www.ctu.dk/tsa。下载完成后会得到一个压缩包，读者自行进行解压到指定盘符的文件夹下，顺利安装JAVA后打开。

2.TSA软件参数的设置

打开TSA软件后，可以导入Revman数据或者人工录入数据，翁鸿等[10]对TSA软件操作界面介绍的非常详细，这里不再做重复赘述，本文主要对“Alpha-spending Boundaries”内部参数设置进行介绍。这里是TSA界值设置界面，第一步“Name”设置为“RIS”，在假设检验边界类型(boundary type)勾选双侧检验(Two-sided)；第二步“Type 1 Error”设定5%，在信息轴(Information Axis)勾选“Sample Size”，勾选“Apply Inner Wedge”激活“Power”设定为80%；第三步“InformationSize”勾选“Estimate”。关于RRR值的设定，目前的文献报道总结有三种，第一种是作者预先假设10%、20%、30%等；第二种是根据临床经验进行估算；第三种则是作者根据纳入研究的meta分析结果计算。异质性校正(Heterogeneity Correction)这里勾选“Model Variance Based”；最后点击“Add”，再点击Calculations模块中的“Perform calculations”，开始运算。

3.基于二分类变量的TSA案例演示

本文以《Association between IL-17A and IL-17F gene polymorphism and susceptibility in inflammatory arthritis：A meta-analysis》一文为例[25]，探讨不同假设参数设置下TSA结果的影响。我们以“基因多态性”、“试验序贯分析”“TSA”为检索词检索数据库，截至目前为止发表的有关基因多态性与疾病相关性研究的meta分析涉及TSA的文献共计16篇，其中仅2篇中文。6篇文章假设RRR为20%，1篇文章假设RRR为10%，8篇文章没有在文章中明确提出参数的设置，只有1篇文章较为精确地对RRR参数设置进行了详细描述[26]。有关RRR的估算我们介绍两种，对于队列研究RRR=1-RR，对于病例对照研究可以近似认为RRR=1-OR，然而无论是RR还是OR都取决于meta分析纳入文献的质量，因此也存在一定程度上的误差，这里我们认为可以选取高质量的文章进行计算得出RR或者OR[24]。在本文例子中，我们可以发现OR=0.64(图2)，因此RRR应该设置为36%进行TSA分析，此外我们按照现有研究的假定考察了RRR设定为10%和20%的TSA分析结果。

图2 白细胞介素17基因多态性与自身免疫性疾病关联性的森林图

4.TSA分析结果

如图3、图4所示，Z曲线没有去TSA边界相交也没有越过RIS，得出的结论将会是当前的meta分析结果将很可能存在假阳性的错误，仍然需要后续的研究进一步验证。图5显示Z曲线虽然没有越过RIS但是却与TSA边界相交证明了此meta分析结果具有一定的稳健性。这两种不同结果出现的原因就在于RRR参数的设置不同，前者可以认为是人为对RRR进行假设，后者是通过我们给出的公式(RRR=1-OR)获得，前文提到二分类变量的RIS的计算RRR会直接影响PA，因此不同的RRR值会影响TSA结果。然而无论是假设法、经验法还是公式法，都应该结合具体的事件来使用，因为我们目的是尽可能的得到最接近真实的RRR。本案例是一个单核苷酸多态性的meta分析，然而在临床上并没有对某个位点在对照组中突变的估计，只能通过假设和公式法进行，虽然假设法相比于公式法显得直接，但是公式法又取决于纳入文献的质量，在某种情况下假设法不失为一个有效的方法。当然在三种方法都可以使用的前提下，我们应该优先使用经验法，因为Pogue和Yusuf的文章就是经验法的一个很好案例[20，27]。

图3 RRR假设10%的TSA分析结果

图4 RRR假设20%的TSA分析结果

图5 RRR估算为36%的TSA分析结果

TSA展望

目前，已发表的meta分析中涉及TSA方法的国外研究(主要是英文)不足100篇文献，而国内以“试验序贯分析”和“meta分析”或者“荟萃分析”在中国期刊全文数据库(CNKI)进行检索，仅发现45篇，其中2019年与2020年共计发表含有TSA的meta分析文献数目为29篇，国内最早记录是2011年在《中华高血压杂志》上发表的《抗高血压药物与罹患癌症的风险：324168例参与随机临床试验病人的荟萃分析和试验序贯分析》[28]。尽管近两年发表数目增加，在有记录以来的发表总数中占比64.4%，但是很少有研究者对TSA参数的设置进行详细描述，很多都是假设性地进行TSA分析，当然也有研究者对参数设置进行了详细描述，RRR值设置以meta分析结果(RR或者OR值)进行计算[29]。

前文所述，TSA能够克服传统meta分析的不足之处，能够有效节省不必要的继续试验，不仅如此其在网状meta和系统评价中也有非常不错的应用前景。然而随着涉及TSA的meta分析不断增多，有关TSA参数设置的规范也应当引起研究者们的重视，不同参数下得到的TSA结果大相径庭，三种方法的使用应该结合实际情况具体分析。此外，TSA在meta分析中虽能够有效的支持结论，但是TSA在以严格的控制假阳性错误(I类错误)为主的同时也会增加假阴性风险(II类错误)的可能性，因此在使用TSA方法时应该慎重。