长期荷载作用下圆端形钢管混凝土力学性能

廖仁生，李永进，刘文华，张铮

(1. 福建江夏学院 工程学院，福建 福州 350108；2. 福建农林大学 交通与土木工程学院，福建 福州 350002；3. 福建工程学院 教学与质量管理办公室，福建 福州 350118)

圆端形钢管混凝土柱在长期荷载作用下，钢管内混凝土会发生徐变和收缩[1]，引起构件位移增大、内力重分布、刚度降低，从而对圆端形钢管混凝土柱的整体力学性能产生较大影响。圆端形钢管混凝土轴压、偏压、偏拉等方面已有较多学者进行研究[2-6]，但考虑长期荷载作用下圆端形钢管混凝土力学性能的相关报道较少。

由于桥梁的使用年限较长[7]，圆端形钢管混凝土柱作为桥梁结构的主要承力构件[8-10]，长期荷载对其影响不容忽视。为此，本文通过有限元分析法，对圆端形钢管混凝土柱在长期荷载作用下的力学性能进行研究。

1 有限元模型建立

1.1 混凝土和钢管材料本构模型

1)长期荷载作用阶段混凝土本构模型

长期荷载作用下混凝土徐变收缩效应明显，采用文献[11]提供的三维黏弹性本构模拟此阶段的混凝土，其应力-应变关系可表示为：

(1)

式中参数含义详见文献[11]，该模型中，还需确认的核心混凝土最终徐变系数φu=0.9[12]。

2)承载力分析阶段混凝土本构模型

长期荷载作用阶段结束后进入承载力分析阶段，采用文献[11]提供的塑性损伤本构来模拟此阶段的混凝土，其长期荷载作用影响时的应变εt和对应短期荷载作用下应变ετ0关系可表示为：

εt= [1+φ(t,τ0)]ετ0+εsh

(2)

式中εsh=5.36×10-4[13]。

3)钢材本构模型

钢材的本构模型采用二次塑流模型，弹性模量E=2.06×105MPa，泊松比v=0.3。

1.2 有限元模型

圆端形钢管混凝土柱构件有限元模型中钢管和混凝土分别采用壳单元(S4R)和实体单元(C3D8)，混凝土和钢管的接触面有法向和切向接触，分别用硬接触和库伦摩擦模型进行模拟，其中库伦摩擦系数取0.6[13]。为确保端板和钢管之间不发生相对运动，采用*Tie接触将两者连接在一起。

柱构件的加载方式为，长期荷载作用阶段时，在上端板x轴方向施加恒定的长期荷载NL，当长期荷载作用结束时，在上端板处施加位移荷载，直至构件破坏，进而获得长期荷载作用下的圆端形钢管混凝土荷载-应变全过程曲线。在有限元模型中，限制柱下端板x、y、z轴的所有自由度，柱上端板限制除x轴平动自由度之外的5个自由度，并在x轴平动自由度上施加长期荷载NL和长期荷载作用结束后的位移。

1.3 模型验证

根据上述建模方法，建立长期荷载作用下的圆端形钢管混凝土柱有限元数值模型，将数值分析结果同已有的长期荷载作用下的圆形钢管混凝土试验数据[14]和短期荷载作用下的轴压圆端形钢管混凝土试验数据[15]进行对比，对上述建模方法进行验证，试验结果和计算结果对比曲线见图1。

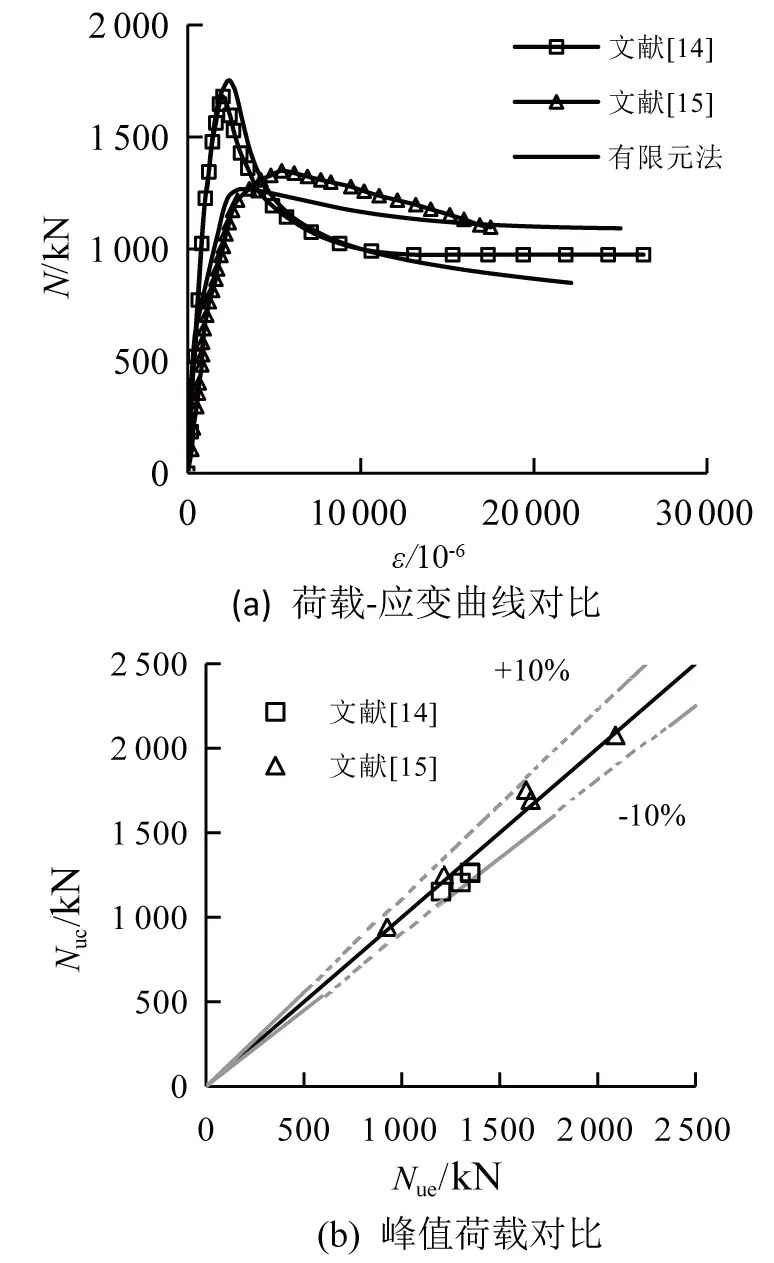
图1 试验结果和计算结果对比曲线

从图1(a)(b)可看出，有限元计算所得荷载-应变曲线同试验所得曲线吻合程度较高，数值模型计算峰值荷载同试验值误差均在10%以内。通过长期荷载作用下的圆形钢管混凝土试验数据、短期荷载作用下的圆端形钢管混凝土的轴压试验数据，验证了模型的合理性，基于此模型，可进行长期荷载作用下的圆端形钢管混凝土柱力学性能研究。

2 有限元模型分析

采用上述建模及有限元分析方法，可得圆端形钢管混凝土在长期荷载作用下的荷载-应变曲线，对其受力全过程进行分析，基本参数：圆端形钢管截面长边边长D为1 600 、800 、1 200 、2 000 mm；圆端形钢管截面短边边长B=800 mm；长细比λx=22；C50混凝土；Q355钢材；含钢率αs=0.1；长期荷载比n=NL/Nu=0.4(NL长期荷载，Nu极限荷载)，长期荷载持荷年限为50 a。

2.1 荷载-应变全过程分析

图2给出了长期荷载作用下圆端形钢管混凝土的荷载-应变全过程曲线，其中A、B、C、D分别代表长期荷载开始作用时、长期荷载结束作用时、达到峰值荷载时、峰值荷载下降至85%时。图中还分别给出在受力全过程中圆端形钢管混凝土钢管、平直段和圆弧段混凝土各自的承载力变化情况。在长期荷载作用下，平直段混凝土荷载卸载了23.9%，圆弧段则卸载了24%，钢管承担荷载增加了38.7%，从数字上体现了混凝土卸载的部分全部转由钢管承担。

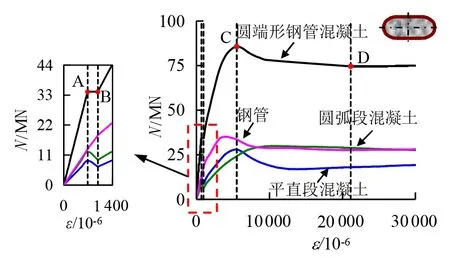
图2 长期荷载作用下圆端形钢管混凝土荷载-应变曲线

如图3所示，考虑长期荷载的影响下，构件的峰值荷载由85 562 kN增加到了85 703 kN，峰值荷载增幅0.17%，几乎没有变化。峰值荷载对应应变由3 285增加到了5 527，增幅68.25%，峰值荷载对应应变增幅68.3%，显著增大，亦即考虑长期荷载后，柱构件的刚度明显降低，而延性显著增强。

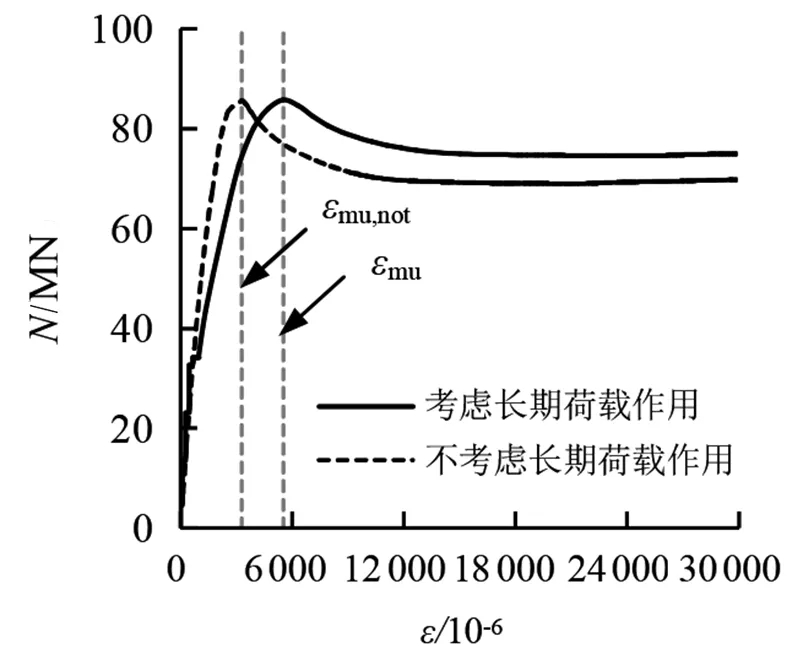
图3 考虑长期荷载与否荷载-应变曲线

2.2 高宽比影响分析

图4给出了考虑长期荷载作用与否的峰值荷载、峰值应变和高宽比的关系曲线。高宽比(圆端形钢管截面长边边长/圆端形钢管截面短边边长)为1～2.5时，考虑长期荷载情况下，对应极限荷载增幅范围为0.2%～3.2%，长期荷载作用对构件的极限荷载无明显影响，从曲线中还可看出，随着高宽比增大，圆端形钢管混凝土的极限荷载大幅提升。高宽比1～2.5时，考虑长期荷载情况下，对应峰值应变增幅范围为68.3%～98.5%，高宽比增大，峰值荷载对应应变先大幅下降，而后趋于稳定，长期荷载对构件的延性性能影响显著，随高宽比的增大，增长幅度逐渐降低而后趋于平缓。

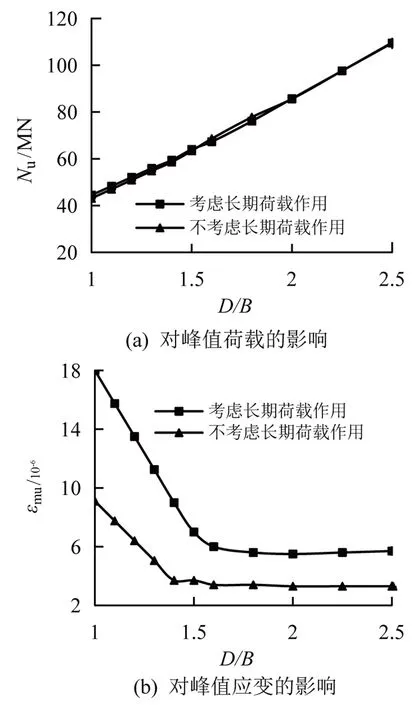
图4 考虑长期荷载与否对不同高宽比钢管混凝土柱的峰值荷载及峰值应变的影响情况

2.3 混凝土截面应力分析

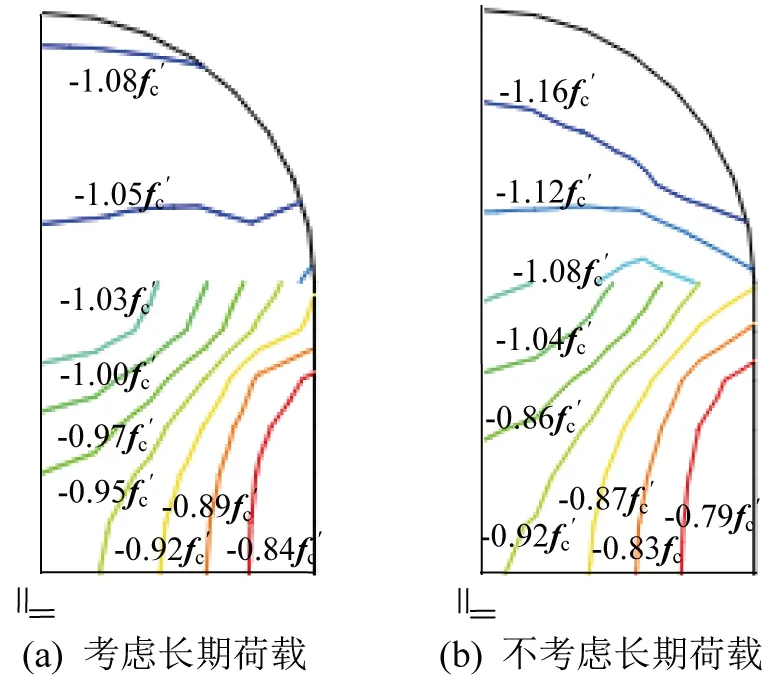
图5 考虑长期荷载与否混凝土截面应力(1/4截面)

2.4 钢管应力分析

图6给出了长期荷载作用与否的钢管关键点(圆弧段1点和平直段2点)的纵向应力(σ11)、环向应力(σ22)、Mises应力(σM)变化曲线，从图6可看出，未达到屈服强度前，钢管的σ11和σM的增长速度快于σ22，达到屈服强度后，钢管σ11和σM的增长速度趋于平缓，σ22继续增长；进入强化段后，钢管σM和σ22缓慢增长，σ11减小后缓慢增长。从图6可得，钢管和混凝土之间的σ22影响σ11；在C点，考虑长期荷载作用的钢管纵向应力高于不考虑长期荷载的情况，长期荷载作用下混凝土卸去的纵向应力由钢管承担；而从曲线后续的发展趋势中可看出，长期荷载对钢管应力值影响不大。

图6 考虑长期荷载与否钢管应力-应变曲线

2.5 接触应力分析

图7为D/B=2时，考虑长期荷载作用与否的圆端形钢管混凝土，其钢管和核心混凝土的接触应力-应变曲线。由图7可得，圆端形钢管混凝土平直段的接触应力明显小于圆弧段，钢管对混凝土的平直段约束力较弱。从图中还可看出，长期荷载的作用，延缓了钢管和混凝土之间最大相互作用力的出现时间，但对接触应力值无明显影响(P2无明显应力值)。

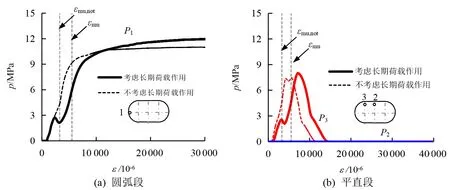
图7 考虑长期荷载与否接触应力-应变曲线

3 结论

1)通过有限元分析了圆端形钢管混凝土轴压柱在长期荷载影响下的工作机理，可知长期荷载对峰值荷载影响不明显，对构件延性性能影响显著。

2)随着高宽比的增大，构件的刚度和极限荷载随之增大，延性性能下降。

3)钢管对混凝土圆弧段的约束力要强于平直段，相较于不考虑长期荷载圆端形钢管混凝土峰值荷载点对应的纵向应力，混凝土的纵向应力降低，钢管的纵向应力增大。

4)在长期荷载的影响下，延缓了跨中截面钢管和混凝土最大相互作用力出现的时间，但对接触力值影响不大。