6061铝合金热变形行为与热加工图

2022-03-17王海龙梁卫抗王乾廷林光磊

福建工程学院学报 2022年1期

王海龙，梁卫抗，王乾廷，林光磊

(1.福建工程学院材料科学与工程学院，福建福州 350118；2.福建省新材料制备与成形技术重点实验室，福建福州 350118；3.福建省精确成型制造工程研究中心，福建福州 350118 ；4.福建省南平铝业股份有限公司，福建南平 353000)

本研究基于Gleeble-3500热模拟试验机平台，开展6061铝合金的等温热压缩实验，根据实验数据建立了双曲正弦Arrhenius本构方程，并构建了不同应变条件下的热加工图，旨在为6061铝合金的热加工工艺制定和优化提供理论依据。

1 实验材料及方法

实验材料选择6061铝合金，其化学成分及质量分数如表1所示。选择φ8×12 mm的圆柱试样在Gleeble-3500热模拟试验机上开展等温热压缩实验，实验前在试样的端面增加二硫化钼和石墨薄片作为润滑介质，以降低试样与压头接触面之间的摩擦。根据6061铝合金材料的加工特性和企业提供的工艺参数范围，选择变形温度为350、400、450和500 ℃，应变速率为0.01 、0.1 、1 和10 s-1。实验前，将试样以2 ℃/s的加热速率加热至实验设定温度，保温4 min使试样组织均匀化，在应变速率为0.01 、0.1 、1 和10 s-1下进行压缩实验，最大压缩量为60 %，当实验结束后，立即对试样进行水淬，以保全高温变形组织。将压缩试样沿轴向切开，经打磨、机械抛光，采用HF 1.5 mL、H3PO430 mL和H2O 60 mL配比的腐蚀剂腐蚀约1 min，并在MV5000光学显微镜下观察金相组织。

表1 6061铝合金化学成分及质量分数

2 结果与分析

2.1 应力-应变曲线

6061铝合金在不同变形条件下的应力-应变曲线如图1所示。由图1可知，在相同变形温度条件下，流变应力随应变速率增加而增加，这是因为应变速率的增加，单位时间内的变形量和位错的数量也快速增加，造成大量位错相互缠结进而阻碍位错的运动，使得金属抗变形能力提高，因此，流变应力也增加[3]。在相同应变速率条件下，流变应力随变形温度升高而降低，这是因为材料的热激活能和原子内能随温度升高而增加，导致阻碍位错运动的阻力降低，使得金属抗变形能力减弱，有利于材料变形，流变应力降低[7]。

由图1(a)可知，除了变形温度为450、500 ℃外，6061铝合金发生明显的动态软化现象。流变应力在变形初期阶段增长速率快，这是由于材料内部的位错数量随变形量的增加而增加，导致大量位错缠结并阻碍位错运动，且在此阶段动态软化率低于加工硬化率，因此，流变应力增加。当流变应力到达峰值应力后，材料出现动态软化现象，这是因为随着变形量的增加，材料内部的变形储能也不断增加，为动态再结晶和回复的出现提供能量，使动态软化率高于加工硬化率，导致流变应力降低。随着变形量的增加，流变应力逐渐稳定，说明加工硬化率和动态软化率处于动态平衡状态。从图1(c)(d)可见，在应变量超过0.1后，除400 ℃外，流变应力缓慢增加，这是因为高应变速率下材料变形时间变短，动态回复进行不充分或者没有出现，导致不能完全克服加工硬化的影响。另外在高应变速率下大量位错出现缠结，严重阻碍位错的运动，从而增加流变应力。

图1 6061铝合金在不同应变速率条件下的应力应变曲线

2.2 Arrhenius本构方程

Arrhenius本构方程是用来描述材料在热变形过程中温度、应变速率与流变应力之间的关系，其表达式为[8]：

(1)

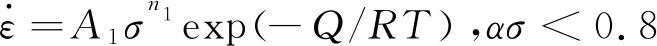
(2)

(3)

采用最小二乘法线性拟合求解Arrhenius本构方程中α、n、Q和A参数的值。对式(2)(3)两边分别取对数可得：

(4)

(5)

假设热变形激活能Q与温度无关，对式(1)两边同时取对数可得：

(6)

图2 Arrhenius本构方程参数求解

变换式(6)可得：

(7)

6061铝合金Arrhenius本构方程为：

exp(162.462/5.208RT)]

(8)

2.3 6061铝合金试样热压缩实验的数值模拟

在Deform软件材料库中重新定义6061铝合金材料的Arrhenius本构方程参数。选取6061铝合金试样在温度450 ℃、应变速率1 s-1以及应变量0.91的热压缩过程进行模拟分析。

试样在热压缩后其外形为腰鼓形，这是由于压头与试样端面存在摩擦力，导致试样沿径向变形，产生腰鼓现象，测量并计算实际实验和仿真分析试样最大腰鼓直径的平均值分别为12.933 和13.019 mm，误差为0.66 %；实际实验和仿真分析试样上端面直径平均值分别为11.86 和11.553 mm，误差为2.66 %；而试样下端面直径平均值分别为12 和11.582 mm，误差为3.61 %。

将图3(a)载荷-行程曲线通过式(9)和式(10)转换为应力-应变曲线，如图3(b)所示。

图3 实验与数值模拟结果对比

(9)

(10)

式中，l0为试样原始高度，mm；△l为试样压缩高度，mm；F为载荷，N；r为试样的原始半径，mm。

由图3可知，实验与仿真分析的载荷-行程曲线和应力-应变曲线的变化趋势基本一致。图3(a)中的载荷在行程为0.5 ～ 4 mm的区间偏差相比其他区域大，平均误差为6.54 %。这是因为实际压缩过程的摩擦系数是变化的，而数值模拟软件中设定的摩擦系数是定值，导致两者出现一定偏差，这也引起应力出现偏差，如图3(b)所示。应力在应变0.04 ～ 0.4的区间，数值模拟的应力值高于实验的应力值，两者的平均误差约3 %。这是由载荷和压缩高度两者的偏差共同引起的。因而，本文建立的Arrhenius本构方程能较好地描述6061铝合金材料的高温流变行为。

2.4 6061铝合金热加工图建立与分析

动态材料模型中材料吸收的能量主要以两种方式耗散：一是材料发生塑性变形所消耗的能量，用G表示；二是材料变形过程组织演变消耗的能量，用J表示[9]。

(11)

应变速率敏感指数m表达式如下：

(12)

Murty提出了任意类型的流变失稳准，则G的积分可以转化为[17]：

(13)

热变形过程中，材料微观组织演变所消耗能量的功率大小，可通过定义无量纲的能量耗散效率参数η表征。

(14)

理论上能量散耗率η越大，材料加工越容易，而在能量散耗率较高的情况下也可能出现失稳现象，因此，能量散耗率η不能完全体现材料加工的好坏。需要对热加工图进一步补充，Murty提出材料失稳的判据条件如式(15)。

2m/η-1<0

(15)

6061铝合金在不同应变下的热加工图如图4所示。图中数值表示能量散耗率，阴影部分表示流变失稳区域。由图4可知，当应变为0.2时，热加工图中没有出现能量散耗率峰值，但出现一条山脊，能量散耗率在31 %左右。当应变分别为0.4、0.6和0.8时，6061铝合金的热加工图有且仅有一个峰值，即变形温度460 ～ 500 ℃，应变速率0.1 ～ 0.5 s-1，其能量散耗率在33 % ～ 36 %之间，且峰值区域在应变为0.2时的山脊区域处。由图4可知，流变失稳区域主要集中在高应变速率区，且流变失稳区域随着应变增加而扩散。在变形温度较低时，可能产生热黏塑性失稳而形成绝热剪切，导致低温区域可加工范围较窄。而低温高应变速率下，由于材料内部因变形产生的热量在短时间内无法扩散至其他区域，温度分布不均匀，进一步影响该合金在发生塑性变形时微观组织分布，导致该区域的能量散耗率较低。因此，6061铝合金最佳工艺参数范围为：变形温度460 ～ 500 ℃，应变速率0.1 ～ 0.5 s-1。

图4 不同应变下的热加工图

试样在不同变形条件下压缩后的组织分别如图5所示。从图5可见，组织沿轴向被压扁，沿径向被拉长。图5(a)中晶粒组织细小且狭长，分布较为均匀，这是因为该变形条件下，材料的热激活能和驱动力低，难以满足动态再结晶出现的条件。由图5(b)(c)可知，组织沿轴向被压缩的程度减小，且分布越来越均匀，并出现细小的晶粒，表明在这两种变形条件下存在动态再结晶现象。从图5(d)可以看出，在该变形条件下组织分布不均匀，靠近试样中部的组织呈纤维状，且晶界变得模糊，靠近端部的组织粗大，且分布不均匀，这是因为靠近试样中部区域的变形量较大，而靠近端部的变形量小，且高应变速率下析出相聚集在被压扁的晶界附近，这将降低晶界的结合强度，导致材料内部产生裂纹，影响材料的力学性能[10]。结合热加工图可知，变形温度500 ℃，应变速率0.1 s-1时的能量散耗率高，且组织分布均匀，材料的力学性能最好。