基于氧化锌薄膜的可见光完美吸收体仿真研究

杨辉，熊娟，杨伟佳，杨焱，王钊

(湖北大学物理与电子科学学院,铁电压电材料与器件湖北省重点实验室,湖北 武汉430062)

0 引言

近年来，基于局域表面等离子体共振(LSPR)的等离子体超材料，由于其独特的电磁特性和广阔的应用前景而引起研究人员的广泛关注.基于等离子体纳米结构的光吸收体在太阳能电池[1]、超材料[2]、光电探测器[3]、传感器[4]、纳米成像器件[5]和热辐射器件[6]等方面展现出巨大的应用潜力.1952年，Salisbury等[7]首次提出将由一层金属基材、一层介电层和一层薄的顶部金属层组成的三明治结构作为雷达波完美吸收体的雏形概念.2008年，Landy等[5]首次证明了等离子体超材料理想吸收器后，该领域研究迅速发展.

传统的超材料吸收器(MMAs)通常由三明治型三层结构组成，包括顶部周期性金属层、中间介电间隔层和底部金属层.通过对结构参数的优化，使MMAs的阻抗与自由空间阻抗相匹配，使反射和传输同时最小化，可在一定频率下达到对特定波长电磁波的完美吸收.近年来，国内外学者利用先进的纳米制造技术设计并制造了基于纳米粒子[8]、纳米锥体[9]、纳米孔阵列[10]和纳米光栅[11]等一系列不同类型的增强吸收型纳米结构，研究了不同结构的形状、尺寸、材料以及介电环境等因素对GHz[5]、THz[12]、中红外[9]、近红外[11]和近光波[13]等一系列波段电磁波吸收特性的影响.然而，由于亚波长结构的制作限制，目前对可见光区范围内完美吸收体的研究较少.

本文中提出一种基于氧化锌薄膜三明治结构的一维光栅可见光完美吸收体.采用有限元仿真对所提出的完美吸收体结构进行建模与仿真，分别对其金属层的厚度、绝缘体的厚度、光栅层的厚度和宽度及完美吸收体结构的周期等进行研究，实现了在可见光波段的近完美吸收.

1 仿真设计

1.1 设定物理场采用COMSOL Multiphysics软件中的射频(RF)模块进行仿真研究.该模块下有传输线(tl)、电磁波时域显示(ewte)、电磁波瞬态(temw)、电磁波频域(emw)4种自定义应用模式.而在emw中有频域、特征频率、模式分析及边界模式分析等几种研究类型可供选择，并且频域研究类型可用单一或者多频率的源驱动仿真.本文中选择RF模块下的emw模式在可见光频段范围的研究.

1.2 建模与参数配置本文中设计的理想吸收体结构的如图1(a)所示.其中，于X、Y方向设置周期性边界条件，上、下端口分别设置“on”、“off”状态，入射光的偏振方向为X方向；ZnO的介电常数为8.3，金属层的波电方程选用Drude-Lorentz色散模型，且Au的等离子体频率设置为ωp=1.37×1016rad/s，时间衰减阻尼ω∞=12.24×1013rad/s；然后对其进行网格剖分，其中最小单元尺寸为2×10-8m，最大单元尺寸为1.6×10-7m.

1.3 计算和结果处理通过仿真计算器件S参数，根据S参数矩阵反演法计算反射谱曲线，如公式(1)所示：

R(ω)=|S11|

(1)

其中，S11为反射系数.此外，光吸收体的吸收度用公式(2)计算[14]：

A(ω)=1 -R(ω) -T(ω)

(2)

其中R(ω)、T(ω)分别是反射率、透射率.由于透射率为零，公式(2)可简单地表示为：

A(ω)=1 -R(ω)

(3)

利用以下公式计算光吸收体的有效输入阻抗Z[14]：

(4)

2 结果与讨论

众所周知，超材料吸收体的性能受到结构几何形状和结构尺寸的强烈影响.对图1(a)所示对光吸收体结构的各个参数进行电磁仿真.首先，我们研究不同厚度的介质层(ZnO)对设计结构反射光谱的影响，在仿真中，只改变氧化锌层的厚度，对其结构的反射光谱进行分析，如图1(b)所示，随着介质层(ZnO层)厚度的逐渐增加，共振波长将发生明显的红移.从图1(c)中可以看出，随着介质层(ZnO层)厚度从20 nm增加到70 nm时，总体上其光吸收体结构的反射率增大，这是由于ZnO层厚度增加使上层光栅层与底层Au膜之间的距离也相应增大，从而导致两层金属层之间的近场等离子体耦合变弱，反射率增加.

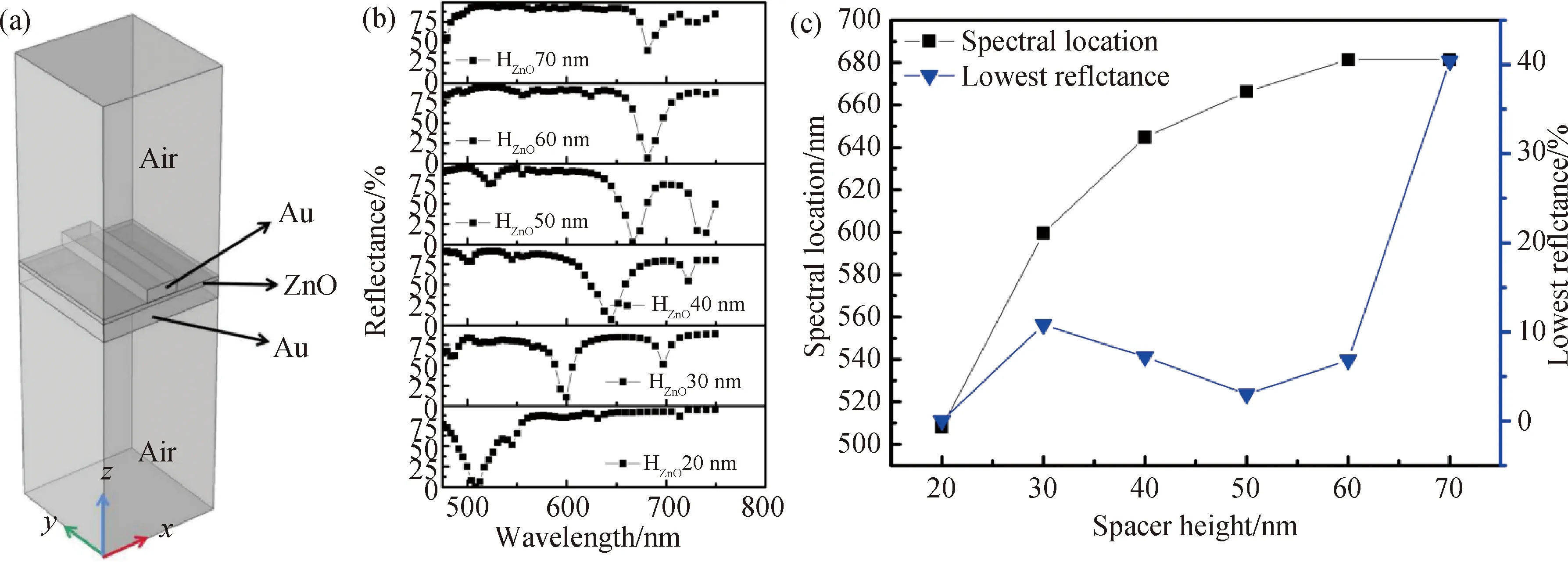
图1 (a)不基于ZnO薄膜的一维光栅可见光完美吸收体结构的单元几何模型；不同ZnO层厚度的(b)反射光谱图、 (c)共振波长和最低反射率图

图2为在COMSOL仿真中不同底层(金层)厚度对光吸收体结构反射率光谱的影响.从图2(a)中可以看出，随着不同底层(金层)厚度增加，其共振波长变化不大.此外，如图2(b)所示.当金层厚度在60 ～ 120 nm之间时，反射率可维持较低的值，而当金层厚度超过120 nm时，反射率明显增大，这是因为当达到一定厚度时，底层金属与上层光栅之间的耦合达到一定的饱和，金层厚度增加导致金的金属颗粒衍射大大增强，因此反射率快速增大.由于底部Au膜的作用有两方面，一方面是抑制光的透过作用，另一方面是由顶层光栅衍射进结构中的光照射到Au层会产生光生电流，此时只需要Au厚度大于Au的趋肤深度的2倍即可[4].基于此，金层的最佳厚度为80 nm.

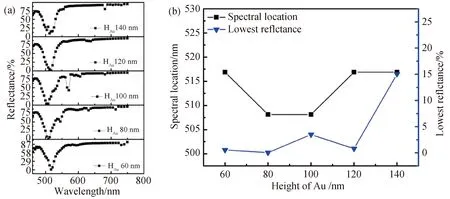
图2 不同金层厚度的(a)反射光谱图、 (b)共振波长和最低反射率图

图3给出在COMSOL仿真中不同金属光栅厚度对光吸收体结构反射率光谱的影响.图3(a)为不同金属光栅厚度的反射率光谱图，从图3(a)中可以看出，当金层厚度小于70 nm时，随着金层厚度的增加，共振波长会发生蓝移；随着金层厚度进一步的增大时，共振波长会发生红移.如图3(b)所示，随着金属光栅厚度的增加，反射率先减小后增大，最佳厚度为60 nm.随着金属光栅厚度的增加，反射率先减小后增大是由于增加厚度时会增大LSPR的激发，从而增大入射光的吸收率，反射率减小；而当厚度进一步增大时，由于厚度太厚会增加入射光的反射，而LSPR随着厚度的增大进入饱和，因此反射率增大[15].

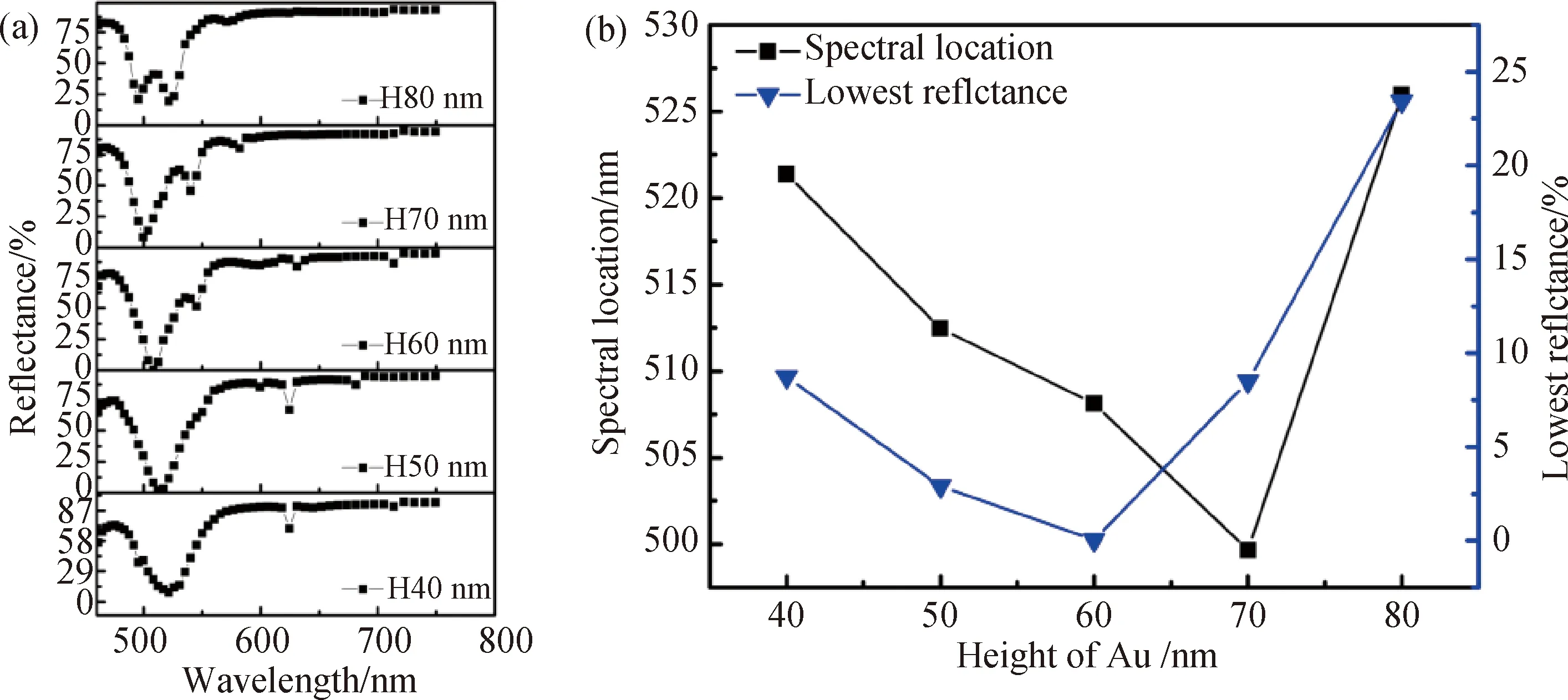
图3 不同光栅层厚度的(a)反射光谱图、(b)共振波长和最低反射率图

图4为在COMSOL仿真中不同周期对光吸收体结构反射率光谱的影响.我们研究光吸收体结构的周期在350 ～550 nm范围内的光吸收特性，仿真结果如图4(a)所示，随着光吸收体结构周期的增加，反射光谱共振波长向长波长方向移动，这是由于在增大结构周期而线宽不变的同时，光栅之间的宽度会变大并由此影响衍射效应，导致外部进入到光吸收体内部的光波长会向长波长方向移动.如图4(b)所示，反射率随着光吸收体结构周期的增加先减小后增大，这是由于固定光栅宽度下，结构周期的增大会使入射到结构中的光增加，从而增大入射光的吸收率，反射率减小；进一步增加结构的周期，光栅之间宽度进一步增大会导致LSPR的激发减弱，从而降低入射光的吸收效率.

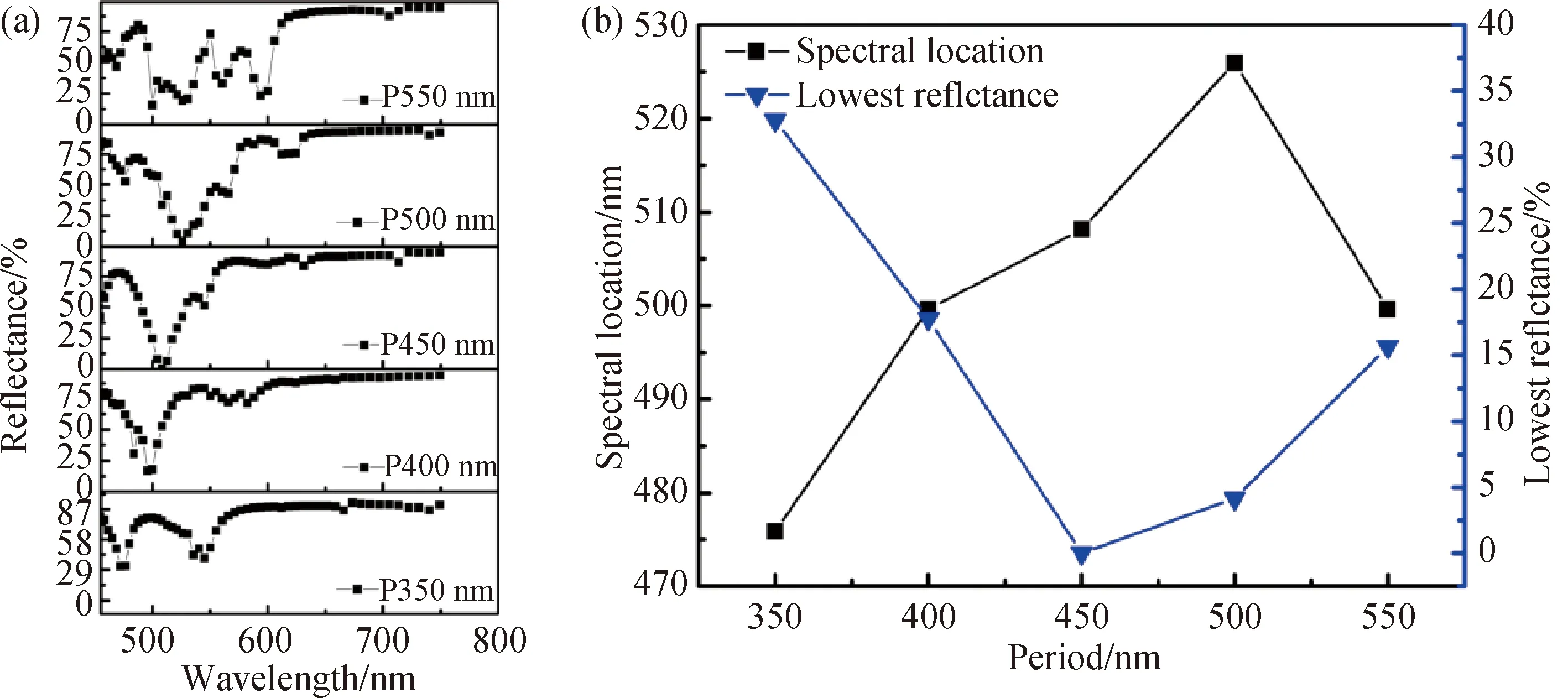
图4 不同周期的(a)反射光谱图、(b)共振波长和最低反射率图

图5为在COMSOL仿真中不同光栅宽度对光吸收体结构反射率光谱的影响.如图5(a)所示，当光栅宽度从80 nm变化到130 nm时，共振波长向短波长方向移动，这是由于周期不变，线宽逐渐增大的过程中，光栅之间的宽度逐渐变小，导致光的衍射波长变短，即一维光栅层选择可吸收波长逐渐变短.从图5(b)中可以得到，光栅宽度为100 nm时吸收最强，在光栅宽度低于100 nm时，结构的吸收强度较弱，这是由于LSPR的激发减弱导致上层金属和底层金属膜之间的等离子体耦合强度减弱造成的；在光栅宽度大于100 nm时，反射率可维持较低的值，随其宽度增大略增大，这主要是由于反射入射光的有效金属面积增加，导致其入射到结构中的光减少.

图5 不同光栅宽度的(a)反射光谱图、(b)共振波长和最低反射率图

通过对光吸收体结构的各个参数进行电磁模拟仿真，我们得到基于ZnO薄膜的光吸收体结构的最优参数，即周期P=450 nm，光栅宽度W=100 nm，上层金属(Au)厚度为60 nm、介质层(ZnO)厚度为20 nm、底层金属(Au)厚度为80 nm.图6(a)为优化参数条件下仿真得到的光吸收体的反射光谱和阻抗谱，从图6(a)中可以看出，该结构在508 nm处对光的吸收效率达到100%，且阻抗值为1，与真空阻抗相匹配，实现了对可见光的完美理想吸收.图6(b)、(c)分别为光吸收体在最优参数结构尺寸下共振波长550 nm处仿真得到的磁场和电场图.从图6(b)、(c)中可以发现光吸收体中的最大磁场分布在ZnO介质层且位于光栅的正下方，有很强的局域性，这是由金属光栅表面等离子体共振产生的电偶极子共振以及金属光栅与底层金属膜之间耦合的结果.因此，在共振波长处，两金属层之间的局域电磁场得到增强.这也很好地解释了特定波长的入射光经光栅衍射进入介质层，在一定条件下会在介质层被耦合从而完成能量转换，使入射光被吸收.从图6(c)中可以看出光吸收体中的电场主要分布在光栅的边缘处以及介质层中，这是因为相邻光栅之间产生的电荷也存在一定的电场耦合，进一步验证光栅宽度和结构周期变化仿真的结果；介质层中的电场分布是入射光在金属光栅表面产生的等离子体激发所形成的电场与磁场耦合共振的结果，当达到最强的电场和磁场时，完美吸收体在特定波长处表现出最佳的吸收特性.从电场和磁场仿真结果中可以得出，基于ZnO一维光栅的完美吸收体对可见光的完全吸收效应是由局域的磁和电耦合共振激发造成的，这种强烈的共振效应使完美吸收体获取光的能量，并在金属层内部损耗掉极少部分能量，从而在介质层中完成能量转换.

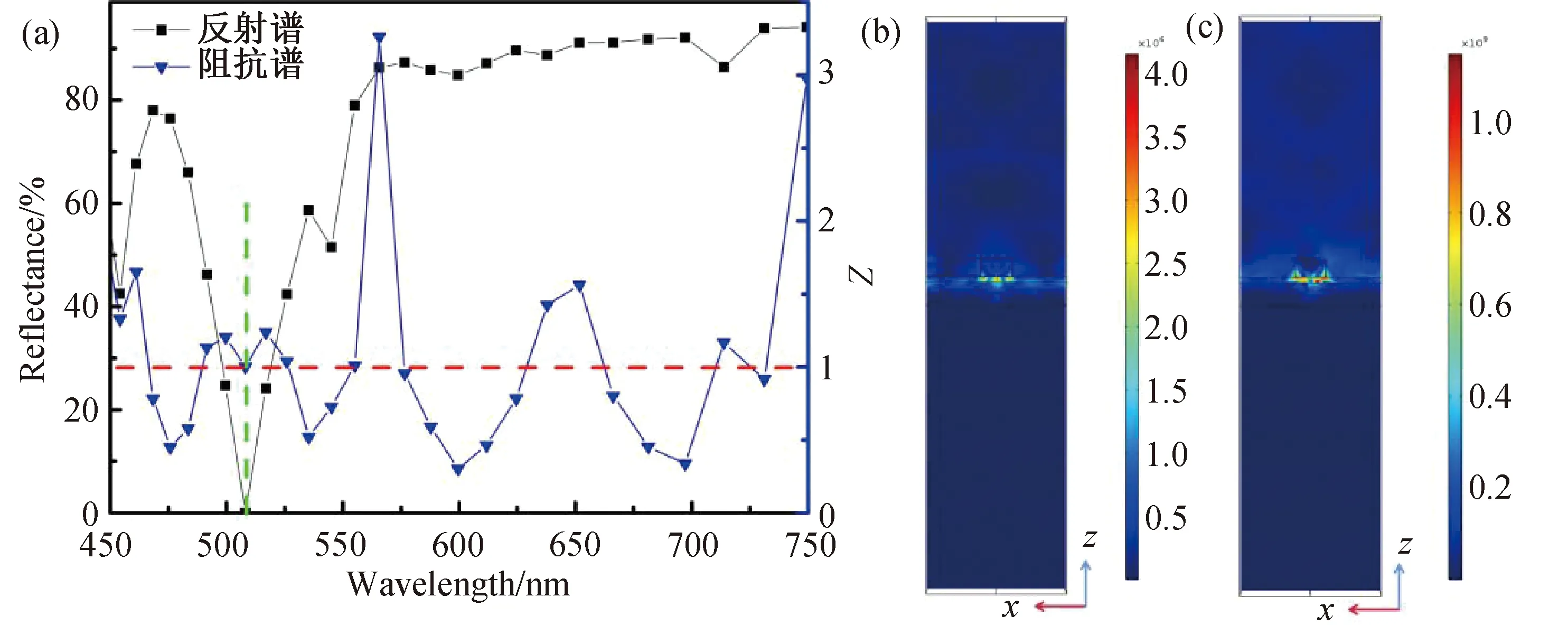
图6 最优参数光吸收体结构的(a)反射光谱和阻抗谱图、(b)磁场图和(c)电场图

3 结论

本文中提出一种基于氧化锌(ZnO)一维光栅的可见光范围的光学型完美吸收体(Au-ZnO-Au).采用COMSOL有限元方法对所提出的完美吸收体的结构参数与光学特性之间的关系进行模拟仿真，系统地研究Au、ZnO和光栅(Au)层的厚度以及完美吸收体结构的尺寸对光吸收特性的影响规律.结果表明，当其他层厚度保持不变时，增加ZnO厚度会使共振吸收峰发生红移；增加底层Au层厚到120 nm时，反射率可维持较低的值，而当金层厚度超过120 nm时，反射率明显增大；增加金属光栅层厚度会使反射率先减小后增大，在厚度为80 nm时反射率最小.此外，当完美吸收体结构的周期长度为350～550 nm范围时，结构对可见光具有良好的吸收特性，且共振吸收峰随周期长度的增加发生红移；改变光栅的宽度，也会对结构的光吸收特性产生显著影响.仿真结果表明，当完美吸收体结构的周期为450 nm、光栅宽度为100 nm、光栅层、ZnO层及底层金属(Au)的厚度分别为60、20、80 nm时，入射光的波长为508 nm处时完美吸收体的结构阻抗(ZStru)与真空阻抗(ZVac)实现了完美阻抗匹配且器件对可见光的最大光吸收率达100%.