Hankel滤波算法在可见光监控图像去噪中的应用
2022-03-16孙婷婷崔少华孔令坤董世稳黄金乐
孙婷婷,崔少华,孔令坤,王 勇,董世稳,黄金乐
(1.淮北职业技术学院计算机系,安徽 淮北 235000;2.淮北师范大学物理与电子信息学院,安徽 淮北 235000)
0 引言
视频监控一般采用可见光和红外两种技术采集,其中可见光技术采集的视频图像具有细节突出、边缘轮廓清晰等优点,但受制于采集时间和光亮度,红外技术可以在夜晚和光照度低的情况下采集视频图像,但是存在纹理模糊、分辨率低等缺点,综合考虑之下,可见光视频监控在现实生活中应用更多。由于采集环境的复杂性,可见光视频图像中往往包含大量噪声,为后续安防工作的开展带来很多困难,因此针对该图像进行去噪具有重要的研究意义。
传统的去噪方法有小波变换法、离散余弦变换、滤波法等,其中滤波法又包含空域滤波法和频域滤波法两大类。滤波算法的基本原理是在时域或者变换域内图像信息和噪声存在差异,采用合适的滤波器将二者分离从而达到去除噪声的目的。对于滤波法而言,选取合适的变换域和滤波系统是去噪的关键,郭慧娟等[1]采用MMM(Mixed-Median-Mean)算法将中值滤波和均值滤波相结合,在时域内(像素序列)以有效的像素替换原始含噪图像的像素。秦毅等[2]以Curvelet变换为基础,在变换域内设定合适的阈值滤除噪声值,通过重构得到去噪图像。孙婷婷等[3]在变换域内进行研究,以加权本征图像为分解因子,将含噪图像进行分解并选取合适的维度重构,以压制污染图像中的噪声。文献[2]和[3]的实验表明,相比传统时域去噪,变换域滤波去噪更容易被人为控制,效果更佳,然而实际工程所采集的噪声和图像信息并非完全孤立,上述文献在研究变换域去噪时,往往对各图像信息的相关性考虑欠缺,因此去噪的效果并非理想,还有较大提升空间。
为了改进上述研究成果的不足,提高去噪效果,以增强变换域内各图像信息之间的相关性为切入点,引入Hankel滤波算法,将含噪图像以Hankel矩阵排列,提高污染严重区域的各点信息的相关性,在变换域内使得图像信息和噪声的差异越来越明显,更利于噪声的滤除,从而使重构后图像去噪效果更佳。不同噪声强度下的实验表明,该方法能切实去除污染图像中的噪声,提高传统SVD算法去噪的效果。
1 变换域内去噪原理
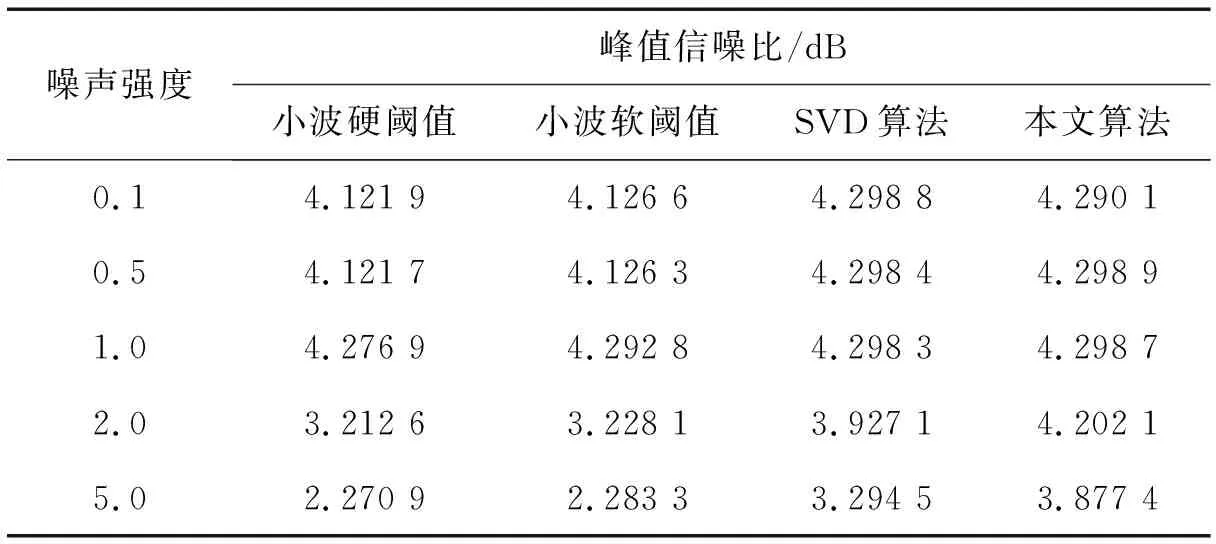
若有一个灰度图像其二维数组定义为S,大小为m×n(通常m Xm×n=Sm×n+Nm×n. (1) 若有一维信号c=(c1,c2,…,cm),将其排列成为Hankel矩阵的形式[4]: (2) 将H定义为一个Hankel矩阵,它的每条反对角线上的元素相同,若连接第一行和最后一列元素,其连接项就是原始信号c[4],将矩阵扩展为 (3) 假设,ci=si+ni,i=1,2,…,m,其中,si为有效信号,ni为噪声(随机信号),那么H又可以定义为 (4) 式(4)中H表示含噪信号(原始信号和噪声信号混合),以高斯随机噪声为例,虽然理想随机噪声各点之间是统计独立的,但是原始有效信号各点之间存在相关性,进过Hankel矩阵的排列,在一定程度上增强了其相关性,有利于后续的分解与重构。对矩阵H进行奇异值分解: (5) 假设有二维灰度图像(含噪)的大小为m×n,首先取出第一行图像信息排列成式(2)的Hankel矩阵,将排列的Hankel矩阵进行奇异值分解,根据奇异值分布图选取p阶重构恢复该行图像数据,此时图像中的随机噪声已经被压制了,但是一般情况下重构后数据已经不是Hankel矩阵了,需要将其反对角线上的元素进行平均,得到真实值的近似值构成的Hankel矩阵。再取出下一行图像信息,重复上述操作,直到对所有行的图像数据进行了噪声衰减。具体处理流程如图1所示。 图1 Hankel算法对图像去噪的流程 以室外监控提供的可见光图像为研究对象,在噪声污染的情况下分别对其进行小波滤波、SVD滤波和Hankel算法去噪。如图2(a)所示,原始监控图像来源于俄亥俄州立大学提供的OTCBVS Benchmark Dataset(T Dataset OSU Color-Thermal Databas)数据库,图2(a)监控图像中包含建筑物、树枝、车辆和行人,这对去噪时恢复的特征细节提出了更高的要求。由于Hankel算法去噪针对的二维图像,因此图2(a)为处理后二维图像(原图为彩色图像),在图2(a)中加入强度为0.1的高斯噪声构成含噪图像(污染图像),采用小波滤波、SVD滤波和Hankel算法去噪后结果如图2(c)至(f)所示。 (a)原始图像 (b)加入高斯噪声结果 (c)SVD去噪结果图1 Hankel算法对图像去噪的流程 (d)小波硬阈值去噪结果 (e)小波软阈值去噪结果 (f)本文算法去噪结果图2 各算法对图像去噪结果 图2显示三种算法均能达到一定的去噪效果,其中,SVD算法依赖与奇异值分解结果确定重构空间,根据分解奇异值的差异,本实验选取前50个奇异值重构图像,由图2(c)可知,该算法去噪后图像存在较多的信息损失,去除噪声的同时对图像本身具有较大伤害,造成这种结果的原因在于SVD算法去噪仅依靠舍弃奇异值来实现,但是舍弃的奇异值中仍然包含有图像信息,要想去除更多噪声,则相应舍弃的奇异值越多,对应舍弃的图像信息也越多,该方法以牺牲图像有效信息换取去噪效果,耗损较大。相比SVD算法,小波算法去噪能力较差,其中软阈值比硬阈值去除的噪声更多(对比图2(e)与(d)),处理后的边缘信息较模糊,原因在于由于软阈值分解重构时,从小波分解后的小波系数中进一步舍去了部分小波系数,去除噪声的同时也损伤了较多有效信息。这些正是传统滤波算法的弊端。由图2(f)可知,本文算法在处理二维污染(噪声)图像时切实可行,具有更好的去噪效果,去除多余噪声的同时也保留了更多的图像信息(对比图2(c)与(f)的矩形框),究其原因是Hankel矩阵依赖各行(各点)信息之间的相关性,每处理一次数据后,为了在去噪后数据中去除更多噪声点,均采用原始图像真实值的近似值构成新的Hankel矩阵从而恢复原始图像,由于该算法注重原始图像数据的近似值,因此相比传统SVD算法,能去除更多噪声并对图像损伤更小。 为了增加实验样本的丰富性,分别在不同强度的高斯噪声下进行实验,通过峰值信噪比来量化衡量,实验结果如表1所示。设峰值信噪比为P,其定义为 (6) 一般地,P值越大表示yo与y越接近,逆变换从含噪图像中恢复原始图像的效果越好。由表1可知,本文算法P的值均高于其他算法,这表明本算算法的高效性,其中在小噪声时(表1中噪声强度于0.1~1.0时),本文算法对去噪效果的改善性作用不明显(各算法P值差异较小)。在大噪声时(表1中噪声强度于2.0~5.0时),本文算法的P值较其余算法增强较大。在噪声强度为5.0时,相比常用的SVD算法,本文算法提高了约0.6 dB的信噪比,有效改善了传统SVD算法的去噪效果。 表1 不同算法去噪后的峰值信噪比 在监控图像去噪处理中,由于滤波法具有易于实现的特点,并且算法结构简单,能有效地达到去噪效果,一直是广大学者研究的基础。针对传统变换域内滤波算法弱化图像各点之间的相关性问题,本文采用Hankel矩阵算法,在传统SVD算法的基础上可得更高效的去噪效果。然而,从图2实验结果和表1来看,本文算法仍然存在去噪不彻底、损失较多原始图像信息等缺点,这正是滤波算法的短板。因此,未来的工作将重点研究人工智能技术在监控图像去噪中的应用。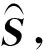
2 Hankel滤波原理
2.1 Hankel矩阵
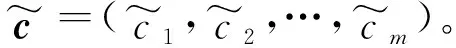
2.2 Hankel矩阵处理监控图像

3 实验结果



4 结语
