面向不平衡工业大数据集的SVM-tree分类算法研究
2022-03-16林君萍
林君萍
(福建船政交通职业学院,福建 福州 350007)
0 引言
伴随大数据时代的到来,工业大数据集呈现出海量性[1]、多源异构性[2]和不平衡[3]等特征。数据的不平衡性表现为数据集中一类样本的数量远多于另一类样本的数量,给数据的预处理、分类、特征提取和数据挖掘带来更大的难度[4]。以故障大数据分类和特征提取为例,如果少数类的故障数据样本仅占1%或更低,少数类样本容易被多数类样本所忽略,但少数类样本中往往也包含关键的和有价值的特征信息,由于数据集中多数数据样本和少数数据样本的比例失调,增加了数据误分类和特征提取错误的风险[5]。针对于不平衡工业故障大数据的分类问题,张玉征等[6]提出一种截断梯度特征法,通过对不同类别故障数据的梯度特征提取和分类,判断故障数据的不平衡率并提出少数样本的故障特征;曹鹏等[7]提出基于数据优化与指标评价的算法,预测少数样本的比例、重要性并识别出少数样的核心特征。现有算法能够从一定程度上优化不同类别数据之间的比例,提升数据分类的准确性,但在实际操作中难度较大,例如梯度的确定和评价指标的选取依赖于多种因素,且具有一定的主观性,当不平衡率过高时数据分类的准确率会随之降低,给特征提取和识别造成更大的难度。徐毅等[8]提出基于深度置信网络的数据训练模型,当数据维度较低时不平衡数据分类准确率尚且能够得到保证,但随着输入模型的非线性数据维数的提高,数据训练中易引起过拟合进而降低分类精度。为提升对不平衡大数据的分类精度,本文在借助K-means分类的基础上,构建了SVM-tree模型,并通过数据中心聚类和最优超平面分类的方式,选取相关性更优的数据样本,并以此改善数据集的不平衡性,提升数据分类性能。
1 不平衡数据集的噪声过滤与预处理
导致工业故障数据集中不同类别数据不平衡的原因,是存在数据小的划分或数据不相交的情况,例如,数据集中如果有含噪数据[9],那么有用数据就容易被湮没在噪声环境之中。不平衡率(Imbalance Rate)[10-11]是衡量大数据集不平衡程度的指标(假定故障集中只有两种数据),记为IR。
(1)
其中,N1max为第一类数据的最大值,N2min为第二类数据的最小值,且满足N=N1+N2,N是数据集中总体数据量。
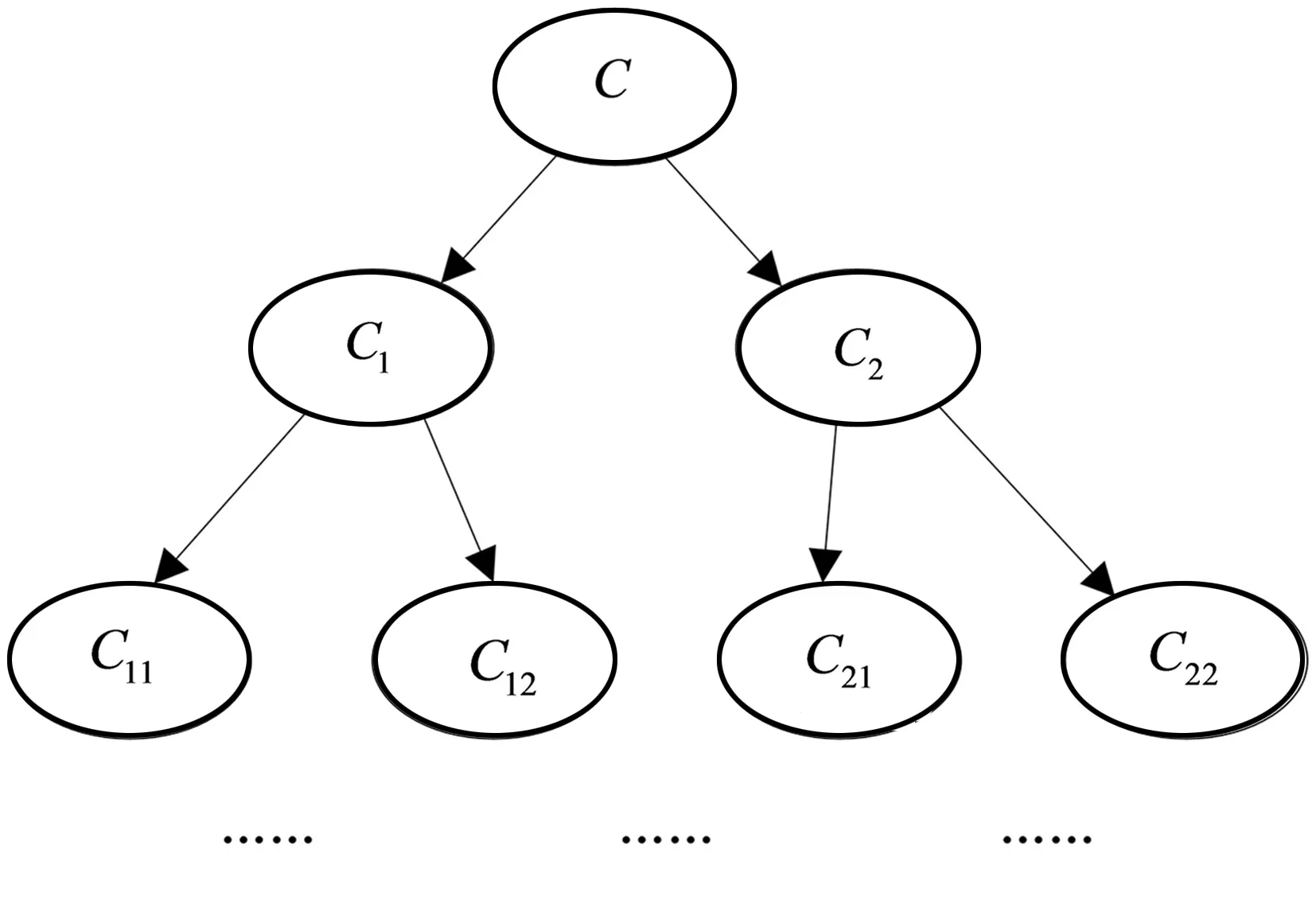
工业大数据通常利用布置在机器周围的传感器采集获取,来自环境的噪声和系统的噪声,会进一步加剧少数样本的稀缺性[12],因此滤除噪声干扰是不平衡数据集分类处理和特征提取的重要步骤之一。本文选择Tomek-links算法清除原始样本中的噪声,原始工业故障数据样本集中的两个不同类别的样本点,分别表示为ai和bj,样本点之间的欧式距离描述为d(ai,bi),如果不存在第三个样本点ak或bq,满足条件d(ai,ak) Step1 在采集的数据集中标定已知样本和待测样本,其中待测样本中含有噪声源。 Step2 计算全部待测样本和标定样本之间的欧式距离,并基于距离的远近做升序排列。 Step3 基于KNN算法的规则从待测样本选定K个样本,并利用多数投票规则确定待测样本的类别和属性。 Step4 需要考虑不同类别数据属性对样本类别的影响[13-14],引入数据属性的权重系数ωi,并计算与第三个样本点之间的距离(以样本点xk为例进行说明)。 (2) 加权计算之后再比较d(ai,ak)和d(ai,bj)之间值的大小,以判断样本点ak是否为噪声数据样本点。受KNN算法优化的影响,K值为噪声滤除算法的重要参数,K值的选定要与输入数据集的规模和不平衡率相匹配。如果K值过高,则会降低算法的噪声滤除性能;如果K值过低,则会提升真实样本的误判率。 在处理不平衡数据集时,需要重点关注数据集的非线性特征[15]和数据维数[16],支持向量机(Support Vector Machine,SVM)在解决数据高维问题上具有较明显的优势。由于SVM模型能够将数据从低维映射到高维,可解释性更强,且对数据的差距较为敏感,适用于解决高维不平衡数据集的分类问题。 利用SVM模型将去噪后的样本映射到高维空间,先要将故障数据样本集划分为训练集和测试集,其中训练集的任务是训练分类模型并确定模型的参数,测试集主要用于对不平衡数据样本的的分类。SVM分类器无论是用于数据训练,还是数据分类,都需要对目标样本做初始化处理,降低不平衡数据集分类的复杂程度,并提高不平衡数据分类的效率。本文选用K均值聚类算法(K-means clustering algorithm)进行迭代求解,设去噪后的不平衡数据集为Z,数据集中包含了n个有效样本对象,即Z={z1,z2,…,zi,…,zn},每个样本都包含了p维属性,满足条件zi∈Rp。K-means聚类指按照样本的特征将n个样本划分成m个簇,每个簇的簇心为ck,k=1,2,…,m,K-means算法在分簇时仍然基于欧式距离法确定样本之间的相似性程度,为避免在计算中出现负值,以样本对象到簇心之间的距离平方和作为目标函数E(ck)。 (3) 簇心通常为样本集中处于最优位置的数据样本,目标函数E(ck)值的大小对应样本到簇心距离值的大小,按照距离从小到大将全部样本条件到距离最近的簇排序。受噪声数据和新采集数据的影响,不平衡数据集的规模处于动态变化之中,因此数据分簇过程和簇心的选择都会发生变化。当需要重新选择新的簇心和计算样本到簇心的目标函数值时,重复执行上述步骤直到满足终止迭代的条件为止。 基于K-means算法进行样本聚类后,极大地降低了SVM分类的复杂度,使SVM分类器具备了处理大规模故障数据集的能力。SVM分类器从三维视角利用超平面解决二分类问题。将不平衡数据集中的每一个样本点都用一个二维坐标表示: Z={(x1,y1),(x2,y2),…,(xk,yk),…,(xn,yn)}. (4) (5) yk(ωTxk+h)≥1. (6) SVM分类器模型需要借助核函数将低维数据映射到高维,并达到数据分类的目的。能成为核函数的条件是,其矩阵必须满足对称性的半正定矩阵条件,本文选用高斯函数G作为SVM分类器的核函数: 其中,ζ是高斯核函数的带宽,当数据集的不平衡率值较大时,如数量多的样本与数量少的样本比值超过10 000,SVM的模型分类准确率会出现严重的衰减。 为提高模型在高不平衡率模式下的分类准确率,本文对经典的SVM分类器进行优化,构建SVM-tree模型。基于K-means聚类算法根据不平衡数据集的样本特征将样本集划分为m个簇,SVM-tree算法模型的数据训练以簇为单位展开,簇心的集合也就是训练集中心点的集合为C={c1,c2,…,cj,…,cm},按照簇数量的多少和规模的大小,将C分为若干子类,为了算法简便本文假定将C分为两个子类C1和C2,X1和X2是与子类C1和C2对应的训练子集。划分多个子集以后即使不平衡率再高,例如超过了10 000,仍旧可以在X1和X2之间建立一个超平面,SVM-tree分类器树型结构设计见图1。 图1 SVM-tree分类器树型结构 将C分为两个子类C1和C2,每个子类再向下细分,根据数据集的规模和不平衡数据集的比例划分为若干个层次,子类划分得越细,SVM分类器的数据处理能力越强。在树型结构构建过程中,以簇心集合C作为SVM-tree模型的根节点,两个子类C1和C2作为第二层节点,节点可以继续向上细化,树状模型的复杂度越高,节点子集的细化程度就越高。当SVM-tree的叶节点不可再分,仅包含一个类别时,叶节点对应的标签就是其所含类别的标签。在进行样本测试训练时,由于样本的不平衡性会提升故障数据测试与分类的难度,此时从根节点出发,利用SVM分类器的超平面判断对全部数据分类,并判定下一层次子节点的归属问题。经过多次的迭代和细化,直到叶节点不可再分就可以得到分类问题的最终结果。SVM-tree分类器训练完成以后,基于临时样本测试集检测分类器的数据分类效果,如果能够满足相关额测试要求,则停止计算完成迭代;如果仍未达到不平衡数据集的检测要求,则继续细化分类器的结构,提升分类器的数据分类与检测性能。 为保证实验的可变性和可靠性,本文全部实验均在相同环境下进行,其中硬件参数的选择和软件工具的选择分别见表1和表2。 表1 实验硬件环境 表2 实验用到软件工具与版本 实验用的数据集来自于UCI和KEEL的8组公开数据,以体现出模型的泛化性能和适用性能,数据集的相关信息见表3。 表3 实验数据集描述 SVM-tree不平衡大数据算法模型的构建以K-means数据聚类为研究基础。本文首先检验SVM-tree算法的数据聚类性能,数据聚类的误差值越小,表明算法的稳定性越强。以样本数据集中的Pblock和Letter为例(这两个数据集的规模较大,数据聚类的难度更大),分析SVM-tree算法的聚类误差变化波动情况,借助Matlab工具软件得到的统计仿真结果,见图2和图3。 图2 Pblock数据集聚类结果仿真 图3 Letter数据集聚类结果仿真 仿真结果显示,SVM-tree算法对Pblock数据集和Letter数据集的聚类误差值,均保持在较低的水平。在相同的实验参数和实验环境下,基于文献[6]、文献[7]和文献[8]三种传统算法和本文提出的SVM-tree算法,分别计算各分类算法针对不平衡数据集的分类准确率值,数值统计结果见图4至图6。 图4 文献[6]算法下不平衡数据集分类准确率统计 图5 文献[7]算法下不平衡数据集分类准确率统计 在三种传统不平衡数据算法下,不平衡率较低的数据集如Pima、haberman等,均能保持较高的数据分类准确率;而当工业大数据集的不平衡率较高时,如Flare、Yeast、Letter等,其数据分类准确率出现了较为明显的降低。尤其是不平衡率高且数据集规模大,算法分类性能的衰减较为明显。而本文提出的SVM-tree算法模型,就是要改善大规模数据集和高不平衡率条件下的数据分类性能。由于SVM-tree树状模型的层次和复杂结构可调,因此模式的适应性较强,在不平衡数据分类过程中成本代价也能够得到较好的控制,针对8个数据集的分类准确性统计见图7。 图7 本文算法下不平衡数据集分类准确率统计 实验数据统计结果显示,针对于Flare、Yeast、Letter等不平衡率较高的工业大数据集,SVM-tree树状模型和分类算法,依然能够获得较高的分类准确率。算法的运行效率也是评价不平衡大数据分类算法的重要指标之一,最后对比验证不同算法的数据分类运行时间,数据统计结果见表4。 表4 各分类算法的运行时间对比 统计数据结果显示,SVM-tree分类算法在大规模数据集和不平衡率较高的数据集分类时的优势更加明显,运行时间更短,算法运行效率相对于三种传统分类算法优明显的提升和改善。 工业大数据集具有不平衡性特征,如果不平衡率过高会直接影响数据分类的准确性。本文在经典SVM算法的基础上,利用K-means算法和子类划分方式,对经典SVM算法进行优化,并构建了SVM-tree分类算法模型,提升了模型对不平衡率较高数据集数据处理能力。实验结果表明,SVM-tree算法在数据聚类性能、不平衡数据集分类性能以及数据处理运行时间上具有优势。2 基于SVM-tree的不平衡数据集分类算法
2.1 K-means聚类
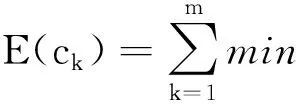
2.2 SVM-tree模型构建与不平衡数据分类的实现
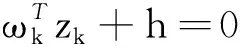
3 实验结果与分析
3.1 实验环境与数据集的选择

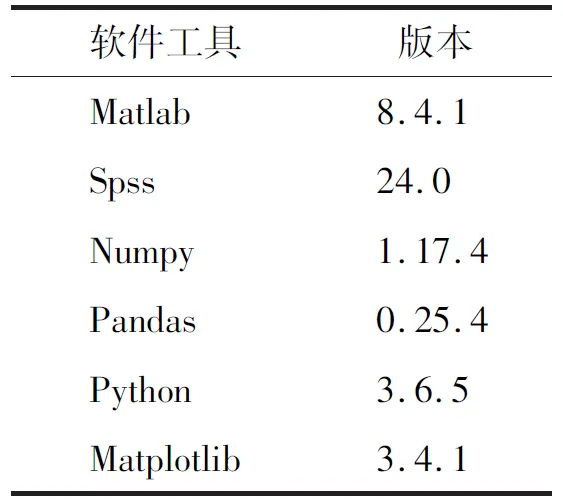
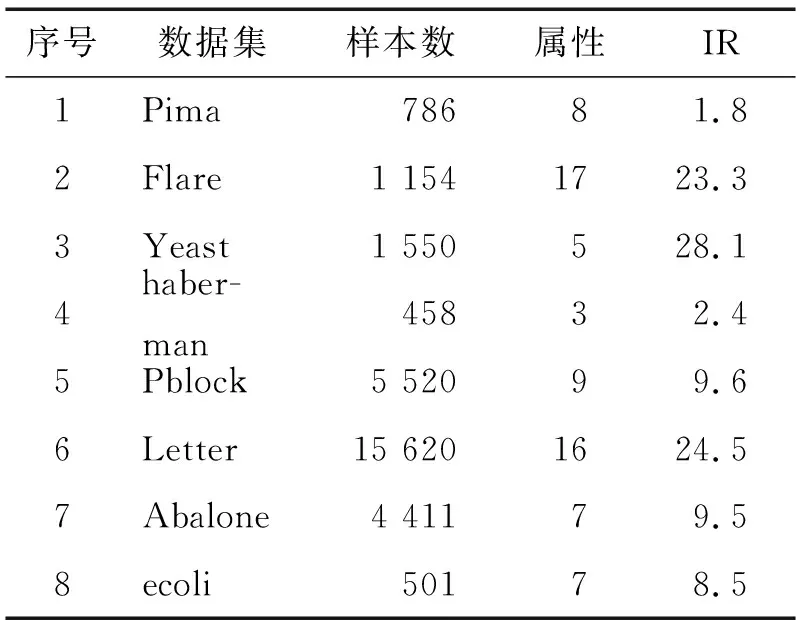
3.2 实验结果与分析
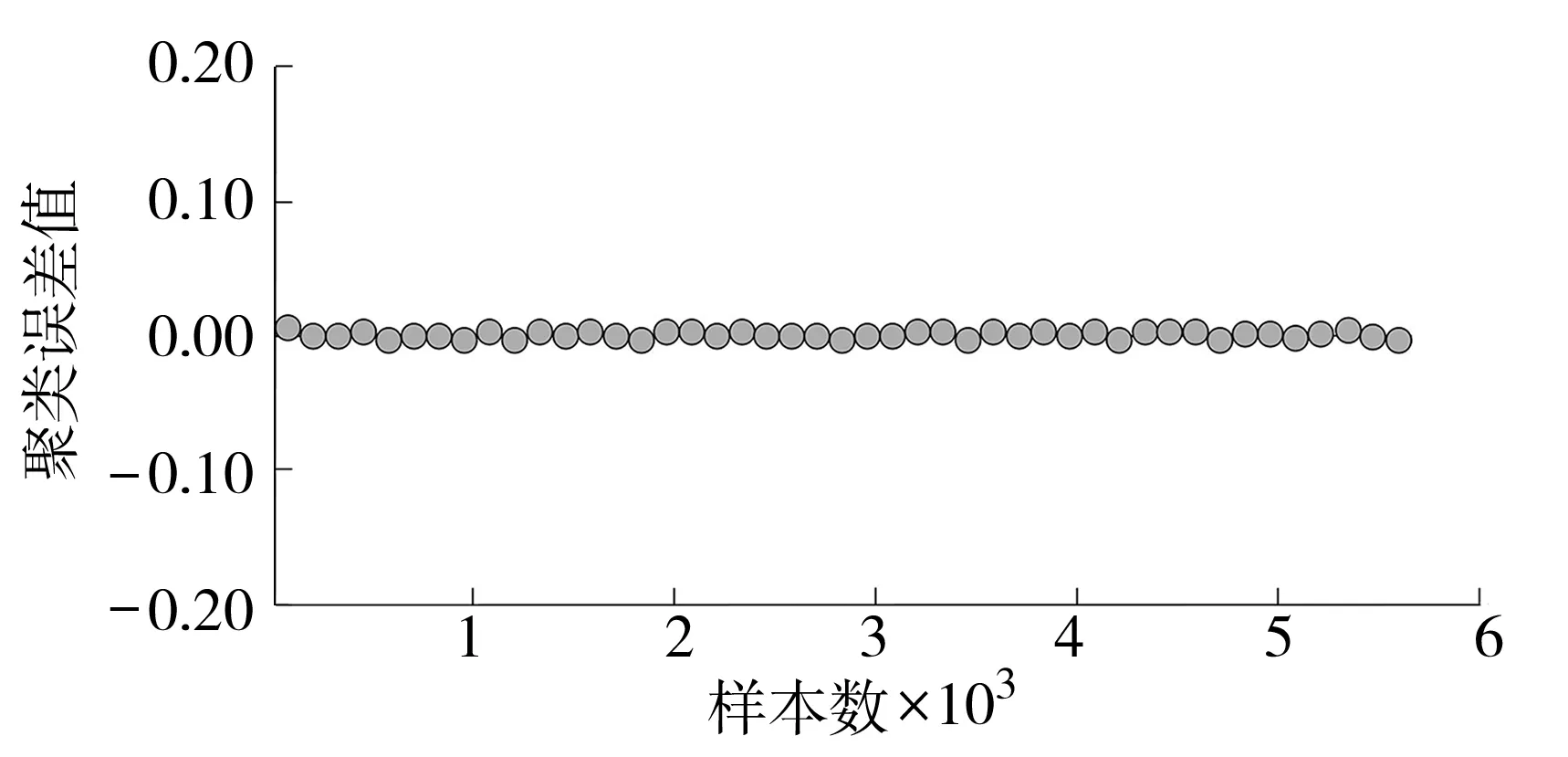
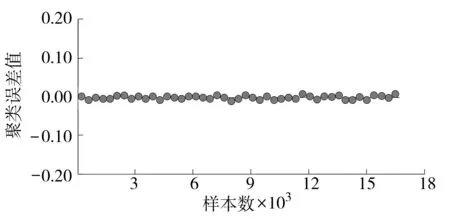
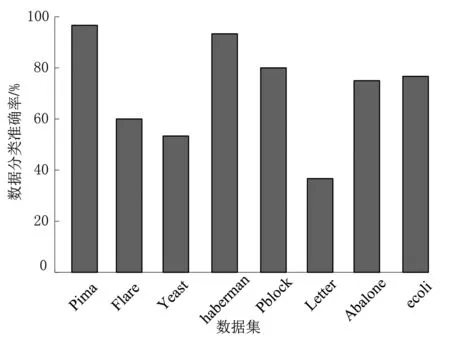
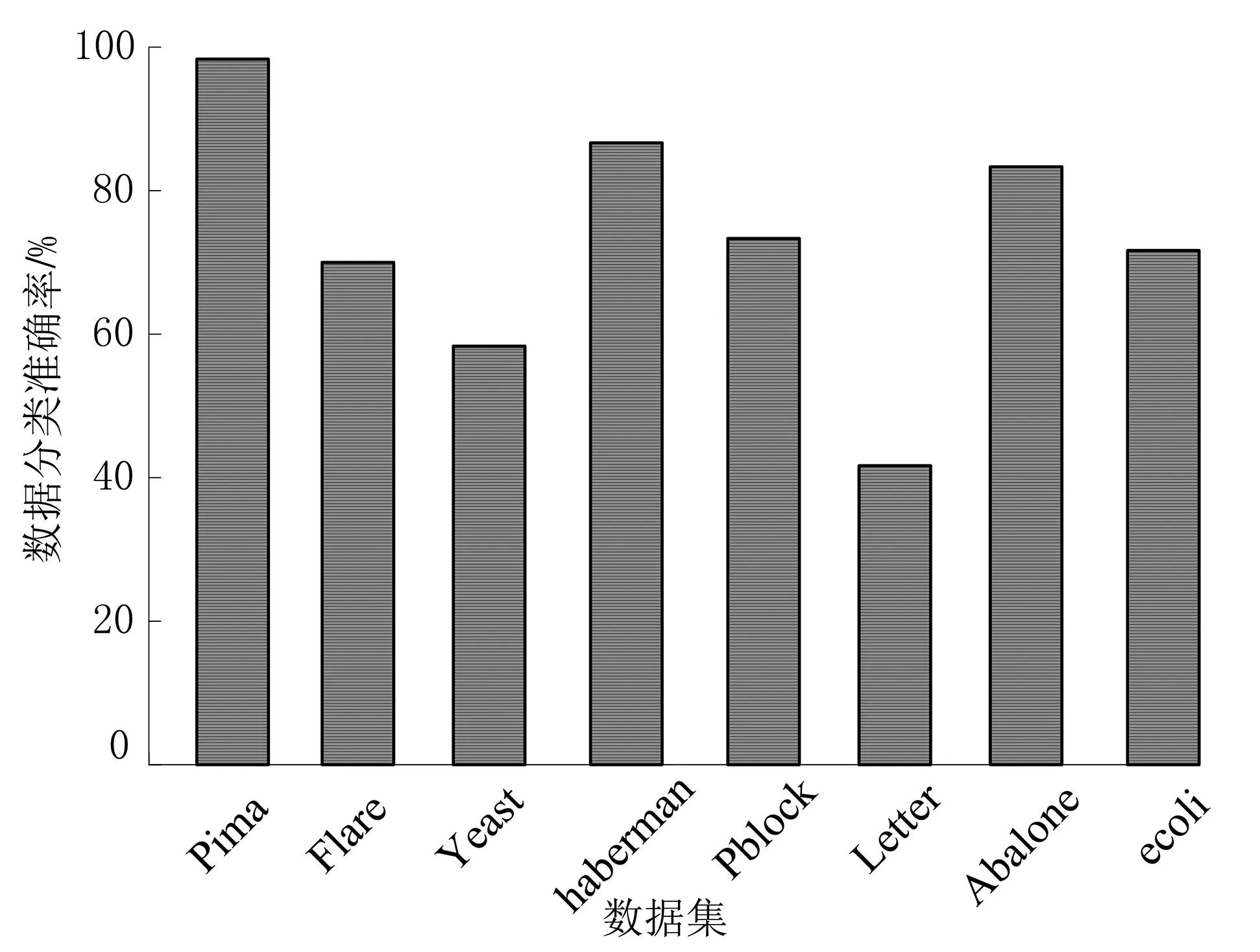
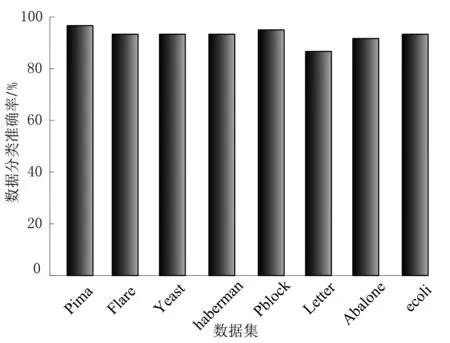
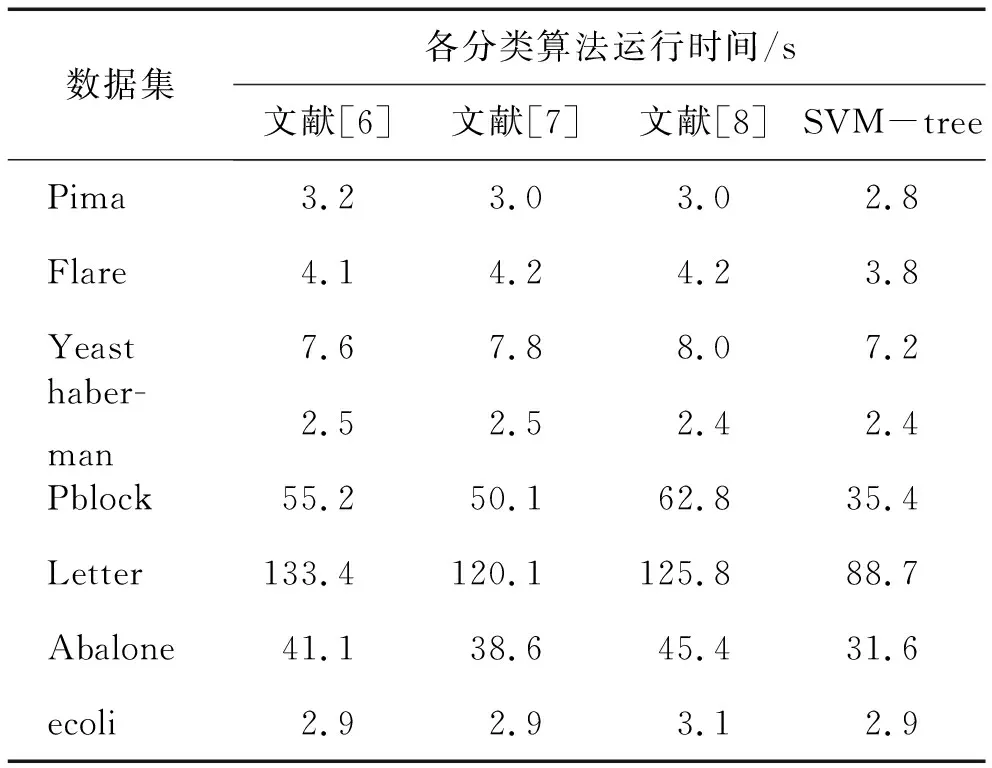
4 结语
