考虑季节特性的多时间尺度电动汽车负荷预测模型

牛牧童，廖 凯，杨健维，向悦萍

考虑季节特性的多时间尺度电动汽车负荷预测模型

牛牧童，廖 凯，杨健维，向悦萍

(西南交通大学电气工程学院，四川 成都 611756)

当前对电动汽车(Electric Vehicle, EV)充电负荷预测的研究大多集中在短期单一时间尺度，且鲜有考虑在较长时间尺度下不同季节电动汽车充电负荷存在的差异。基于此，提出一种考虑季节特性的多时间尺度电动汽车负荷预测模型。首先，考虑季节特性对EV的电池最大载电量、里程耗电量和空调耗电量的影响，结合时空分布规律建立短期日内的电动汽车充电负荷预测模型。其次，为了展现从短期(短时间尺度)到中长期(长时间尺度)的多时间尺度特性，建立考虑多种因素影响的Bass修正模型预测未来不同年份的EV保有量。结合短期EV充电负荷预测模型，可延展至中长期EV充电负荷的预测，从而实现综合短期、中长期的多时间尺度EV负荷预测。最后，采用上海市气温信息及行车数据进行仿真验证。结果表明，所提模型可以有效地预测未来数年EV发展趋势以及考虑季节特性的多时间尺度EV充电负荷。

电动汽车；负荷预测；Bass模型；多时间尺度；季节特性

0 引言

以电动汽车(Electric Vehicle, EV)为代表的新能源动力交通工具是解决化石能源危机与环境污染问题的重要措施之一[1-2]。近年来，EV在技术、政策、观念和市场的多方面推动下迅猛发展，截至2020年，其保有量在全球已逾900万辆[3]。一方面，充电桩的规划建设需紧跟EV保有量的增长；另一方面，大规模EV无序充电负荷与电网基础负荷叠加，将会引发诸如负荷峰谷差加大、运行约束越限、电能质量下降等问题[4-6]，影响电力系统的稳定性与经济性。为此，需要对EV保有量发展演化及充电负荷需求进行预测，从而为区域的充电设施及配电网设备的改造与新建提供合理参考和建议。

针对EV充电负荷预测，目前国内外已经做了大量研究，主要集中在对EV短期充电负荷预测的研究：充电概率建模[7]和时空分布建模[8-10]。在充电概率建模方面，文献[7]提出了基于不同类型电动汽车不同充电行为概率模型与蒙特卡洛模拟的电动汽车充电负荷预测方法。在时空分布建模方面，停车生成率模型[8]、时空活动[9]与出行链模型[10]、马尔可夫决策过程[11-12]等是电动汽车充电负荷预测研究中的常用模型。此外，还有许多研究从交通系统和电网系统相互耦合影响出发建立了电动汽车充电需求预测模型。文献[13]提出了交通路网约束下，模拟用户出行行为的电动汽车充电负荷时空预测模型。文献[14]通过建立交通网-配电网的交互模型预测典型区域路网充电负荷。文献[15]在路网与电网交互影响的基础上考虑车主主观心理非完全理性选择特性，提出了一种考虑路网-电网信息交互和用户心理的电动汽车充电负荷预测方法。除了上述模型驱动型预测外，随着大数据的发展，以实测数据分析EV充电负荷的数据驱动型预测手段也逐渐成熟。文献[16]中以深圳市出租车原始行驶数据提取居民出行规律，结合OD矩阵分析方法预测城市功能区充电负荷趋势。文献[17]通过对“滴滴”出行原始数据集进行大数据手段处理得到的出行特征数据，结合单体电动汽车模型建立电动汽车充电需求负荷模型。但上述预测方法得到的结果往往是在日内的短期充电负荷演变，无法推断较长时间后EV充电负荷变化趋势，并不能对EV充电设施与电网在未来建设规划上给予有效参考。

较长时间尺度下EV充电负荷预测研究相对较少，文献[18]为了研究EV发展趋势与负荷的交互影响，提出了一种保有量预测与车辆行为仿真交替进行的城市电动私家车中长期充电负荷预测方法。但其模型中忽略了车主出行目的的固定性，也并未考虑较长时间下季节特性对EV充电负荷的影响。

综上，现有的EV充电负荷预测研究大多着眼于描述单一时间尺度内尤其是短期可能出现的负荷特性，且忽略了季节不同所产生的充电负荷的差异，无法在多时间尺度下展现EV的发展变化趋势与充电负荷时空分布的演变。

基于此，本文提出一种考虑季节特性的EV多时间尺度充电负荷预测模型。首先，以出行链描述车辆的出行行为模拟车辆时空分布规律，再通过对EV电池最大载电量、出行耗电量的建模刻画季节特性对EV充电负荷的影响，建立短期EV充电负荷预测模型。其次，考虑传统能源汽车竞争、城市GDP发展、政策与油价等多种因素的影响，建立Bass修正模型，预测未来不同年份的EV保有量，更新短期EV充电负荷模型中的保有量，实现多时间尺度负荷预测。最后，通过算例仿真验证所提出的考虑季节特性的多时间尺度电动汽车负荷预测模型的有效性。

1 考虑季节特性的短期EV充电负荷预测

本节考虑不同季节特性对充电负荷的影响，建立EV短期负荷预测模型。首先，建立EV用户出行链，模拟EV用户出行行程。然后，考虑季节温度的影响，计算EV电池最大载电量0及出行耗电量1，由式(1)可获得行程后的剩余电量soc。最后，通过充电策略进行充电选择，充电完成后进行下一次行程，直到EV用户一天行程结束。

式中，1由行程的里程耗电量1_1以及空调耗电量1_2组成，如式(2)所示。

1.1 EV用户出行链

出行链是将EV用户不同的出行目的以特定的时间顺序链接起来，表示为各类出行活动构成的序列，可以很好地描绘用户的日出行规律。出行链对应的时空变化关系如图1所示，时间层表示从开始到结束的时间变化，Δ表示行驶和停留时间段，表示到达和离开时间点，空间层表示出行过程的空间变化，表示节点间的行驶里程。

本文基于出行链模型描述车辆日出行行为特性。按照出行链结构和区域功能，将区域分为住宅区、工作区和商业区等功能区，并做以下假设：一天内EV初始位置和最终到达都属于住宅区；不考虑充电桩因素对EV充电的影响；不考虑不同功能区之间路径因素的影响。

1.1.1 出行活动类型

相关调查表明[10]，居民出行活动以简单链(起讫点均为H，链长为3)为主。考虑主要出行目的，忽略可能会在某处短暂停留的情况，将出行目的分为5类：回家(Home, H)、工作(Work, W)、社交休闲(Social and Recreational, SR)、购物吃饭(Shopping& Eating, SE)和其他活动(Other, O)。本文考虑最长含3个行驶目的地的出行链结构，其结构可分为简单链和复杂链2种模式，如图2所示。

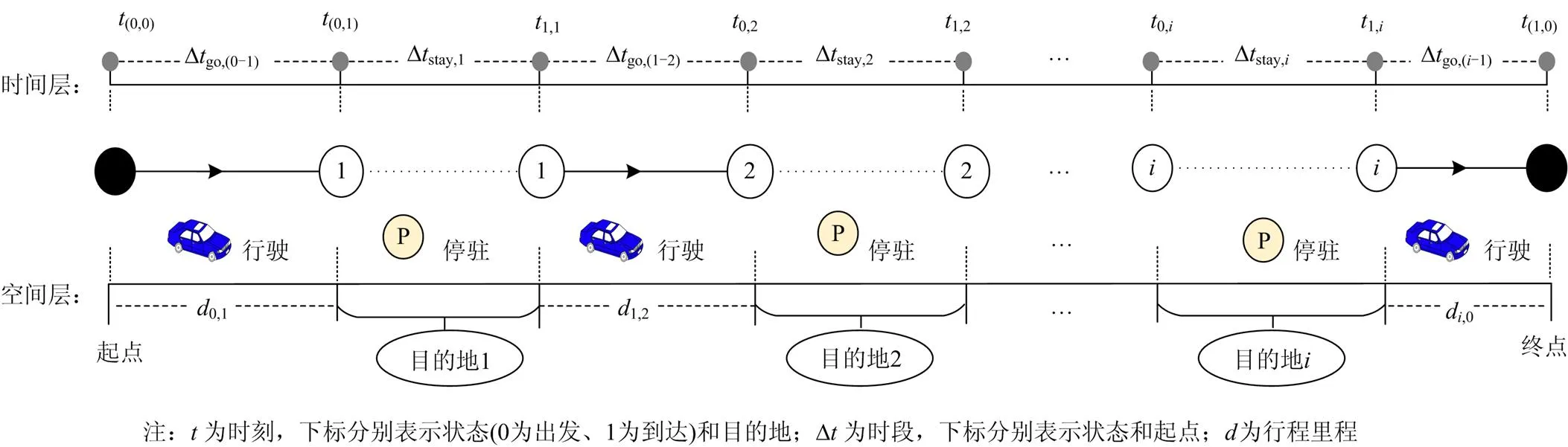
图1 出行链对应的时空变化

图2 简单和复杂出行链结构模型

1.1.2 区域转移概率

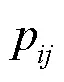
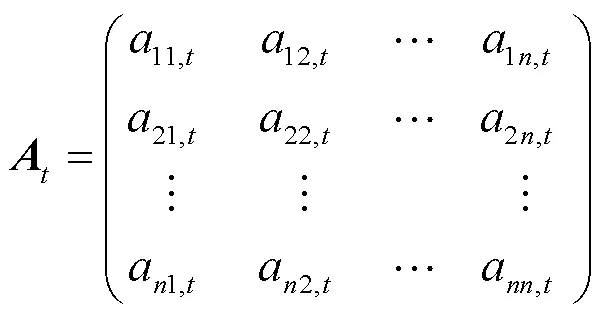
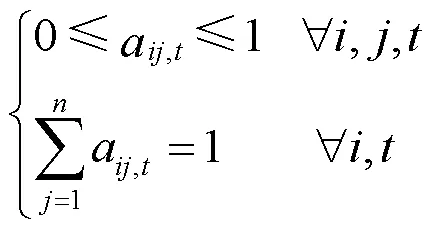
1.1.3 出行时间

EV用户每日起始出行时刻可近似为正态分布[18]，其概率密度函数为

式中：s为起始出行时刻均值，s= 8.56；s为初始出行时刻方差，s= 1.57，单位为h。

出行链中途各类出行活动花费的时间(车辆停留的时间)呈现不同的概率分布特性。由美国家庭交通出行调查数据(National Household Travel Survey, NHTS)[19]数据统计可知，W及SR类型出行活动花费时间近似满足正态分布，SE、H及O类型出行活动花费时间近似满足指数分布，如式(6)。各类出行活动对应的均值与标准差拟合结果如表1所示。此处H类型出行活动指在家中短暂停留后继续当日出行，即不考虑出行链的起始点。

表1 各类出行活动停留时间概率分布拟合结果

1.2 EV电池最大载电量

为模拟EV充电行为，首先需要考虑季节温度对电池的影响，获得EV电池最大载电量。EV电池对温度具有较强的敏感性[20-21]，在不同温度下放电量如图3所示，电池的实际最大载电量会发生变化。设定25 ℃为参考温度，此时电池放电量为10 380 mAh，相对电量为100%。由图3可知，高于25 ℃时，电池实际最大载电量变化不明显；低于25 ℃时，随着温度降低呈明显下降趋势，0 ℃时电池放电量为8 200 mAh，相对容量仅为79.3%。

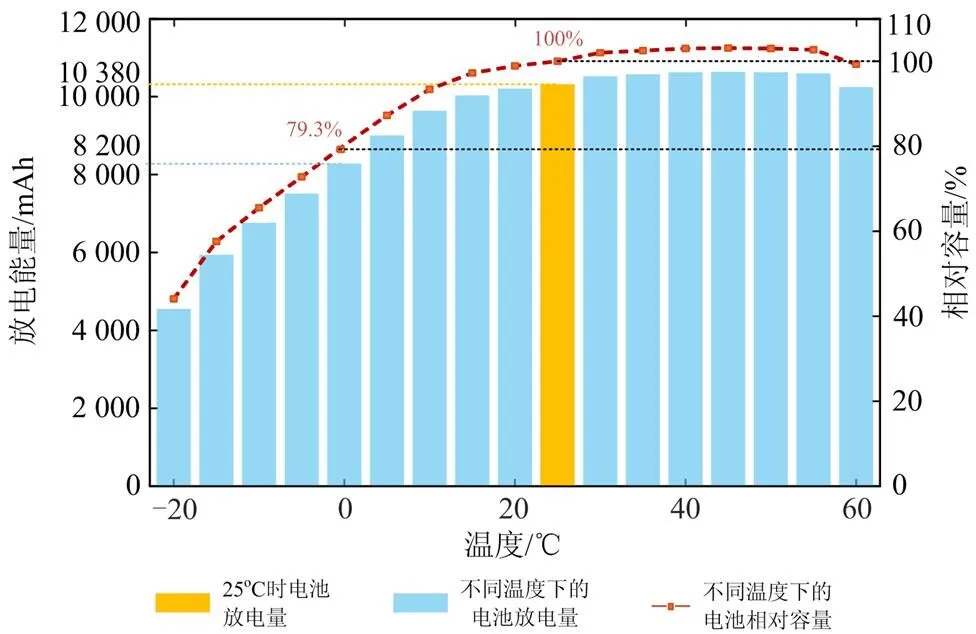
图3 不同温度下电池放电量

由图3可知，不同温度下电池实际最大载电量为

1.3 EV耗电量

计算行程过程中总耗电量1，由式(2)可知，1包括行程中的里程耗电量1_1以及空调耗电量1_2两部分。

1) 里程耗电量

每段行程行驶里程可近似满足对数正态分布[22]，其概率密度函数为

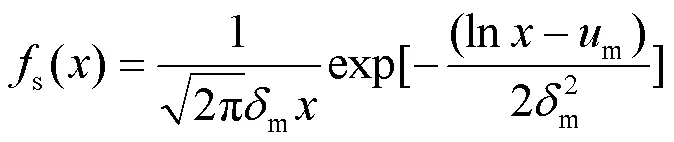
由式(10)可知，EV单位里程耗电量主要受到行程速度的影响。而暴雨暴雪、雾霾等天气会导致道路设施的可认知性降低和路面附着力下降，进而影响行车速度[22]。同时，雨雪雾天气也会影响道路交通流通性，限制汽车行驶速度。参考文献[23-25]中不同天气对应不同能见度和附着系数的车速限制建议，定制出具有季节性的安全行驶速度，如表2。

表2 不同季节不同天气下的安全行驶速度

2) 车载空调耗电量

参考文献[25]对不同温度下空调使用率进行调研，将相关数据拟合生成空调启动概率正态分布函数，如式(11)所示。

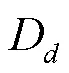
1.4 EV用户充电策略

由相关统计习惯可知，车主充电行为的灵活性、主观性较强[18]。大多数车主充电习惯采用灵活充电类型，即EV每到达一处目的地，只要该地配备有充电设施，就进行充电。本文假设，若某EV用户决定在某地进行充电，则在其到达该目的地时马上接入充电设施，连续充电直至达到理想电量或最大停留时间，如式(14)所示。

2 基于Bass修正模型EV中长期负荷预测

为实现中长期负荷的预测，需要得知不同年份的EV保有量规模，本文建立Bass修正模型，以预测未来数年的电动汽车的保有量。

2.1 Bass修正模型

Bass模型主要是对创新产品、技术的采用和扩散进行市场占有率预测的模型，用来模拟新产品被用户接受的过程。基本表现形式为

上述模型并未涉及到价格对新产品扩散的影响方面，因此Frank Bass提出了修正Bass模型(Generalized Bass Model)[27]，在原模型的基础上引入修正系数()，用以反映多种价格因素对产品推广的影响，如式(16)、式(17)所示。

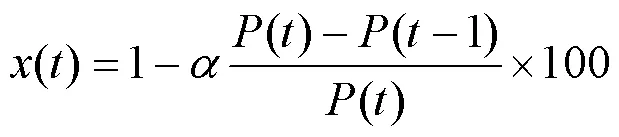
式中：()为时段新产品价格；为1%的价格增长造成的市场吸引力下降程度。

2.2 模型参数估计与修正

本文在Bass模型的基础上分析EV当前市场发展特性，考虑传统能源汽车竞争、城市GDP发展、政策与油价等多种因素的影响，对模型系数进行估计与修正。

1) 模仿系数()的修正

购买决策受社会系统内部因素包括其他消费者对EV的使用反馈以及EV基础设施影响，这一部分消费者主要是由模仿系数体现，也被称作“内部影响系数”，取值范围在0～1。参考文献[18, 28-29]，类比充电便利模型刻画满意度与EV渗透率对电动汽车发展的影响，定义模仿系数为

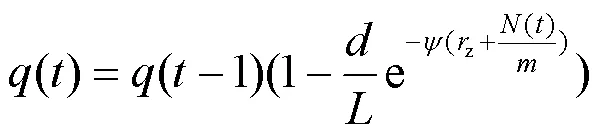
式中：()为时段(第年)模仿系数；为电动私家车续航里程；为电动私家车平均日行驶里程；z为车桩比；()/为渗透率；为调节因子。

2) 创新系数()的修正

EV的消费者中有一部分人群的购买决策不受包括其他消费者和EV基础设施等在内的社会系统内部因素的影响[30]，而是有赖于大众媒体的宣传，由创新系数来体现，也被称作“外部影响系数”，取值范围在0～1之间。考虑到宣传效应过程会存在一定滞后性，人群对EV接受程度的增量与宣传力度成正比[31]，因此定义创新系数为

3) 价格系数()的修正

目前常规能源汽车仍然是汽车市场的主体，其价格因素对EV发展有较大的竞争影响，同时城市GDP发展水平也间接影响着购买者对价格因素的敏感度。因此，采用文献[32]的定义方式建立修正系数()，如式(20)。

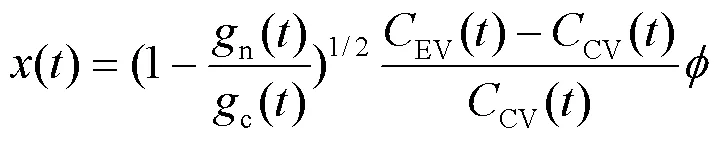
式中：EV()和CV()分别为EV总成本和常规能源汽车总成本折算到购买初年的现值；为成本影响系数，为负值。总成本包括购买成本及使用成本。

购买成本在含税价格的基础上扣除了补贴金额以及折现后的车辆残值，如式(22)。

使用成本是指使用期限内能耗与保养费用的贴现值之和，如式(23)。

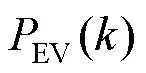
2.3 中长期EV负荷预测建模流程

由Bass修正模型预测未来不同年份的EV保有量规模，根据不同年份的保有量更新短期负荷预测模型，实现EV中长期负荷预测。具体流程如图4。

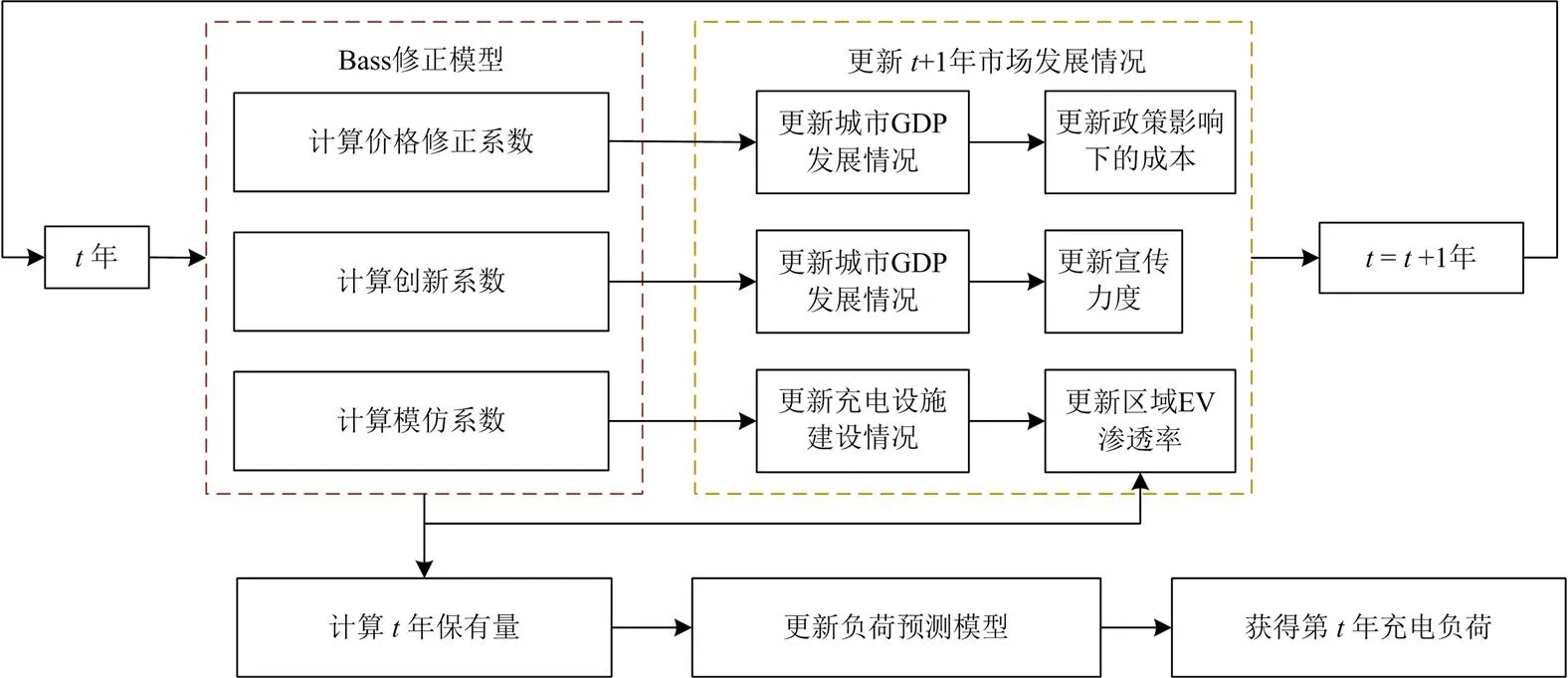
图4 中长期EV负荷预测流程

3 考虑季节特性的多时间尺度EV充电负荷预测仿真流程

由短期负荷预测模型得出不同季节特性下EV日内充电负荷曲线，再根据Bass修正模型预测未来十年内EV保有量，更新短期负荷预测模型的保有量可计算出未来10年不同季节下的日负荷曲线，预测流程如附图1所示。

为了获得EV用户每段行程的剩余电量SOC，需要确定EV电池的实际最大载电量、行程的里程耗电量以及空调耗电量。根据温度确定电池的实际最大载电量，结合单辆车空调的启用采取判定方法求得空调耗电量，确定行程里程耗电量需要计算EV在日内充电负荷的时空分布。因此，对输入规模的EV进行出行行为仿真：

首先，设定以生活区为起始点，离开家时的电池初始电量为最大载电量的95%，对车辆进行初始出行时刻抽取。

然后，从区域转移概率矩阵中提取终点落在各个区域的概率，对终点进行抽样，由起止区域得到这一段行驶里程。

最后，根据表3道路路径使用频率占比抽取行程的道路等级，结合设定的安全速度获得行程的耗电量。路径使用频率占比计算流程如附图2。

由初始电量和损耗电量差值得到电池剩余电量，再抽取停留时间后，根据车主充电习惯决定是否在此充电。当车辆完成最后一次行程后，更新各区域的充电负荷，当完成所有EV行为仿真后可得到本年该区总体及各功能区日充电负荷曲线。根据不同季节下温度和安全行驶速度，得出不同季节特性的EV短期(日内)充电负荷的时空分布，更新不同年份的保有量得到该区整体的中长期(未来十年)充电负荷曲线从而实现不同时间尺度下的负荷预测。

表3 行程道路路径使用频率占比

4 算例分析

4.1 参数设置

参考上海市气象统计局统计的2020年全年温度数据，按照时间划分为春秋季、夏季和冬季，再结合季节性气温特点，取20 ℃为典型常温(春秋季)天气，0 ℃和35 ℃分别为典型冬季和夏季气温。其中，电池相对容量百分数[25]：0℃=79.3%，20℃= 98.8%，35℃=103%。根据对应温度的空调启动概率，单辆车空调的启用采取判定方法：通过对单辆车生成服从(0，1)均匀分布的随机数，若<启动空调。

4.2 结果分析

4.2.1 EV保有量预测分析

对比不同城市GDP发展水平、宣传力度、油价增幅和政策补贴退坡对EV保有量预测的影响。

在图5中，默认条件为上海市GDP背景，油价增幅为6%，政策补贴退坡力度为20%，宣传力度为0.4。对上述单一条件设置变量对比分析其对EV保有量增长的影响，其他为默认条件。

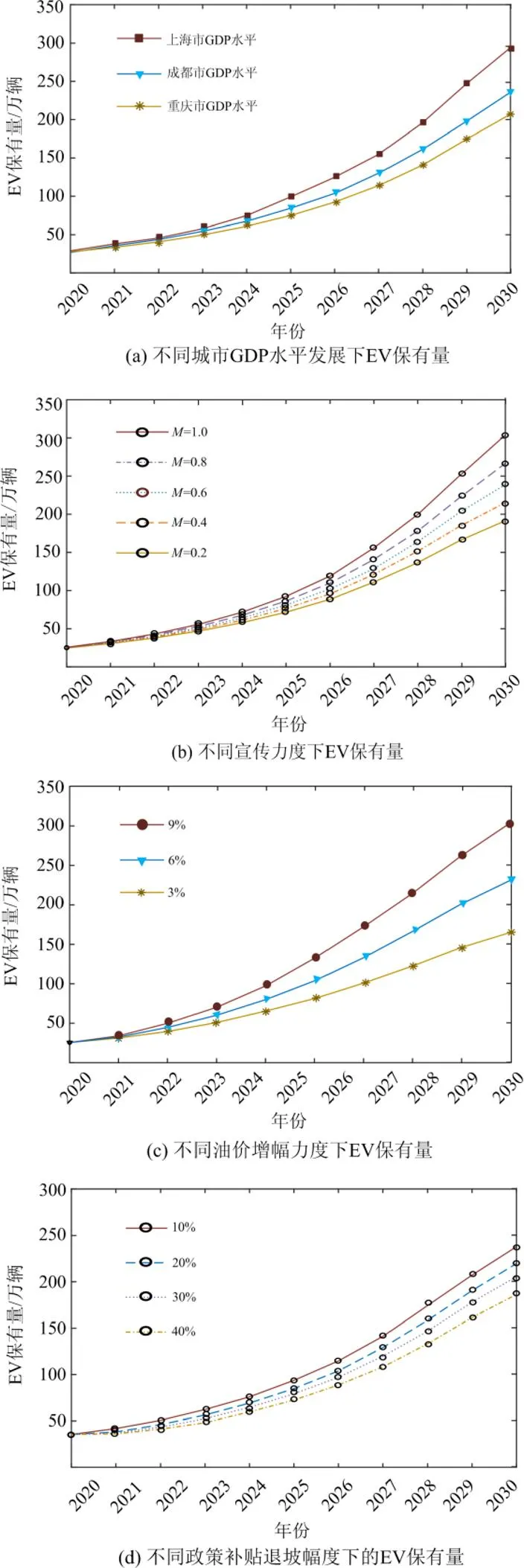
图5 不同因素影响下的EV保有量预测

如图5所示，相较于油价与政策退坡幅度，在短期内城市GDP水平、宣传力度对EV保有量的影响较小，但随着时间推移，两者对电动汽车的增幅作用会逐渐显现。宣传力度越大，对电动汽车的推广作用越明显，城市GDP水平越高，人们购买电动汽车的意愿更强。同样也可看出政策退坡幅度越大、油价增幅力度越弱，电动汽车保有量的增长幅度就越小。在中长期以后上述不同因素对电动汽车保有量增长均会产生较明显影响。

从整体增长态势来看，相较于中期的快速增长，在后期由于电动汽车市场潜量逐渐趋于饱和，基础充电设施建设发展也相对保持稳定，使得整体保有量的增长稍有放缓，趋于市场发展成熟阶段。

4.2.2 EV多时间尺度负荷预测分析

在保有量预测数据的基础上，对多时间尺度的EV充电负荷进行预测。将不同年份的EV保有量预测结果作为相应年份的EV数量，针对不同功能区，进行不同季节下的EV充电负荷预测。一方面可以从短期日内分析不同功能区的时空分布特性与季节差异；另一方面可以从较长时间尺度下(中长期)分析EV充电负荷增长趋势及季节特性对EV充电负荷的影响。

图6为2030年各功能区EV充电负荷曲线。可以看出：居民生活区负荷需求最大，呈双高峰分布，高峰时段集中在12：00和21：00附近；工作区次之，高峰时段集中在08：00附近；其他区域负荷需求都较小，且分布规律有明显差异。

由于季节因素对于一个区域内不同功能区的差异不大，本节的EV中长期负荷预测以整个区域的负荷为对象，分析2021—2030年春秋季、夏季和冬季的典型日的负荷需求情况。图7为2030年该区域在不同季节下整体负荷曲线对比。

图6 2030年各功能区EV充电负荷预测曲线

图7 2030年不同季节典型日充电负荷对比

由图7可以看出，EV充电负荷具有较明显的季节特性。冬季和夏季负荷需求要大于春秋季，主要是由于冬季温度较低夏季气温较高，空调使用率较高，使得EV的空调耗电量显著增大。同时，由于温度较低的环境下电池性能受到的影响较高温环境下更明显，因此，冬季EV充电需求量也比夏季略高。

图8为该区域在2021—2030年春秋季、夏季、冬季典型日负荷需求预测曲线，同样可以看出EV充电负荷在冬季最高，春秋季最低，而图8中三者增长幅度相差不大，主要是因为EV充电负荷增长主要取决于EV保有量的增长。

图8 2021—2030年不同季节充电负荷典型日预测

整理图8中各季节的峰值数据，得到该区域在2021—2030年不同季节典型日的负荷峰值及峰值差，如图9所示，其中天气A、B对应的速度如表2。由图9可以看出，冬季节典型日的负荷峰值最大，夏季次之，春秋季最低。同时行车速度的降低也会使得EV单位里程耗电量增加，导致负荷需求增大。由不同季节的峰值差可以看出冬季和夏季之间负荷峰值差距较小，因为常温下电池性能趋于最佳且不涉及空调的耗电量，充电负荷相对较小，因此冬季和夏季的负荷峰值明显高于春秋季。

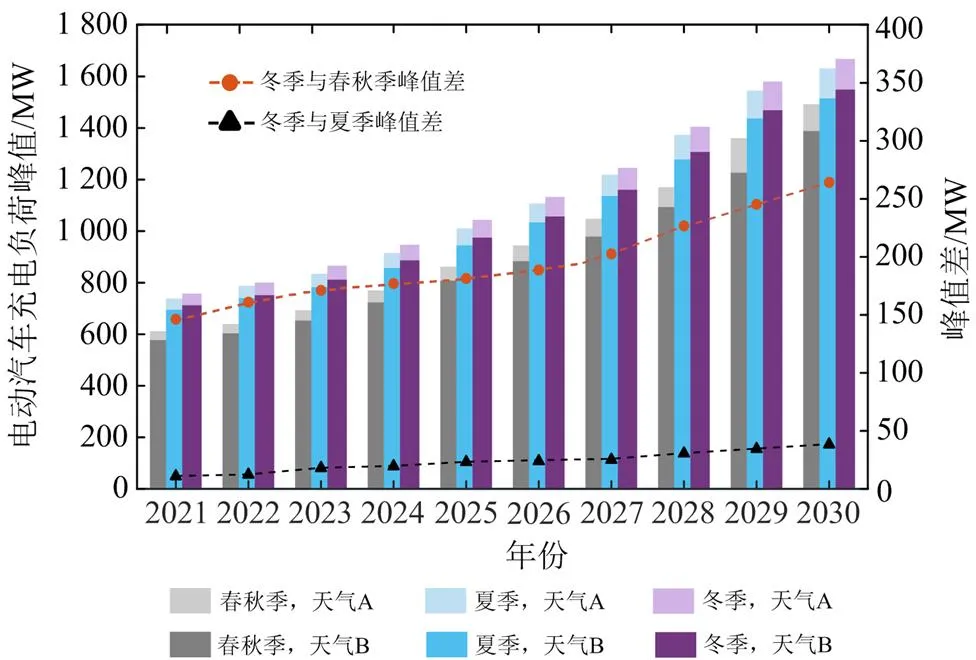
图9 2021—2030年不同季节典型日负荷峰值

5 结论

本文建立了考虑季节特性的短期EV充电负荷模型，在此基础上，结合Bass修正模型将预测时间从短期延展至中长期，进而实现了不同季节下短期和中长期EV充电负荷预测，得到多时间尺度下EV充电负荷预测曲线，通过算例仿真得到以下结论：

1) 所提考虑多因素影响的Bass修正模型可以有效预测不同年份的EV保有量，反映城市GDP发展水平、油价增幅力度、宣传力度以及补贴力度等因素对未来的EV保有量发展的影响。可为决策者制定EV推广政策提供一定的参考依据。

2) 相比于常规的单一时间尺度负荷预测模型，建立了考虑季节特性的多时间尺度负荷预测模型。一方面，可以有效刻画在较长时间尺度下不同季节特性的EV充电负荷特性；另一方面，通过Bass修正模型，实现了从短期到中长期的多时间尺度负荷预测。预测时间范围更为全面，对未来智能电网的EV充电设施建设规划与配网调度更具参考意义。

附录

附表1 车辆相关参数

附表2 不同年份的最大市场潜量

附表3 2020年全国及相关城市GDP

由于汽车市场尚未饱和，常规能源汽车保有量以增长率=0.15−0.012逐年增长至饱和[18]，EV最大市场潜量为常规能源汽车总数的90%。根据《上海市新能源汽车产业大数据研究报告2019》，截至2019年底，上海市注册常规能源汽车数量约为290万辆，EV约26万辆。由此，根据以上数据和关系计算出每年的潜在市场数量。

参考《中共上海市委关于制定上海市国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建设》、国家统计局发布的《2020年国民经济和社会发展统计公报》、国家统计局局长邱晓华主持的未来15年中国生产力发展的展望与宏观研究报告以及GDP研究权威人士许宪春的《未来15年中国生产力发展的展望与预测》等文件资料，设置未来10年全国GDP以λ＝0.02+0.006的增速逐年增长，上海市GDP在未来10年内以每年6个百分点进行增长。

附表4 上海市未来不同年份的车桩比

根据上海市新能源汽车公共数据网(SHEVDC)与上海市新能源汽车公共数据采集与监测研究中心，预测初年(2020年)上海市车桩比为0.8。参考《上海市促进电动汽车充(换)电设施互联互通有序发展暂行办法》、《上海市推进新型基础设施建设行动方案(2020—2022年)》以及《中共上海市委关于制定上海市国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建设》，基于建设规划目标，设置未来10充电桩配套EV建设发展，车桩比发展：z=0.8+0.05(当z＞1.2时，保持z不变)。

附图1 EV充电负荷预测流程图

Attached Fig. 1 Flow chart of EV charging load forecasting

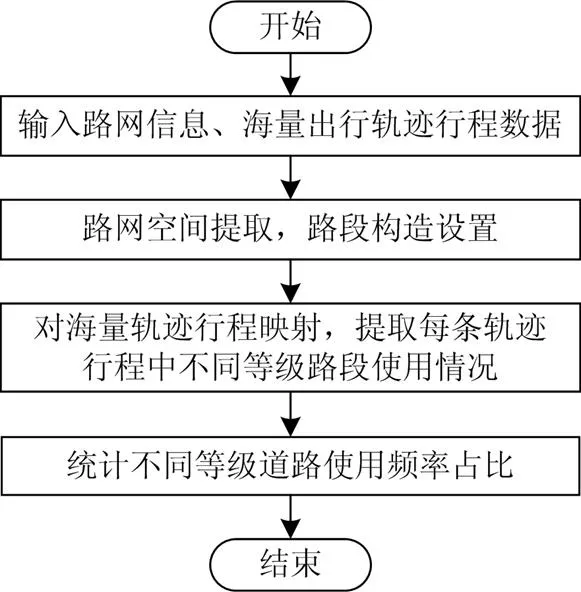
附图2 不同等级道路路径使用频率占比计算流程图

Attached Fig. 2 Flow chart for calculating the proportion of the use frequency of road paths of different grades

文中式(10)所定义一级、二级和三级道路参考现行交通部施行的《国家公路工程技术标准》，仿真所用一级、二级和三级道路数据，是通过对路网开源网站(OPENSTREETMAP)中某局部地区交通路网的数据处理所获得。海量行驶轨迹大数据来源为“滴滴订单轨迹开源数据”。

参考文献

[1] 檀勤良, 代美, 梅书凡. 考虑电动汽车碳配额及需求响应的电力系统调度研究[J]. 电网与清洁能源, 2021, 37(7): 79-86.

TAN Qinliang, DAI Mei, MEI Shufan. Research on electric vehicle carbon quota and demand response in electric power system dispatching[J]. Advances of Power System & Hydroelectric Engineering, 2021, 37(7): 79-86.

[2] 姚颖蓓, 陆建忠, 傅业盛, 等. 华东地区电动汽车发展趋势及用电需求预测[J]. 电力系统保护与控制, 2021, 49(4): 141-145.

YAO Yingbei, LU Jianzhong, FU Yesheng, et al. Electric vehicle development trends and electricity demand forecast in East China[J]. Power System Protection and Control, 2021, 49(4): 141-145.

[3] BloombergNEF electric vehicle outlook 2020[EB/OL]. [2020]. https:// about. bnef. com/ electric-vehicle-outlook/.

[4] CAI H, CHEN Q, GUAN Z, et al. Day-ahead optimal charging/discharging scheduling for electric vehicles in microgrids[J]. Protection and Control of Modern Power Systems, 2018, 3(1): 93-107.

[5] 马玲玲, 杨军, 付聪, 等. 电动汽车充放电对电网影响研究综述[J]. 电力系统保护与控制, 2013, 41(3): 140-148.

MA Lingling, YANG Jun, FU Cong, et al. Review on impact of electric car charging and discharging on power grid[J]. Power System Protection and Control, 2013, 41(3): 140-148.

[6] 侯慧, 徐焘, 柯贤彬, 等. 电动汽车快充对配电网的风险研究[J]. 电力系统保护与控制, 2019, 47(16): 87-93.

HOU Hui, XU Tao, KE Xianbin, et al. Research on risks of electric vehicle charging to distribution network[J]. Power System Protection and Control, 2019, 47(16): 87-93.

[7] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42.

LUO Zhuowei, HU Zechun, SONG Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011, 35(14): 36-42.

[8] 张洪财, 胡泽春, 宋永华, 等. 考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(1): 13-20.

ZHANG Hongcai, HU Zechun, SONG Yonghua, et al. A prediction method for electric vehicle charging load considering spatial and temporal distribution[J]. Automation of Electric Power Systems, 2014, 38(1): 13-20.

[9] 钱甜甜, 李亚平, 郭晓蕊, 等. 基于时空活动模型的电动汽车充电功率计算和需求响应潜力评估[J]. 电力系统保护与控制, 2018, 46(23): 127-134.

QIAN Tiantian, LI Yaping, GUO Xiaorui, et al. Calculation of electric vehicle charging power and evaluation of demand response potential based on spatial and temporal activity model[J]. Power System Protection and Control, 2018, 46(23): 127-134.

[10] 陈丽丹, 聂涌泉, 钟庆. 基于出行链的电动汽车充电负荷预测模型[J]. 电工技术学报, 2015, 30(4): 216-225.

CHEN Lidan, NIE Yongquan, ZHONG Qing. A model for electric vehicle charging load forecasting based on trip chains[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 216-225.

[11] TANG D, WANG P. Probabilistic modeling of nodal charging demand based on spatial-temporal dynamics of moving electric vehicles[J]. IEEE Transactions on Smart Grid, 2015, 7(2): 627-636.

[12] 张谦, 王众, 谭维玉, 等. 基于MDP随机路径模拟的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2018, 42(20): 65-72.

ZHANG Qian, WANG Zhong, TAN Weiyu, et al. Spatial-temporal distribution prediction of charging load for electric vehicle based on MDP random path simulation[J]. Automation of Electric Power Systems, 2018, 42(20): 65-72.

[13] 李含玉, 杜兆斌, 陈丽丹, 等. 基于出行模拟的电动汽车充电负荷预测模型及V2G评估[J]. 电力系统自动化, 2019, 43(21): 88-102.

LI Hanyu, DU Zhaobin, CHEN Lidan, et al. Trip simulation based charging load forecasting model and vehicle-to-grid evaluation of electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(21): 88-102.

[14] 李晓辉, 李磊, 刘伟东, 等. 基于动态交通信息的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2020, 48(1): 117-125.

LI Xiaohui, LI Lei, LIU Weidong, et al. Spatial-temporal distribution prediction of charging load for electric vehicles based on dynamic traffic information[J]. Power System Protection and Control, 2020, 48(1): 117-125.

[15] 龙雪梅, 杨军, 吴赋章, 等. 考虑路网-电网交互和用户心理的电动汽车充电负荷预测[J]. 电力系统自动化, 2020, 44(14): 86-93.

LONG Xuemei, YANG Jun, WU Fuzhang, et al. Electric vehicle charging load prediction considering road network-grid interaction and user psychology[J]. Automation of Electric Power Systems, 2020, 44(14): 86-93.

[16] ZHANG H C, TANG W Z, HU Z C, et al. A method for forecasting the spatial and temporal distribution of PEV charging load[C] // Proceedings of 2014 IEEE PES General Meeting Conference, July 27-31, 2014, National Harbor, MD, America:1-5.

[17] 邢强, 陈中, 黄学良, 等. 基于数据驱动方式的电动汽车充电需求预测模型[J]. 中国电机工程学报, 2020, 40(12): 3796-3813.

XING Qiang, CHEN Zhong, HUANG Xueliang, et al. Electric vehicle charging demand forecast model based on data-driven mode[J]. Proceedings of the CSEE, 2020, 40(12): 3796-3813.

[18] 于海东, 张焰, 潘爱强. 电动汽车充电负荷中长期推演模型[J]. 电力系统自动化, 2019, 43(21): 80-93.

YU Haidong, ZHANG Yan, PAN Aiqiang. Mid-long term deduction model of electric private car charging load[J]. Automation of Electric Power Systems, 2019, 43(21): 80-93.

[19] US Department of Transportation, Federal Highway Administration. 2017 national household travel survey [EB/OL]. [2017]. http: // nhts. ornl.gov.

[20] 张元星, 李斌, 颜湘武, 等. 基于电池模型的电动汽车充电故障监测与预警方法[J]. 电力系统保护与控制, 2021, 49(10): 143-154.

ZHANG Yuanxing, LI Bin, YAN Xiangwu, et al. Monitoring and early warning method of EV charging failure based on a battery model[J]. Power System Protection and Control, 2021, 49(10): 143-154.

[21] 孙庆, 杨秀金, 代云飞, 等. 温度对磷酸铁锂电池性能的影响[J]. 电动自行车, 2011(9): 22-27.

SUN Qing, YANG Xiujin, DAI Yunfei, et al. The influence of temperature on the performance of lithium iron phosphate batteries[J]. Electric Bicycle, 2011(9): 22-27.

[22] 王睿, 高欣, 李军良, 等. 基于聚类分析的电动汽车充电负荷预测方法[J]. 电力系统保护与控制, 2020, 48(16): 37-44.

WANG Rui, GAO Xin, LI Junliang, et al. Electric vehicle charging demand forecasting method based on clustering analysis[J]. Power System Protection and Control, 2020, 48(16): 37-44.

[23] LAURIKKO J, GRANSTROM R, HAAKANA A. Realistic estimates of EV range based on extensive laboratory and field tests in Nordic climate conditions[C] // Electric Vehicle Symposium and Exhibition, November 17-20, 2013, Barcelona, Spain: 1-12.

[24] LI H M, WANG Q Q, XIONG W X. New model of travel-time prediction considering weather conditions: case study of urban expressway[J]. Journal of Transportation Engineering, Part A: Systems, 2021, 147(3): 967-975.

[25] 王海玲, 张美霞, 杨秀. 基于气温影响的电动汽车充电需求预测[J]. 电测与仪表, 2017, 54(23): 123-128.

WANG Hailing, ZHANG Meixia, YANG Xiu. Electric vehicle charging demand forecast based on the influence of temperature[J]. Electrical Measurement & Instrumentation, 2017, 54(23): 123-128.

[26] 张恒嘉. 基于实证的纯电动汽车性能评估方法和普及可能性研究[D]. 武汉: 武汉理工大学, 2014.

ZHANG Hengjia. Study on the assessing methods and the possibility of popularity of pure electric vehicles based on the empirical test[D]. Wuhan: Wuhan University of Technology, 2014.

[27] BASS F M, KRISHNAN T V, JAIN D C. Why the Bass model fits without decision variables[J]. Marketing Science, 1994, 13(3): 203-223.

[28] 杨威, 向月, 刘俊勇, 等. 基于多代理技术的电动汽车规模演化模型[J]. 电网技术, 2017, 41(7): 2146-2154.

YANG Wei, XIANG Yue, LIU Junyong, et al. Multi-agent modeling for the scale evolution of plug-in electric vehicles[J]. Power System Technology, 2017, 41(7): 2146-2154.

[29] 周昊, 刘俊勇, 刘友波, 等. 基于系统动力学的电动汽车规模推演分析与仿真[J]. 电力系统及其自动化学报, 2017, 29(8): 1-7.

ZHOU Hao, LIU Junyong, LIU Youbo, et al. Analysis and simulation of electric vehicles scale evolution based on system dynamics[J]. Proceedings of the CSU-EPSA, 2017, 29(8): 1-7.

[30] 曾鸣, 曾繁孝, 朱晓丽, 等. 基于Bass模型的我国电动汽车保有量预测[J]. 中国电力, 2013, 46(1): 36-39.

ZENG Ming, ZENG Fanxiao, ZHU Xiaoli, et al. Forecast of electric vehicles in China based on Bass model[J]. Electric Power, 2013, 46(1): 36-39.

[31] EPPSTEIN M J, GROVER D K, MARSHALL J S, et al. An agent-based model to study market penetration of plug-in hybrid electric vehicles[J]. Energy Policy, 2011, 39(6): 3789-3802.

[32] 龙子泉, 常静敏, 陈植元. 激励政策对新能源汽车推广的影响研究—基于修正Bass模型的实证分析[J]. 科技管理研究, 2016, 36(4): 138-144.

LONG Ziquan, CHANG Jingmin, CHEN Zhiyuan. Effects of incentives to the promotion of new energy vehicles—based on the empirical analysis of modified Bass model[J]. Science and Technology Management Research, 2016, 34(4): 138-144.

Multi-time-scale electric vehicle load forecasting model considering seasonal characteristics

NIU Mutong, LIAO Kai, YANG Jianwei, XIANG Yueping

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China)

Current research on electric vehicle (EV) charging load forecasting is mostly focused on a short-term single time-scale, and few consider the differences of electric vehicle charging load in different seasons on a longer time scale. Therefore, a multi-time-scale electric vehicle load forecasting method considering seasonal characteristics is proposed. First, a short-term day-to-day electric vehicle charging load prediction model is established taking into account the influence of seasonal characteristics on the initial battery power, mileage power and air-conditioning power consumption of the EV, and combining time and space distribution rules. Secondly, in order to show the characteristics of multiple time scales from short-term (within a day) to medium-and long-term (years), a modified Bass model that takes into account the influence of multiple factors is built to predict the EV holdings in different years in the future. Combined with short-term EV, the charging load forecasting model can be extended to mid-to-long-term EV charging load forecasting, thereby achieving multi-time-scale EV load forecasting and integrating short-term and mid-to-long-term. Finally, through simulation verification with the temperature information and driving data of Shanghai, the results demonstrate that the proposed model is able to effectively predict the EV development trend over the next few years and the EV charging load under multiple time scales considering seasonal characteristics.

electric vehicle; load forecasting; Bass model; multi-time-scale; seasonal characteristics

10.19783/j.cnki.pspc.210628

国家自然科学基金项目资助(51977180)

This work is supported by the National Natural Science Foundation of China (No. 51977180).

2021-05-25；

2021-08-12

牛牧童(1997—)，男，硕士研究生，主要研究方向为电动汽车充电负荷预测；E-mail: niumutong@my.swjtu.edu.cn

廖 凯(1988—)，男，通信作者，博士，副教授，主要研究方向为电力系统稳定分析与控制、新能源电力系统保护与控制；E-mail: liaokai_lk@hotmail.com

杨健维(1983—)，女，博士，副教授，主要研究方向为电动汽车优化调度。E-mail: jwyang@swjtu.edu.cn

(编辑 葛艳娜)