基于电磁时间反转理论的非全程同杆双回线故障测距

商立群，吉 宁

基于电磁时间反转理论的非全程同杆双回线故障测距

商立群，吉 宁

(西安科技大学电气与控制工程学院，陕西 西安 710054)

为了解决非全程同杆双回输电线路故障测距中存在的双端数据不同步以及伪根识别的问题，首先利用故障区段识别函数组的正负相位特性确定故障发生的区段。在确定故障区段的基础上，采用了一种基于电磁时间反转的频域前行电流法进行故障测距。然后将故障区段两侧的电压、电流解耦后进行快速傅里叶分解，提取工频分量下的电流前行波并求取共轭。最后计算假设的各个故障点处的电流有效值大小，当有效值为最小时，该点即为故障点。仿真结果表明：该方法不需要双端数据的同步，没有伪根识别问题，同时也不受过渡电阻和故障类型的影响，能实现对非全程同杆双回线的准确故障定位。

非全程同杆双回输电线路；故障测距；电磁时间反转；六序分量法

0 引言

同杆并架双回输电线路在考虑经济性的同时，大幅度提高了线路的输电容量，且具有较高的供电可靠性。在实际运用中，考虑到地理因素以及不同用电需求的影响，出现了一种只有部分线路同杆并架的非全程同杆双回线路。非全程同杆并架输电线路与全程同杆并架输电线路相比，在线路结构和故障类型方面，都有较大差异。目前，对于普通的同杆并架输电线路故障测距已有大量研究[1-9]，对于非全程同杆线路的研究还比较少，现有的故障测距方法是否同样适用于非全程同杆并架输电线路还有待考证。故障测距方法根据算法原理的不同可分为行波法和故障分析法。故障分析法分为单端法和双端法，单端法在测距过程中仅用线路一端所测数据信息，测距精度很大程度上受到运行方式、过渡电阻等因素影响[10]；双端法需要传送双端数据的通信通道，数据严格同步实现困难，增加了硬件成本[11]，目前非全程同杆双回线测距方法主要是对传统双端法的改进。文献[12]针对双端数据的不同步问题，移动不同步时间范围内的双端数据，进行搜索匹配，实现数据的同步化，但此方法在同步匹配时需合理选择其搜索步长，采样频率的选择对测距结果的精度有很大的影响；文献[13]提出了基于线路参数矩阵的沿线电压和新的解耦方法的测距方法。这两种方法对于同步性都有较高的要求，且前一种方法构造方程比较繁琐，第二种方法虽然利用耦合部分两端电压和电流的故障各序分量来构造测距函数，构造方程的过程比较简单，但是需要使用双回线的双端电气量，对同步的要求更高。另外由于沿线电压分布不是严格的线性分布，双端法测距中常会出现伪根问题，文献[14]针对传统伪根识别方法中存在的问题，采用两个模分量建立故障定位函数，判断真实的故障位置。

时间反转(Time Reversal, TR)具有时空聚焦的特性，且这种特性对环境具有自适应的能力。其最早应用于声学领域，其后应用于电磁波，根据麦克斯韦方程组时间反转不变性，在雷电定位上取得了良好的结果[15]；文献[16]在频域中证明了电磁时间反转(Electromagnetic Time Reversal, EMTR)理论应用于无损线路故障测距的正确性；文献[17]针对涉及损耗的电磁传播不满足严格的时间反转不变性，提出了3种不同的反向传播模型；文献[18-20]研究了利用时间反转理论来定位输电线路故障点的方法。本文针对非全程同杆双回输电线路故障测距中存在的双端数据同步和伪根识别等问题，采用基于EMTR理论的频域前行电流法进行故障测距，验证EMTR理论在非全程同杆双回线中的适用性和有效性。

1 非全程同杆双回线的故障区段判别

图1 非全程同杆双回输电线路示意图

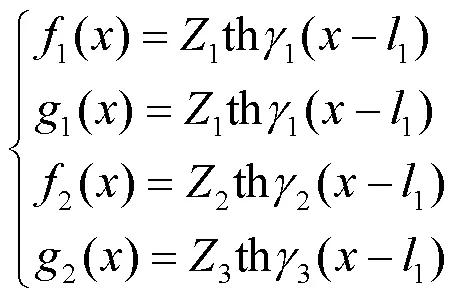
1) 单回线故障

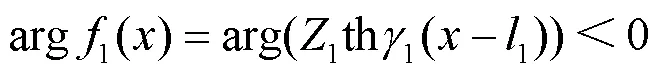
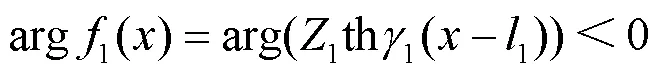
2 EMTR理论在故障测距上的应用

电磁时间反转理论的核心是对所测量的信号基于时间方向的逆转，即

多导体有损传输线的电压波动方程如式(10)所示。

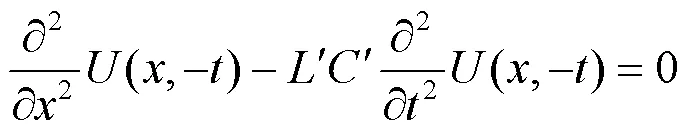
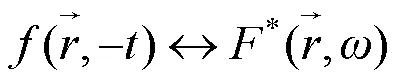
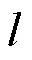
图2 无损线路故障附加网络

Fig. 2 Fault additional network for lossless line

“大夫说你身体虚弱，要好好调理。”他扶起我，双目相交，他眼中依然是一片不见底的漩涡，让我不由自主地沉溺。

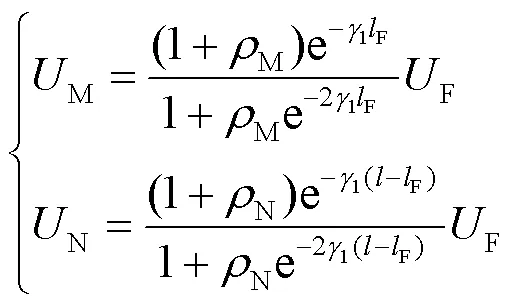
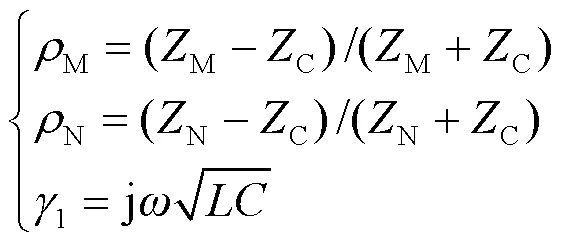
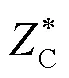
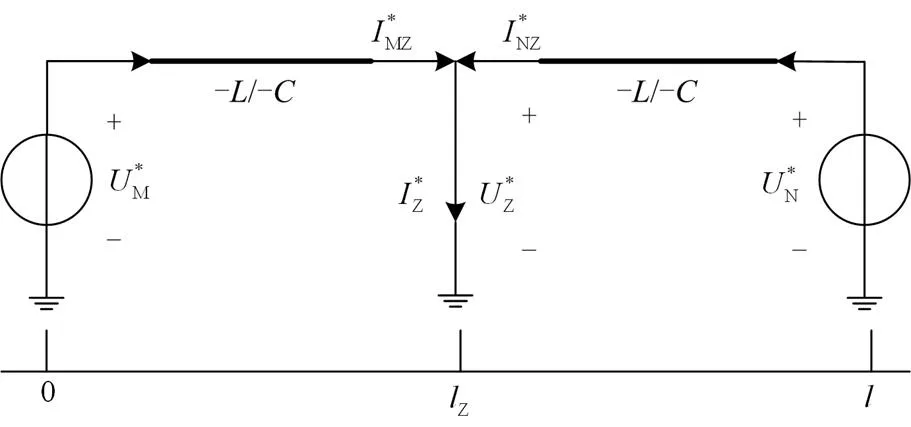
图3 假设故障处的无损镜像线路

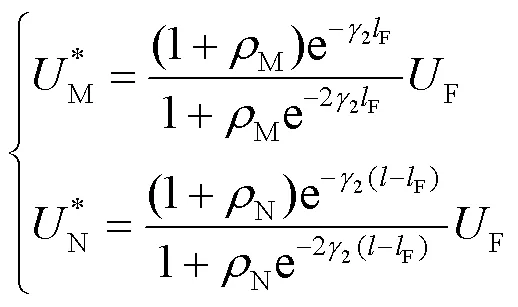
线路两端的电流如式(17)所示。

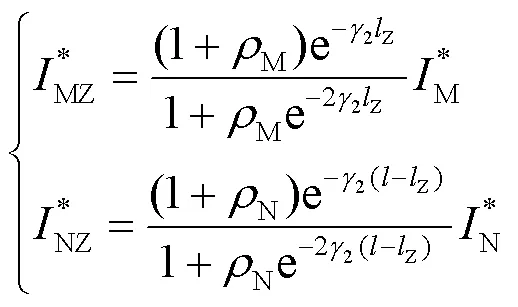
联立式(16)、式(17)和式(18)可得

最终，可得到故障位置的总电流表达式为

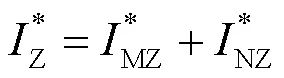
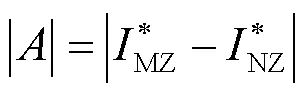
3 基于EMTR的频域前行电流法故障测距

EMTR方法采用线路双端电压、电流量进行测距，采用频域前行电流法能够有效解决双端数据不完全同步采样所造成的误差问题，具体测距步骤如下。

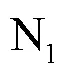
该故障测距算法的流程如图4所示。

图4 故障测距流程图

Fig. 4 Flow chart of fault location

4 仿真验证

4.1 模型参数及仿真过程

1) 故障发生在单回线区段

假设在距离线路T点100 km处的单回线区段发生单相接地故障，过渡电阻为15W。设置的故障开始时间为0.1 s，采集0.08～0.16 s时间内M端和N端的电压、电流数据，采样频率为12.8 kHz。利用M端数据推得T点处的电压、电流值后，利用对称分量法分别对N端和T点处的电压和电流数据进行解耦，对得到的正序电压、电流值经过FFT后，提取工频正序分量。

在镜像线路上每隔5 m假设一次故障，利用式(23)计算故障电流的有效值，图5给出了沿线各处假设故障电流有效值。由图5可知，横坐标在99.73 km处为故障电流最小值点，此点即为最终故障测距结果。

图5 单回线侧故障测距结果

2) 故障发生在双回线区段

假设在距离线路M侧200 km的双回线部分发生单相接地故障，记录M端与N端处的电流数据和电压数据。从N端推算出T点处的电压、电流量后，利用六序分量法分别对M侧和T点处的电压、电流数据进行解耦处理，对同向正序分量进行FFT后，提取工频下的同向正序电压、电流分量。

在镜像线路上每隔10 m假设一次故障，利用式(23)求假设故障电流的有效值，图6给出了沿线各处假设故障电流有效值。由图6可知，横坐标在200.54 km处为故障电流最小值点，即最终故障测距结果为200.54 km。

图6 双回线侧故障测距结果

4.2 单回线区段不同故障类型测距结果

4.3 双回线区段不同故障类型测距结果

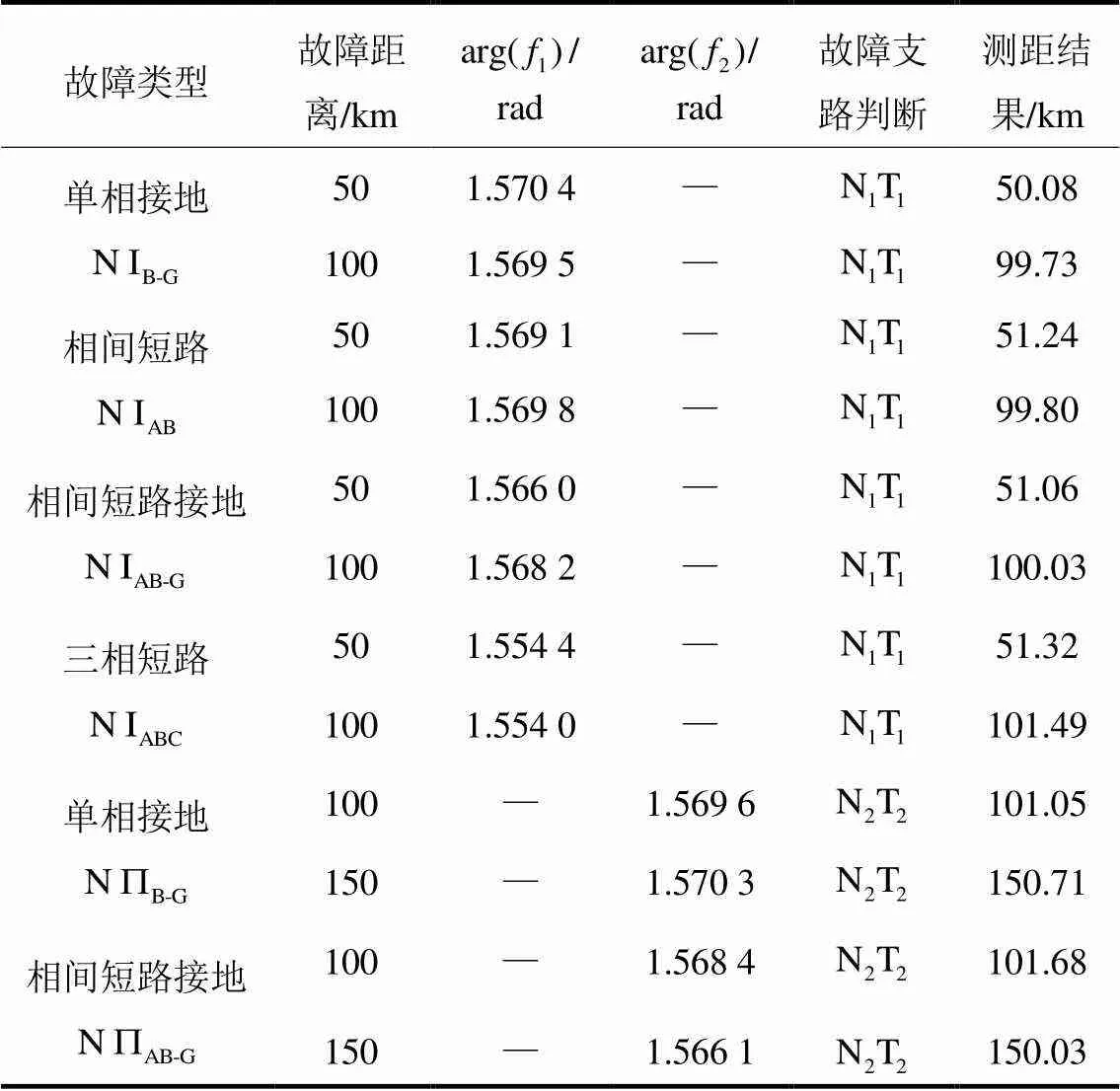
表1 单回线路段不同故障类型测距结果

表2 双回线路段不同故障类型测距结果

4.4 不同过渡电阻的影响

不同过渡电阻条件下，测量的电压、电流大小有所不同，所得的电流前行波大小也有所不同。但本文所采用的基于电磁时间反转方法是基于电磁场能量变换的一种故障定位方法，建立镜像线路时，假设故障电流是由故障点对地电压进行表示的，其对地电压即过渡电阻两端的电压，通过传输方程计算沿线各假设点的电流大小，无需知道实际的过渡电阻值，因而理论上算法不受过渡电阻的影响。在不同故障类型下，对过渡电阻分别为15 Ω、50 Ω、100 Ω情况下进行验证，故障测距结果如表3所示。从表3可以看出，过渡电阻不同不会对测距结果造成明显的影响。

表3 不同过渡电阻时测距结果

4.5 故障相角的影响

表4 电源在不同初相角时故障测距结果

4.6 双端数据不同步的影响

对于双端测距法，为实现线路两端的同步采样，可以采用GPS技术，但是测距结果也比较依赖于GPS的可靠性，且其成本较高。非线性元件的动态时延往往也会对故障定位的精度产生一定的影响。

本文采用基于电磁时间反转的频域前行电流法进行故障测距，利用工频下的电压、电流数据进行计算，电压、电流幅值大小不受时间的影响，理论上测距结果不受双端数据不同步的影响。对不同步的电压、电流数据进行故障测距，假设在单回线区段距离N1端50 km处发生单相接地故障，测距结果如表5所示。从仿真结果可以看出，两侧的不同步时间即使达到0.05 s，对测距结果也没有太大影响，因此各种非线性元件带来的传输延时误差不会对此方法的测距结果造成影响。

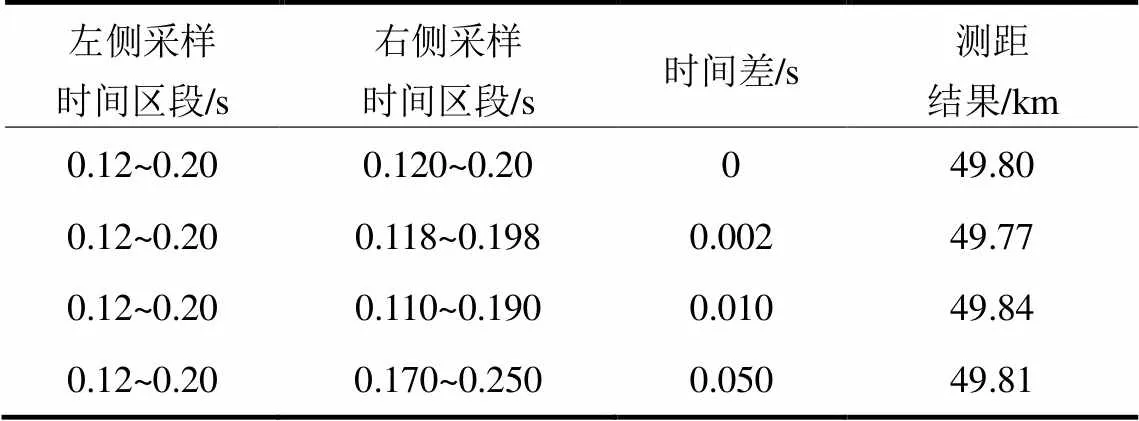
表5 双端数据不同步时故障测距结果

5 结论

本文将EMTR方法用于非全程同杆双回线路的故障测距，针对非全程同杆双回线的结构特点和参数特征，先利用故障测距函数的相位阶跃特点进行故障区段的判别，再通过基于EMTR理论的频域前行电流法进行故障测距。仿真结果表明：基于EMTR理论的测距方法在非全程同杆双回线的单回线区段和双回线区段都有较高的测距精度，且不受过渡电阻、故障类型和故障相角的影响。此外，与传统双端法相比，频域前行电流法无需双端数据的同步。基于EMTR的故障测距方法具有广阔的应用前景。

[1] 朱忆洋, 都洪基, 赵青春. 不对称参数同杆双回线选相方法研究[J]. 电力系统保护与控制, 2017, 45(15): 133-139.

ZHU Yiyang, DU Hongji, ZHAO Qingchun. Research on phase selection for double-circuit lines on the same tower with asymmetrical parameters[J]. Power System Protection and Control, 2017, 45(15): 133-139.

[2] 许侃, 范春菊. 不同电压等级部分耦合线路的单回线故障分析[J]. 电力系统自动化, 2015, 39(12): 81-87.

XU Kan, FAN Chunju. Single-circuit fault analysis of partially coupled lines with different voltage levels[J]. Automation of Electric Power Systems, 2015, 39(12): 81-87.

[3] 陶彩霞, 杜雪, 高锋阳. 基于经验小波变换的混合输电线路单相接地故障测距[J]. 电力系统保护与控制, 2021, 49(10): 105-112.

TAO Caixia, DU Xue, GAO Fengyang. Single-phase to ground fault location of hybrid transmission lines based on empirical wavelet transform[J]. Power System Protection and Control, 2021, 49(10): 105-112.

[4] 杨韬, 罗萍萍, 龚锦霞, 等. 基于改进无迹卡尔曼滤波的短线路同杆并架双回线参数辨识[J]. 电力系统保护与控制, 2021, 49(5): 36-45.

YANG Tao, LUO Pingping, GONG Jinxia, et al. Parameter identification of short parallel double-lines based on a modified unscented Kalman filter[J]. Power System Protection and Control, 2021, 49(5): 36-45.

[5] LI Zhenxing, WAN Jialing, WANG Pengfei, et al. A novel fault section locating method based on distance matching degree in distribution network[J]. Protection and Control of Modern Power Systems, 2021, 6(2): 253-263.

[6] 刘朕志, 舒勤, 韩晓言, 等. 基于行波模量速度差的配电网故障测距迭代算法[J]. 电力系统保护与控制, 2015, 43(8): 88-93.

LIU Zhenzhi, SHU Qin, HAN Xiaoyan, et al. An iterative fault location algorithm using the difference of wave velocity between zero mode component and aerial mode component of traveling wave[J]. Power System Protection and Control, 2015, 43(8): 88-93.

[7] JAMALI S, BAHMANYAR A, RANJBAR S. Hybrid classifier for fault location in active distribution networks[J]. Protection and Control of Modern Power Systems, 2020, 5(2): 84-92.

[8] 宋国兵, 索南加乐, 许庆强, 等. 基于双回线环流的时域法故障定位[J]. 中国电机工程学报, 2004, 24(3): 24-29.

SONG Guobing, SUONAN Jiale, XU Qingqiang, et al. A novel time-domain algorithm for locating faults on parallel transmission lines by circulating circuit[J]. Proceedings of the CSEE, 2004, 24(3): 24-29.

[9] 刘千宽, 李永斌, 黄少锋, 等. 基于双端电气量的同杆平行双回线单线故障测距[J]. 电网技术, 2008, 32(3): 27-30.

LIU Qiankuan, LI Yongbin, HUANG Shaofeng, et al. Single-line fault location of parallel double transmission line on same tower based on two-terminal electrical quantities[J]. Power System Technology, 2008, 32(3): 27-30.

[10] 赵冠琨, 贾科, 陈金锋, 等. 基于断路器重合闸的柔性直流输电线路单端故障测距方法[J]. 电力系统保护与控制, 2021, 49(7): 48-56.

ZHAO Guankun, JIA Ke, CHEN Jinfeng, et al. A single terminal fault location method for a DC transmission line based on circuit breaker reclosing[J]. Power System Protection and Control, 2021, 49(7): 48-56.

[11] 孙广, 王阳, 薛枫, 等. 特高压直流输电线路改进双端行波故障定位方法研究[J]. 电力系统保护与控制, 2020, 48(14): 113-120.

SUN Guang, WANG Yang, XUE Feng, et al. Research on an improved double-terminal traveling wave fault location method for UHVDC project[J]. Power System Protection and Control, 2020, 48(14): 113-120.

[12] 索南加乐, 宋国兵, 许庆强, 等. 利用两端非同步电流的同杆双回线故障定位研究[J]. 电工技术学报, 2004, 19(8): 99-106.

SUONAN Jiale, SONG Guobing, XU Qingqiang, et al. Research on fault location of double circuit lines on the same tower using two-terminal asynchronous currents[J]. Transactions of China Electrotechnical Society, 2004, 19(8): 99-106.

[13] 朱忆洋, 都洪基. 不对称参数同杆并架双回线故障选相和测距方法的研究[D]. 南京: 南京理工大学, 2017.

ZHU Yiyang, DU Hongji. Research on the method of phase selection and location for double circuit transmission lines with asymmetrical parameters on the same tower[D]. Nanjing: Nanjing University of Science and Technology, 2017.

[14] 王守鹏, 商立群, 张杰. 同杆并架双回线故障测距的研究[D]. 西安: 西安科技大学, 2015.

WANG Shoupeng, SHANG Liqun, ZHANG Jie. Research on fault location of double circuit lines on the same tower[D]. Xi'an: Xi'an University of Science and Technology, 2015.

[15] LUGRIN G, MORAN M, RACHIDI F, et al. On the location of lightning discharges using time reversal of electromagnetic fields[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(1): 149-158.

[16] RAZZAGHI R, LUGRIN G, MANESH H, et al. An efficient method based on the electromagnetic time reversal to locate faults in power networks[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1663-1673.

[17] RAZZAGHI R, LUGRIN G, RACHIDI F, et al. Assessment of the influence of losses on the performance of the electromagnetic time reversal fault location method[J]. IEEE Transactions on Power Delivery, 2017, 32(5): 2303-2312.

[18] 张希鹏, 邰能灵, 郑晓冬, 等. EMTR理论在电力系统线路故障测距中的应用基础I: 理论部分[J]. 电网技术, 2020, 44(3): 845-854.

ZHANG Xipeng, TAI Nengling, ZHENG Xiaodong, et al. Application of EMTR theory in fault location of power system I: theory part[J]. Power System Technology, 2020, 44(3): 845-854.

[19] 张希鹏, 邰能灵, 郑晓冬, 等. 基于 WEMTR 的柔性直流输电线路故障测距[J]. 电工技术学报, 2019, 34(3): 589-598.

ZHANG Xipeng, TAI Nengling, ZHENG Xiaodong, et al. Fault location in VSC-HVDC transmission lines based on WEMTR[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 589-598.

[20] 艾轩源, 刘辉, 曹宝玉, 等. 基于EMTR和PSO的输电线路故障定位[J]. 湖北工业大学学报, 2019, 34(5): 56-59.

AI Xuanyuan, LIU Hui, CAO Baoyu, et al. Fault location of transmission line based on EMTR and PSO[J]. Journal of Hubei University of Technology, 2019, 34(5): 56-59.

[21] 葛耀中. 新型继电保护和故障测距的原理和技术[M]. 2版. 西安: 西安交通大学出版社, 2007.

[22] 张莹, 梁军. 复杂输电线路故障测距算法研究[D]. 济南: 山东大学, 2017.

ZHANG Ying. LIANG Jun. Research on fault location algorithm for complex transmission lines[D]. Jinan: Shandong University, 2017.

[23] 林富洪, 王增平. 采用同向正序基频分量的双回线故障测距原理[J]. 中国电机工程学报, 2011, 31(4): 93-98.

LIN Fuhong, WANG Zengping. The principle of double-circuit line fault location based on co-directional positive sequence fundamental frequency components[J]. Proceedings of the CSEE, 2011, 31(4): 93-98.

Fault location based on electromagnetic time reversal for non whole journey double circuit line on the same pole

SHANG Liqun, JI Ning

(School of Electrical and Control Engineering, Xi’an University of Science and Technology, Xi’an 710054, China)

There is a problem of double end data asynchrony and pseudo-root identification in the fault location of non whole journey double circuit line on the same pole. To solve this problem, first, the fault section is determined using the positive and negative phase characteristics of the fault section identification function group. To determine the fault section, a frequency domain forward current method based on electromagnetic time reversal is proposed for fault location. Then, the voltage and current on both sides of the fault section are decoupled and fast Fourier decomposition is performed. The current forward traveling wave of the power frequency component is extracted and its conjugate value is obtained. Finally, the current effective value at each assumed fault point is calculated. When the calculated effective value of current is the smallest, the corresponding point is the fault point. The proposed method does not need two terminal data synchronization. The simulation results show that there are no problems such as pseudo root identification and the algorithm is not affected by transition resistance, fault type or initial phase angle. Accurate fault location results can be obtained for either a double circuit line or single circuit line section.

non whole journey double circuit line on the same pole; fault location; electromagnetic time reversal; six-sequence component method

10.19783/j.cnki.pspc.210755

陕西省自然科学基础研究计划项目资助 (2021JM393)

This work is supported by the Natural Science Basic Research Program of Shaanxi Province (No. 2021JM393).

2021-06-25；

2021-11-15

商立群(1968—)，男，博士，教授，主要研究方向为电力系统分析与控制、电力系统电磁暂态仿真、电力系统过电压防护；E-mail: shanglq@xust.edu.cn

吉 宁(1996—)，男，硕士研究生，主要研究方向为电力系统故障测距。E-mail: 1259578696@qq.com

(编辑 许 威)