基于自适应干扰观测的连续有限时间末段突防制导律

王 洋，王 震，陈明淑

(西京学院理学院，西安 710000)

0 引言

随着导弹防御技术的发展，出现了诸如PAC-3[1]，Aster-15[2]以及RAM[3]等众多高性能末段拦截系统，因此，导弹在弹道末段受到的拦截威胁越来越大。此外，大量实际目标都具备一定的机动能力，而目标机动可能会降低导弹打击精度。因此，同时考虑具备机动能力的突防导弹、拦截器以及目标构成的三攻防对抗场景，对突防导弹设计高精度及强突防制导律具有重要实用意义。

比例制导律(Proportional Navigation Guidance Law,PNGL)由于结构简单、易于实现而得到广泛应用，但存在以下不足：1) 面对强机动目标时，PNGL制导精度降低；2) 由于未考虑突防，因此采用PNGL的导弹末段弹道平直，易于被成功拦截。

有限时间控制可以有效提升传统渐近式控制的收敛精度与速度[4]。近年来，出现了许多基于有限时间稳定性理论设计的制导方法。文献[5]基于李雅普诺夫稳定理论提出了有限时间制导律(Finite-Time-Convergent Guidance Law,FTCGL)；文献[6-7]提出了基于滑模的FTCGL；文献[5-7]的FTCGL都采用了切换项抑制目标机动带来的扰动影响。然而，切换项带来两方面问题：一是抖振问题；二是需要已知目标机动加速度上界，而目标机动难以提前获悉，即使已知也很保守。

近年来,许多文献采用干扰观测器(Disturbance Observer,DO)估计目标机动，从而避免使用切换项。文献[8-9]采用扩张状态观测器(Extended State Observer,ESO)。但是ESO基于渐近稳定理论设计，无法保证估计误差收敛到零。因此，这些基于ESO的FTCGL的制导精度会受到ESO估计误差的影响。文献[10]采用非光滑干扰观测器(Non-Smooth Disturbance Observer,NSDO)设计FTCGL。NSDO虽然可以保证估计误差收敛到零，但是NSDO需要已知目标机动加速度变化率的上界。显然，在实际工程中，目标机动加速度变化率上界也难以预知。

此外，与PNGL的设计思路相同，前述文献[5-10]提出的FTCGL只考虑制导精度，因此其弹道平缓，易受拦截。近年来，针对如何提高导弹末段突防能力的问题，有文献开展了研究。文献[11]为空舰导弹设计了螺旋机动俯冲制导律；文献[12]基于滑模算法设计了导弹机动突防策略；文献[13]采用包含时变附加项的比例导引律追踪虚拟目标,从而实现螺旋俯冲机动。但是，文献[11,13]方法只适用于慢速或非机动目标,文献[12]的策略方法没有严格证明稳定性。

基于以上问题，本文基于自适应干扰观测器及有限时间稳定性理论，为突防弹设计一种新型机动突防制导律，所提方法有如下优势：

1) 基于自适应有限时间干扰观测器对目标机动加速度进行观测，可有限时间补偿目标机动影响，且无需已知目标机动加速度的上界信息;

2) 通过有限时间机动衰减设计保证制导精度不受所设计的附加机动突防的影响;

3) 基于估计目标加速度以及突防机动连续化设计，保证了制导加速度连续变化。

1 问题描述

突防弹、拦截器及目标三方对抗关系如图1所示。

图1 突防弹、拦截器及目标三方对抗关系Fig.1 Penetration-intercepting offensive and defensive confrontation

图1中：M，T及I分别表示突防弹、目标及拦截器，其位置分别为(xM,yM)，(xT,yT)以及(xI,yI)；速度分别为VM，VT及VI；θM，θT与θI分别为突防弹、目标及拦截器的弹道倾角；qM与qI分别为突防弹与拦截器的视线角；rMT与rMI分别为突防弹与目标及突防弹和拦截器的相对距离。本文的变量均为标量。

可以建立如下突防弹、目标以及拦截器位置变化方程

(1)

(2)

(3)

突防弹-目标相对运动如下

(4)

拦截器-突防弹相对运动如下

(5)

(6)

式中,ATλ=ATcos(qM-θT)，为目标法向机动加速度。

期望目标 为突防弹M设计控制加速度AM，保证：1) 有限时间内VλM→0；2) 无需已知目标机动加速度上界信息；3)突防弹的弹道摆动机动；4) 控制加速度AM连续变化。

2 相关引理

本章由引理1及引理2给出后文需要用到的自适应干扰观测及有限时间收敛相关理论。

引理1(自适应二阶滑模控制算法)[14]考虑如下的系统

(7)

式中:sgn()为符号函数;d0为干扰；自适应参数的变化律为

(8)

时变参数L0(t)的自适应律为

(9)

式中，p0为正常数。只要干扰d0是有界的，则s0将在有限时间内收敛到0。

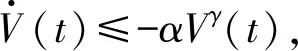
V(t)=0t≥tr

(10)

式中,收敛时间tr≤t0+V1-γ(0)/α(1-γ)。

3 突防制导律设计

3.1 自适应干扰观测器设计

基于引理1，设计如下自适应干扰观测器

(11)

(12)

L1(t)的自适应律为

(13)

式(11)干扰观测器的稳定性由定理1给出。

定理1针对满足假设1的式(4)制导系统，采用式(11)自适应干扰观测器，则存在有限时间tE满足

(14)

(15)

将式(6)及式(11)代入式(15)可得

(16)

(17)

综合式(16)及式(17)可得

(18)

同时，自适应参数满足

(19)

L1(t)的自适应律为

(20)

(21)

3.2 制导律设计

同时考虑打击精度及突防，设计滑模面为

(22)

式中：C(i=-n,…,-1,1,2,…,n)为非0整数；ϑ为非0常数；tM为机动截止时间。

针对滑模面s，设计机动突防滑模制导律

(23)

定理2针对满足假设1的式(4)制导系统，采用式(11)自适应干扰观测器及式(23)制导律，则存在有限时间tH可以保证法向相对速度

VλM=0t≥tH

(24)

同时式(23)给出的控制加速度AM连续变化。

证明过程如下。对滑模面s求左导数，可得

(25)

对滑模面s求右导数，可得

(26)

令AF=ϑsin(Cπ(t/tM))-ϑ(tF-t)Cπcos(Cπ(t/tM))/tM，易知AF在t=tM左右极限及函数值满足

AF+(tM)=AF+(tM)=AF(tM)=0

(27)

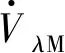
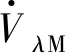
(28)

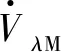
(29)

构造李雅普诺夫函数V1=s2/2，对V1求导，同时考虑式(18)，可得

(30)

(31)

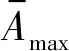
(32)

(33)

由于kσ>0且0<(σ+1)/2<1，同时V1(tE)是有界的，所以由引理2可知，存在有限时间tV1，使得

V1=s=0t>tV1。

(34)

随后，考虑以下两种情况。

情况1 当tV1≤tM，由式(34)及式(22)滑模面的定义可知，VλM=0,t>tM。

情况2 当tMtV1。

总结情况1及2可知

VλM=0t>max{tM,tV1}

(35)

由于max{tM,tV1}有限，所以可知式(24)成立。

4 仿真验证

4.1 单次对抗仿真

仿真中：突防弹的初始位置xM(0)=-5000 m，yM(0)=0 m;速度VM=500 m/s;弹道倾角θM(0)=qM(0);式(23)制导律及式(7)自适应干扰观测器参数kσ=1，σ=0.6，p1=0.7，L1(0)=15；机动参数ϑ=-30，C=5,tM=10。拦截器采用PNGL制导方法，比例系数取为5。拦截器的初始位置xI(0)=0 m，yI(0)=200 m，速度VI=600 m/s，弹道倾角θI(0)=qI(0)，目标的初始位置xT(0)=0 m，yT(0)=0 m，速度VT=50 m/s，弹道倾角θT=30°。目标机动加速度为AT=5sin(t/3),单位为m/s2。突防弹及拦截器的加速度上界都设置为500 m/s2。

为了对比突防效果，去掉式(23)制导律的机动项，形成如下的无机动有限时间制导律

(36)

(37)

采用式(23)无机动有限时间制导律进行对抗仿真(场景1)，结果见图2。由图2(a)可知，突防弹在未到达目标前就被拦截；由图2(b)可知，相对距离小于0.5 m，到达了被有效毁伤的距离；突防弹控制加速度见图2(c)，可知变化幅度很小。

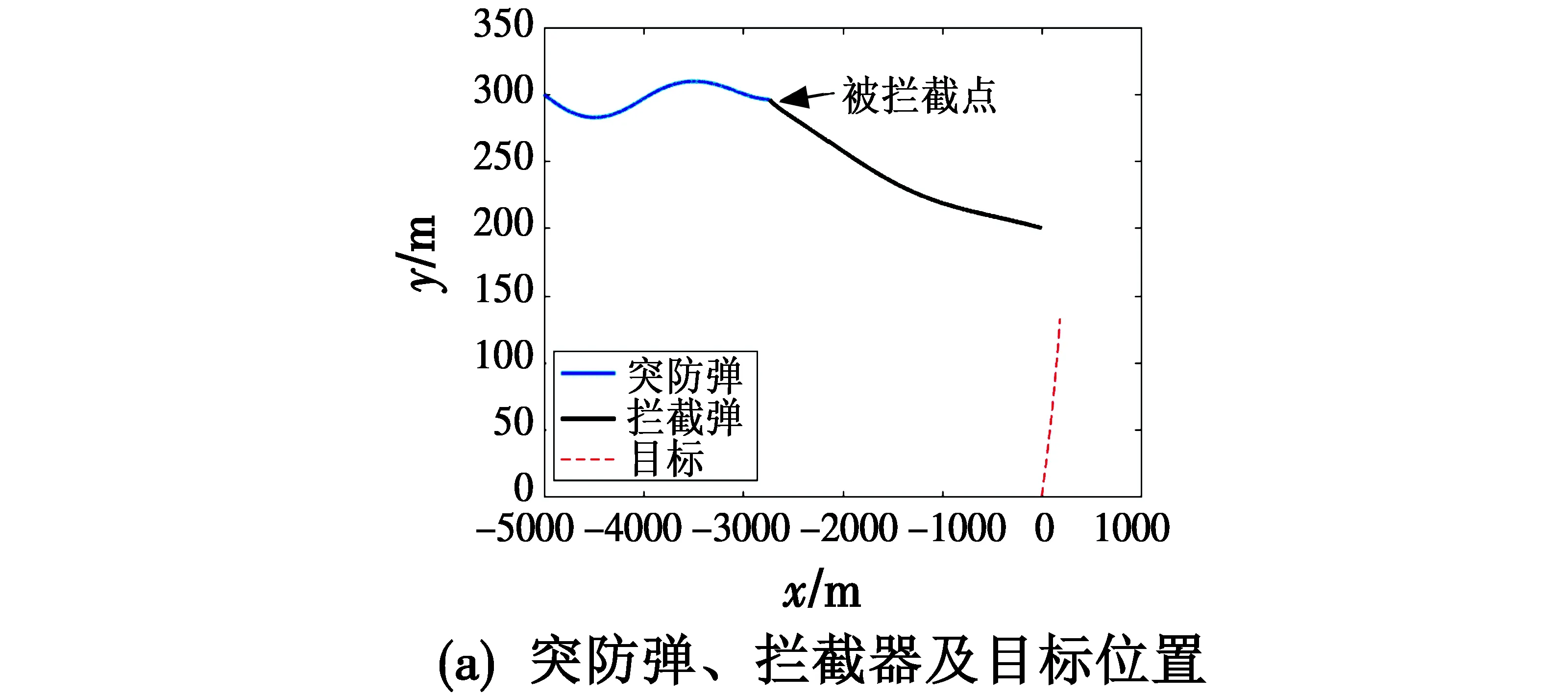
图2 场景1仿真结果(突防弹无机动)Fig.2 Simulation result of Case 1 when the missile is non-maneuvering

采用本文提出的式(23)机动制导律进行对抗仿真(场景2),仿真结果见图3。由图3(a)可知，突防弹成功突破了拦截；由图3(b)可知，拦截器与突防弹之间的最小距离大于20 m；突防弹的控制加速度见图3(c)，其摆动变化且幅度大，成功引起了拦截器的控制加速度饱和。另一方面，由图3(a)及图3(b)还可以看出，突防弹仍能保证突防弹与目标的相对距离接近零，保证了对目标的打击精度。自适应观测器的估计误差见图3(c)，自适应增益L1(t)的变化见图3(e)，其有界变化。此外，由图3(c)可知，所提出制导律的控制加速度连续变化。由图3(f)可知，所提出制导律的滑模面连续变化，且由于控制加速度连续变化，因此滑模面不存在抖振。

图3 场景2仿真结果(突防弹机动)Fig.3 Simulation result of Case 2 when the missile is maneuvering

4.2 多次对抗打靶仿真

考虑突防弹从不同的位置开始末段制导。定义i次打靶，i=1,2,…,60。对于第i次打靶，突防弹道初始位置为xM(0)=-5000 m，yM(0)=-3000+100im，速度VM=500 m/s,弹道倾角θM(0)=qM(0)。突防弹采用本文提出的式(23)机动制导律。拦截器采用PNGL制导方法。制导律参数及目标机动加速度与4.1节相同。

将拦截器及突防弹的脱靶量统计在图4中。由图4(a)可知，所有场景下拦截器对突防弹的脱靶量大于15 m，证明了突防弹可有效突防。由图4(b)可知，所有场景下突防弹相对目标的脱靶量都接近零，证明了所设计制导律对机动目标的高精度打击能力。

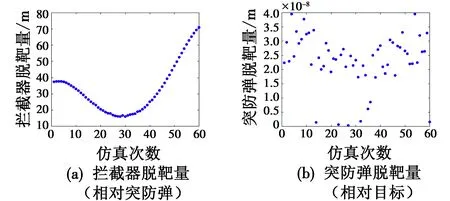
图4 突防弹机动时多次打靶结果统计Fig.4 Statistics of multiple shooting results when the missile is maneuvering

5 结论

本文提出了一种新型机动突防制导律，在保证突防弹末段打击精度的同时提高了突防能力。首先，基于自适应干扰观测器估计目标机动，在有限时间内补偿目标机动影响，且无需目标机动加速度上界信息;其次，通过机动衰减设计保证制导精度不受所设计的附加机动突防的影响;再次，基于估计目标加速度以及突防机动连续化设计，保证设计的制导律连续变化；最后，通过仿真验证了上述优点。