改进混沌粒子群算法的四旋翼PID姿态控制
2022-03-16张智轩伍鹏飞赵宏生
张智轩,李 涛,伍鹏飞,赵宏生
(南京信息工程大学自动化学院,南京 210000)
0 引言
四旋翼无人机由于成本低、机动能力强,近年来被广泛应用于多种场景,例如空中测绘、空中航拍、农业植保和地面物体跟踪等。四旋翼飞行控制系统作为四旋翼飞行器的控制中心,如何对四旋翼飞行器进行有效控制是当前国际多旋翼飞行控制领域研究的热点和难点。姿态控制是四旋翼飞行控制系统的重要组成部分,是平稳飞行的前提。PID控制操作简单,可以有效地控制四旋翼无人机,但其性能对参数的依赖较大[1-2],所以参数的选择至关重要。针对PID参数整定问题的智能优化算法有很多,如鸡群算法[3]、遗传算法[4]与粒子群算法[5-6](Particle Swarm Optimization,PSO)等。粒子群算法是一种新兴的基于群体智能的启发式全局搜索算法、操作简单、易于实现。而PID需要调节的参数只有3个,维数较少,因此,本文采用PSO算法求得最佳参数值,并将得到的参数值应用于PID控制器对四旋翼飞行器的姿态(翻转)和高度控制。
近年来,国内外很多学者为了提高传统PID参数整定技术的性能,各自利用粒子群算法对PID的参数进行了改进。胡文华等[7]为了解决控制参数优化问题,提出了一种变权重与杂交的粒子群优化算法:首先,根据迭代过程中粒子群中粒子与全局最优粒子间的距离大小动态改变惯性权重;其次,引入杂交进化增加粒子多样性,避免陷入局部最优;结果表明,该优化算法对参数的整定是有效的,能使四旋翼飞行器的控制品质得到保证和优化,提升设计效率。RAZA等[8]将PSO算法用于上肢康复机器人的PID控制验证了PSO算法的有效性和稳定性;胡丹丹等[9]将控制器的参数作为粒子群中的粒子进行迭代寻优,同时在传统的PSO算法基础上参考遗传算法,对适应度函数值较差的粒子进行交叉保优,仿真结果表明,优化后的控制器超调更小,调节时间更短;RONI等[10]采用遗传算法(GA)和PSO算法对三相MG系统的PID控制器进行优化;LI等[11]为了提高船舶跟踪自动驾驶仪的性能,提出了一种基于PSO优化的滑模变结构PID控制策略。
本文以X型变距、变转速四旋翼飞行器为研究对象,考虑到混沌序列摆脱停滞的出色表现,首先构造Logistic混沌序列代替粒子位置随机初始化,其次对粒子群算法的权重参数进行改进,增加了粒子多样性。比较其他混沌PSO算法,本文改进混沌PSO算法避免了算法陷入局部最优,改进了搜索速度和精度,并且构造简单。在四旋翼PID控制器参数调节的应用上,避免了人工调节参数的随机性,提高了控制器的可靠性。
1 四旋翼飞行器建模
为实现对小型四旋翼飞行器的有效控制,必须准确建立其在各种飞行状态下的数学模型。飞行器在飞行过程中不仅同时受到多种物理效应[12]的作用(空气动力、重力、陀螺效应和旋翼惯量矩等),还很容易受到气流等外部环境的干扰。四旋翼飞行器通常有两种模式,即“十”字型与X型[13]。本文选用X型四旋翼建立动力学模型,建立如图1所示的惯性坐标系E(oxyz)和四旋翼机体轴坐标系B(oxByBzB)。惯性坐标系取地球中心为坐标原点o,oz轴为沿地球自转轴方向,ox轴为赤道平面和本初子午面的交线,oy轴按右手规则确定。四旋翼机体坐标系以飞机重心为原点o,oxB轴为沿飞机横轴向右,oyB轴为沿飞机纵轴向前,ozB轴为沿飞机立轴(航向轴)向上。
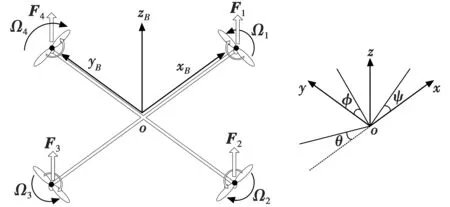
图1 惯性坐标系与机体坐标系Fig.1 Inertial coordinate system and body coordinate system
四旋翼飞行器采用4个螺旋桨作为驱动,螺旋桨对称地分布在机身周围,其推力可以通过改变电机转速来实现。四旋翼飞行器可以沿着机体的3个轴进行旋转或平移运动,因此在每个轴向上有两个自由度。四旋翼飞行器有6种飞行状态,即垂直运动、俯仰运动、滚转运动、偏航运动和前、后运动。
四旋翼飞行器建立合理准确的动力学数学模型,是飞行姿态精确控制的首要前提。因此,通常对飞行器进行一些合理假设:1)假设四旋翼飞行器为刚体,结构完全对称,将地面坐标系视为惯性坐标系;2)假设没有其他阻力影响和重力变化,阻力、重力始终保持不变;3)假设陀螺效应和空气动力扭矩效应均被抵消。基于以上假设,四旋翼飞行器模型可简化为
(1)
式中:φ,θ,ψ分别为滚转角、俯仰角和偏航角,是机体相对于惯性坐标系产生的角度;m为四旋翼飞行器的质量;Ix,Iy,Iz为飞行器转动惯量;g为所在地重力加速度;l为各个旋翼到机体坐标系原点的长度;U1~U4为各个通道的控制量,其表达式为
(2)
式中:F1,F2,F3,F4为对应电机的旋翼升力;Ω1,Ω2,Ω3,Ω4为对应电机的转速;k1,k2分别为四旋翼的升力系数和阻力系数。
2 改进混沌粒子群算法
2.1 粒子群算法
粒子群算法是一种基于进化计算技术的优化算法,是由鱼群学和鸟群学的研究发展而来的,由于其参数简单、收敛速度较快,而得到广泛应用。
PSO算法中,每一个粒子都被视为D维空间中的一个点[14]。粒子i的位置可以表示为Xi={xi1,xi2,…,xiD};粒子i的速度可以表示为Vi={vi1,vi2,…,viD};粒子i的个体最优解表示为Pi={pi1,pi2,…,piD};粒子i的全局历史最优解为Pg={pg1,pg2,…,pgD}。可更新粒子为
(3)
式中:i为粒子个数;viD为粒子i在D维空间的速度;xiD为粒子i在D维空间的位置;k为迭代次数;D为粒子的维度;c1,c2为粒子的学习因子;ω为粒子惯性权重;r1,r2为[0,1]之间的随机数。
本文算法的适应度函数选取ITAE误差准则,依照此准则设计的控制系统瞬态响应的振荡性小,且对参数具有良好的选择性。ITAE能够较好地抑制长时间存在的误差,其值越低,性能越好,其表达式为
(4)
式中:f为算法适应度函数,即ITAE误差方程;favg为算法适应度平均值;fmin为算法适应度最小值。
2.2 粒子群算法自适应惯性权重
KENNEDY和EBERHART于1995年首次提出原始版本粒子群算法之后,1998年ANGELINE又提出了一种改进的粒子群算法,增加了惯性权重ω这个新参数。
惯性权重对粒子群算法的性能至关重要,它负责平衡粒子群的全局搜索能力和局部搜索能力。大惯性权重有助于探索,但会使粒子长时间无法收敛到一个点;反之,较小的惯性权重会使粒子快速收敛,但有时会导致局部最优。在搜索过程中,每个粒子都会动态地改变其位置,因此,每个粒子都处于不同的复杂环境中,面临着不同的情况。因此,每个维度上的每个粒子在全局搜索能力和局部搜索能力之间存在着不同的权衡。对于目标函数值优于平均目标值的微粒,其对应的惯性权重因子较小,从而保护了该微粒,反之,对于目标函数值差于平均目标值的微粒,其对应的惯性权重因子较大,使得该微粒向较好的搜索区域靠拢。动态调整惯性权重的精细策略可以提高粒子群算法的性能。本文采用自适应动态惯性权重系数公式,其表达式为
(5)
式中,ωmax,ωmin分别为权重最大值和最小值,ωmax=0.9,ωmin=0.4。
2.3 Logistic混沌序列引入
混沌映射可以描述为一个具有确定性动力学行为的有界非线性系统,具有遍历性和随机性,它对于初始条件和参数非常敏感。也就是说,混沌的因果与初值的微小差异不成正比,这就产生了所谓的“蝴蝶效应”,即初值的微小变化会导致多次迭代后解的巨大差异。此外,混沌变量的轨迹可以遍历整个搜索空间。本文利用Logistic混沌映射方法生成均匀分布的初始粒子,以提高初始粒子群的质量,并在粒子群趋于停滞时重新初始化一定数量的粒子。
作为基础的混沌方法之一,Logistic映射在过去几十年中受到了研究者们的广泛关注。Logistic映射的分岔图见图2,其表达式见式(6)。
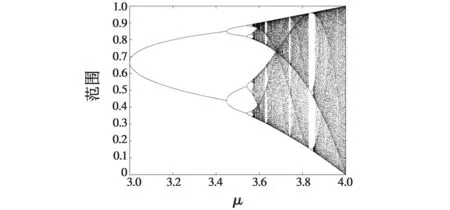
图2 Logistic映射分岔图Fig.2 Bifurcation diagram of Logistic equation
Li+1=μLi(1-Li)i=0,1,2,…
(6)
式中:Li表示第i个混沌变量,Li∈(0,1);初始值L0∈(0,1);μ为常数,也称为分叉系数,取值为4。
首先生成Li,根据式(6)更新Li,然后根据Xi=xi1+Li(xiD-xi1),将混沌序列映射到待优化的解空间。
3 改进粒子群算法PID控制器
改进粒子群算法的流程如下所述。
1) 初始化粒子群,随机产生所有粒子的位置和速度,并确定粒子的惯性权重。
2) 按照粒子群速度与位置公式更新粒子的速度和位置。
3) 将每个粒子代入仿真模型并计算对应的ITAE值。
4)计算所有粒子ITAE值的算术平均值,取偶数个ITAE值小于平均值的粒子直接进入下一次迭代。剩余粒子进行交叉选择,生成相同数量的子代,并与父代一起进行排序,取ITAE值更小的一半进入下一次迭代。
5) 将每一个粒子的适应值与该粒子所经历过的最优位置的适应值进行比较,如果更好,则将该粒子作为新的;对每个粒子,将其适应值与整个粒子群所经历过的最优位置的适应值进行比较,如果更好,则将该粒子作为新的;
6) 如果没有满足最终条件(适应值小于预设阈值或者超过最大迭代次数),则返回步骤2);否则,退出算法,输出寻优过程曲线和最优解。
利用改进混沌粒子群算法对PID的3个参数进行整定,再用整定之后的PID控制器来控制四旋翼飞行器,得到实际输出值与输入阶跃信号值的差值,通过计算ITAE(即函数适应度值)来判断是否满足算法的停止条件,若满足则计算过程结束,若不满足则循环操作,直到得到满足设定条件的数值或达到最大迭代次数。改进后的PID控制器见图3。
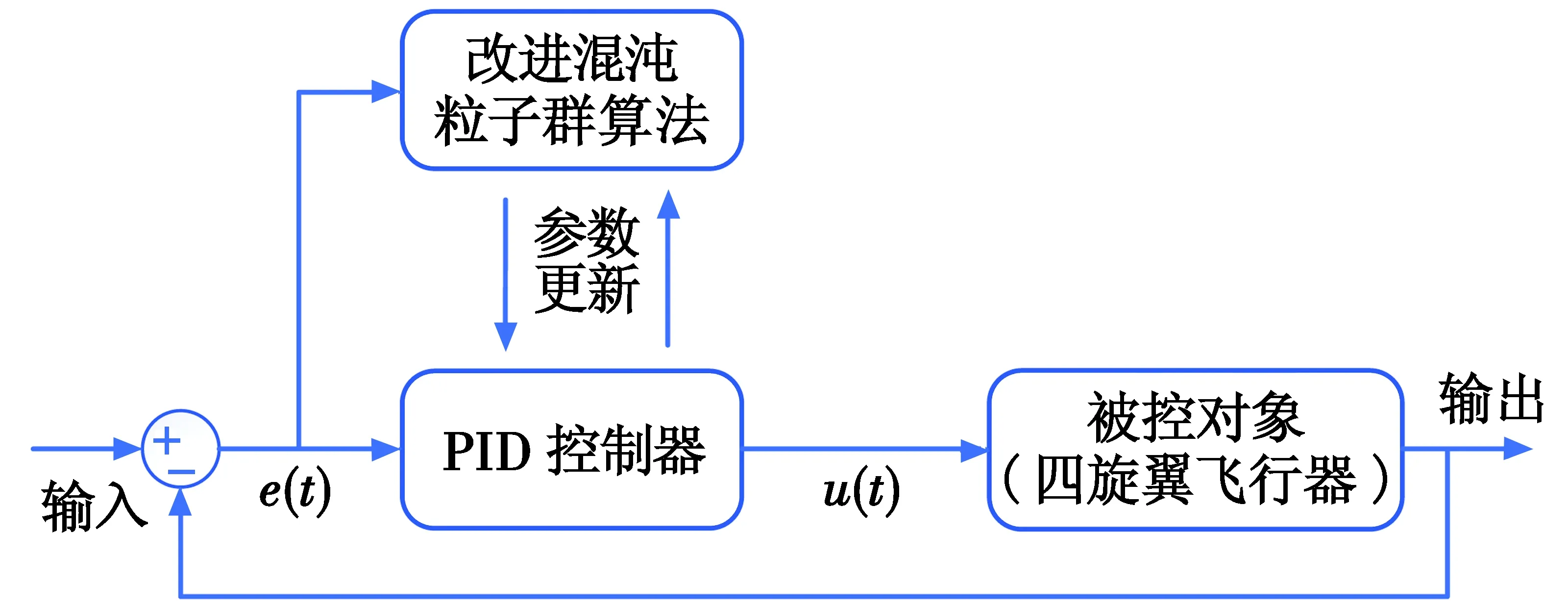
图3 改进混沌粒子群PID控制器Fig.3 Improved chaotic particle swarm PID controller
4 仿真实验
本文仿真实验选取四旋翼飞行器模型,仿真通道选取滚转通道和飞行高度通道。四旋翼飞行器参数和PSO算法初始化参数数据分别见表1和表2。

表1 四旋翼飞行器参数Table 1 Parameters of the quad-rotor flight controller

表2 PSO算法初始化数据Table 2 Initialized data of the PSO algorithm
本文采用PID控制器对四旋翼飞行器的姿态(翻转)和高度进行控制,在Matlab 2016b中搭建PID四旋翼数学模型。
仿真实验以滚转通道、高度通道为例,周期为0.01 s,滚转角度期望值为0.8 rad(约46°),飞行高度期望值为2 m。仿真结果分别如图4~7、表3~4所示。
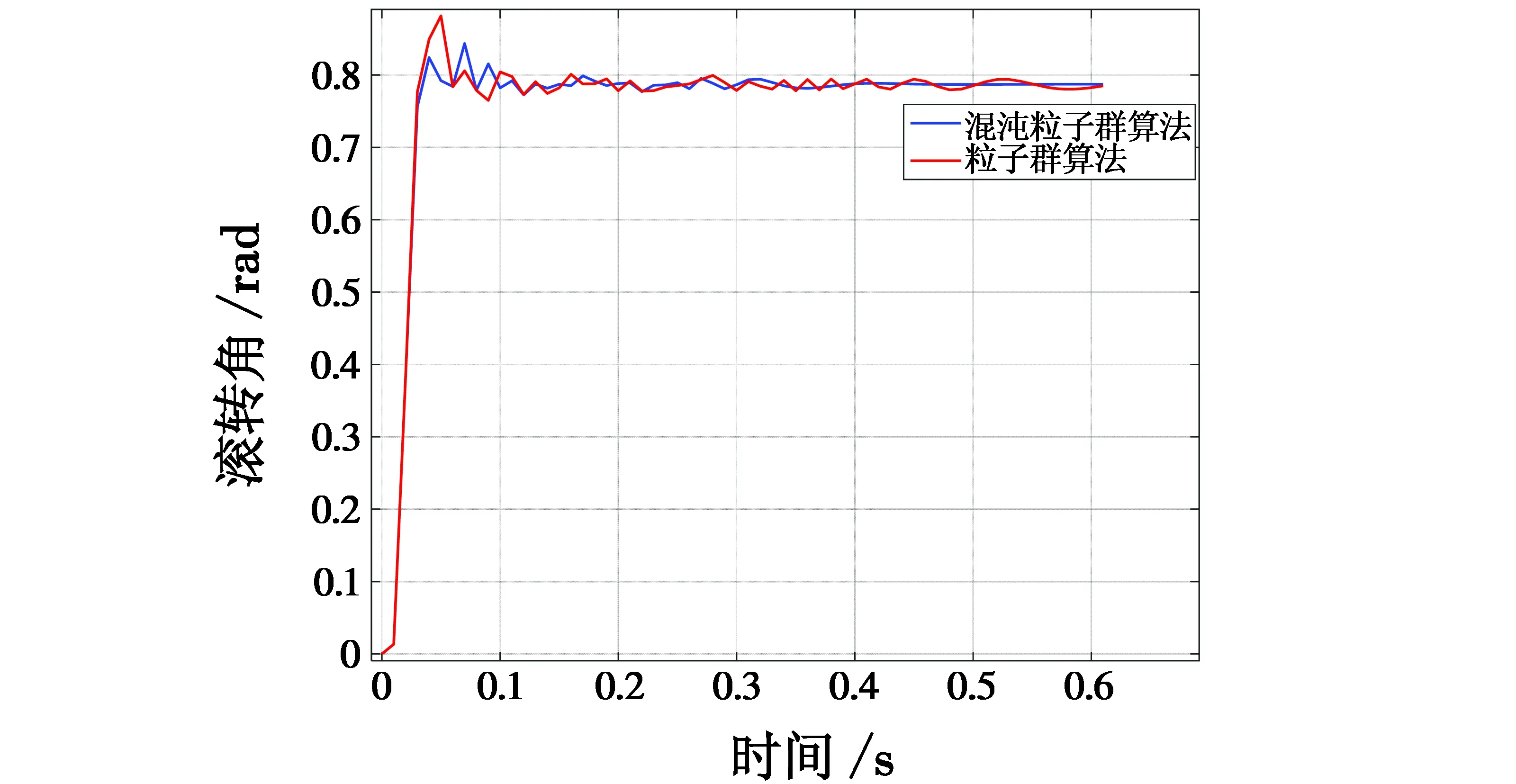
图4 四旋翼滚转角性能对比Fig.4 Performance comparison of quad-rotor roll angle

表3 滚转通道性能指标对比Table 3 Performance comparison of roll channel
从图4、图5和表3可以看出,在滚转通道的仿真实验中,本文算法控制器超调量明显小于标准粒子群算法的控制器,其次,调节时间更短,系统仿真验证了本文控制器的可靠性。
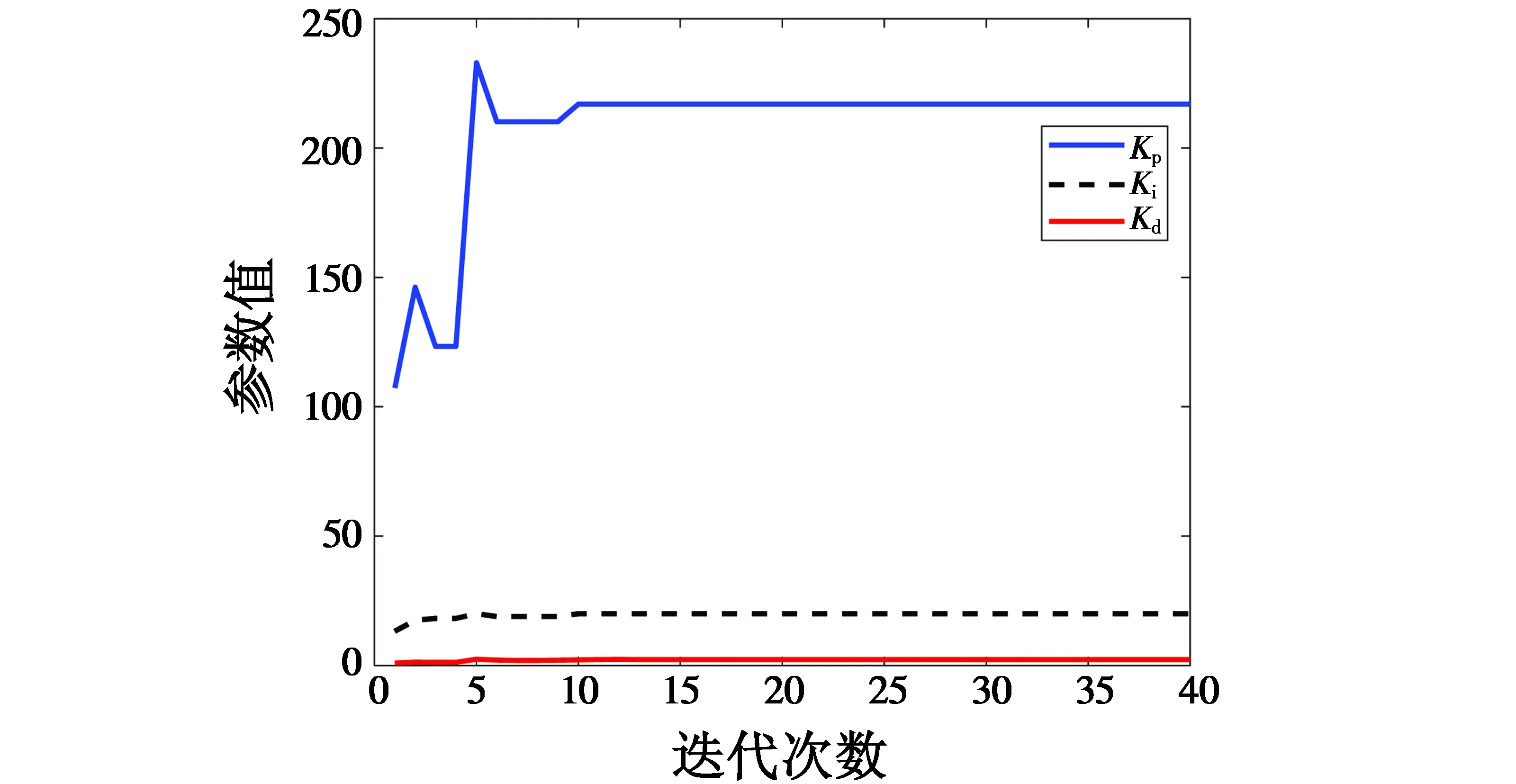
图5 改进后滚转通道PID参数趋势Fig.5 PID parameter trend of roll channel after improvement
从图5可以看出滚转通道PID参数Kp在第12次迭代后收敛,而Ki和Kd在第2次迭代后就已经收敛;从图7可以看出高度通道PID参数Kp和Kd在第20次迭代后收敛,而Ki在第4次迭代后就已经收敛,由此可以看出参数的调节时间大大缩短。
通过分析图6、图7和表4的仿真实验数据发现,本文算法下四旋翼无人机飞行高度波动和超调明显小于PSO算法,且调节时间更短,能够快速升至指定高度,具有良好的性能。

表4 飞行高度通道性能指标对比Table 4 Performance comparison of flight altitude channel
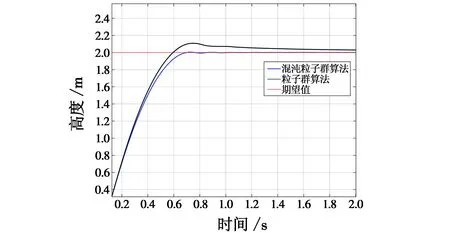
图6 四旋翼飞行高度性能对比Fig.6 Performance comparison of quad-rotor flight height
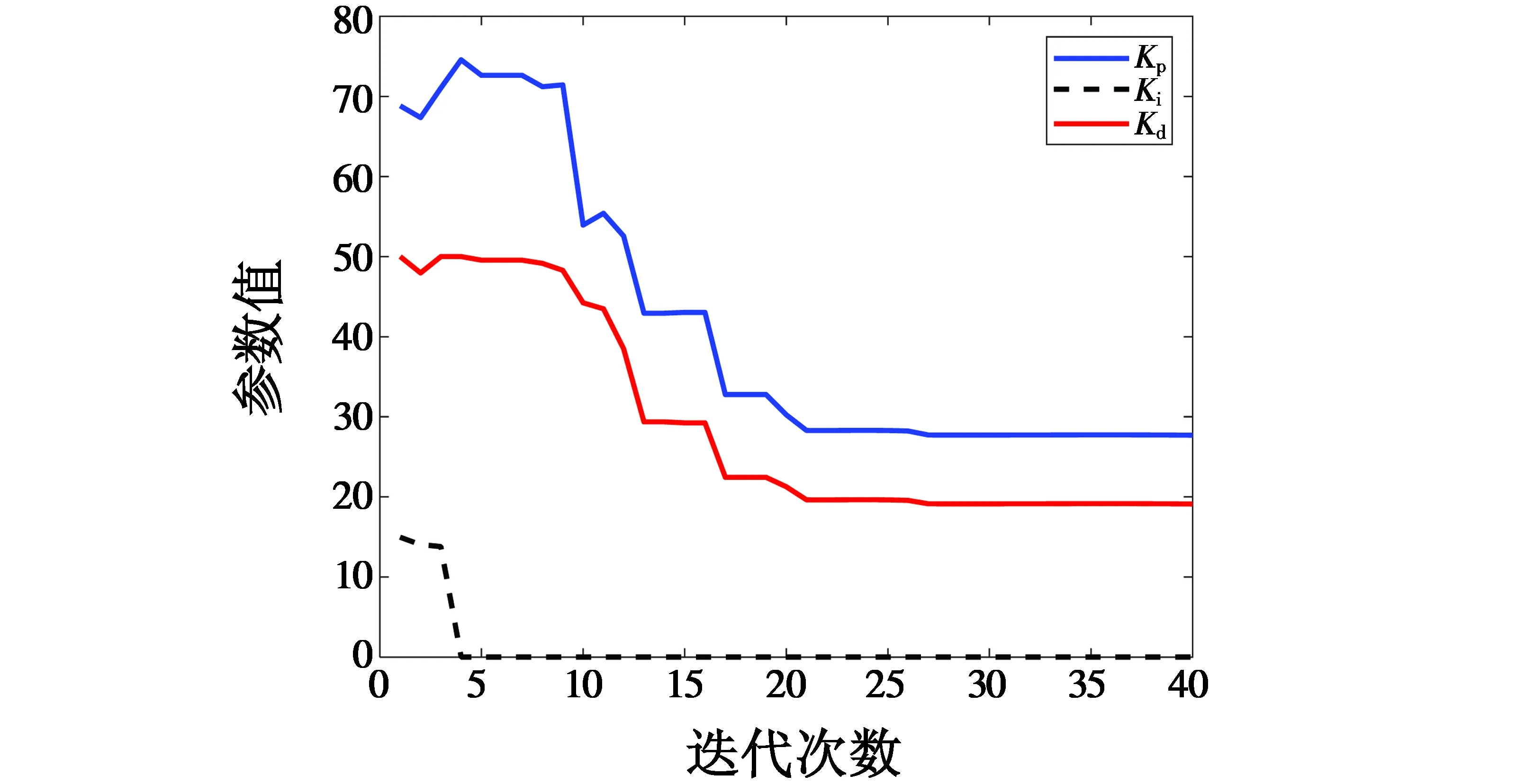
图7 改进后飞行高度通道PID参数趋势Fig.7 PID parameters trend of flight altitude channel
5 结论
针对四旋翼PID参数整定问题,本文在原有PSO算法基础上提出了结合Logistic混沌序列、自适应动态惯性权重的PSO算法。对四旋翼飞行器的飞行高度和飞行姿态进行控制,仿真得到的数据表明,本文算法在稳定性、最终解的质量和收敛速度等方面均优于标准PSO算法。
