考虑故障相关性的动车组多部件系统机会维护策略
2022-03-15王炳辉王红何勇刘晓阳
王炳辉,王红,何勇,刘晓阳
(兰州交通大学 机电工程学院,兰州 730070)
传统对动车组部件的预防性维护理论中,为了研究方便,对部件的可靠性评估均基于一个重要的假设-独立性假设,即系统中各部件之间相互独立,其故障率函数之间没有任何相互关联。而事实上,部件因为空间位置、结构设计、复杂环境及人为因素等使得系统中各部件的故障率具有一定的相关性。完全忽略这种相关性可能会对部件的可靠性评估造成误差,进而产生一定的经济损失,因此在动车组部件的维护过程中考虑部件故障之间的相关性是必要的。
Lai等[1]以两部件系统为研究对象,考虑部件之间的故障相关性,以维护成本率最小为目标,优化了系统的维护周期。葛阳等[2]针对“二态”单元和“三态”单元串联组成的两单元系统,考虑两个单元之间的故障相关性,建立了系统维修费用与维修间隔期的解析关系模型。文献[3-4]在为两部件系统制定预防性维修策略时,综合考虑故障相关和外部冲击两个方面的内容,优化了预防性维护周期内的可用度和费用率。张卓琦等[5]在故障相关的两部件系统中,采取年龄预防性维修与机会维修相结合的维修策略降低系统维修成本。以上文献以两部件系统为研究对象,对多部件故障相关系统的研究具有重要的参考意义。荣峰[6]将子系统之间的故障影响关系抽象成有向图模型,再利用pagerank算法对系统故障相关性进行分析。唐家银等[7]考虑了系统中各零部件工作寿命和故障部件修复时间之间的两类正相关性,将Copula相关理论引入到可修系统可靠性分析计算中,解决了可修系统故障相关可用度计算的建模问题,但是Copula函数法计算较为复杂,不能明确故障相关的作用方向及形式。王晓燕[8-9]基于大量故障数据,对复杂系统内部件之间的故障相关性进行分析,建立了故障链模型。文献[6-9] 是以多部件系统为对象,利用不同方法对部件之间的故障相关性进行研究,对其可靠性设计开展了工作,但未对维护修复非新条件下,设备可靠性及故障率的演化、设备维护周期的优化等问题进行深入研究。
机会维护是当部件在进行预防性维修或部件发生故障进行事后维修时,对满足预定条件的其他部件一起进行维护的方法。文献[10-12]采用机会维修策略,将预防性维修和故障维修有机结合起来,从而分摊系统的固定维修费用,实现了节约维修费用的目的;周晓军等[13-14]以多单元串行系统为研究对象,建立了一种基于设备可靠性的机会维护动态决策优化模型;侯文瑞等[15-16]提出基于可靠度阈值的机会维护模型,通过对系统运行历史数据的分析,设定预防性维护阈值和机会维护阈值, 对到达阈值的设备进行预防性维护,并同时对满足机会维护阈值的设备实施机会维护,得出最优维护成本;熊律等[17-18]针对高速铁路动车组引入机会维修里程窗的概念,对处于机会维修里程窗内关联部件的维修作业计划进行合并,从而降低动车组系统的停机维修次数。机会维护是一种考虑经济相关性的维护策略,其意义在于维护成本的节省。多部件故障相关系统中,部件故障率会由于部件之间的故障相关性而有所增加,因此通过机会维护策略整合维护资源,从而可以达到节约成本的目的。
本文考虑动车组系统内部件之间的故障相关性实际,利用故障链理论描述部件之间的故障相关性,对故障链模型中的双向故障相关问题进行研究,在维护修复非新条件下分析部件的可靠度及故障率的演化规律,进而优化部件的维护周期,并运用机会维护策略从系统层对部件的维护周期进行优化,以期在动车组维护作业中降低维护成本。
1 基本假设
以某型动车组四级修需要更换的某机械系统为研究对象,考虑部件之间的故障相关关系,在有限区间0~2.4×106km的运行里程内,优化部件的预防性维护周期。根据研究内容作出如下假设:
1) 部件从全新状态开始运行,即具有初始可靠度1;
2) 部件的固有故障率分布函数均服从威布尔分布;
3) 部件的维护方式是预防性维护、事后故障维护、保养、更换。事后故障维修只可以消除故障使部件恢复正常运行,并不能影响部件的可靠度衰减水平;保养伴随着动车组的整个运行,同样也不会影响部件的可靠度衰减水平;对部件的最后一次维护为更换;
4) 动车组每运行2×104km获得一次预防性维护的机会[19],所以部件的检修时机与整车的维护时机保持一致;
5) 动车组在运行过程中,系统内任一部件发生故障时或进行预防性维修时,整个系统需停机,机会维护只有在预防性维护停机时才进行。
2 预防性维护模型的建立
2.1 故障率模型的建立
2.1.1 固有故障率演化规则
周晓军[20-21]通过整合Malik[22]提出的役龄递减因子模型和Nakagawa[23]提出的故障率递增因子模型,建立预防性维护修复非新条件下的故障率演化模型,表达式为
λi+1(l)=biλi(l+aiLi)l∈(0,Li+1)
(1)
式中:λi+1(l)是第i次预防性维护后到i+1次间的固有故障率;ai为役龄递减因子,0
2.1.2 综合故障率分析
在故障链模型中,如果一个部件只主动影响其他部件,称为故障起点;如果一个部件既被动接受其他部件的影响,同时也在主动影响着其它部件,则称其为故障中点;如果只被动接受其他部件的影响,则称其为故障终点。当一个部件为故障起点时,它的综合故障率是它的固有故障率;当一个部件为故障中点或故障终点时,它的综合故障率不仅与自身的固有故障率有关,还受到其他部件的影响。如图1所示是两部件单向故障相关模型。

图1 两部件单向故障相关
单向故障链中部件B的综合故障率可借鉴文献[9]公式,即
λB(l)=λIB(l)+∑θBkλk(l)
(2)
式中:λB(l)为B部件的综合故障率;λIB(l)为B部件的固有故障率;θBk为k部件对B部件作用的相关系数;λk(l)为k部件的综合故障率。
对于双向故障相关模型,本质上是单向故障链模型的特殊形式,可根据故障链理论进行推导。图2所示是动车组中两个相互具有故障相关作用的部件。

图2 两部件双向故障相关
图2中,A和B都为故障中点,则当动车组运行到某里程l时,B和A的故障率公式分别为:
λB(l)=λIB(l)+θ1λA(l)
(3)
λA(l)=λIA(l)+θ2λB(l)
(4)
将式(4)代入式(3)得
λB(l)=λIB(l)+θ1[λIA(l)+θ2λB(l)]
(5)
进而可得B部件运行l里程时的故障率为

(6)
同理可得A部件运行l里程时的故障率为
(7)
式中:θ1为A对B作用的故障相关系数;θ2为B对A作用的故障相关系数。
2.1.3 维护非新条件下综合故障率的演化
以两部件单向故障相关为例说明维护修复非新条件下,部件之间的故障相关作用对被影响部件故障率及维修活动可能造成的影响。
根据式(2)可知,图1中B部件的综合故障率为自身固有故障率加上A部件对其的影响,则对A部件或B部件实施预防性维修后,B部件的综合故障率都应得到不同程度的降低。由此作出某段里程内B部件故障率变化的示意图如图3所示。

图3 两部件单向故障相关中被影响部件故障率变化曲线
图3中:lA,j和lA,j+1分别是A部件的第j次和第j+1次预防性维护时机;lB,j和lB,j+1分别是B部件的第j次和第j+1预防性维护时机。
2.2 单部件预防性维护成本建模
某k部件在(0,lmax)运行里程内,最后一次的维修活动为更换,对制定预防性维护周期没有影响,故在成本建模时不计更换成本。维护成本包括预防性维护成本、故障维护成本和停机成本。
C=Cp+Cr+Ct
(8)
(9)
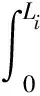
2.3 单部件预防性维护周期的确定
在(0,lmax)运行里程内,根据以可靠度为中心的维修理念[21],其表达式为

(10)
则由式(10)可知,给定预防性维护可靠度R,即可求出两次维护之间的间隔里程Li。由于动车组每运行2×104km才获得一次检修机会,而由式(10)得到的Li值可能并不是偶数,所以为了适应动车组的检修制度,还需对所得的Li值进行处理。本文对所得的Li值向下取整,若仍为奇数则再加1。此时部件的可靠度与给定的中心可靠度R值相比会有轻微的增加或减小。
通过最小化部件的维护成本即可得到部件最优中心可靠度R及R所对应的维护计划。
3 机会维护建模
在满足可靠度的前提下,设定机会维护里程窗Δl,如图4所示。当对A部件进行维护时,虽然B部件的预定维护时机尚未到达,但B部件的预定维护时机落在了机会维护里程窗内,可将B部件的维护时机适当提前与A部件一同维护,则可节约一次停机成本;由于C部件的维护时机没有落入机会维护里程窗中,故C部件不能参与此次的机会维护。
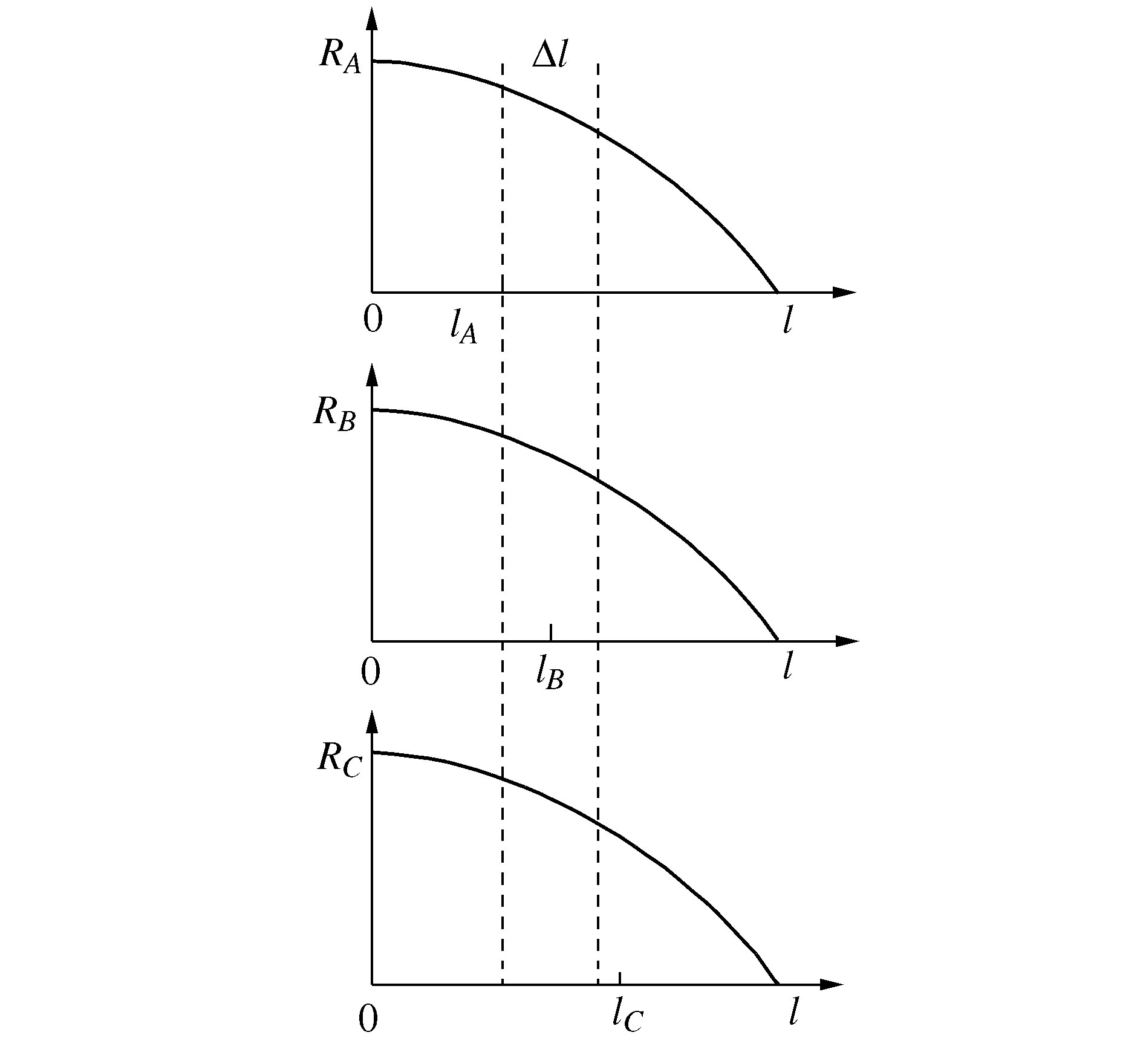
图4 机会维护示意图
所以在(0,lmax)运行里程内,系统层机会维护策略的实施步骤为:
1) 以可靠度为中心,以成本最小为目标,优化出各单部件的预防性维护周期;
2) 系统第u次维护时,将最靠前的单部件维护时机作为系统层机会维护时机,在机会维护里程窗中依次判断其他部件是否允许机会维护。接着再进入第u+1次维护,直至所有部件均完成维护。则机会维护的成本为
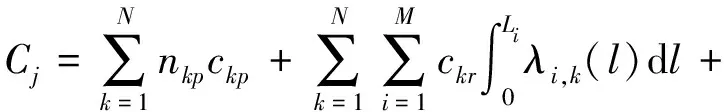
(11)
式中:nkp为k部件预防性维护次数;ckp为k部件的单次预防性维护成本;ckr为k部件的单次故障维护成本;ckt为k部件的单次停机成本;nkj为k部件的机会维护次数。
系统层部件的维护活动在该机会维护策略的调整下,部件两次维护之间的维护里程,相对于调整前会有一定的缩短或延长,从而相应的两次维护之间的故障次数也会减少或增加。当服役里程延长时部件的可靠度必然会比调整前降低。因此以每个区间的可靠度Rki≥Rkmin为约束条件,以Cj值最小为目标函数,即可得到最优机会维护里程窗Δl。
4 算例分析
以动车组某机械系统中的4个部件为例,其故障相关关系如图5所示。
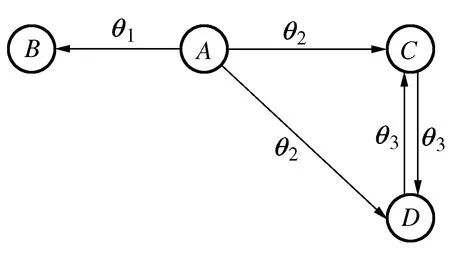
图5 系统内各部件的故障相关关系
由于威布尔分布对机械产品的寿命分布具有良好的拟合性质[20-21],故选用两参数威布尔分布函数描述这4个部件固有故障率随运行里程的变化,如式(12)所示。A、B、C、D这4个部件的最低可靠度分别不低于RA,min=0.70,RB,min=0.70,RC,min=0.78,RD,min=0.78。

(12)
式中:mk为k部件的形状参数;ηk为k部件的生命特征值参数。
两个调整因子分别取[21]:a1=a2=…=an=0.1,b1=b2=…=bn=1.1。根据2.1节所述有:
λia,A(l)=λia,IA(l)
(13)
λib,B(l)=λib,IB(l)+θ1λia,A(l)
(14)
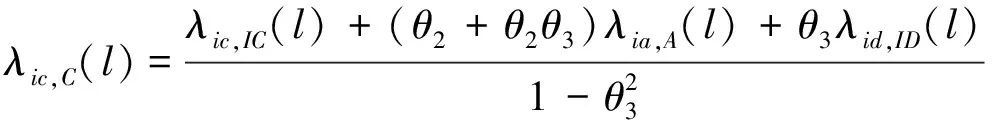
(15)
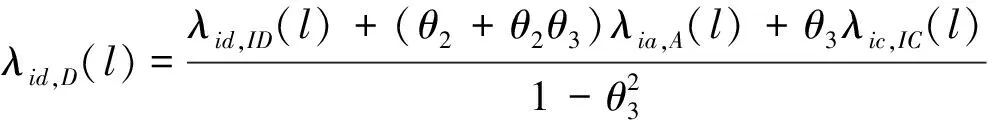
(16)
各部件的威布尔参数的取值借鉴文献[15,17],具体如表1所示。
由于非预期故障的发生不仅会导致系统停机,还可能造成更大生命财产的损失,具有较大的故障风险,因此故障维修成本应显著大于预防性维护成本,借鉴文献[17-18]确定其具体取值如表2 所示。各故障相关系数的取值借鉴文献[9]确定,具体如表4和表5所示。
根据2.3节所述,以可靠度为中心,最小化一个更换周期内的维护成本,优化得到A部件的维护计划如表3所示。
进而在不同的θ1取值下分析B部件的维护计划,通过在MATLAB中编程计算,分别得到不同θ1取值下B部件最优维护计划及成本对比如表4所示。
不同θ1取值下B部件C-R(成本-可靠度)曲线如图6所示,不同θ1取值下B部件可靠度变化曲线如图7所示。

图6 不同θ1取值下B部件的C-R曲线
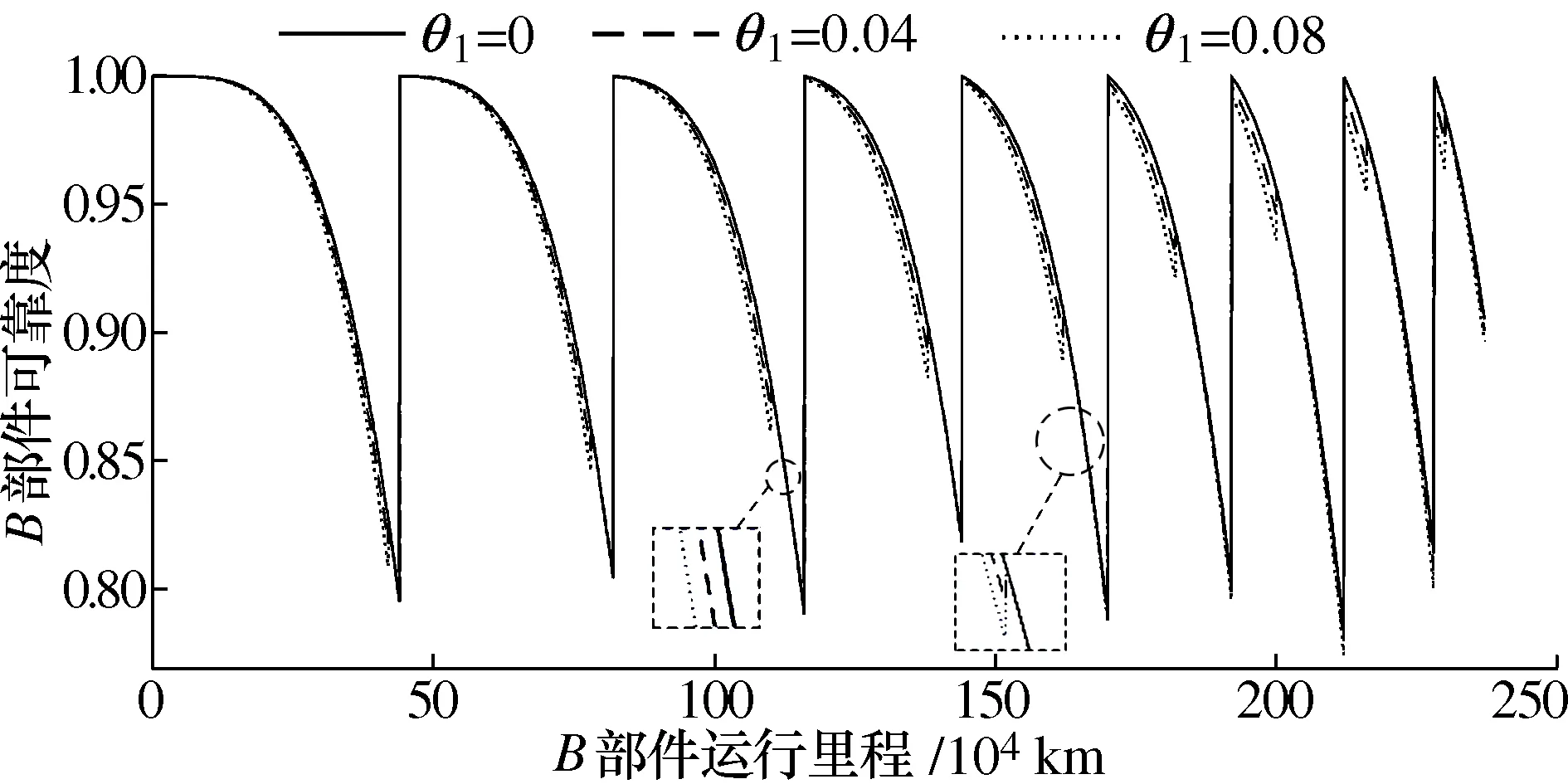
图7 不同θ1取值下B部件的可靠度曲线
由表4可知,当θ1=0时,B在可靠度为0.82时得到了最优的维护周期,此时成本为10 466.4 y;当θ1=0.04时,B在可靠度为0.81时得到了最优的维护周期,此时成本为10 797.1 y,二者相比,可靠度下降0.01且成本增加3.2%。当θ1=0.08时,B在可靠度为0.80时得到了最优的维护周期,成本为11 127.8 y,与θ1=0相比,可靠度下降0.02且成本增加6.3%。结合图6可知部件之间的故障相关作用越大,则为了保证部件的可靠度所花费的维护成本就越多。
由图7可知,同一运行里程时,θ1=0.04、θ1=0.08的可靠度小于θ1=0的值,同时θ1=0.08的可靠度小于θ1=0.04的值,说明部件受到的故障相关作用越大,则部件的可靠度就越小。图7中不同θ1取值下可靠度的大幅提升,是对B部件实施了预防性维护的效果。θ1取0.04、0.08时可靠度的小幅提升是对A部件实施了预防性维护的效果。当对A部件实施了预防性维护时,A部件的可靠度会得到极大的恢复,这时对B部件的影响就会相对减小,使得B部件的可靠度随着A部件的维护也得到一定程度的恢复。所以A部件的维护计划也在一定程度上通过影响B部件的可靠度而影响着B部件的维护计划。
由于部件C和部件D的威布尔分布函数的参数相同,所以属于同一类部件,可直接对二者使用成组维护策略,则其维护时机保持一致,得到维护计划如表5所示。

表5 部件C/D的优化结果
对系统层4个部件使用机会维护策略,在Δl=4时得到系统层最优维护计划,如表6所示。由表6可知,系统层采用机会维护策略之后系统的停机次数从21次减少到14次,预防性维护的总成本从42 570.8 y减少到38 110.5 y,节省10.5%。

表6 机会维修优化结果
5 结论
本文考虑系统内部件之间的故障相关性,在维护修复非新条件下分析了部件故障率的演化规律,实现了对部件可靠性的合理评估,进而优化了单部件的维护周期,并考虑部件维护的经济相关性,采用机会维护策略优化系统层部件维护的最优周期。由算例分析可知:
1) 当部件之间存在故障相关性时,若要保证被影响部件的可靠度,需要花费更多的维护成本;被影响部件的维护计划受到对它产生故障相关作用部件的维护计划的影响。
2) 对系统层4个部件使用机会维护策略使系统总维护成本降低了10.5%,随着我国早期投入运营的动车组大量进入高等级维护周期,研究结果对动车组设备的维护决策有较好的经济意义。
