约束型粒子群的LCC/S磁谐振耦合机构参数优化算法

吴晓伟，刘宏昭

(西安理工大学 机械与精密仪器工程学院,西安 710048)

机电一体化技术是将机械、电子、微电子、信息、传感器等进行有机结合的综合技术。将传感器技术应用到机械系统中,能够更好帮助机械系统朝着创新方向发展[1-3]。然而对于不同部件相对运动的机械设备,传感器供电多采用接触式,该方式存在导电体裸露等安全隐患的同时也会给相对运动造成阻碍。无线电能传输(Wireless power transfer, WPT)技术[4]能有效克服接触式电能传输存在的弊端。在固定式充电和动态式充电中均发挥着重要作用,如电动汽车[5-6]、旋转超声领域[7]、多自由度电机[8]等。由于WPT系统的磁耦合机构中发射与接收线圈之间存在一定的距离使得线圈间耦合系数降低,从而导致系统能量传输效率不高,需要对系统设计相应的谐振补偿拓扑,以提高能量的传输效率[9-10]。传统低阶谐振补偿拓扑虽易于计算,但是高阶谐振补偿拓扑具有更好的输出特性,因此LCL[11]、LLC[12]、CLC[13]以及LCC[14]等高阶谐振补偿拓扑被提出。对谐振补偿拓扑的参数分析,多是针对输出功率或效率进行单一目标优化设计。而高阶谐振补偿拓扑参数之间具有非线性,强耦合特性,使得系统在输出功率与输出效率呈现出非线性特性。因此,如何提高效率的同时获得满足负载所需功率受到关注,文献[15]提出了一种最大能效积指标对谐振补偿拓扑进行优化的方法,可以同时兼顾系统效率与输出功率,但该方法是基于低阶谐振补偿拓扑进行优化,对于高阶LCC/S型谐振拓扑会出现模型构建困难,方程极值求解困难等问题。

对于不同部件相对运动监测型传感器的供电问题,其工作示意如图1所示。

多类别传感器的使用与相对运动的特性必然会导致WPT系统负载与磁耦合机构中收发线圈位置发生变化,从而影响系统整体效率和功率输出。考虑到低阶谐振补偿拓扑易受负载与耦合系数影响,导致系统谐振频率发生漂移,从而出现系统工作不稳定的问题,监测型传感器无线供电系统的磁耦合机构采用LCC/S型高阶谐振补偿拓扑。考虑到现有监测传感器的供电功率多在2 W～20 W之间,本文将通过建立约束条件并结合粒子群算法(Particle swarm optimization, PSO)形成约束型粒子群算法(Constrained particle swarm optimization, CPSO),对LCC/S磁耦合机构的参数进行寻优,使得线圈半径小于5 cm的磁耦合机构满足如下指标:30 Ω负载移动范围内接收端输出功率为5～15 W,传输效率大于50%。

1 LCC/S磁耦合机构分析

如图2所示,LCC/S型WPT系统由全桥高频逆变器Ⅰ、LCC/S磁耦合机构Ⅱ和整流滤波电路Ⅲ这3部分组成。

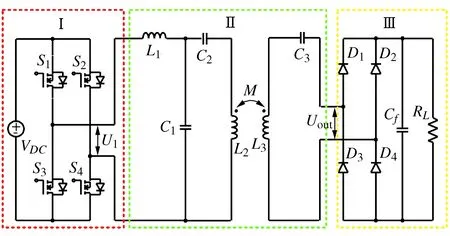
图2 LCC/S型WPT系统

1.1 LCC/S型磁耦合机构数学模型

为了研究耦合线圈偏移对磁耦合机构传输效率的影响,分析能量收发圈轴心距离d与横向距离h变化对线圈间互感的影响。两单匝线圈的位置关系如图3所示,其中r1与r2分别为两线圈的半径。

图3 线圈相对位置

由诺伊曼公式可得不同位置时两线圈间互感系数为

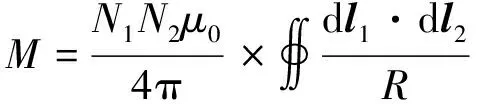
(1)

经计算可得积分元dl1、dl2和距离R的表达式如下:

dl1=r1(-xsinα+ycosα)dα

(2)

dl2=r2(-xsinβ+ycosβ)dβ

(3)

2r1r2(cosαcosβ+sinαsinβ)]1/2

(4)

将式(2)～式(4)代入式(1)中,得到互感Mij的表达式为

进而可得平面圆形螺旋线圈之间互感系数ML为

(6)

式中：n1和n2均为线圈匝数。

由式(6)可知当监测传感器位置发生变化时,磁耦合机构的线圈互感系数与距离成反比关系。

图4为LCC/S磁耦合机构等效原理图,其中机构接收端阻抗为

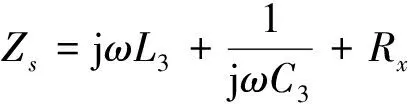
(7)

其中,图2整流滤波电路与负载RL可等效为Rx,且Rx=8RL/π2。

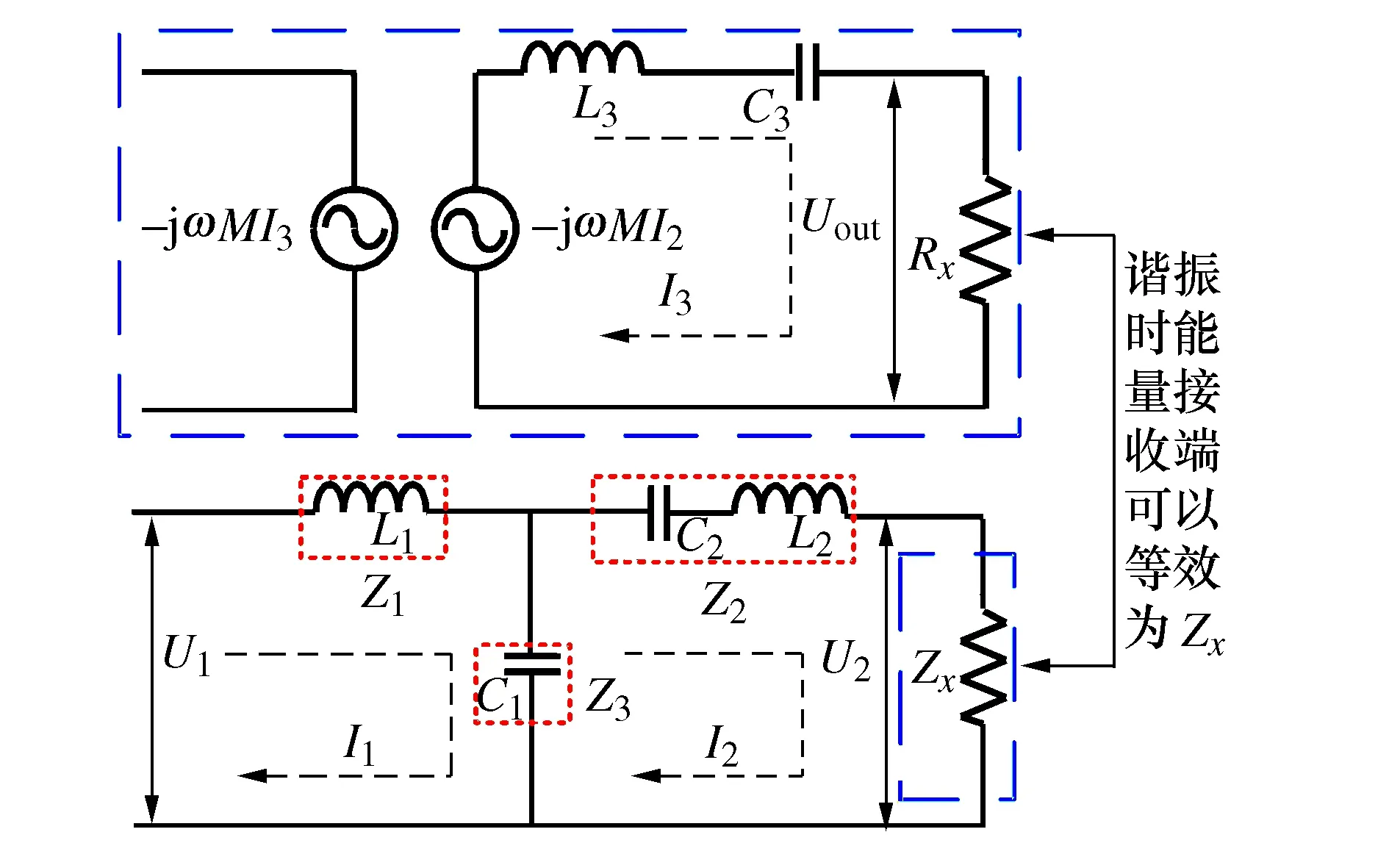
图4 LCC/S磁耦合机构等效模型

LCC/S磁耦合机构工作在谐振状态时接收端在发射端的反射阻抗为

(8)

根据基尔霍夫电压定律可得：

(9)

发射线圈中的电流I2为

(10)

其中：

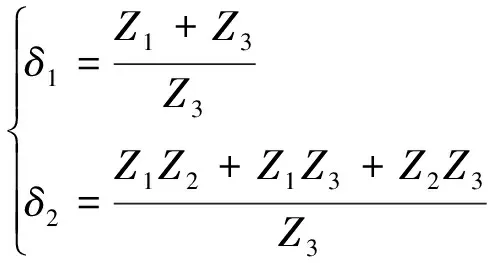
(11)

分析式(10)可知,当谐振参数Z1～Z3确定后,磁耦合机构接收端等效阻抗Zx为唯一变量,若需发射线圈中的电流保持恒定,仅需δ1=0。由此得出发射线圈电流恒定的条件为

(12)

同时由图4可知系统的输入阻抗为

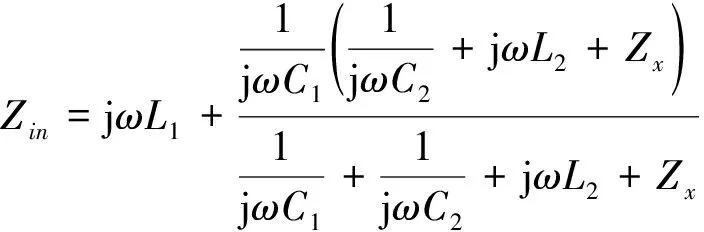
(13)

根据基尔霍夫电流定律,可知各支路电流值为：

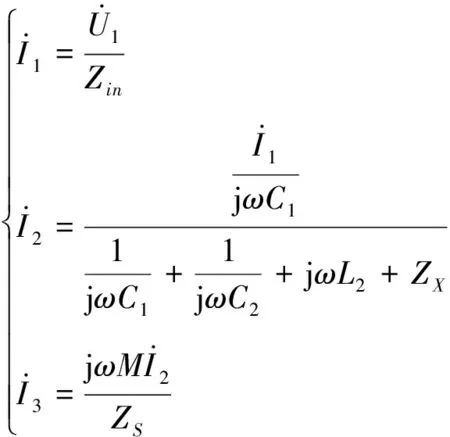
(14)

由此可得LCC/S型WPT系统输入功率Pin、输出功率Pout以及传输效率η分别为:

(15)

1.2 LCC/S磁耦合机构输出特性分析

分析LCC/S磁耦合机构相关参数对系统输出的影响,对其进行数值仿真,参数如表1所示。

表1 LCC/S谐振补偿参数

将表1所示参数代入式(13)进行数值仿真。负载Rx=50 Ω,耦合系数k分别为0.01、0.1和0.2时,在40～120 kHz工作频率范围内磁耦合机构输入阻抗角变化曲线如图5所示。

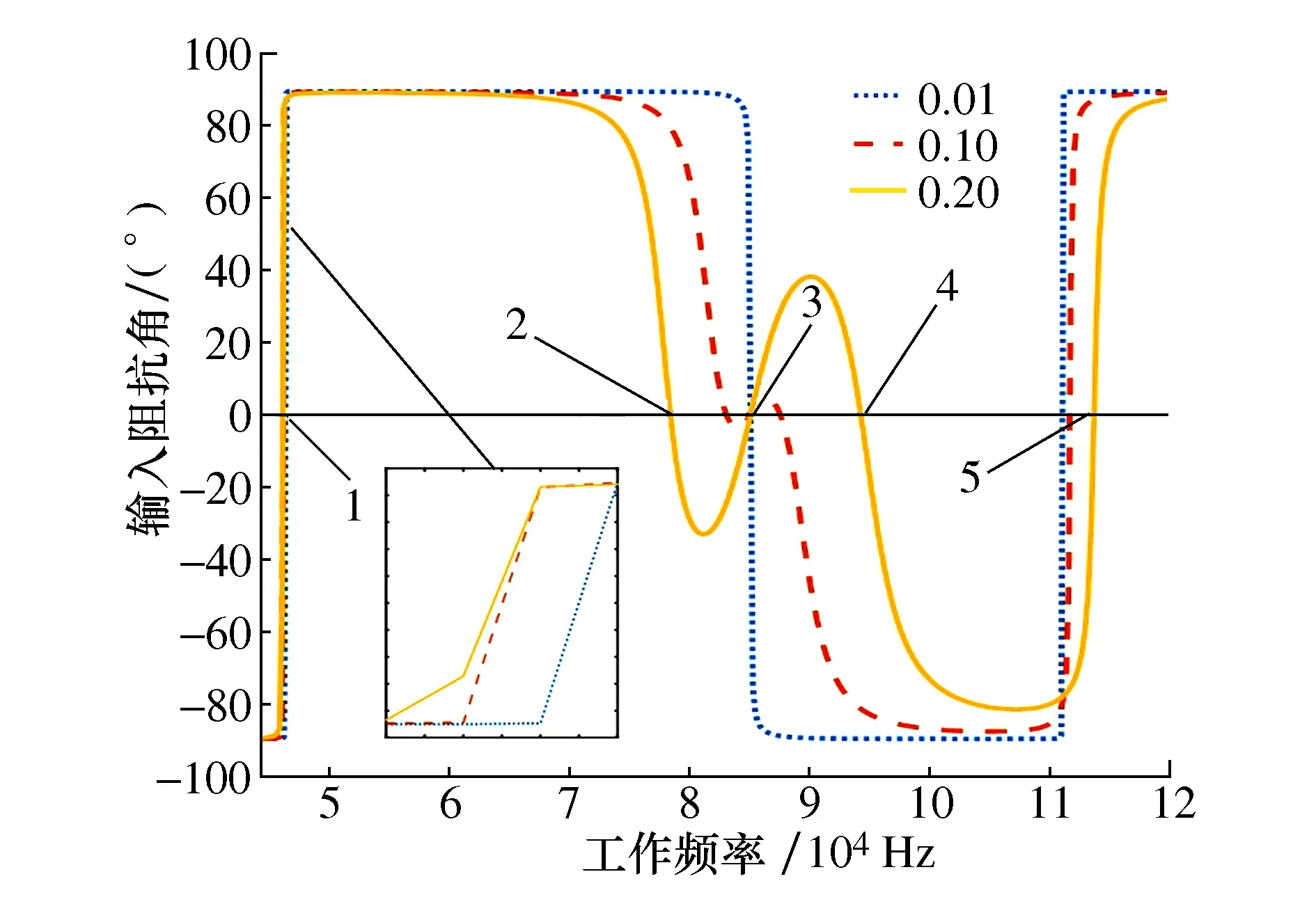
图5 Rx=50 Ω机构输入阻抗

耦合系数k=0.1,负载分别为10 Ω、100 Ω、1000 Ω磁耦合机构输入阻抗角的变化曲线如图6所示。

图6 k=0.1机构输入阻抗

从图5和图6可以发现曲线与零相角有5个交点,对应着5种工作模式。其中,工作模式2、4和5及易受负载和耦合系数影响,稳定性极差不具有实际应用意义;工作模式3不受负载和耦合条件变化的影响,此时系统的开关工作频率与发射侧固有谐振频率以及接收侧固有谐振频率相等;工作模式1受负载和耦合系数的轻微影响,易发生频率漂移。

考虑到安装在运动部件上的监测型传感器会发生相对位移且可适用的传感器型号繁杂,从而导致磁耦合机构的耦合系数与负载易发生变化,所以工作模式3最适合运动监测型传感器的工作状态。因此结合式(7)～式(13),可得LCC/S型磁耦合机构在工作模式3,即全系统谐振的条件为:

(16)

耦合系数k=0.1，负载为50 Ω时,依据式(15)对系统的输出特性进行数值仿真,结果如图7所示。

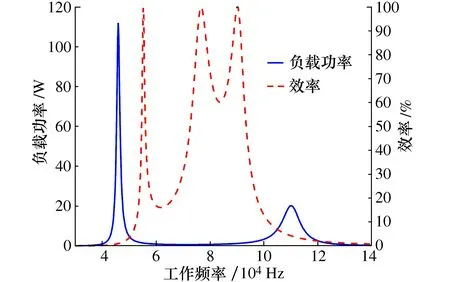
图7 RL=50 Ω机构输出能效

由图7可知,LCC/S磁耦合机构最佳输出效率与最高输出功率的频率工作点存在不匹配现象,即在系统的最佳输出效率工作点处,可能存在着负载输出功率不足的问题。

综上所述,当LCC/S磁耦合机构的耦合系数或负载发生变化时工作模式3具有稳定的输出特性,适合运动监测型传感器的工作环境。但此时系统最佳输出效率与最高输出功率的频率工作点不一致。

2 磁耦合机构参数优化

由于LCC/S磁耦合机构参数之间具有非线性,强耦合特性,导致该机构在输出较高效率的同时难以提供满足负载所需的功率。为使其具有良好的输出特性,本节将结合输出效率、能量传输特性和负载所需功率构造约束条件,然后通过PSO算法对该模型进行寻优求解。

2.1 构建约束型优化模型

当LCC/S磁耦合机构的工作状态满足式(16)时,WPT系统可以工作在模式3的谐振状态。建立优化模型过程如下:

步骤1 确定磁耦合机构能量耦合线圈相关参数。根据传感器体积设计能量耦合线圈,计算线圈自感以及线圈间耦合系数。

步骤2 确定目标函数与约束条件。以LCC/S磁耦合机构的最佳输出效率为目标函数,以负载所需功率及工作模式为约束条件。结合式(15)和式(16)构造约束型优化模型。

(17)

步骤3 约束型优化模型去约束化。引入罚函数将式(17)转化为求解无约束函数的极大值问题,由此构造具有惩罚项的多变量目标函数，即

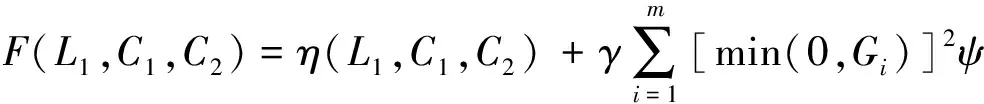
(18)

式中：罚因子γ=1015;ψ为约束判断条件,其值在满足约束时为0,否则为1。

2.2 粒子群参数优化

CPSO算法对LCC/S磁耦合机构参数优化过程如图8所示。其中,输入电压u和工作频率f根据实际应用确定,耦合系数k根据磁耦合机构发射线圈与接收线圈之间距离确定,等效负载Rx由实际应用对象决定。

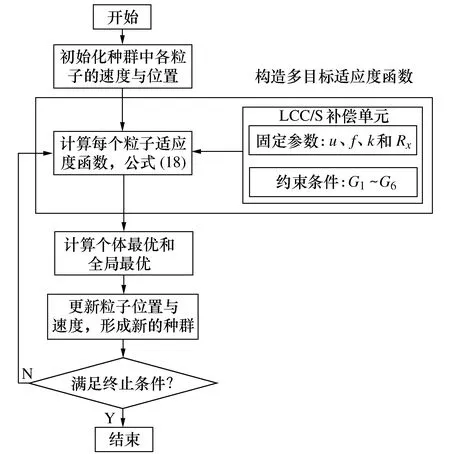
图8 优化算法流程

基于粒子群算法优化多变量目标函数的步骤如下:

步骤1 对种群中各粒子的速度和位置进行初始化设置。

步骤2 对每个粒子的适应度函数式(18)进行求解。计算过程中,判断当前粒子位置是否满足约束条件,当满足约束条件时,ψ=0;不满足约束条件时,ψ=1。储存每个粒子的最佳位置和适应度,并从种群中选择最好的粒子位置作为种群的全局最优位置。

步骤3 更新粒子的速度与位置,产生新的种群。

步骤4 对新的种群中每个粒子的适应度进行求解,将该适应度与之前最好位置所对应的适应度对比,如果更好,则将其当前的位置作为该粒子的最好位置。

步骤5 将每个粒子的适应度与全体粒子所经历的最好位置比较,如果更好,则对位置的值进行更新。

步骤6 若没有达到预设条件,则返回步骤3;当达到最大次数或满足适应值,则停止迭代,输出最优解。

3 仿真验证

为了验证CPSO优化算法的有效性,设计了如图9所示的磁谐振耦合机构能量收发线圈。基于有限元分析可得两相同尺寸螺线圈的自感均为5.857 34 μH。两线圈最近距离工作点如图9a)所示,互感为1.689 79 μH;图9c)为两线圈最远距离工作点,互感为0.527 55 μH。

图9 线圈尺寸及相对位置

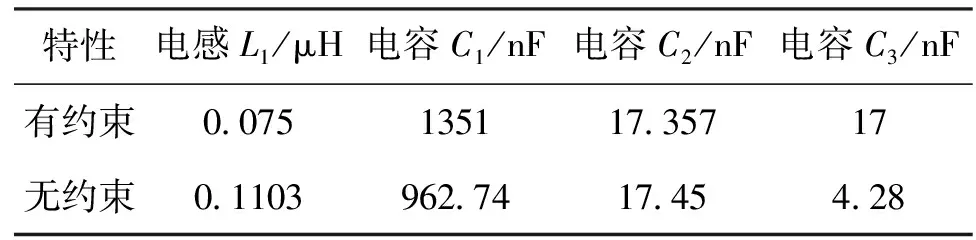
表2 LCC/S磁耦合机构优化参数

为了方便对比分析,本文以无约束PSO算法与有约束PSO算法分别对磁耦合机构相关参数进行了寻优求解,所得参数如表2所示。依据表2参数在PSIM软件中搭建了LCC/S型磁耦合机构仿真电路,其中电源内阻为1 Ω。当线圈位置发生变化时,线圈间的互感随之发生变化,两组参数输出能效曲线如图10所示。

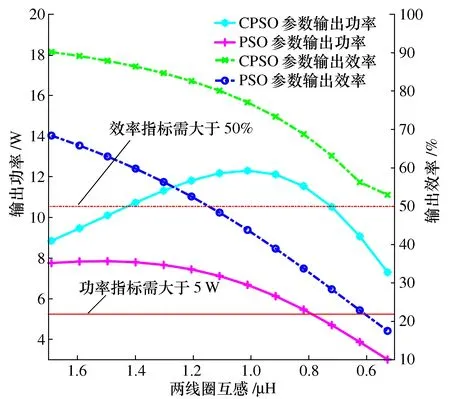
图10 输出能效曲线

通过图10可知：基于CPSO寻优参数的磁耦合机构在线圈活动范围内的输出功率与输出效率均符合设计指标;而基于PSO寻优参数的机构在两线圈互感低于1.109 μH时传输效率无法够满足性能指标。此外,CPSO优化参数在如图9a)所示线圈位置的输出功率为8.854 026 1 W,输出效率达到90.18%;两线圈互感为1.206 μH位置处的输出功率为11.823 W,此时输出效率只有82.61%;由此再次证明了LCC/S磁耦合机构存在最佳输出功率与最高输出效率工作点不一致的问题。最后,对比图中曲线可以发现CPSO优化参数的磁耦合机构在有效范围内输出功率与输出效率均更具优势,其参数在提高效率的同时,可以提供满足负载所需的功率,且算法所得参数可以满足约束条件G1～G2。

对于CPSO优化算法的磁耦合机构输出特性更具优势的问题,以PSIM软件仿真得到CPSO算法与PSO算法的机构输入状态如图11与图12所示。其中,图11a)和图12a)的线圈互感为1.689 79 μH,搭载30 Ω负载,图11b)和图12b)线圈互感0.527 55 μH,负载3 Ω。可以发现CPSO算法,在线圈位置与负载发生变化后机构的输入电压与输入电流相位基本保持一致。对图11b)中A点放大可以发现电压与电流相位仅存在极小偏差,这是由于仿真迭代精度所造成。由此可知,此时机构工作在全系谐振模式下,CPSO优化所得参数满足算法约束条件G3～G6。对于图12,在线圈位置与负载发生变化后,机构输入电压与电流间存在较大的相位差,这是由于PSO优化缺乏与磁耦合机构相关约束条件,使得机构无法工作在全系统谐振模式,此时机构输入阻抗易受互感和负载影响。

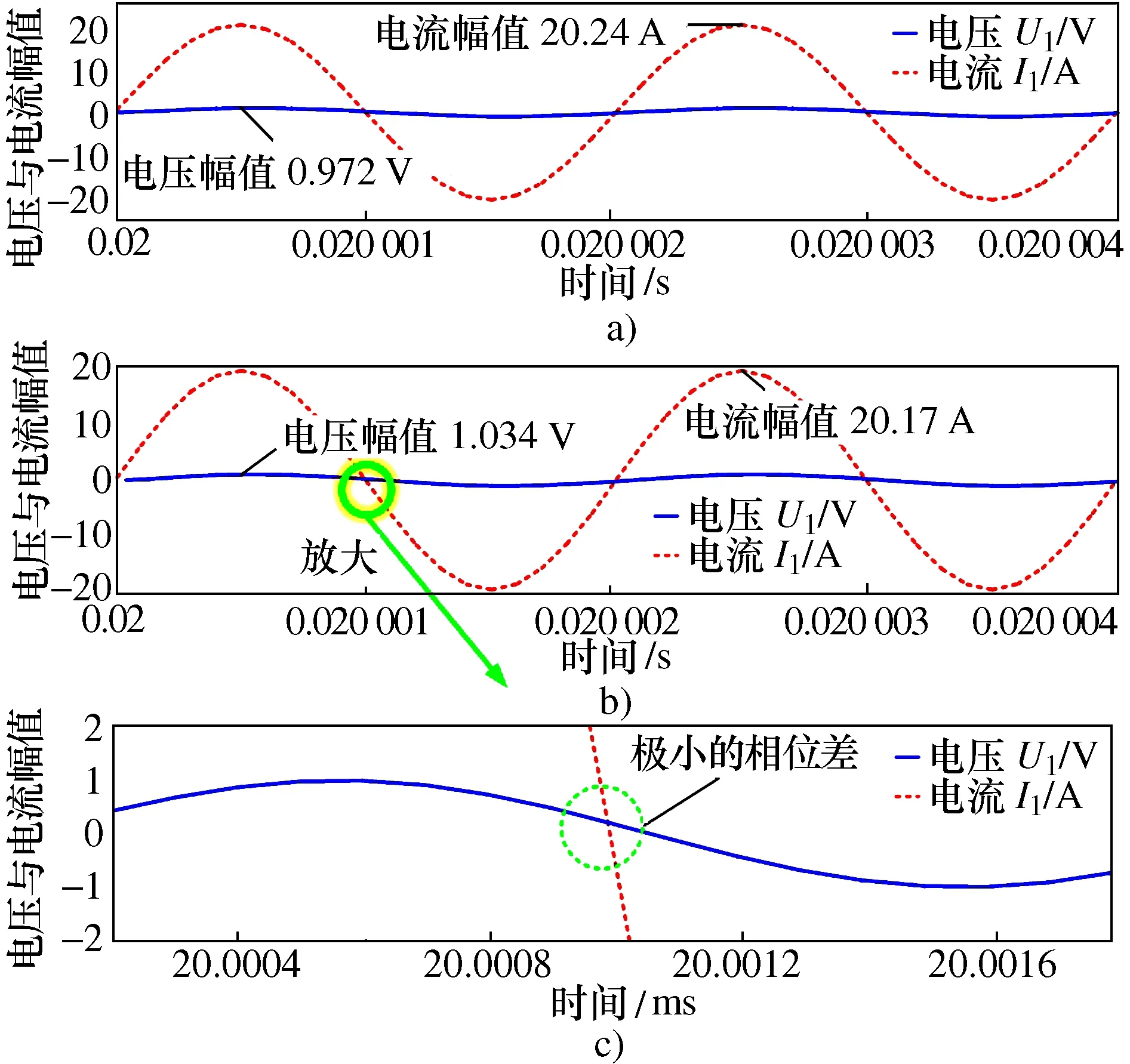
图11 CPSO参数仿真

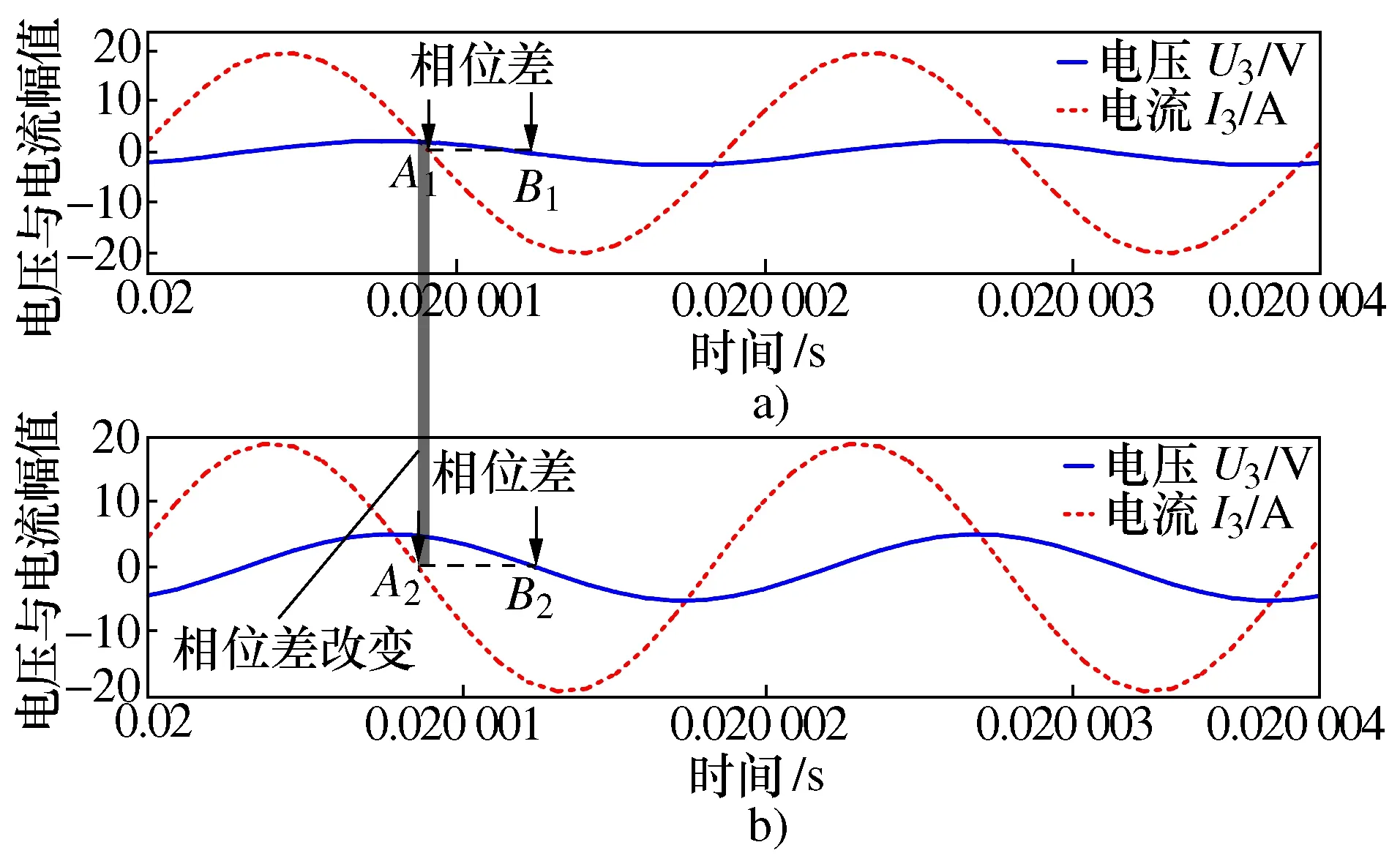
图12 PSO参数仿真

为了进一步证明约束条件在能量传递过程中的重要性,参照图9所示线圈位置,对CPSO与PSO优化的LCC/S磁耦合机构进行有限元仿真,结果如图13所示。

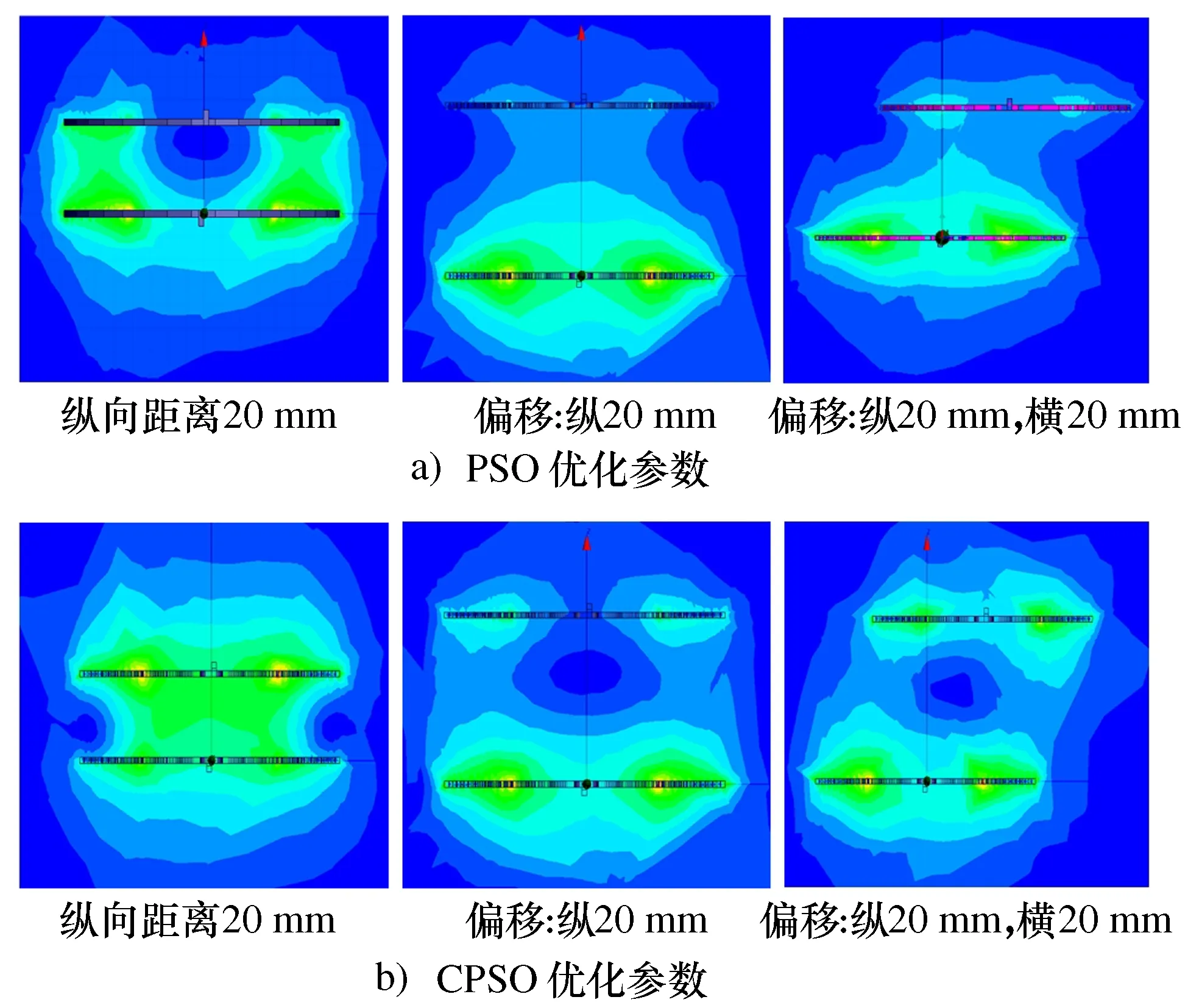
图13 线圈能量耦合示意

从图13中可以发现,CPSO优化算法机构的能量耦合程度明显高于PSO优化算法。

综上所述,相对于PSO优化算法,基于约束条件G1～G6的CPSO优化算法更具优势。CPSO优化算法所得参数可以使得LCC/S磁耦合机构在互感和负载发生变化时,依旧保持该机构工作在谐振模式,且输出能效可以满足设计指标。

4 结论

分析了机械系统中监测型传感器无线供电问题,通过对LCC/S磁耦合机构建模,分析了该型磁耦合机构在不同耦合系数与不同负载影响时的输出特性。发现该机构具有五种不同的工作模式,确定了适合运动监测型传感器的工作模式。依据运动监测型传感器的工作指标与工作特性构建了约束型优化模型,并通过引入罚函数将约束问题去约束化,结合粒子群算法对去约束化模型求解。最后通过仿真验证了本文约束型粒子群优化算法的可行性,结果表明该算法所得优化参数可以使机构在获得较高效率的同时为其提供满足性能指标的功率。