数控机床进给系统时变特性建模与分析

姚亚健，张铮

(湖北工业大学 机械工程学院,武汉 430068)

数控机床是一个复杂的机电系统,其工作性能、加工精度与加工效率取决于机床的结构设计、静动态特性、数控算法、控制系统和加工工艺系统等诸多方面[1-2]。

目前机床线性进给系统静态误差建模、检测、辨识和补偿的理论研究[3-7]已经相对成熟,文献[3]对整机精度设计指标的确定,进一步缩小了机床与试件相对位姿误差的范围。文献[4-5]针对空间误差进行精确建模,采用智能算法对其进行优化补偿。文献[6]提出了一种基于球杆仪的五次安装测量辨识运动误差的方法。文献[7]针对特定的误差模型进行系统性的误差补偿测试。然而对于伺服动态误差的研究仍然还停留在初级阶段[8-12]。

大量研究表明,影响机床的伺服动态误差的因素不仅包括控制系统伺服增益,还包括进给单元的位置、速度和加速度等运动参数,伺服动态误差是控制系统和机械系统耦合作用的结果。Andolfatto[13]等认为机床的伺服动态误差是机床速度、加速度和进给速度等变化产生的动态力作用,导致的机床机械系统产生弹性变形误差。王磊等[14]考虑多轴联动机床的运动过程中,机床加减速将会导致机床结合部刚度非线性变化,从而导致系统动态特性改变,其采用集中参数法建立了一台三轴数控机床动力学模型,然后运用有限元方法分析了位置变化下的系统响应变换。李杰等[15]考虑进给机构的集中柔性和分布柔性,建立了机电-刚柔耦合的动力学模型,分析了进给系统动态误差的产生过程以及各类因素的对动态误差的影响规律。

在文献[13-15]中,其传统的伺服动态误差建模方法中为获得的系统刚度,阻尼等参数主要是运用动力学参数辨识法在静态的情况下获取,当进给系统单元位置、速度和加速等运动参数变化时系统的刚度,阻尼等参数也会随之变化[14,16-18],那么传统的仅考虑静态情况下的伺服动态误差建模将不再适用于高速运动中的机床。同时,进给速度加至一定高速(10 000 mm/min)范围,伺服误差在总误差的比重超过75%[19]。因此为准确的建立机床高速运动中的伺服动态误差模型,需要建立一种基于时变特性的进给系统伺服动态误差模型,为机床进给轴伺服动态误差的补偿打下基础。

本文采用集中参数法和控制理论建立了考虑进给系统刚度值、阻尼值随速度、加速度变化的时变特性伺服系统模型,通过给定正弦输入信号,利用MATLAB中Simulink模块仿真得到了时变特性下的进给轴输出值,并与传统伺服系统的输出值进行了对比分析。最后以本实验室THC6350IV双转台卧式加工中心进给系统为例,进行了球杆仪实验验证。

1 含时变特性的进给机构动力学建模

1.1 机床进给机构物理模型的等效

数控机床控制系统的跟随误差和机械系统的弹性变形误差,将会导致数控机床进给系统输入指令与输出不匹配,即伺服动态误差。当进给系统的整体柔性、刚度变化其固有频率和惯性也随之变化,因此建立精确的机械和控制系统模型是准确分析伺服动态误差的关键。

典型的数控机床单轴进给系统结构如图1所示。其主要由床身、工作台、滚珠丝杠副、导轨滑块副、电机、联轴器、支撑轴承轴承等部件构成。采用集中参数法建立其动力学模型,如图2所示。

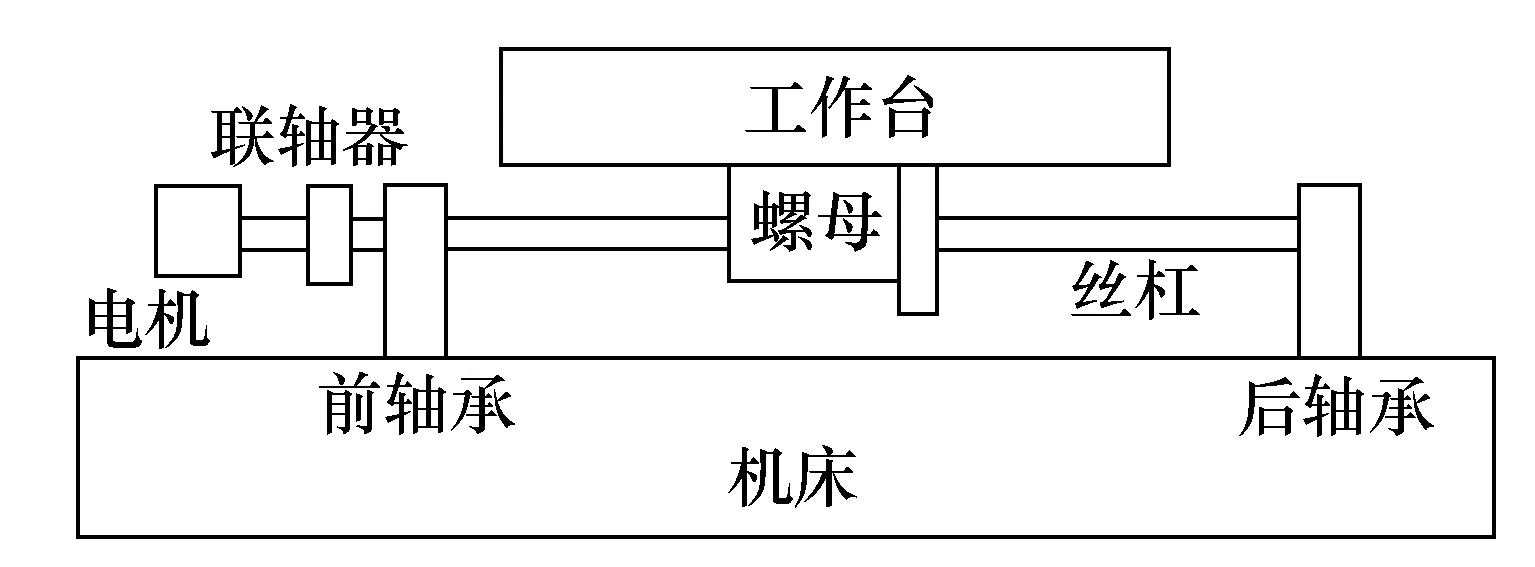
图1 进给系统结构图

图2 进给系统动力学模型

根据牛顿第二定律,数控机床进给系统的动力学方程为:

(1)

式中:Mt为工作台质量;Jm为电机与联轴器的等效转动惯量;Jl为滚珠丝杆的转动惯量;θm为伺服电机的转角;θl为滚珠丝杠的转角;Xl为滚珠丝杠的轴向位移;Xt为工作台的轴向位移;Cl为滚珠丝杆阻尼系数;Ct为导轨的阻尼系数;l为滚珠丝杠导程;η为丝杠螺母副的传动效率;Kθ为联轴器与滚珠丝杠的等效转动刚度;Ke为伺服系统等效轴向刚度。

将式(1)进行拉普拉斯变换,与一典型控制系统相结合得到机电耦合的进给系统如图3所示。

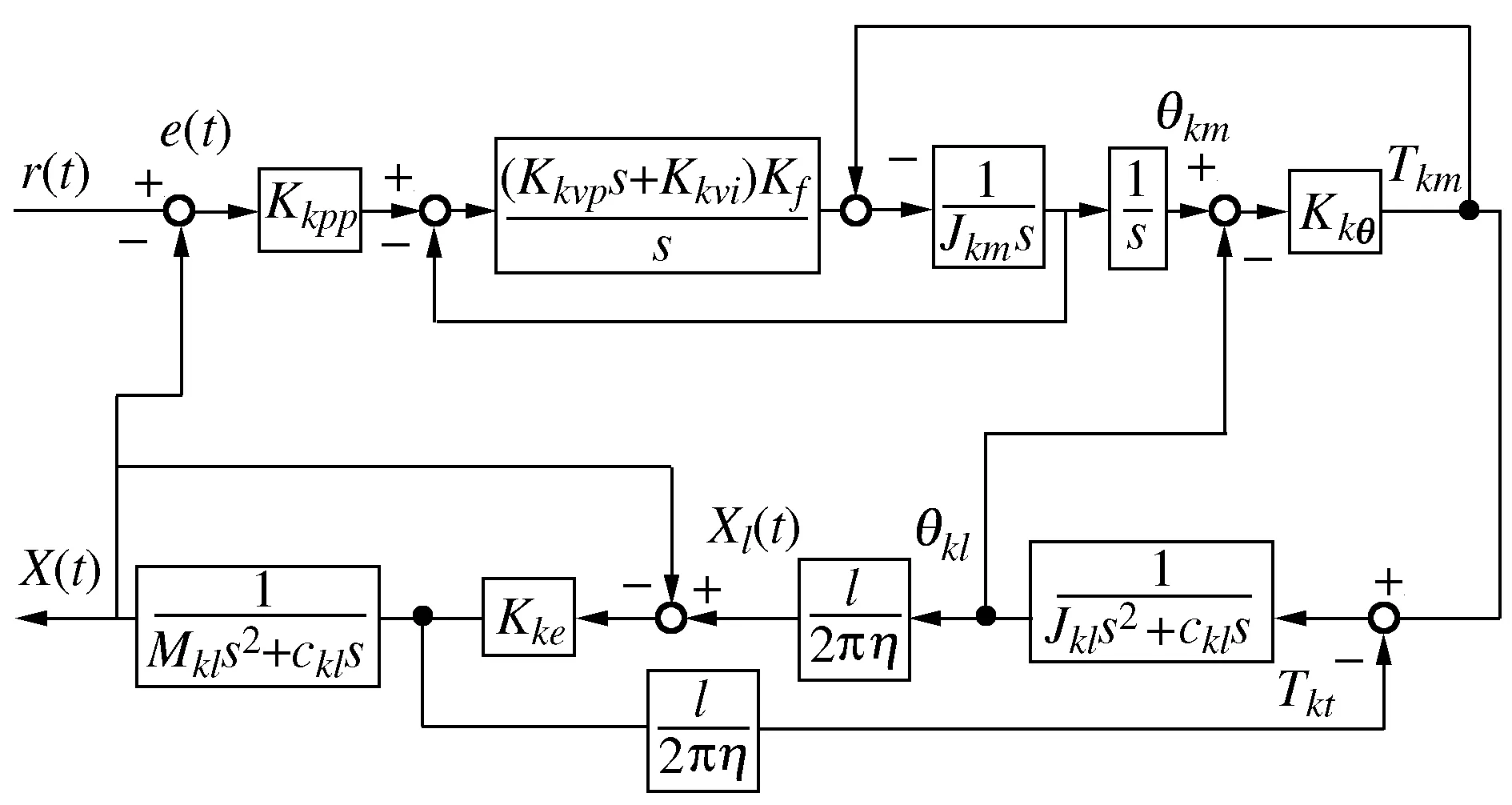
图3 进给系统传递函数方框图

如图3所示,该伺服系统共有3个控制回路,即:位置环、速度环和电流控制环。其中位置环采用比例控制,位置增益Kpp;速度环采用比例-积分控制,比例增益为Kvp,积分增益Kvi,时间常数Ti;Kf为电机的扭转系数。

根据梅森公式,输入与输出之间的传递函数为

(2)

其中:

a1=KeKfKθKvi；

a0=KeKfKppKθKvp；

b0=KeKfKθKvi；

b1=KeKfKθKvi+KeKfKppKθKvp；

b2=ClKeKθ+ClKeKfKvi+CtKfKθKvi+KeKfKθKvp+

CtKeKθR2+CtKeKfKviR2；

b3=ClCtKθ+JlKeKθ+JmKeKθ+ClCtKfKvi+

ClKeKfKvp+CtKfKθKvp+JlKeKfKvi+

KfKθKviMt+KeKθMtR2+CtKeKfKvpR2+

KeKfKviMtR2；

b4=ClJmKe+CtJlKθ+CtJmKθ+ClKθMt+ClCtKfKvp+

CtJlKfKvi+ClKfKviMt+JlKeKfKvp+KfKθKvpMt+

CtJmKeR2+KeKfKvpMtR2；

b5=JmKeMtR2+ClCtJm+JlJmKe+JlKθMt+

JmKθMt+CtJlKfKvp+ClKfKvpMt+JlKfKviMt；

b6=CtJlJm+ClJmMt+JlKfKvpMt；

b7=JlJmMt。

由于该系统为单位反馈系统,输入与偏差之间的传递函数为

(3)

1.2 等效刚度值计算

当机床高速运动时,进给系统的刚度与阻尼值不断改变,系统中的刚度和阻尼值可以用以下关于进给信号的速度和加速度表示。

Kθ等于联轴器扭转刚度与滚珠丝杠扭转刚度串联，即

(4)

其中：

式中：lc为联轴器长度；Gc为联轴器切变模量；Dc为联轴器直径；Gs为滚珠丝杠切边模量；Ds为滚珠丝杠直径。

Ke等于滚珠丝杠轴向刚度Ks,丝杠螺母副结合面处等效刚度Knut和丝杠轴承结合面处的等效刚度串联Klb、Krb。

(5)

式中:E为弹性模型；L为滚珠丝杠安装间距；Kh为类刚度系数；α为接触角；φ为丝杠螺旋角；D0为滚珠直径；i为单个螺母中滚珠圈数；P为滚珠丝杠预紧力；F为轴承预紧力；Z为轴承滚珠个数；β为轴承接触角；N为单边轴承个数。

1.3 等效阻尼值计算

Ct可采用在一个振动周期内能量消耗相等的方法进行求得[20]:

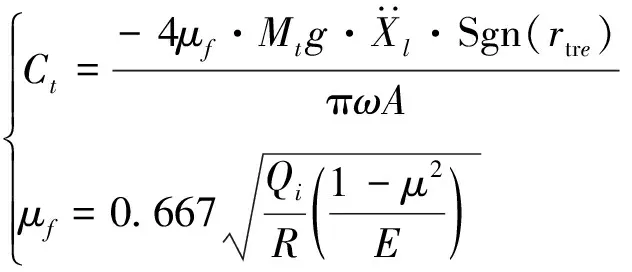
(6)

式中:μf为干摩擦因数；Sgn(rtre)为符号函数；ω为振动圆频率；A为振动幅度值；μ为泊松比；E为弹性模量；R为导轨副单个滚珠半径；Qi为单个滚珠的受力。

1.4 时变系统的建模求解方法

将式(4)～式(6)代入式(2)中,该系统是一个状态连续时变系统,可采用状态空间方程进行求解式(2),其时变微分方程为

(7)

将式(7)左边保留微分方程输出信号的高阶项则有

(8)

基于状态空间法选择中间状态变量:

(9)

那么可以得到对应的一阶微分方程组:

(10)

式(10)采用数值求解的方法比较困难,这里建立其微分方程的仿真模型如图4所示,采用MATLAB里的Simulink仿真模块进行求解。

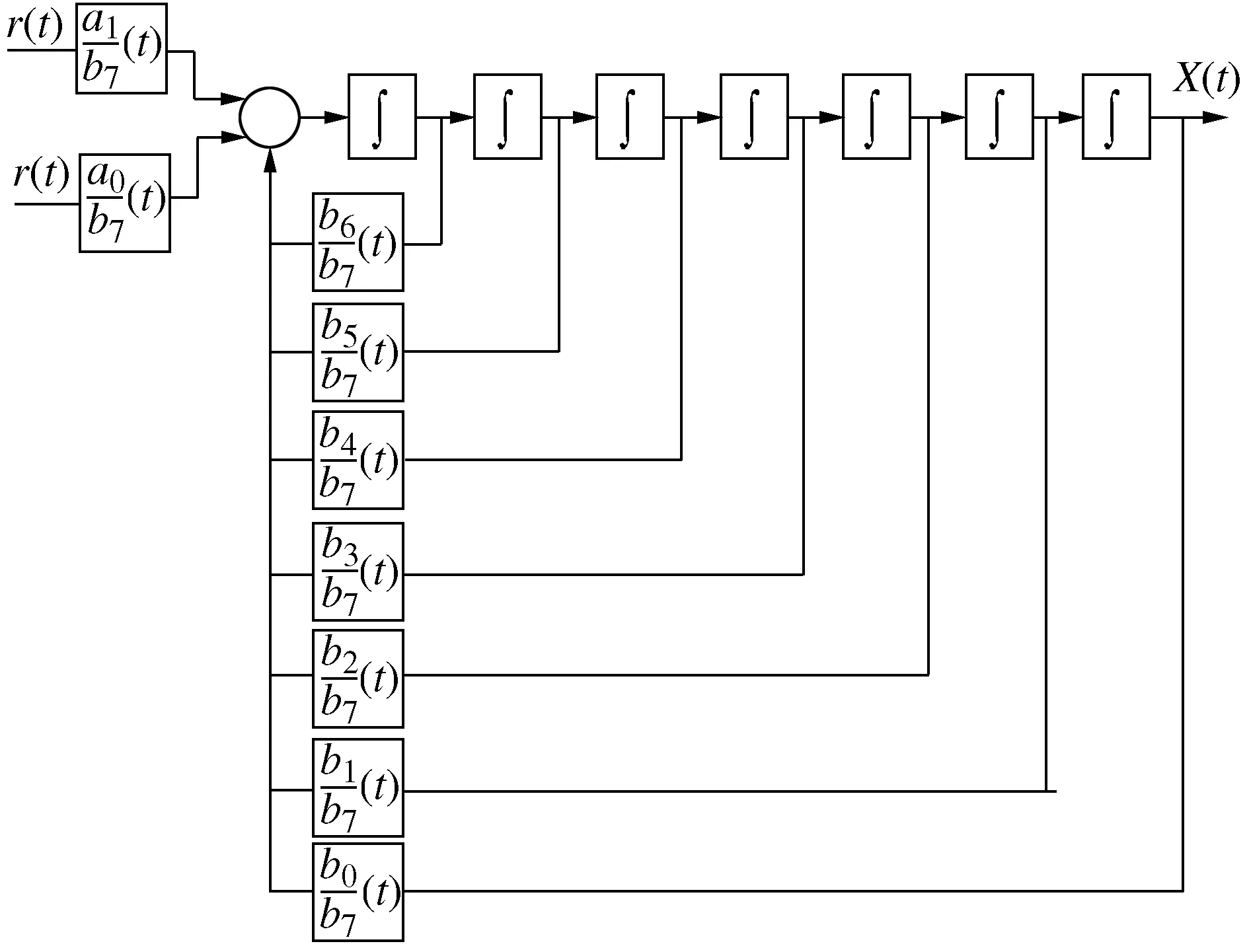
图4 时变系统的仿真模型

2 仿真分析与试验验证

2.1 仿真分析

图5 卧式加工中心结构示意图

以某机床厂生产的THC6350IV双转台卧式加工中心X轴传动系统为研究对象,分析在不同的进给速度、加速度情况下,机床伺服系统的动态误差变化规律。机床结构示意图如图5所示。

X轴进给机构具体参数如表1所示。

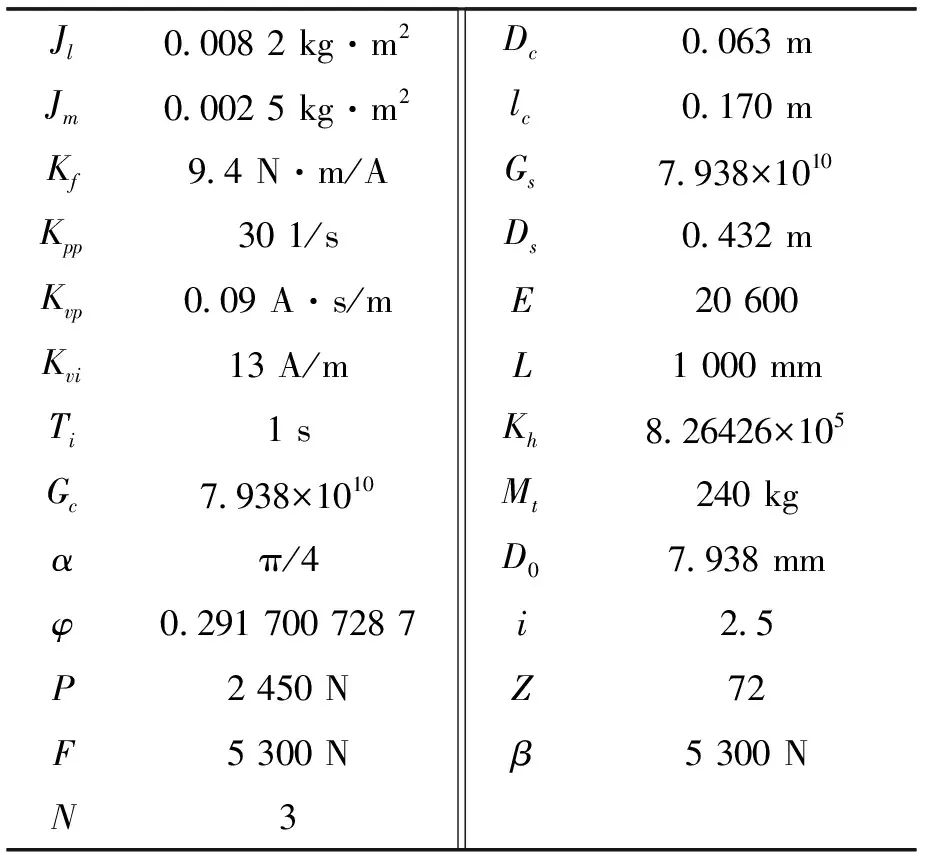
表1 系统参数

当正弦信号为r(t)=100sin(2πt),t∈[0,1],将表1中机床的数据代入相关公式进行计算,得到等效刚度值在上述指令下随时间的变化规律,如图6所示。

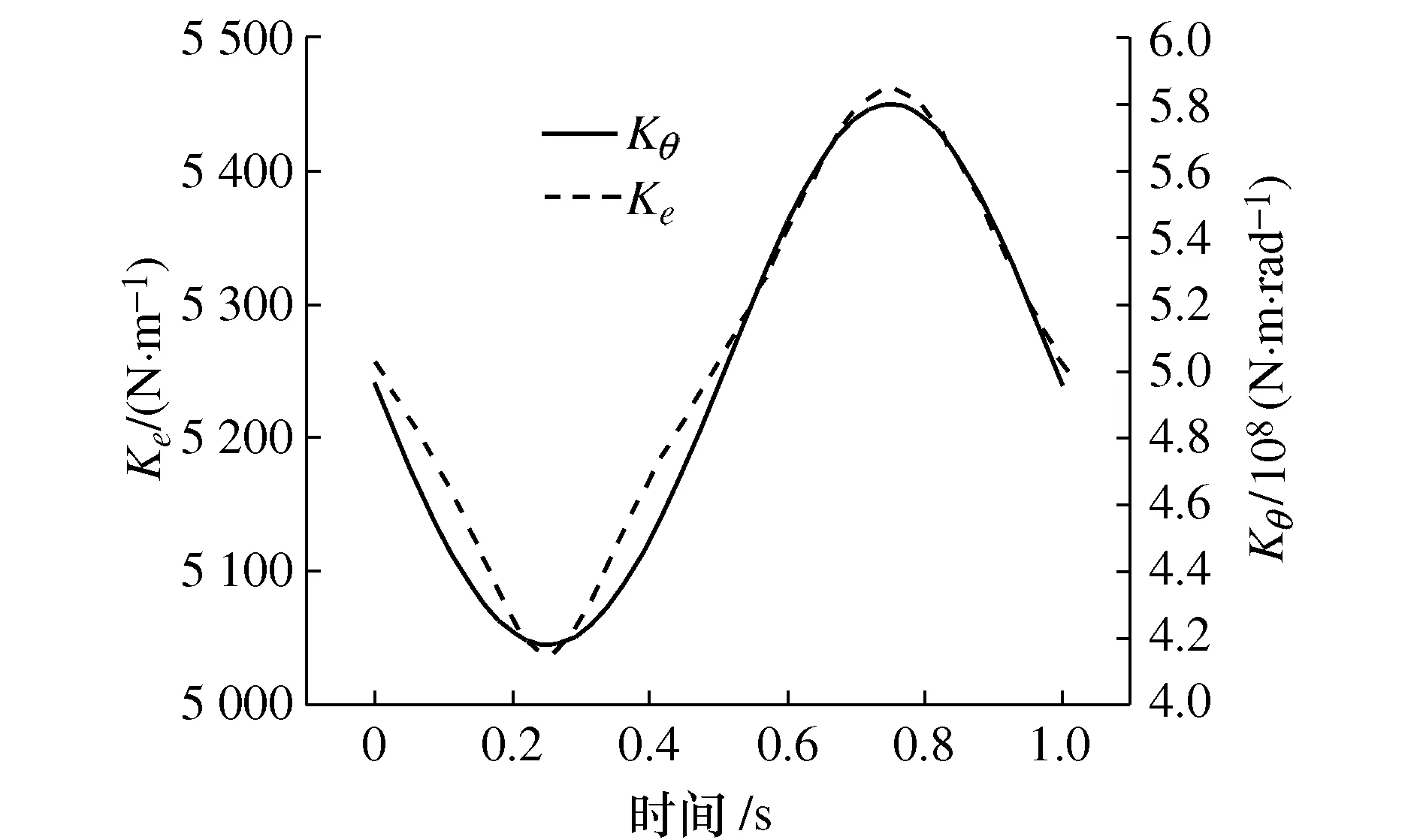
图6 等效刚度值随时间变化规律

等效阻尼值在上述指令下随时间的变化规律,如图7所示。

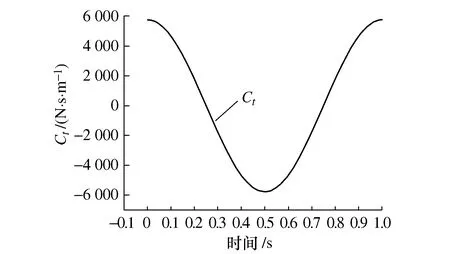
图7 等效阻尼值随时间变化规律

进给系统在上述指令下3个不同时间瞬时由于系统参数变化所导致的的频率响应变化,如图8所示。

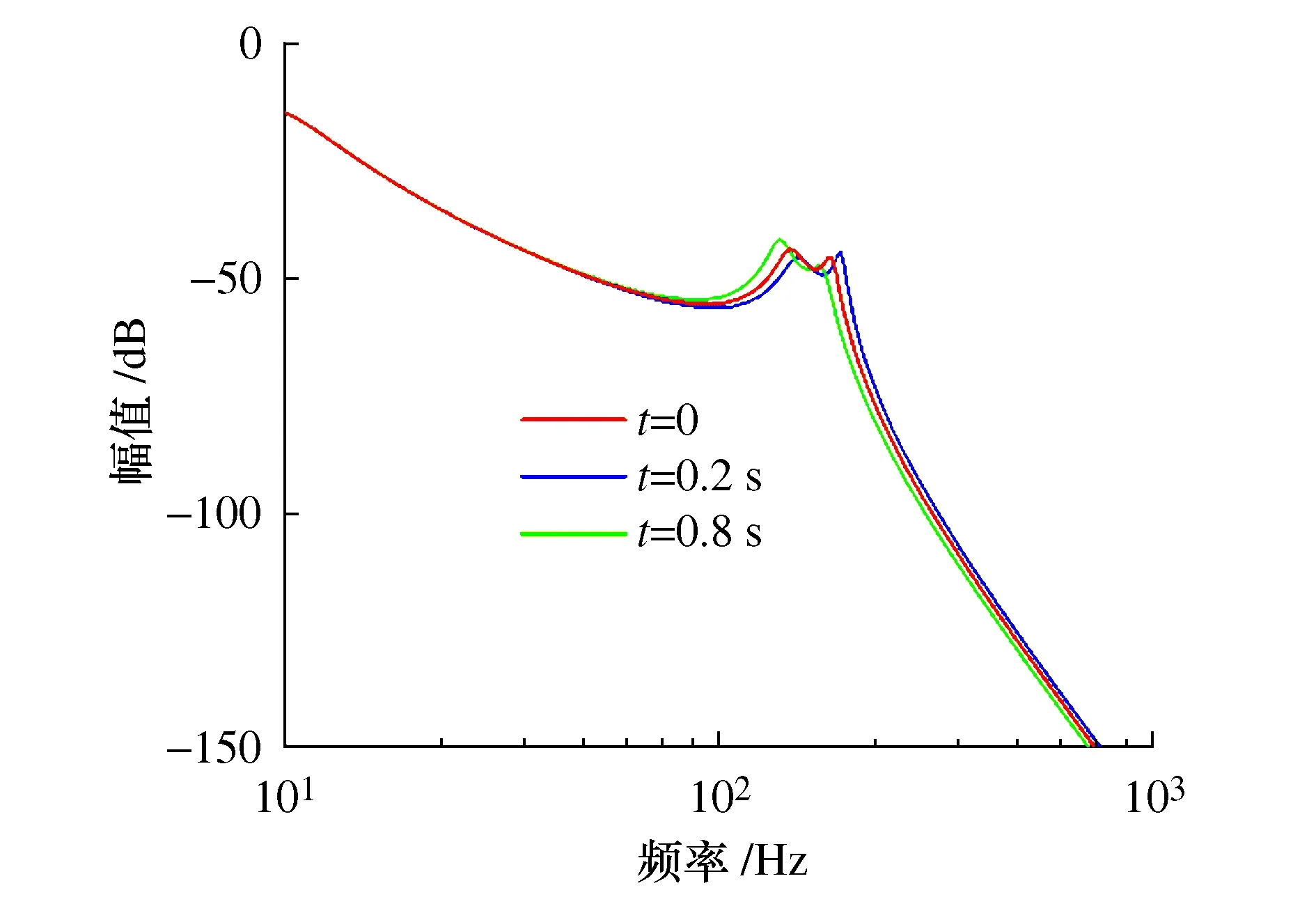
图8 系统频率响应变化

由图8可以看出,在不同时刻下机床加减速造成进给机构系统刚度、阻尼改变,系统的动态性能也随之发生改变。若仅采用动力学参数辨识法获得的刚度、阻尼值将不能反映机床机械系统的时变特性,静态情况下建立的机床伺服系统误差模型也不够准确。

运用MATLAB软件仿真图4的时变特性模型,得到本文建立的模型伺服系统的时变动态误差输出值和当系统参数取固定值传统伺服模型的误差输出值对比图,如图9所示。

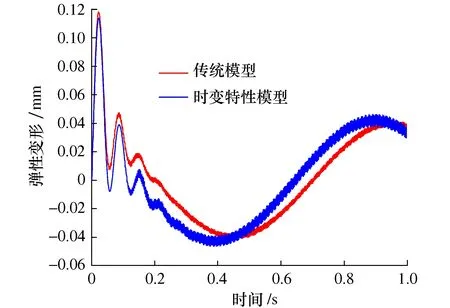
图9 伺服系统传统模型输出值与时变模型输出值对比图

由图9可知,在大多数时刻基于时变特性的进给轴伺服动态误差比传统的伺服进给系统动态误差要大,因此考虑时变特性的进给轴伺服动态模型更能准确的反应机床高速运动中的伺服动态误差变化规律。

2.2 试验验证

为验证上述预测模型的准确性,采用球杆仪对五轴卧式加工中心XYB三轴联动进行圆轨迹检测,研究不同进给速度下变化对机床综合误差的影响规律。XYB三轴联动圆度误差检测原理如图10所示。根据球杆仪自身的特点,球杆仪高速检测得到的误差主要由机床各部件的几何误差和伺服系统的伺服动态误差两部分组成。

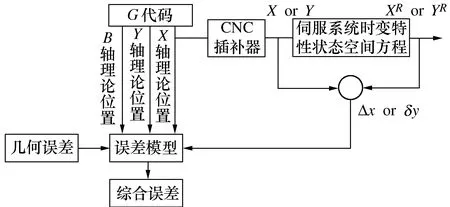
图10 XYB三轴联动综合误差检测原理

试验装置如图11所示,球杆仪安装在回转工作台上,A轴置于90°,XYB三轴联动走圆轨迹进行综合误差的检测。XY轴在不同的进给速度下(100 mm/min、1 000 mm/min、3 000 mm/min、5 000 mm/min)配合B轴联动运动画圆,球杆仪杆长设置为100 mm。研究表明,机床低速运转下机床误差主要表现为几何误差,因此在进给率100 mm/min下采集每个轴的位置与编码信息,计算机床的几何误差。

图11 试验装置

2.3 试验结果

图12～图14是XY轴进给速度分别为1 000 mm/min、3 000 mm/min和5 000 mm/min时,球杆仪检测得到的圆轨迹结果图。

图12 速度为1 000 mm/min时圆轨迹图

图13 速度为3 000 mm/min时圆轨迹图

图14 速度为5 000 mm/min时圆轨迹图

2.4 结果分析

由图9可以看出,虽然基于时变特性的进给轴伺服动态误差模型的动态误差与传统的伺服进给系统动态误差变化趋势一致,进给速度增加,伺服动态误差变大,但是由于进给系统的刚度,阻尼值每个时刻不断改变,基于时变特性的进给轴伺服动态误差在每个时刻均比传统的伺服进给系统动态误差要大,仅仅考虑静态情况下获取系统参数的伺服动态误差模型将不再适用于高变速情况下机床伺服动态误差建模,而本文提出的基于时变特性的进给轴伺服动态误差模型将更适用于高变速情况下的伺服动态误差建模。

由图12可以看出,当进给速度为1 000 mm/min时,球杆仪波动轨迹幅度不是很大,误差主要表现为机床的几何误差与伺服滞后误差,与本文模型预测趋势规律相一致。

由图13和图14可以看出,当机床的进给速度增大,球杆仪测量轨迹波动变大。在机床几何误差高度低速变化不大的情况下,说明机床伺服动态误差不断加大,主要表现为机床两轴联动伺服系统不匹配、滞后和反向跃冲,再一次说明了文本预测模型可以很好的预测机床联动的综合误差变化规律。

综上所述,本文提出对五轴卧式加工中心几何误差和时变特性的伺服动态误差综合建模与检测方法能够很好的预测机床误差在不同进给速度下的变化趋势,为机床的实时补偿策略提供一种思路,具有一定的适用性。

3 结论

本文建立了考虑机床进给机构时变特性的传动系统动力学集中参数模型,仿真分析了速度,加速度改变情况下的机床进给机构伺服动态误差的变化规律,并进行了相应的实验验证。仿真分析和实验分析都表明机床进给机构再高速运动过程中存在时变特性,因此准确地建立机床的时变特性进给轴伺服系统模型具有很强的意义。

首先,基于时变特性的进给轴伺服动态误差在某些时刻比传统的伺服进给系统动态误差要大,提出的基于时变特性的进给轴伺服动态误差模型将更适用于高变速情况下的伺服动态误差建模。

其次,本文建立的机床时变特性模型能够很好的预测机床在不同进给速度下的变化规律,可以为机床的实时补偿策略奠定一定的基础。

最后,机床的进给速度越大,球杆仪测量轨迹波动变化越大,说明机床伺服动态误差不断加大,也说明机床高速运动下的误差表现形式主要为伺服动态误差,因此需要准确的建立机床伺服动态误差模型。