应用Volterra级数识别液阻悬置非线性阻尼参数

2022-03-15甄冬高中正刘晓昂

机械科学与技术 2022年1期

甄冬,高中正,2,刘晓昂*，,2

(1. 河北工业大学机械工程学院,天津 300130;2. 天津市新能源汽车动力传动与安全技术重点实验室,天津 300130)

动力总成是引起汽车振动的主要振源,需要悬置结构这一非线性减振隔振元件对其进行处理。目前在汽车上应用最广泛的悬置结构是液阻悬置,其主要是利用阻性液体往复流经液体阻尼结构产生的黏滞阻力来进行工作的,可以使运行车辆在受到低频大振幅和高频小振幅两种振动时,能合理分配适宜大小的阻尼和刚度特性来实现隔振减振的效果,所以在动特性方面较为复杂,对于其隔振减振性能的分析和优化尤为重要。因液阻悬置各组成部件的动力学参数与其减振隔振性能有影响关系,所以参数获取对于液阻悬置动态特性曲线的设计与修正具有重要意义。

液阻悬置作为一个典型的非线性系统,需要建立较为准确的非线性模型来进行描述,可以为后面包括参数识别在内的一些工作建立基础。Geisberger等[1]考虑到上腔室、解耦盘和惯性通道的非线性特性,建立了适用于低频和高频特性的液阻悬置非线性模型。Li等[2]在改善液阻悬置性能时也考虑了此模型。Christopherson等[3]建立了惯性通道-解耦盘式液阻悬置的非线性集总参数模型,将解耦盘的非线性行为引入了悬置系统。Turnip等[4]对一种四腔室的液阻悬置引入了一个气动执行机构施加的力,开发了该悬置的非线性模型。Zhou等[5]考虑了解耦膜的变刚度特性,给出了带有悬浮式解耦器的液阻悬置的一种集总参数模型。Sakong等[6]提出了“液压”模型代替常用的集总或机械模型来表示液阻悬置。

Volterra级数理论是研究非线性系统的分析方法之一,可用于解决非线性系统的建模、求解和分析等问题。刚度和阻尼参数的识别是Volterra级数理论应用的两个重要领域,基于此理论下的非线性系统刚度和阻尼参数的识别方法也应运而生[7]。Lee[8]提出了一种基于广义频率响应函数(GFRF)估计理想非线性系统参数的直接方法。Chatterjee[9]利用递推迭代法进一步发展了该方法。Peng等[10]基于非线性输出频率响应函数的概念,提出了一种多自由度非线性系统刚度和阻尼参数估计的新算法。

本文基于Volterra级数理论,以惯性通道-浮动解耦盘式液阻悬置为研究对象,提出了该液阻悬置非线性阻尼滞后角和其液体阻尼机构的非线性阻尼参数识别方法。该方法本质上属于一种间接试验法。与其包括的特征点[11]和不动点[12]法不同,特征点法和不动点法只应用了动特性曲线上的某几个点,易受选点误差的影响。而该方法在一定范围内充分利用了动特性实验的数据,可以在知道输出和部分结构参数的情况下来较为简单的获得液体阻尼机构的阻尼参数,且在一定范围的激励频率下得到的该阻尼参数识别值与实验得到的参数值之间的误差能保持在3%以内。另外由Volterra级数理论识别得到的液阻悬置阻尼滞后角已由平均法对比验证,和液体阻尼机构的阻尼参数识别结果一样表现出了较好的一致性。

1 液阻悬置的数学模型

惯性通道-浮动解耦盘式液阻悬置的特点在于它内部的液体阻尼结构是解耦盘和惯性通道。其中解耦盘存在于上下开口的金属通道内,可根据激励的幅度使流体通过或阻塞。惯性通道是一个环绕在解耦器周围的螺旋液体通道,流体可通过这里在上下腔室之间来回震荡,从而产生阻尼[13]。该液阻悬置的整体结构如图1所示

基于Christopherson的研究[3],建立如图2所示的浮动解耦盘式液阻悬置的集总参数模型。

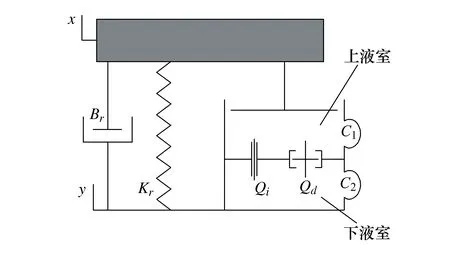
图2 液阻悬置集总参数模型

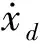
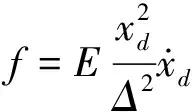
(1)

式中：E是解耦盘的非线性阻尼参数；Δ为解耦盘的一半自由行程。

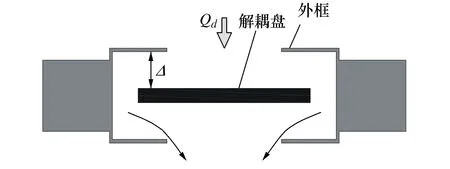
图3 浮动解耦盘的结构图

基于液阻悬置的动量、流量和连续性方程,再考虑上解耦通道闭合的影响,可以得到惯性通道-浮动解耦盘式液阻悬置的非线性数学模型为:

(2)

式中：C=AP/C1；角标i和d分别代指惯性通道和解耦盘；M为流体质量；x为液柱位移输出；B为液体阻尼机构的线性阻尼参数；AP为主簧的等效面积；C1和C2分别为上、下腔室的体积柔度；K为上、下腔室体积刚度之和。

2 Volterra级数理论

以f(t)为输入激励,x(t)为输出响应的一般物理系统的输入输出关系可由Volterra级数[9]表示为

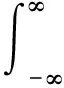
…=x1(t)+…+xn(t)+…

(3)

式中hn(τ1,…,τn)为n阶Volterra核函数,是表征各种非线性阶次的高阶脉冲响应函数。高阶频率响应函数FRF被定义为高阶脉冲响应函数的多维傅里叶变换,其形式为

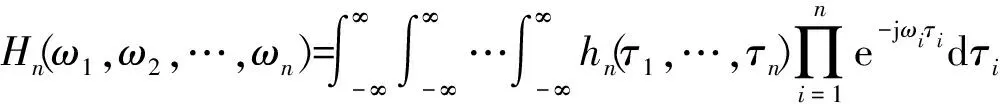
(4)

假设非线性系统受到一个输入激励

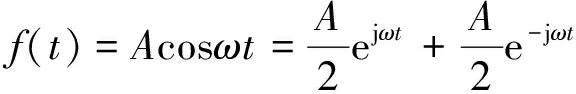
(5)

则该系统的输出响应可以表示为

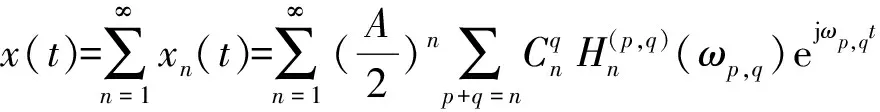
(6)

其中

(7)

对于一个非线性系统的参数化模型,系统的频率响应函数FRF可以使用谐波探测法[14]求得。因FRF只与系统结构有关而不与系统输入相关,此时可假设液阻悬置系统受到一个指数组合的输入激励来较为简单的获得FRF的结构式。

3 液阻悬置的非线性阻尼参数识别

本部分基于上文提到的Volterra级数理论识别了液体阻尼机构(解耦盘)的非线性阻尼参数以及液阻悬置系统的非线性阻尼滞后角,并又利用平均法求解了液阻悬置系统的非线性阻尼滞后角以用于后文的对比验证。

3.1 Volterra级数理论识别液体阻尼机构非线性阻尼参数

在等式(5)表示的输入激励下,该液阻悬置系统的FRF可表示为:

(8)

(9)

其中：

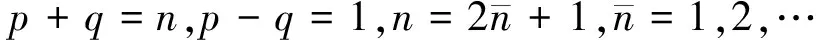
(10)

在输入信号式(5)的激励下,输出响应式(6)在频域下可由Volterra级数表示为

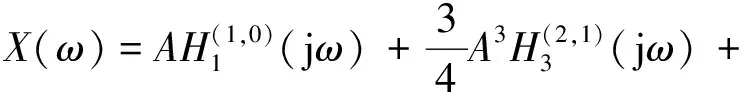
(11)

考虑到液阻悬置系统的各阶FRF在分母上是相同的,取1阶和3阶FRF,由复数的构成性质可得液体阻尼机构的非线性阻尼参数E为

现在只需再知道其结构式中的1阶和3阶FRF以及部分结构参数(一般由试验法测得)的数值,即可代入求得非线性阻尼参数这个难以直接测量的参数值。

由等式(11)可知,X(ω)是关于FRF的函数。因此使用具有不同激励幅值A的输入信号(式(5))来得到多种X(ω)的值,并忽略高阶项,就可以通过列矩阵来估算出前几阶的FRF值。在这里采用4种不同激励幅值A1、A2、A3、A4的输入信号,分别对应一次谐波响应振幅X1(ω)、X2(ω)、X3(ω)和X4(ω)。考虑到保留项数越多,FRF的估算就越精确,在这里取用等式(11)的前四项,可以列矩阵为

通过求解矩阵(13),就可以将各阶次FRF的值与其各自的结构式达成对应关系,进而由识别式(12)得到液体机构非线性阻尼参数的识别值。

3.2 Volterra级数理论识别液阻悬置非线性阻尼滞后角

假设液阻悬置系统受到正弦信号激励为

x=Asinωt

(14)

为了对非线性下的液阻悬置模型式(2)进行频率响应分析,传递力方程可被表示为

fT=KrAsinωt+BrAωcosωt+ApP1sin(ωt+φ1)(15)

式中：Kr和Br分别为主簧的动刚度和阻尼参数。所寻求的解可以用fT=FTsin(ωt+φ)表示,在使用适当的恒等式之后,等式(15)可以表示为:

(16)

式中φ为系统的非线性阻尼滞后角。

式(15)中的压力项为

(17)

基于本文提到的Volterra级数理论,在正弦信号(式(14))的激励下,可将解耦盘和惯性通道的液柱位移输出用级数表示为

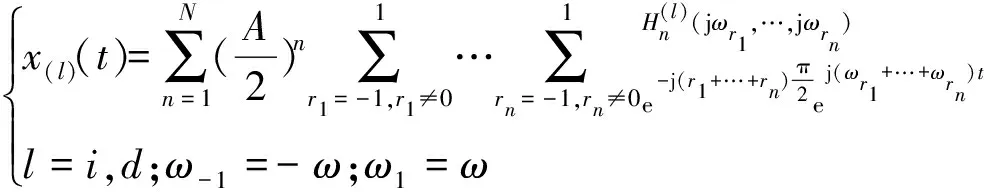
(18)

为了便于后续计算,在这里取N=3,使输出响应(式(18))近似于3阶非线性模型,并将其代入式(17)中,即可得到:

(19)

其中

忽略掉极小量的级数项,此时通过联立式(16)与式(19)即可得到该液阻悬置的非线性阻尼滞后角φ。

3.3 平均法求解液阻悬置非线性阻尼滞后角

考虑到本液阻悬置数学模型(2)中的非线性项f为高阶小量,因而对此类非线性系统常采用平均法[15]来表达出系统的输出响应,并与新提到的应用于液阻悬置的Volterra级数法进行对比验证。

当液阻悬置系统受到正弦激励式(21)时,可以认为集总参数模型(式(2))的解具有如下形式：

(21)

其中振幅和相位均为时间t的慢变函数。记φd=wτ+φd和φi=wτ+φi,因非线性项f为高阶小量,其振幅和相位在φd和φi的一个周期2π内缓慢变化,这就使式(21)在本质上是稳态的,不会随时间变化,所以需要消除方程中的时间导数,即可得到描述解耦盘和惯性通道振幅的隐式频率响应函数及相位角方程为

(22)

(23)

将等式(22)中的隐式解和式(23)的相位角代入等式(21)中,由适当的三角恒等式变换后可得到:

(24)

其中

(25)

同理联立等式(16)、式(24)即可在平均法下得到液阻悬置的非线性阻尼滞后角φ。

4 结果分析

4.1 验证液体阻尼机构的非线性阻尼参数的识别精度

由已知文献[16]确认了表1所示的该种类型液阻悬置的一组参数值,可用于本文的数值分析。

表1 由试验法获得的部分液阻悬置参数值

本文采用一数值计算软件进行仿真来验证基于Volterra级数法得到的识别公式的准确性。考虑到液阻悬置主要受到低频大振幅和高频小振幅的工作激励,因此仿真验证也会采用这两种常见的工况来进行。

在低频高幅值信号激励下,首先假设表1所示的参数已知,构建液阻悬置的数学模型,给予正弦输入激励,幅值A分别为0.2,0.3,0.4,0.5 mm,取采样时间为0.001 s,仿真时间为2 s,设定1～10 Hz的低激励频率,每隔1 Hz进行采样,可得到不同情况下的解耦盘和惯性通道的液柱位移输出(该输出在实验条件下可由流量传感器获得)。将时域输出转为频域输出,得到前3阶FRF的值,即可接着用于非线性阻尼参数E的结构式中得到其识别值。

对于解耦盘和惯性通道,其液柱位移输出响应可由示波器给出。选用其中一种激励情况(f=6 Hz,A2=0.3 mm),其时域和频域下的输出响应图如图4所示。

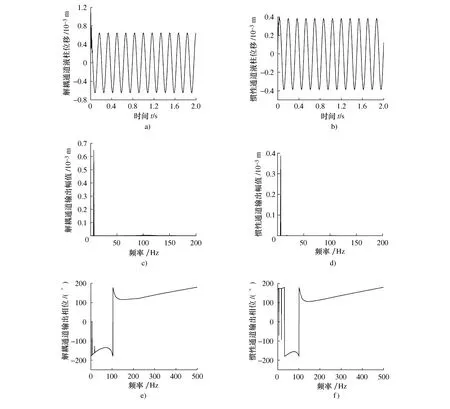
图4 解耦和惯性通道的液柱位移输出响应

在采集了各情况下的输出数据点后,可以运算得到如表2所示的统计结果。

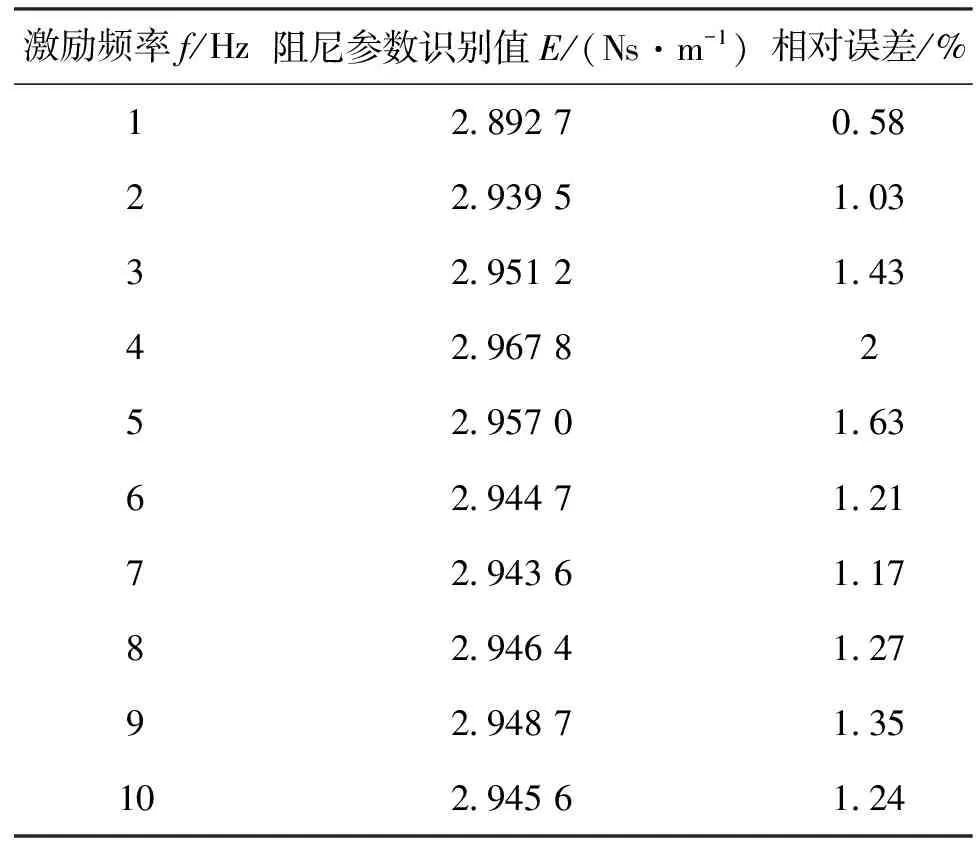
表2 低频范围内的识别值

由上述统计结果所知,在1～10 Hz的激励频率范围内得到的解耦盘的非线性阻尼参数E较标准值来说极为接近,其相对误差在3%以内。说明本文推导的非线性阻尼参数识别公式在低频高幅值激励下具有一定的准确性。

在高频低幅值信号激励下,考虑到利用Volterra级数进行识别时会在共振频率范围附近出现得值不收敛的情况[8],所以远离液阻悬置共振频率(100 Hz左右)取用20～70 Hz范围内的激励频率,设定A分别为0.02 mm,0.03 mm,0.04 mm,0.05 mm的低幅值,采样时间为0.000 5 s,仿真时间为1 s,每隔10 Hz进行采样,统计结果如3所示。可以观察到解耦盘的非线性阻尼参数E与标准值之间的相对误差依然能保持在3%左右。

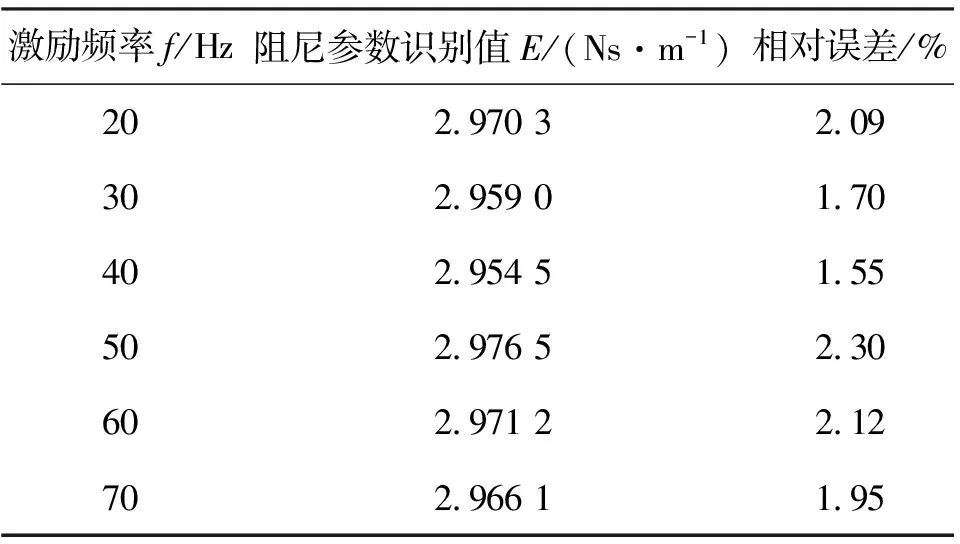
表3 高频范围内的识别值

4.2 验证液阻悬置的非线性阻尼滞后角的识别精度

对于液阻悬置的非线性阻尼滞后角,可参照分别由Volterra级数法和平均法得到的推导公式来获得,并进行比较验证。为了便于比对分析,用表1提供的阻尼参数试验数据用于接下来的数值分析。取激励振幅A=0.2 mm,激励频率范围为0～200 Hz且每隔10 Hz取样,其他已知参数不变,可绘制出在两种方法求解下的液阻悬置非线性阻尼滞后角随激励频率变化的曲线图。

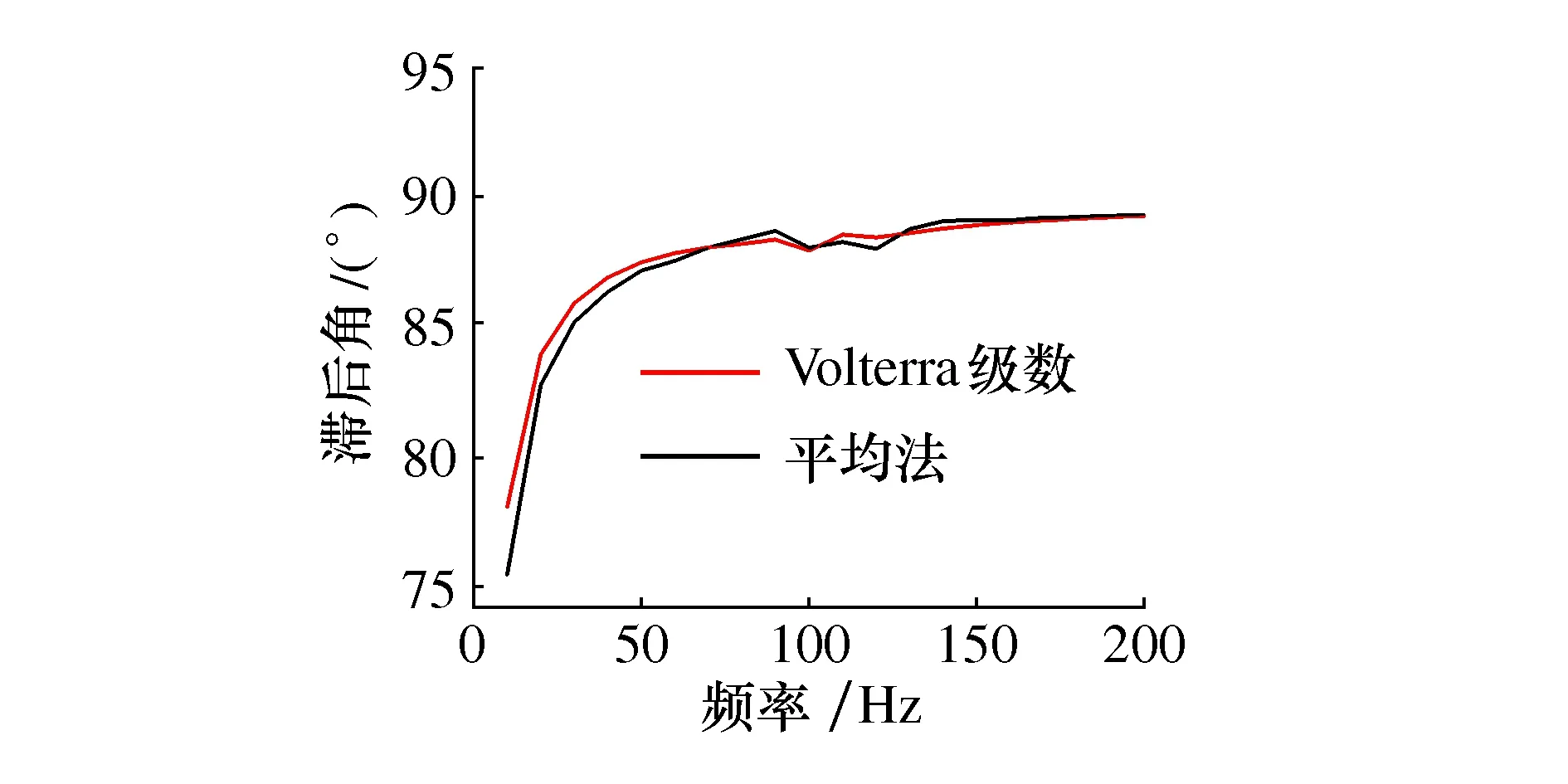
图5 液阻悬置阻尼滞后角曲线图

由图5可知,随着激励频率的变化,由两种方法得到的液阻悬置非线性阻尼滞后角的变化曲线是基本吻合的,可以证明Volterra级数法具有替换平均法进行求解的意义。因平均法一般受限于非线性项的性质,所以难以较大范围的进行应用,而此时的Volterra级数法就不会受到这个限制,可以直接以级数的方式表示出系统的输出响应来用于后续液阻悬置阻尼滞后角的计算。另外可以知道,当选用较多阶数的Volterra级数模型时,对于液阻悬置阻尼滞后角的识别会更精确。