结合POE旋量理论的三轴立式加工中心几何误差建模方法
2022-03-15余文利邓小雷谢长雄王建臣
余文利,邓小雷,谢长雄,王建臣
(1. 衢州职业技术学院 机电工程学院,浙江衢州 324000;2. 浙江大学 浙江省三维打印工艺与装备重点试验室,杭州 310027;3. 衢州学院 机械工程学院,浙江衢州 324000)
影响机床加工精度的因素包括几何误差、热误差、切削力误差、伺服控制误差等,其中几何误差和热误差约占总误差的65%[1]。几何误差对加工质量有重大影响,是导致机床误差的主要因素。而几何误差具有系统性、可重复性和可测量性等特点,使得误差补偿成为一种经济有效的提高机床加工精度的重要手段[2]。
几何误差补偿技术的前提之一是几何误差建模,通过建模可以为补偿提供模型支持。当前几何误差建模最常用的方法是基于机床运动链的分析,通常以机床床身为基础,将运动链分为两个子链,一个子链用于驱动刀具,另一个子链用于移动工作台。对其进行运动学建模的最常用的方法为多体系统理论结合齐次坐标变换法(Homogeneous transformation matrix, HTM)[3]。金增楠等[4]基于多体系统理论建立拓扑结构及低序体间阵列,并据此获得镗削系统空间误差模型。赵强强等[5]运用多体系统理论,构建任意结构机床拓扑结构与低序体阵列,并提出了机床运动轴连接支承件相对运动矩阵与机床支承件连接矩阵概念,建立了获取运动轴误差传递链的数学模型。杨泽青等[6]在热稳态条件下基于多体系统理论和HTM方法建立包含几何误差和伺服动态误差的综合误差模型。Wu等[7]基于HTM和多体系统理论,建立了仅考虑多轴数控机床平动轴的位置误差模型。文献[8]通过HTM构造相对于坐标系的相对运动矩阵,基于齐次变换推导出三轴机床的几何误差模型。董泽园等[9]采用HTM方法基于18项和21项几何误差元素构建三轴数控机床的几何误差模型,并对这两种误差补偿的有效性进行了系统性的分析比较。Xiang等[10]基于多体系统理论和HTM方法提出了一种用于多机床的空间误差广义模型和分布式误差补偿技术。赵壮等[11]采用阿贝原则和布莱恩原则对HTM几何误差补偿模型进行优化,进一步改善了空间误差的补偿精度。多体系统理论结合HTM方法虽然在机床几何误差建模中得到大量成功应用,但是仍然存在以下局限性:1) HTM建模方法将机床各部件看作刚体,各部件需要建立单独的坐标系,一个运动轴的综合齐次变换矩阵包括位置矩阵、位置误差矩阵、运动矩阵、运动误差矩阵[12],进行矩阵变换时存在潜在的奇异性问题;2) HTM误差模型与机床拓扑结构密切相关,机床结构的微小变化就会使得HTM误差模型失效。近年来,POE旋量理论[13]已在机器人技术领域得到广泛使用,国内外学者相继将该理论应用于构建机床的运动学模型,并在此基础上推导出几何误差模型。Zhao等[14]将几何误差源用旋量表示,综合模型的计算结果为误差旋量的总和,并建立了基于旋量理论的几何误差模型。Tian等[15]采用旋量理论构建几何误差模型时考虑了垂直度误差的影响,并用六维向量来表示误差元素。Zhao和Tian的研究中没有对每个轴的基本误差元素进行详细描述,同时,在构建误差模型时直接使用旋量,而没有使用旋量的指数矩阵,并且没有详细解释这些旋量的集成方式,使得建模过程不够清晰和系统[14-15]。
本文以三轴立式加工中心为研究对象,基于POE旋量理论建立一个系统的几何误差模型,以综合三轴立式加工中心的所有几何误差。首先,建立各个轴的基本误差元素的旋量和POE模型,从几何意义的角度,将各个轴的6个基本误差元素分为3组,每组用一个误差旋量表示,综合3个误差旋量建立各个轴误差POE模型,所建立的POE模型确保了变换矩阵是齐次的,并且符合误差元素的几何定义;其次,在POE模型中考虑垂直度误差,通过分析垂直度误差的几何属性,提出两种获得垂直度误差POE模型的方法;此外,将立式加工中心的拓扑结构作为旋量和POE模型相乘次序的确定原则。最后,在北京精雕Carver800T三轴立式加工中心进行几何误差辨识和建模实验来验证本文模型的可行性和有效性。
1 基于POE旋量理论的三轴立式加工中心几何误差建模
1.1 旋量理论和POE建模
Chasles定理[16]证明了一个刚体从一个位姿到另一个位姿运动分为两部分:围绕空间某一直线的旋转运动及沿平行于该直线的平移运动,这种复合运动称为螺旋运动。而运动旋量即为螺旋运动的无穷小量,在Plücker坐标系中,单位旋量表示为
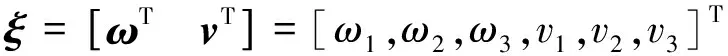
(1)
式中:ω为瞬时角速度;v为线速度。
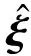
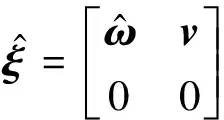
(2)

刚体的复合运动包含旋转和平移[17],假设刚体坐标系和参考坐标系之间的向量为q,则刚体的齐次变换矩阵为
(3)
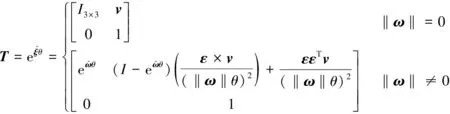
(4)

(5)
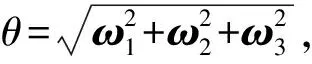
(6)
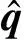
(7)
此外,可以采用POE旋量理论建模来表示开放链机器人的正向运动学,对于n自由度机器人,正向运动学指数积[20]为

(8)
式中T(0)表示初始变换矩阵。
从上述推导步骤可知,与传统的基于HTM方法的运动学建模不同,基于POE旋量理论的运动学建模方法优势如下:1) 避免了HTM建模方法中对各部件建立局部坐标系,整个过程只需建立一个全局参考坐标系,解决了矩阵变换时存在的奇异性问题;2) 运动旋量指数可以方便地描述刚体的运动,其清晰的物理意义可以更好地表达刚体运动的空间几何特性,从而简化了串联机构的运动学分析。
鉴于此,本文将POE旋量理论应用于三轴立式加工中心的运动学建模,并在此基础上建立综合几何误差POE模型。
1.2 几何误差元素分析
全局坐标系中机床的每个部件(如平动轴、主轴、铣头等)都有运动旋量和误差旋量,由这些组件的旋量可以组成机床的运动链,同时也是机床拓扑结构的基础。通过工作台坐标系获得的工件几何误差被选作参考坐标系。通过对拓扑结构的分析,将误差旋量和运动旋量的指数矩阵相乘,得到几何误差模型。
三轴立式加工中心包含21项几何误差元素[21],分别为定位误差、直线度误差、角度误差和垂直度误差,如表1所示。

表1 三轴立式加工中心的几何误差元素
表1中,δ代表线性误差,ε代表角度误差,S代表垂直度误差。误差变量均有两个下标,第一个下标表示误差的方向,第二个下标表示所在轴的名称,例如:δxy表示Y轴在X方向的线性误差,εxz表示Z轴围绕X轴的角度误差。以下将这些几何误差元素用旋量表示,然后基于POE旋量理论构建综合几何误差POE模型。
1.3 基于旋量的几何误差建模
三轴立式加工中心有3个平动轴,其单位运动旋量为
ξb=[0,0,0,sx,sy,sz]T
(9)
式中单位向量s=[sx,sy,sz]T表示平动轴的运动方向。其运动指数矩阵eξb可以表示为
(10)
以下用ξx、ξy和ξz分别表示X轴、Y轴和Z轴的运动旋量,x、y和z分别表示各个轴的运动位移。则相应的指数矩阵分别为每个轴的理想变换矩阵,各个轴的运动旋量和指数矩阵分别为:
(11)
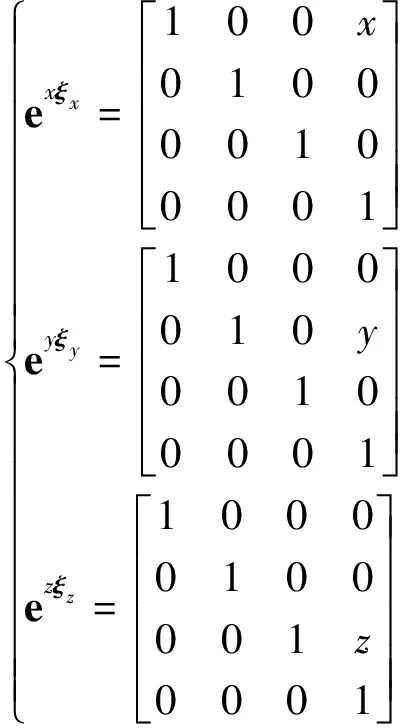
(12)
由于制造和装配缺陷,机床运动轴在平移过程中的实际运动位姿与理想运动位姿存在偏差,此偏差被称为几何误差[22]。通常,由于刚体具有六个自由度,因此六项误差元素可用于描述运动轴的几何误差[23],包括1项定位误差,2项直线度误差和3项角度误差(俯仰、偏摆和滚转)。Moon等[24]使用旋量理论将六项误差元素描述为模块化误差旋量,即使用一个旋量来表示所有的误差元素,其定义形式为meξe=[εx,εy,εz,δx,δy,δz]T,因为没有考虑误差元素的几何定义,该旋量指数矩阵无法正确表示6个基本几何误差元素。
图1所示为平动轴的6项基本几何误差元素,以X轴为例,将这6项误差元素根据方向分为3组,每组分别采用一个旋量表示。第一组包含定位误差δxx和滚动角度误差εxx,其对应的旋量为ξxx;第二组包含水平直线度误差δyx和俯仰角度误差εyx,其对应的旋量为ξyx;第三组包含竖直直线度误差δzx和偏摆角度误差εzx,其对应的旋量为ξzx。
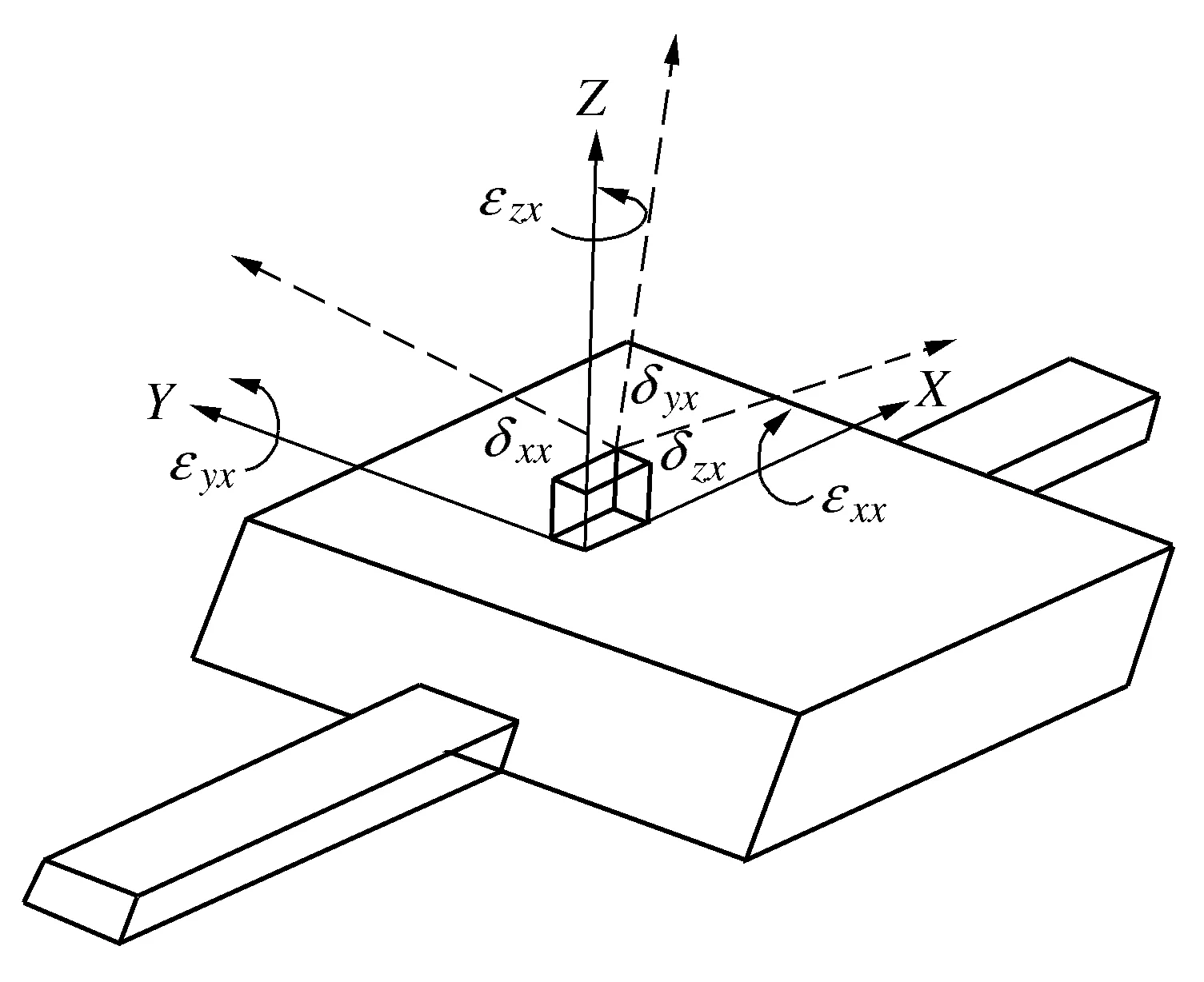
图1 平动轴的6项基本几何误差
3个旋量分别表示为:
(13)
(14)
式中:s=sin;c=cos。
X轴不包含垂直度误差的误差POE模型为

(15)
式中ξxe为X轴几何误差元素综合旋量。
同理,Y轴和Z轴的误差旋量和误差POE模型为:
(16)
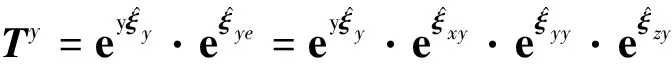
(17)
(18)
(19)
1.4 垂直度误差建模
由于实际轴与理想轴的偏差,相邻轴之间的角度不等于90°,即存在垂直度误差。垂直度误差可以解释如下:由于将Y轴定义为与参考坐标系对齐,因此对于实际的Y轴不存在垂直度误差。根据上述解释,可知三轴数控机床存在3个垂直度误差,分别是X轴与Y轴之间的Sxy,Y轴与Z轴之间的Syz以及X轴与Z轴之间的Sxz,如图2所示,由实际X轴和Y轴形成的平面称为X-Y参考平面,实际X轴只有垂直度误差Sxy;同时,对于实际的Z轴,存在另外两个垂直度误差。
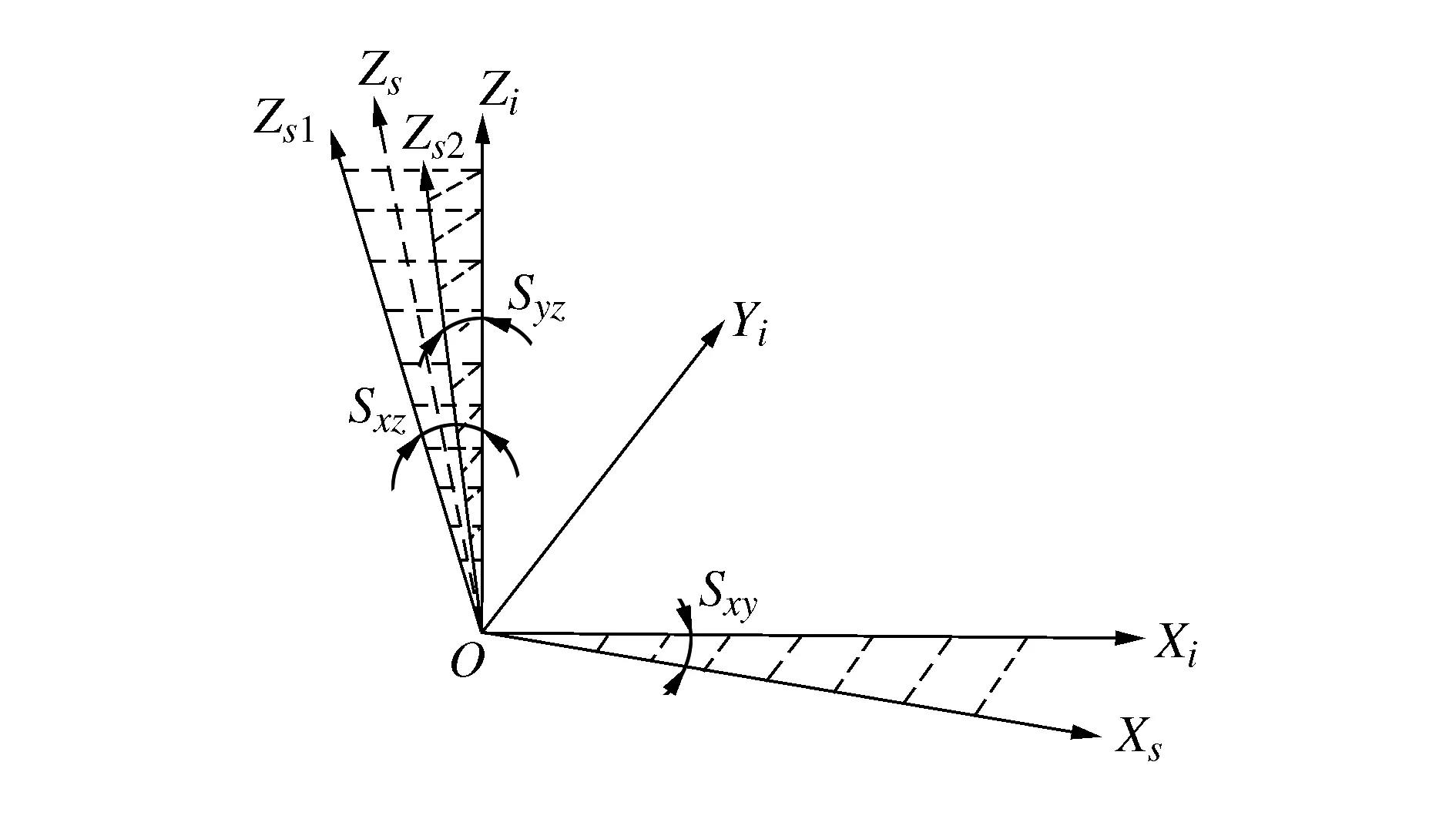
图2 三轴立式加工中心垂直度误差分布
以X轴为例,理想单位旋量ξxi为
ξxi=[0,0,0,1,0,0]T
(20)
由于存在垂直度误差Sxy,实际单位旋量ξxs为
ξxs=[0,0,0,cos(Sxy),-sin(Sxy),0]T
(21)

(22)
此外,伴随矩阵可用于表示坐标变换。根据式(7),参考坐标系围绕理想Z轴旋转一个角度,该过程可以表示为:
(23)
式中第二个下标r表示围绕由第一个下标表示的轴的旋转旋量,该轴表示理想轴。
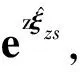
(24)
与伴随矩阵坐标变换方法一样,参考坐标系首先围绕理想Y轴旋转一个角度,然后围绕理想X轴旋转一个角度。上述变换可表示为:
(25)
式中:ξxr=[1,0,0,0,0,0]T是围绕理想X轴转动的单位旋转旋量;ξyr=[0,1,0,0,0,0]T是围绕理想Y轴转动的单位旋转旋量。
1.5 基于拓扑结构的几何误差建模
以XYFZ三轴数控机床为例,结构原理如图3a)所示,图3b)为基于多体系统理论所获得机床的拓扑结构,拓扑结构可应用于几何误差的POE建模。

图3 XYFZ型多轴数控机床结构示意图
在机床理想状况下,因为不考虑运动误差,指数矩阵相乘顺序为Xi→Yi→Zi。理想POE模型为

(26)
式中:x表示X轴的伺服控制位置,即X轴的移动距离;y和z分别表示Y轴和Z轴的位置。因参考坐标系位于工作台上,因此X轴和Y轴的坐标为负数。Ti也可以表示刀尖的理想齐次坐标。
在实际情况下,机床存在各种几何误差,影响机床的加工精度。几何误差元素的误差旋量包括垂直度误差旋量、各平动轴线性误差旋量和角度误差旋量,其误差指数矩阵相乘顺序如图3b)所示为:Xe→Xi→Ye→Yi→F→Zi→Ze,即
(27)
式中旋量ξF=[0,0,0,0,0,0]T表示机床床身。
刀尖误差是理想值与刀尖实际齐次坐标的偏差,误差变换矩阵E为
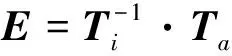
(28)
设E的3个分量分别为Ex、Ey和Ez,则
[Ex,Ey,Ez,1]T=E·[0,0,0,1]T
(29)
因为三轴立式加工中心只有平动轴而没有旋转轴,刀具姿态误差无法进行补偿,在此不予考虑。三轴三轴立式加工中心综合误差模型即为刀尖的位置误差,使用小角度近似假设,则几何误差模型为:
Ex=-δxx-δxy+δzxεyx+δzyεyx-δyyεxyεyx+δzyεyy+xSxyεzx-δyyεzx-δzyεxyεzx-(z+δzz+δyzεxz)×
(εyx+εyy-εxyεzx)+[1+εzx(εxyεyy-εzy)-εyx(εyy+εxyεzy)]-y[εzx+(1-εyxεyy)εzy+
εxy(εyx+εyyεzxεzy)]+(-zSyz+δyz-δzzεxz)[εzx+(1-εyxεyy)εzy+εxy(εyx+εyyεzxεzy)]
(30)
Ey=y-δyx-δzxεxx+εxx(-δzy+δyyεxy)+(-δxy+δzyεyy)(εxxεyx-εzx)+x(-εxxεyx+εzx)+
xSxy(1+εxxεyxεzx)-(δyy+δzyεxy)(1+εxxεyxεzx)+(z+δzz+δyzεxz){εxy+εyyεzx+εxx[1+εyx(-εyy+εxyεzx)]}+
(-zSxz+δxz+δzzεyz)(εxxεyx-εzx+(1+εxxεyxεzx)(εxyεyy-εzy)+εxx(εyy+εxyεzy))-
y[(εxxεyx-εzx)εzy+εxx(-εxy+εyyεzy)+(1+εxxεyxεzx)(1+εxyεyyεzy)]+
(-zSyz+δyz-δzzεxz)[(εxxεyx-εzx)εzy+εxx(-εxy+εyyεzy)+(1+εxxεyxεzx)(1+εxyεyyεzy)]
(31)
Ez=-z-δzx-δzy+δyxεxx+δyyεxy-x(εyx+εxxεzx)+(-δxy+δzyεyy)(εyx+εxxεzx)+
(δyy+δzyεxy)(εxx-εyxεzx)+xSxy(-εxx+εyxεzx)+(z+δzz+δyzεxz)[1+εyx(-εyy+εxyεzx)-εxx(εxy+εyyεzx)]+
(-zSxz+δxz+δzzεyz)(εyx+εyy+εxxεzx+(-εxx+εyxεzx)(εxyεyy-εzy)+εxyεzy)-
y[-εxy+εyyεzy+(εyx+εxxεzx)εzy+(-εxx+εyxεzx)(1+εxyεyyεzy)]+
(-zSyz+δyz-δzzεxz)[-εxy+εyyεzy+(εyx+εxxεzx)εzy+(-εxx+εyxεzx)(1+εxyεyyεzy)]
(32)
忽略了2阶和高阶误差项后,三轴数控机床一阶误差模型为:
(33)
2 算例与试验验证
2.1 几何误差测量与辨识
北京精雕Carver800T三轴立式加工中心为XYFZ型机床,选择美国光动公司MCV-500激光干涉仪(LDDM)为测量仪器,图4a)所示立式加工中心被测工作空间行程为800 mm×800 mm×420 mm,图4b)为激光干涉仪测量现场图。在几何误差元素辨识实验中,测量过程严格遵循ISO230-2标准[25],基于改进的“9线法”[26]进行多次测量,辨识得到的各个轴的定位误差、直线度误差和角度误差如图5所示,垂直度误差如表2所示。

图4 测量工作区和测量现场图
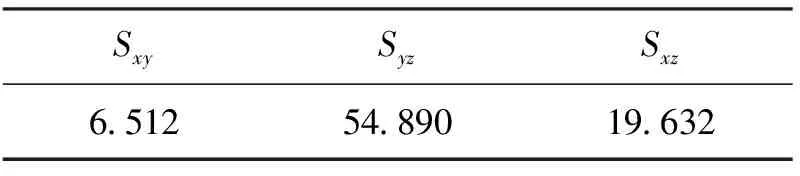
表2 垂直度误差辨识结果 μrad

图5 各个轴位置相关几何误差辨识结果
2.2 立式加工中心几何误差预测
“9线法”测量过程中辨识得到工作空间中3条线3个方向的线性误差,本质上是三轴立式加工心各个轴轴线上的综合线性误差,本文模型可以计算得到各个轴轴线上3个方向误差的预测值,下面对测量值和预测值进行比较来验证模型的正确性。沿各运动轴轴线方向的线性误差的预测值通过综合几何误差POE模型计算得到。由于测量环境中存在的噪声、振动和温度差异等均会影响测量精度,因此测量值除了机床几何误差外,还包含热误差和振动误差等,而通过误差POE模型计算得到的预测值仅包含几何误差,预测值和测量值之间的差异包含了这些因素。因此只要预测值和计算值之间的差异不大(根据实验机床精度,综合考虑各项影响因素后,设定为小于15 μm),则本文模型可视为足够准确。
图6所示为机床沿X轴运动(A0B0线)时3个方向的线性误差和总误差比较图,包含了模型预测值和测量值。从图6中可以看出,x方向的模型计算得到的线性误差预测值与测量值完全一致,y方向的最大偏差(预测值减测量值)为2.26 μm,偏差范围为-0.744~2.26 μm,z方向的偏差范围为-9.68~0.33 μm,总误差的偏差范围为-0.60~4.04 μm。总之,最大偏差不超过15 μm,说明综合几何误差POE模型对X轴的误差预测精度足够高。
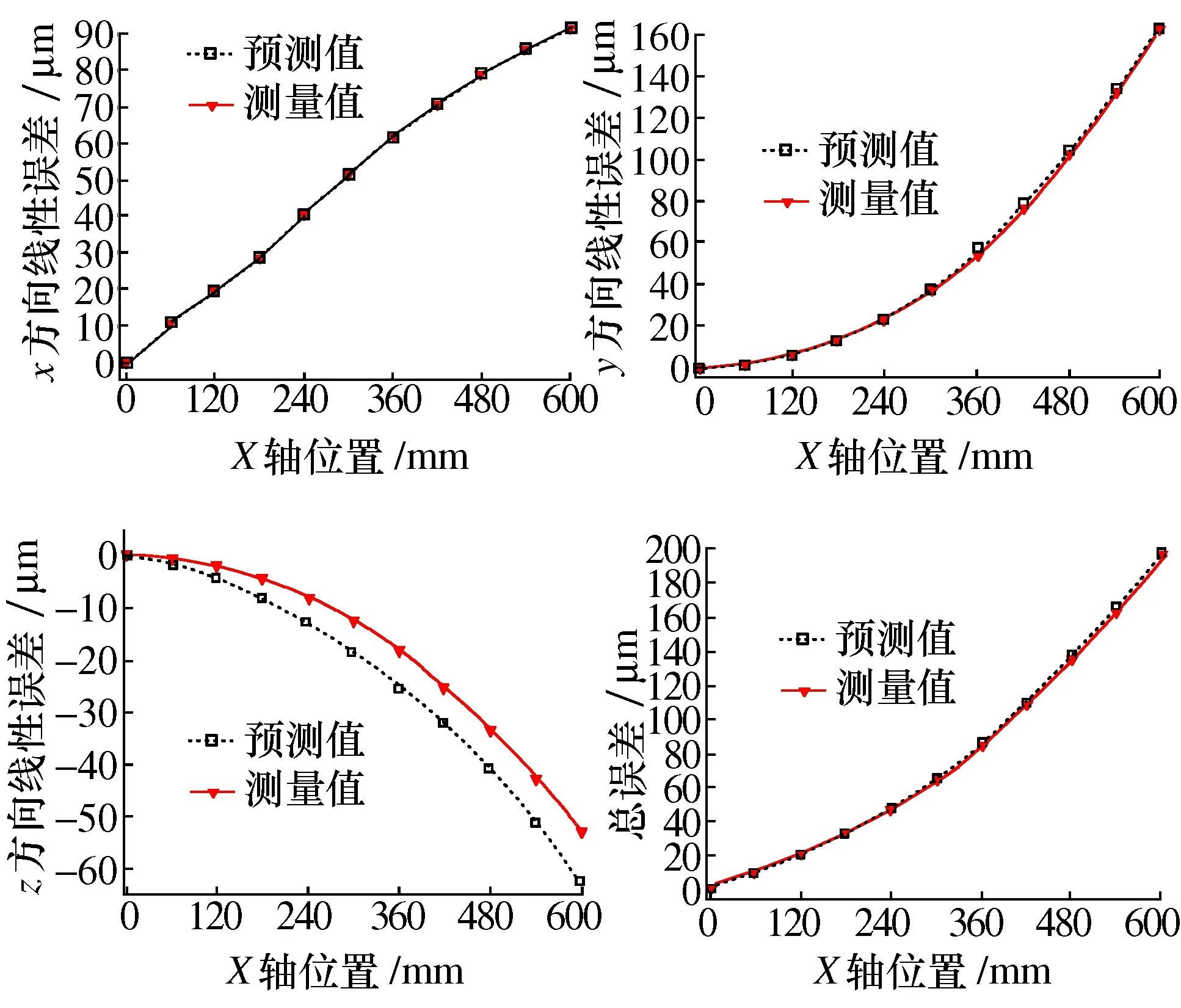
图6 X轴3个方向线性误差和A0B0线的总误差比较图
对于Y轴,即当机床沿A0D0线移动时,最大偏差出现在x方向为13.6 μm。图7所示为3个方向上的预测值和测量值比较图以及Y轴总误差比较图,从图7可知,在y方向上模型预测得出的线性误差与测量值完全一致,z方向的偏差范围为-9~1.7 μm,总误差的偏差范围为-11.3~2.69 μm,最大偏差也小于15 μm,因此综合几何误差POE模型也能够准确预测Y轴的几何误差。

图7 Y轴3个方向线性误差和A0D0线的总误差比较图
图8为机床沿Z轴(A0A1线)移动时线性误差模型预测值与测量值的比较图,从图中可以看出,虽然在x和y方向预测值与测量值的趋势不一致,但最大偏差仅为2.58 μm,而在z方向线性误差预测值和测量值完全相同,总误差的偏差小于2 μm。模型预测结果表明,综合几何误差POE模型也可以精确预测Z轴的几何误差。

图8 Z轴3个方向线性误差和A0A1线的总误差比较图
为进一步验证本文提出的综合几何误差POE模型的有效性,在机床工作区中沿Z轴任意选择一条线(E0E1线),使用LDDM测量机床沿E0E1移动时的线性误差,由于通过LDDM获得的测量值是相对误差,因此第一个测量值必须接近0,为了与预测值进行比较,可以通过更改参考值来调整测量数据。图9所示为机床在3个方向上线性误差的测量值与预测值及总误差比较图,从图9中可以看出,虽然在x方向和y方向上预测值和测量值有所差异,但是偏差很小,其中,x方向的偏差范围为-0.77~14.57 μm,y方向的最大偏差为-6.11 μm,而z方向上预测值和测量值的趋势基本一致,其线性误差的偏差范围为-6.65~1.38 μm,总误差的最大偏差为-6.65 μm,所有的偏差的最大值均小于15 μm。以上结果说明,本文模型在各种情况下均能准确预测三轴立式加工中心的各个轴的几何误差。
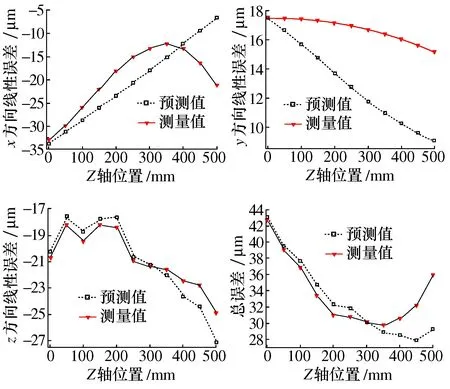
图9 Z轴3个方向线性误差和E0E1线的总误差比较图
从以上实验结果可以看出,本文提出的基于POE旋量理论的综合几何误差POE模型能够准确确预测三轴立式加工中心的几何误差,通过预测结果能够获得机床的几何误差场。图10所示为Z轴的位置误差分布和工作区A0B0C0D0平面的总误差分布,从图10中可以看出,最大位置误差为-70 μm,最大总误差为257 μm。图11所示为整个工作区的误差场分布,包括3个方向的线性误差和总误差,该图呈现出总的几何误差场,可以表示任何点的误差。上述几何误差场分布可应用于后续的机床空间误差补偿。
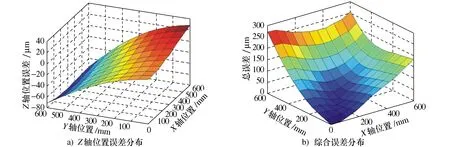
图10 Z轴3个方向的位置误差分布和A0B0C0D0平面的总误差分布
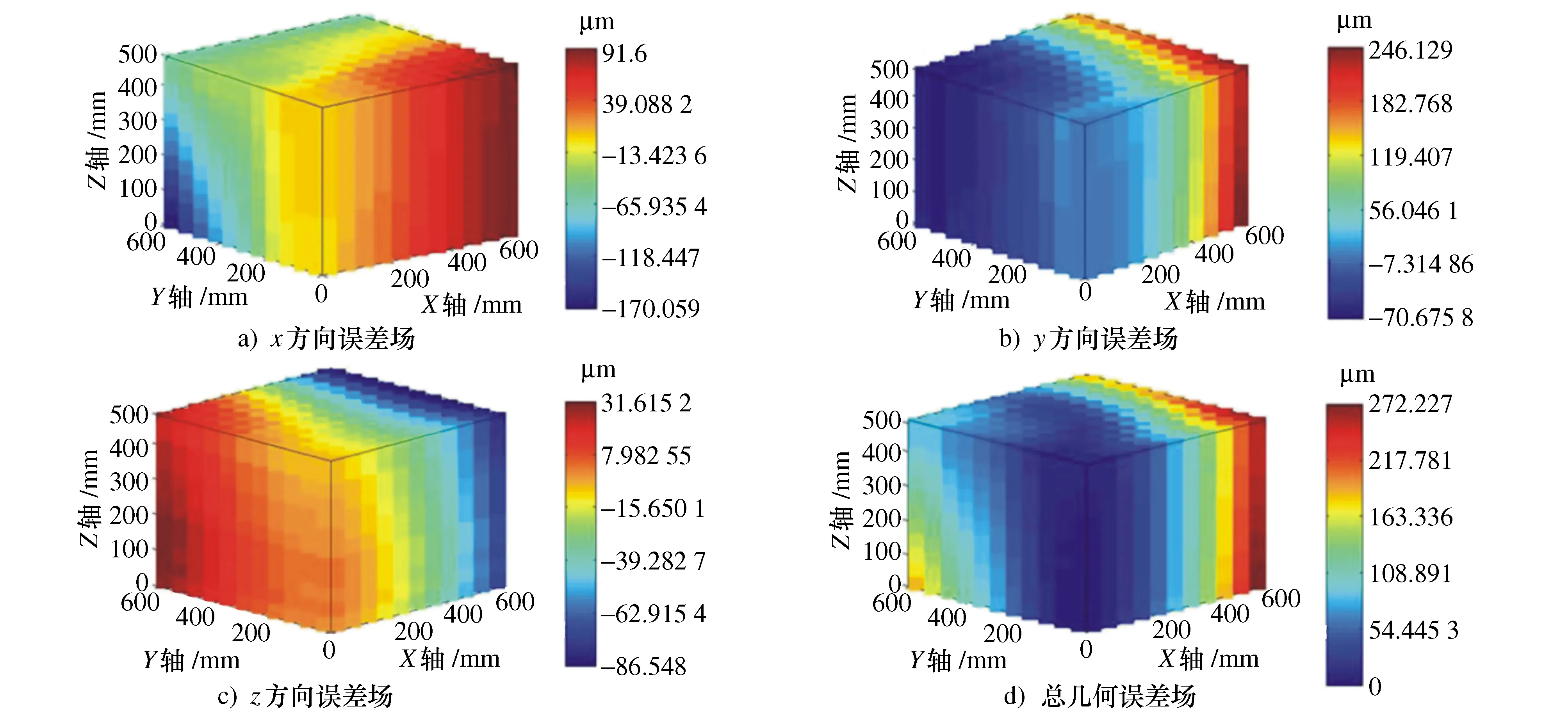
图11 整个工作区的几何误差场
3 结论
1) 针对传统多体系统理论结合HTM方法的几何误差建模过程中局部坐标系构建及齐次坐标变换的繁琐性问题,借助POE旋量理论,面向三轴立式加工中心提出一种较完善的几何误差建模方法。所提方法只需要建立一个基准参考坐标系,并且可以避免矩阵变换的奇异性问题,简化了建模过程。
2) 通过将每个轴的6项基本误差元素分为3组,每组误差元素使用一个旋量来表示,在此基础上构建3个误差POE模型,使得误差POE建模更加简单而准确。
3) 垂直度误差是三轴立式加工中心几何误差元素中的重要组成部分,在误差POE建模时考虑垂直度误差,使得综合误差POE模型更加系统化和精确化。
4) 通过引入基于多体系统理论建立的机床拓扑结构,为综合几何误差POE模型中指数矩阵相乘的次序提供参考,使最终建立的综合POE模型更加合理和易于理解。
