变工况下滚动轴承的故障特征提取

2022-03-15李书乐马洁

机械科学与技术 2022年1期

李书乐，马洁

(1. 北京信息科技大学自动化学院，北京 100192；2. 北京信息科技大学机电学院，北京 100192)

滚动轴承是机械设备中的重要部件,也是极易出现故障的部件。由于振动信号易于监测和包含特征信息丰富等优点,70%的故障诊断都是通过振动分析实现的[1-2],短时傅里叶变换、小波分析和经验模式分解等传统的时频分析方法可以有效地处理振动信号,如唐广先等[3]用基于短时傅里叶变换等方法对滚动轴承进行故障诊断。李恒等[4]提出的基于短时傅里叶变换和卷积神经网络的故障诊断方法实现了端到端的故障模式识别。郑勇[5]用基于小波和能量特征提取的方法进行旋转机械故障诊断。张琛等[6]实现了基于小波包时延相关解调的滚动轴承故障诊断。Chhaya G等[7]用基于经验模态分解和Hjorth参数的方法进行滚动轴承故障诊断。

2014年Dragomiretskiy和Zosso提出了一种新的时频分析方法——变分模态分解(Variational mode decomposition,VMD),克服了传统时频分析方法和经验模态分解等自适应信号分解方法的缺陷,广泛应用于故障诊断领域,如张俊等[8]用基于PSO-VMD-MCKD的方法对风机轴承进行故障诊断。

然而,这些基于振动测试的滚动轴承故障诊断是在假设转速恒定的条件下进行的,实际环境中的滚动轴承通常是在变转速工况下运行的,在设备的启、停过程,电机电压不稳定,转子负载变化时都会引起滚动轴承转速的波动,故其故障振动信号为时变非平稳信号,其故障特征频率是变化的,而现有的时频分析方法在分析时变多分量信号时存在模态混叠现象,不能有效处理这类信号,再加上在实际运行环境中故障源产生强大背景噪声的同时,其他的机械设备也会产生环境噪声,所以故障信号极易淹没在噪声中,而传统的故障诊断方法往往会造成漏诊断现象,本文应用基于广义变分模态分解(GVMD)和分数阶傅里叶变换(FRFT)的方法处理时变非平稳信号,实现对变转速工况下滚动轴承故障的精细诊断。

1 广义变分模态分解

1.1 广义解调

广义解调是一种新型的信号处理工具,尤其适用于多分量非平稳信号的分离。广义解调的核心在于对信号进行广义傅里叶变换,将呈曲线分布的时频特性曲线转换为平行于时间轴的直线,从而避免信号分量在时频域的重叠[9]。

对于信号s(t),其广义傅里叶变换定义为

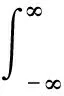
(1)

式中：d(t)为一个实值函数,exp[-j2πd(t)]为核函数。式(1)等同于对s(t)exp[-j2πd(t)]进行标准傅里叶变换,同理定义逆广义傅里叶变换为

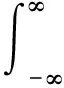
(2)

由此可得,如果令SG(f)=δ(f-f0),则有s(t)=exp{j2π[f0t+d(t)]},所以,假设一个时频分布为f0+d′(t)的信号s(t),只要找到一个近似d(t)的相位函数对原始信号进行广义解调,得到的解调函数s(t)exp[-j2πd(t)]的时频分布将是一条平行于时间轴的直线f(t)=f0。

1.2 变分模态分解

变分模态分解(VMD)是自适应求解约束变分问题的方法,通过循环迭代来求解不同的频率中心及带宽,实现对信号分解[10]。

VMD是一个含约束的最优化问题

(3)

式中：δ(t)为脉冲函数;uk(t)为分解得到的k个本征模态函数(IMF)分量;ωk为第k个分量的中心频率;f为原始信号。

为了求解上述的变分问题,引入拉格朗日算子λ(t)和二次惩罚因子α,把约束优化问题转化为无约束优化问题,其表达式为

(4)

通过乘法算子交替方向法(Alternate direction method of multipliers, ADMM)交替更新的求解过程如下:

2) 循环条件n=n+1;

3) 满足ω≥0时,更新uk；

(5)

4) 更新ωk(t)；

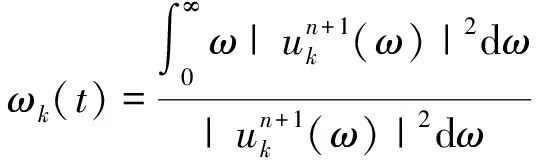
(6)

5) 更新λ；

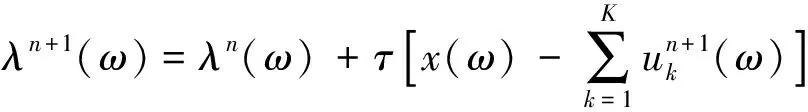
(7)

式中τ为噪声的容限参数。

6) 循环步骤2)～步骤5),直到满足迭代条件(式(8))时停止迭代。

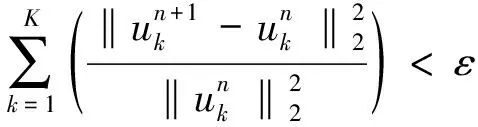
(8)

1.3 广义变分模态分解算法流程

广义变分模态分解是通过将时频特性呈曲线变化的故障特征信号转化为时频特性近似线性变化的信号以实现变转速下轴承的故障诊断,适用于时变多分量信号的处理,具体步骤如下[11]:

1) 通过小波变换预估计信号x(t)中包含的模态个数K。

2) 对实信号x(t)进行希尔伯特变换,得到解析信号y(t)=x(t)+jH[x(t)],j为虚数单位。

3) 对实信号x(t)进行希尔伯特黄变换,求得信号的相位函数dk(t),k=1,2,…,K。

4) 选取步骤3)中冲击性最强分量的相位函数dk(t),对y(t)进行广义傅里叶变换,即Z(t)=y(t)·exp[-j2πdk(t)]。

2 分数阶傅里叶变换

2.1 基于分数阶傅里叶变换的滤波原理

滚动轴承的故障特征频率是非平稳信号,且实际工况下,常常伴随强噪声信号的干扰,分数阶傅里叶变换(FRFT)是处理非平稳信号的有效方法,是一种将信号从时域变换到分数阶域的精细滤波方法,由于非平稳信号在某个分数阶域具有能量聚集的特性,表现出明显的峰值,而噪声信号不具备该特性且其能量会均匀分布在任何的分数阶域上,故只要选择好合适的阶次,就能实现精细地滤波。如文献[12]将分数阶傅里叶变换应用在轴承的故障诊断中。

定义在u′域的函数f(u′)的p阶分数阶Fourier[13]是

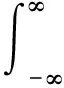
(9)

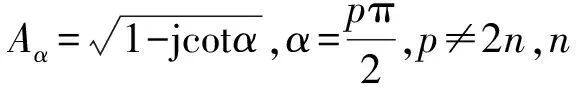
如图1所示,非平稳信号的一个分量的时频分布与时间轴的夹角为β,对该分量进行分数阶傅里叶变换,当其旋转角度α与β正交时,在u0点处则会表现为一个冲击函数,而噪声信号将均匀地分布在整个时域平面。以分数阶域聚焦点u0为中心做窄带滤波,再做FRFT逆变换就可以得到滤波后的时域信号。

图1 FRFT提取信号分量的物理意义图

由图1可以得出,最佳的旋转角度α、阶数p与调频率fm的关系为

(10)

2.2 分数阶傅里叶变换的滤波算法

FRFT对含有噪声的信号滤波过程一般是建立在二维搜索基础上的,通过自由参数的变换改变旋转角度α,在二维平面(α,u)中进行二维搜索得到参数的估计值[14]。计算步骤如下:

1) 对故障信号采用离散采样法FRFT,通过峰值搜索的方法得到最大值对应的α0和u0;

2) 对信号进行p0(p0=2α0/π)阶分数阶傅里叶变换,经过变换所得到的信号为

Xp0(u)=Fp0(u)+Np0(u)

(11)

3) 在u域对形成的尖峰进行遮隔处理,得

(12)

该理想带通滤波器以u0为滤波中心,选择合适的带宽即可滤除掉大部分噪声。

4) 对滤波后的信号进分数阶傅里叶逆变换,得到了消除噪声的信号。

3 仿真信号分析

3.1 GVMD仿真分析

为了验证GVMD算法可以有效处理时变多模态的信号,对复合信号x(t)=x1(t)+x2(t)+x3(t)进行GVMD,其中：

x1(t)=3.5exp(-t)cos[2π(16t3-4t2+25t)] (13)

x2(t)=4cos[2π(22t3-8t2+50t)]

(14)

x3(t)=(3+2t)cos[2π(23t3-12t2+80t)]

(15)

t∈[0,1],其时域波形如图2所示。

图2 x(t)及3个成分的时域波形

首先,对原始信号进行小波变换确定其预分解模态个数,变换后的时频图如图3所示。

图3 小波变换时频图

由图3可清晰的看出原始信号被分解为3个分量,即K=3,这与所给仿真信号的分量个数相符,说明了小波变换可以用来确定预分解模态的个数。首先,对原始信号进行希尔伯特黄变换得到相位函数,选取冲击性最强分量的相位函数d(t)=22t3-10t2对解析信号进行广义傅里叶变换。其次,对广义傅里叶变换后的信号进行VMD分解,惩罚因子a=2 000,分解后信号的时域图如图4a)所示。由此可以看出分解后的分量c1、c2、c3分别对应于真实分量x1(t)、x2(t)、x3(t),虚线为真实分量。再次,为了对比GVMD算法的有效性,采用VMD算法对x(t)进行处理,其分解结果如图4b)所示。

图4 x(t)的2种分解结果

因此,由图4可以看出,GVMD算法的分解结果与真实分量非常接近,证明该算法可以有效地处理包含时变多模态的信号,而VMD算法并不适用。

3.2 FRFT仿真分析

为了验证FRFT算法可以有效降低其他分量和噪声的干扰,对带噪声的仿真信号x(t)=2exp(jπkt2+j2πft)+n(t)进行FRFT滤波。初始频率f为8 Hz,调频率k为8 Hz,采样点数N为1 025,采样频率fs为512 Hz,n(t)为高斯白噪声,信噪比为-15 dB,仿真信号的时域图如图5所示。分数阶傅里叶变换采用采样型算法[15]进行分析,从p=0开始,以p=0.01为步长,得到以p为x轴,以采样点数u为y轴,以FRFT幅值为z轴的分数阶傅里叶域谱,如图6所示,由图可以看出在p=1.02处出现了峰值,峰值为73.77,再以u=529为中心滤波,对滤波后的信号逆变换得到的信号时域图如图7所示,与图3仿真信号的时域图对比可知FRFT有良好的的滤波效果。

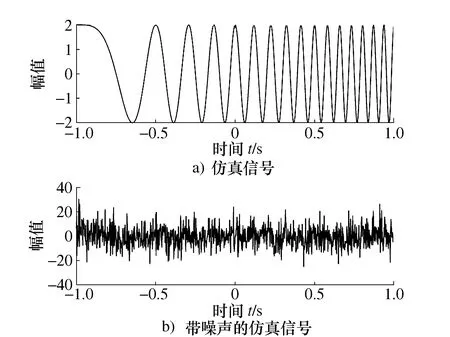
图5 仿真信号时域图

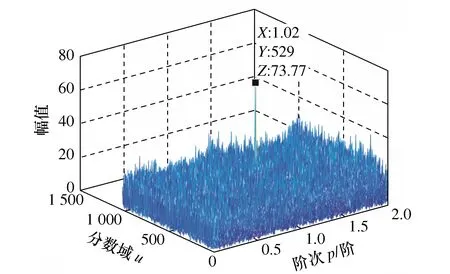
图6 分数阶傅里叶变换后的故障诊断分析图

图7 滤波后信号的时域图

4 变转速工况下滚动轴承故障特征提取的试验验证

4.1 试验数据介绍

在本节中,将用试验采集到的故障数据证明该方法的有效性。试验数据来自渥太华大学实验室的旋转机械故障模拟器MKF-PK5M。试验台如图8所示[16],主轴由一个交流逆变器控制的电动机驱动,两端分别由两个轴承支撑。两个轴承中间装有负载,故障轴承位于左侧。在试验台上安装转速计和加速度计,分别采集轴转速和振动信号。数据经信号调节器(PCB PIEZOTRONIC 482C15)处理后,送入NI数据采集模块(NI USB-6212 BNC),由计算机软件Labview记录。本文采用转速从1 092 r/min变化至2 100 r/min时的滚动轴承内圈故障数据,表1所示为所用轴承的具体参数情况。

图8 旋转机械故障试验台

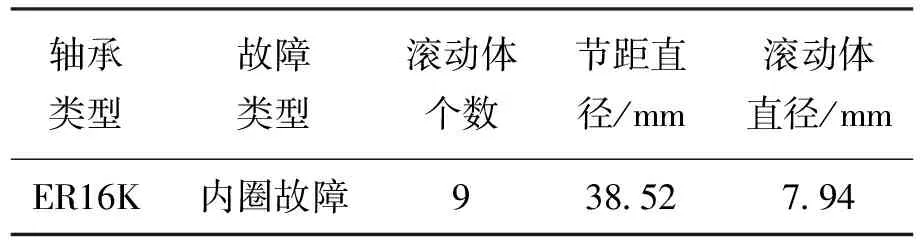
表1 内圈故障轴承参数

4.2 GVMD-FRFT滚动轴承故障特征提取算法

本文所提出的 GVMD-FRFT算法不仅可以有效地抑制噪声干扰,而且可以解决变工况情况下信号处理困难的问题,能有效地对信号进行分离,提取包含故障特征最完整的信号分量,再通过对该分量的包络分析提取出故障特征频率,滚动轴承故障特征提取的具体操作流程如图9所示。

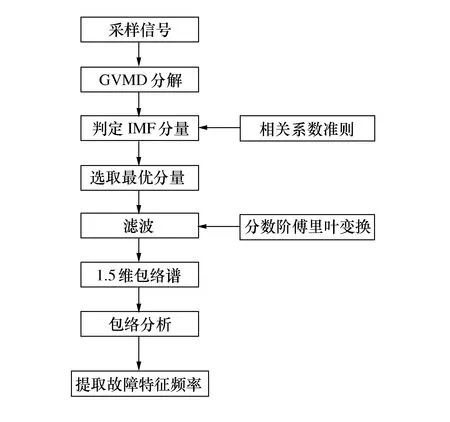
图9 滚动轴承特征提取流程图

4.3 滚动轴承内圈故障信号分析

选取滚动轴承内圈故障数据进行GVMD分解,通过对原始数据进行小波变换得到预分解分量个数,小波变换后的时频图如图10所示,虽然小波变换得到的时频谱分辨率低,但可以看出原始信号包含了4个单分量,故K=4。对数据进行希尔伯特黄变换得到相位函数,选取冲击性最强分量的相位函数d(t)=47 540t+51对解析信号进行广义傅里叶变换,再对变换后的信号进行VMD分解。原始故障信号的时域图如图11所示,GVMD分解后的分量如图12与图13所示。

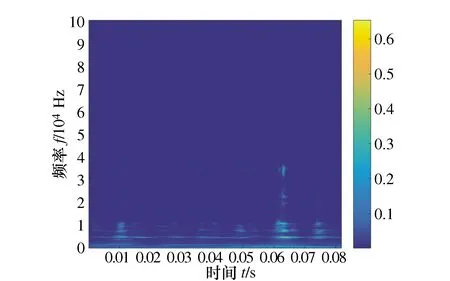
图10 小波变换时频图

图11 滚动轴承内圈故障数据时域图

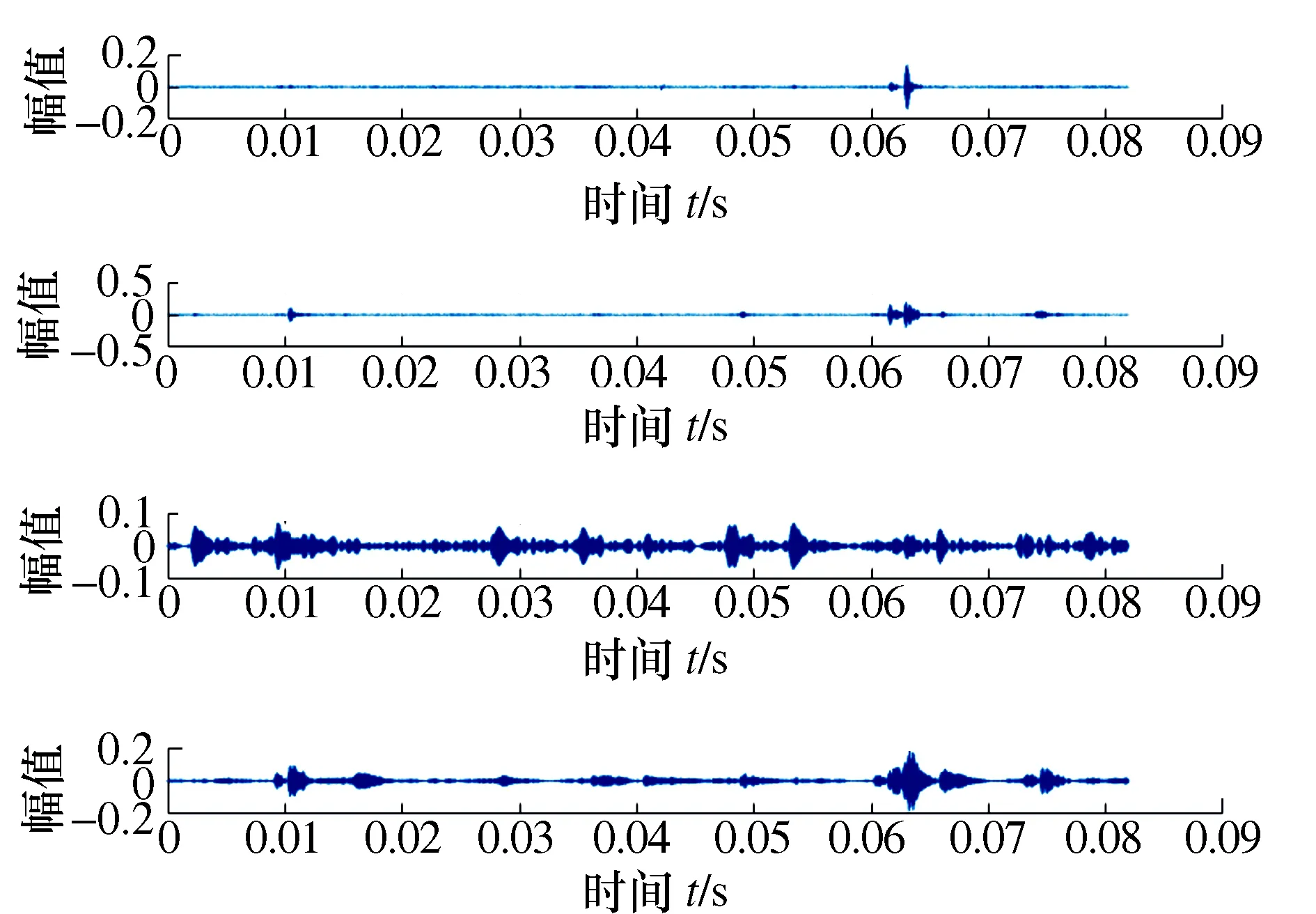
图12 GVMD分解后各分量时域图

图13 GVMD分解后各分量频谱图

由相关系数法则可知,相关系数越大的分量与原始信号的故障特征越接近,分解后得到各IMF分量的相关系数如表2所示。

表2 IMF分量的相关系数

由表2可知,IMF1的相关系数最大,因此,选用IMF1作为下一步分析的目标信号。

令p∈[1.4,1.6],以Δp=0.001为步长,利用离散采样法FRFT算法可得到分数阶傅里叶变换结果如图14所示,利用峰值搜索方法可得出峰值,即p=1.452,u0=9 416,故可设计滤波器为Mp(u)=[zeros(1,u0-1),ones(1,1),zeros(16384-u0)],该滤波器仅允许u0处的信号通过。

图14 分数阶傅里叶变换后的结果图

含噪声信号的分数域与幅值波形如图15所示,经过分数阶域滤波后信号的分数域与幅值波形如图16所示,由此可以明显看出,滤波前的信号包含很多噪声干扰,而滤波后的信号无噪声干扰,这说明FRFT实现了对信号的降噪处理。

图15 含噪声的故障振动信号分数域与幅值关系

图16 滤波后信号的分数域与幅值关系

最后,对该信号做分数阶傅里叶逆变换,得到如图17所示的时域波形图。

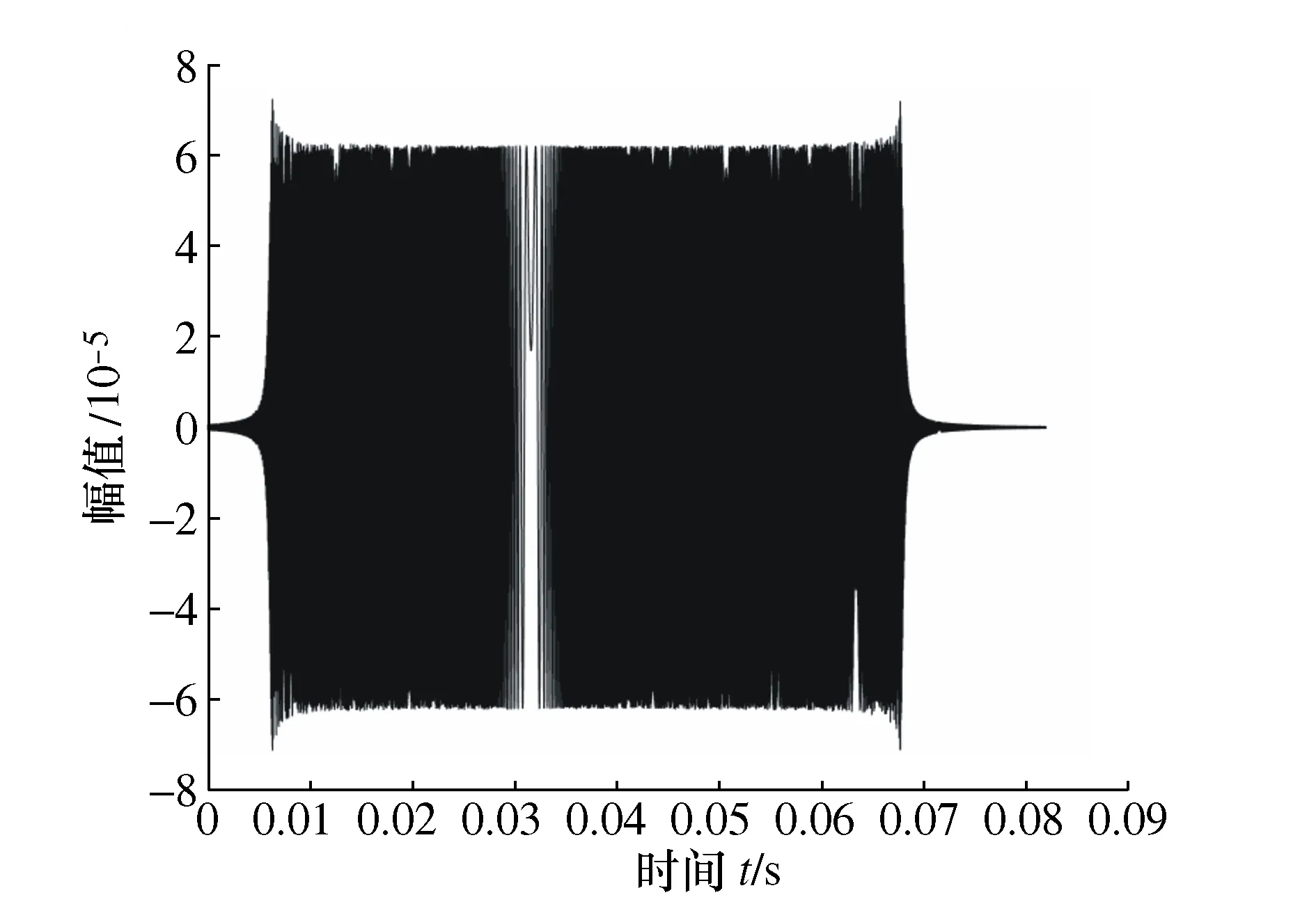
图17 滤波后的信号时域图

滤波后对故障的时域信号进行1.5维包络解调如图18所示,故障频率值为122.1 Hz。所用实验数据采集时间很短,持续了5.46 s,转速从1 092 r/min变化至2 100 r/min,波动范围很小,故以1 350 r/min为参考标准计算得出的理论故障频率值为122.1 Hz,与实际值保持一致,成功地提取出了故障特征频率。