测定动摩擦因数实验题赏析

卞晓娟 高爱虎 褚加星 刘立毅(正高级教师)

(1.山东省德州市第一中学 2.山东省平原县第一中学)

动摩擦因数是描述接触面粗糙程度的物理量，既可以根据公式直接测算，也可以根据物理规律设计实验方案间接测量.下面从动摩擦因数的测量原理和所用器材等角度进行归纳.

1 根据摩擦力公式，采用打点计时器法

1.1 实验器材与装置

利用木块、一端带定滑轮的长木板、打点计时器、纸带、砝码、槽码、细线等器材安装成图1所示装置.

1.2 实验原理

图1中木块沿水平面滑动时，摩擦力Ff＝μFN＝μMg，可根据得出μ;也可多次实验测得多组(Ff，M)值作出Ff-M图像，由图像斜率得到动摩擦因数μ.

例1(2021 年江苏新高考适应性考试)用图1所示的实验装置测量木块与长木板间的动摩擦因数μ.把左端带有滑轮的长木板平放在实验桌上，载有砝码的木块右端连接穿过打点计时器的纸带，左端连接细线，细线绕过定滑轮挂有槽码，木块在槽码的牵引下运动.通过纸带测量木块的加速度，并测出木块与砝码的总质量M，槽码的总质量m，计算木块与木板之间的摩擦力Ff，改变M和m进行多次实验.

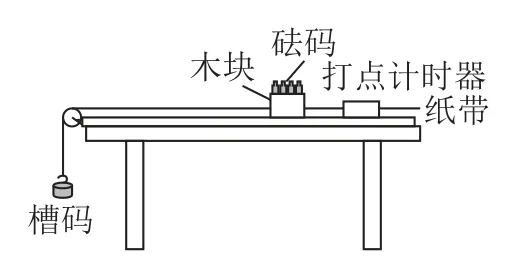
图1

(1)下列实验操作步骤的正确顺序是_________;

①释放木块

②接通打点计时器电源

③将木板固定在水平桌面上

④调节滑轮高度使细线与木板平行

⑤纸带穿过打点计时器限位孔并固定在木块上

(2)实验打出的一段纸带如图2所示，打点计时器的工作频率为50Hz，图中纸带按实际尺寸画出，则木块的加速度为____m·s－2;(保留2位有效数字)

图2

(3)甲同学测得的数据见表1.请根据表中的数据，在方格纸上作出Ff-M图像;

表1

(4)已知重力加速度g取9.80 m·s－2，可求得该木块与木板的动摩擦因数μ＝_______;

(5)乙同学用(3)问表1中的数据逐一计算出每次测量的μ值，取其平均值作为测量结果，他发现该值比甲同学在(4)问中得出的μ值大.你认为哪位同学的结果更准确，请简要说明理由_____________.

(1)正确顺序是③⑤④②①.

(2)如图3所示，每4个点选为一个计数点，则计数周期T＝0.08s.由图3可知xOC＝3.90cm，xOE＝9.00cm，由逐差法得

图3

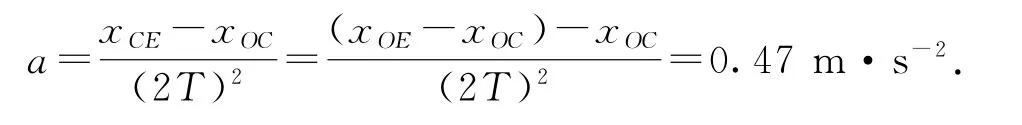
(3)将表中数据拟合成直线，如图4所示.

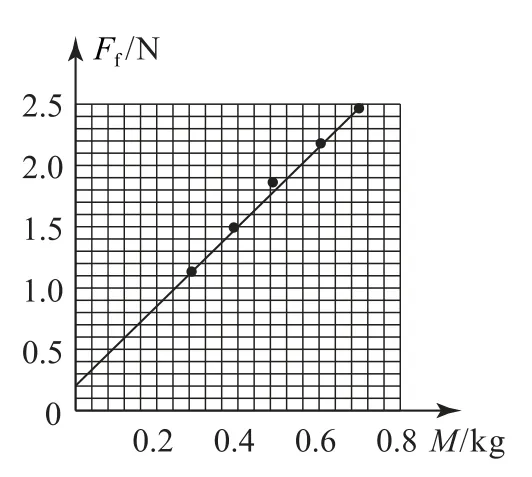
图4

(4)由滑动摩擦力公式得Ff＝μg·M，可知Ff-M图像的斜率为μg，则，解得μ＝0.33.

(5)甲同学用图像法，拟合直线时让更多的点在图线上，偏离直线较远的点可以舍弃.乙同学通过求平均值无法做到这一点，因此甲同学的结果更准确.

第(2)问正确选择计数点、计数周期和加速度的表达式是基础和关键点.第(5)问甲、乙同学测量值大小关系，除解析中提到的原因外，还可以作科学推理和论证如下:系统运动过程，实际所受摩擦力Ff＝μMg＋F′f(纸带和限位孔间摩擦力、打点阻力、空气阻力)大于理论值μMg，所以乙算出的μ偏大，此为系统误差.Ff-M图像中的斜率与F′f无关，所以甲得到μ为准确值，无系统误差，此为图像法的优点.

2 根据平衡条件和牛顿运动定律，采用倾斜轨道摄像法

2.1 实验器材与装置

利用手机、一端带定滑轮的长木板、垫块、物块(质量为M)、刻度尺、钩码(质量为m)、细线等器材，安装成图5所示装置.

2.2 实验原理

图5 中连接体匀速运动时，有Mgsinα＝μMgcosα＋mg.烧断细线后，利用手机多次拍摄物块匀加速运动的视频，作出图像，根据图像求出其加速度a，对物块由牛顿第二定律有MgsinαμMgcosα＝Ma，联立可求得动摩擦因数μ.

图5

例2某同学设计了如下实验来测量物块与木板之间的动摩擦因数，实验步骤如下:

①如图5所示，用垫块把一端带有定滑轮的长木板垫高，在其上表面固定一与物块下滑路径平行的刻度尺(图中未画出).物块用细线通过定滑轮与一质量为m＝100g的钩码相连.

②实验发现当木板的倾角调整为53°时，给物块一个沿斜面向下的初速度，物块恰能拖着钩码匀速运动.

③调整手机使其摄像头正对木板表面，开启视频录像功能.当物块运动到某一位置时突然烧断细线，用手机记录下物块沿木板向下做加速直线运动的情况.然后通过录像的回放，选择烧断细线时物块的位置作为测量参考点，得到物块相对于该点的运动距离L与运动时间t的数据.

图6

回答以下问题:(重力加速度g取9.80m·s－2，sin53°＝0.8，cos53°＝0.6)

(1)根据图像可得，烧断细线瞬间物块速度的大小为_________m·s－1，物块下滑的加速度大小为_________m·s－2;(结果均保留2位有效数字)

(2)根据上述数据，可得物块的质量为_________kg，物块与木板间的动摩擦因数为________.(结果均保留2位有效数字)

(1)烧断细线后，小车做初速度为v0的匀加速直线运动，有，可得，结合图像得v0＝0.20m·s－1，＝k＝2.05 m·s－2，则加速度a＝2k＝4.1m·s－2.

(2)设物块质量为M，斜面倾角α＝53°，连接体匀速运动，由平衡方程有Mgsinα＝μMgcosα＋mg.剪断细绳后，对物块由牛顿第二定律有MgsinαμMgcosα＝Ma，联立得mg＝Ma，解得.

本题创新实验手段，用手机的录像功能记录物块加速运动情况，并结合平衡条件和牛顿第二定律计算动摩擦因数.第(1)问，烧断细线后，对物块根据位移公式列出方程后，应进行线性化处理，将其转化为的形式，从而与图像转译，利用斜率和截距，求得初速度和加速度.第(2)问烧断细线前后，需要分别列出木块匀速、匀加速运动的方程，联立才可求出动摩擦因数.

3 根据牛顿第二定律，采用水平光电门法

3.1 实验器材与装置

利用滑块、一端带定滑轮的木板、光电门、遮光条、拉力传感器、重物、细线等器材，安装成图7所示装置.

图7

3.2 实验原理

根据遮光条宽度d，通过光电门时间t，算出其通过光电门的速度v.已知滑块运动的距离L，根据v2＝2aL计算出其加速度a.根据牛顿第二定律，对滑块及其上器材有F－μmg＝ma，求出a.改变滑块质量或重物质量多次实验测得多组值，画出图像.根据图像的斜率、截距即可得到动摩擦因数μ.

例3某中学兴趣研究小组为了测量滑块与木板之间的动摩擦因数设计了以下的实验如图7所示.木板放置在水平桌面上，木板的右端固定一定滑轮，木板的左端放置有一滑块，滑块上固定有一遮光条，其宽度为d，在木板上B点固定一光电门，滑块初始位置A到B点的距离为L.一根细线一端连接重物，另一端绕过滑块右侧的定滑轮与最右端的拉力传感器相连，使细线保持水平，重力加速度为g.实验步骤如下:

A.将滑块从A点由静止释放，传感器示数为F，光电门记录遮光条通过光电门的时间t;

B.改变重物质量重复步骤A;

C.正确记录每一组F与t对应的数据，作出的关系图像如图8所示(图中b、c为已知量).

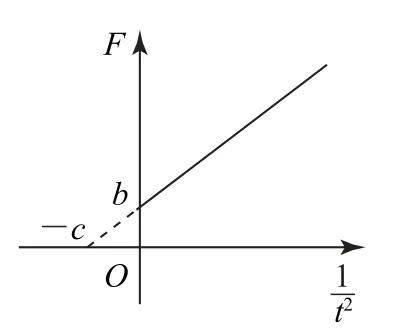
图8

(1)根据题干已知物理量和步骤A 中测出的物理量可知，滑块的加速度a＝________;

(2)已测得滑块(含遮光片、定滑轮)质量为m，则滑块与轨道间的动摩擦因数μ＝________;

(1)滑块在拉力作用下做匀加速运动，到达光电门B时速率为;

(2)对滑块根据牛顿第二定律有2F－μmg＝ma，联立步骤(1)中的表达式有;

(3)当改变滑块质量时，其加速度也将变化，列出其表达式为，所以有图像是一条直线，结合图像斜率和截距有.那么当m增大时，b变大，c不变.

在本实验中，滑块受到的拉力可以通过力传感器直接得到，更直接更准确.第(3)问应形成数形合一的思维模式，需将根据牛顿第二定律所列方程转化为的形式，再与所给的图像转译，寻找函数方程和图像的斜率、截距的关系进行求解.此法称为函数图像法.

4 根据动能定理，采用刻度尺测量法

4.1 实验器材与装置

利用刻度尺、小物块、表面粗糙的斜面和水平面、铅垂线等器材，安装成图9所示装置.

4.2 实验原理

如图9所示，设斜面倾角为θ，小物块沿斜面从A滑到C后静止，此过程中，由动能定理得mgh＋WFf＝0－0，其 中WFf＝－μmgcosθ·xAB－μmgxBC，两式联立可求动摩擦因数μ.

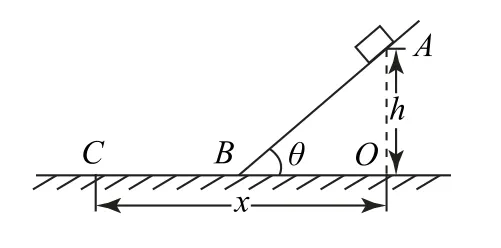
图9

例4用刻度尺等器材可以测量动摩擦因数.实验装置如图9所示，表面粗糙程度相同的斜面和水平面在B处平滑连接，实验步骤如下:

①将一小物块从斜面上的某一点(记为A)由静止释放，物块滑到水平面上的某一点(记为C)停下;

②用铅垂线测定A点在水平面的投影点O，用刻度尺测量AO的高度h、OC的长度x;

③改变释放点的位置，重复上述步骤，记录多组关于hn、xn的数据.

请回答下列问题:

(1)用测得的数据(hn、xn)表示，物块与水平面间的动摩擦因数为_________;

(2)步骤③可以避免测量动摩擦因数的________(填“偶然”或“系统”)误差;

(3)根据测得的数据画出图10 图像，最合理的是_________;

图10

(4)实验中，小物块从斜面上的A1点由静止释放，运动到水平面上的C1点停止，A1点在水平面的投影为O1，记录下O1C1的长度x1;增大斜面倾角，再将小物块从A2点由静止释放，运动到水平面上的C2点停止，A2点与A1点等高，A2点在水平面的投影为O2，记录下O2C2的长度x2，则x1_______x2(填“＞”“＝”或“＜”);小物块从A1到C1的过程记为“Ⅰ”，从A2到C2的过程记为“Ⅱ”，在同一坐标系中画出小物块速率v随时间变化的图像，如图11所示，正确的是_________.

图11

(1)设斜面的倾角为θ，物块滑到斜面底端B点时的速度为v，物块从A滑到B的过程，由动能定理得，从B滑到C的过程，由动能定理得－μmgxBC＝，两式联立解得.

(2)步骤③改变释放点的位置，重复上述步骤，是为了避免偶然误差.

(3)从A到C的全过程，由动能定理得mghμmgcosθ·xAB－μmgxBC＝0，整理得h＝μx，故h-x图像为正比例函数，选丁.

(4)两次全过程由动能定理得mgh－μmgx＝0，因为两次释放点的高度相同，故x1＝x2.在Ⅰ和Ⅱ两个过程中，在斜面上的运动阶段由动能定理得mgh－，故斜面倾角越大，到达底端的速度越大.在斜面上运动过程中，由牛顿第二定律有mgsinθ－μmgcosθ＝ma，得a＝gsinθ－μgcosθ，因为θ2＞θ1，故a2＞a1，在水平面上减速运动的加速度均为a＝μg，此段v-t图像应该平行，故选B.

本题从能量观念设计实验，方法巧妙，器材简洁，易于操作.第(1)问构建粗糙斜面模型并得出滑动摩擦力做功结论:WFf＝－μmgx水平(x水平为斜面的水平位移)，为应用动能定理奠定基础.第(2)问，由实验原理不完善产生的误差为系统误差，本实验应多次测量，从而减小实验产生的偶然误差.第(4)问，弄清题中x1和x2是释放点和停止点的水平位移，而非斜面的水平位移，是正确求解的关键.

(完)