深度剖析粒子流背景类试题

徐华兵

(浙江省金华第一中学)

高中物理中常常出现以气体流、液体流、粒子流和不能看成质点的绳子等为背景的试题，这类试题也被统称作粒子流背景类试题.这类试题背景常取材于生活实际，能很好地考查高中物理力学主干知识.而解决这类问题需要学生合理选取研究对象，构建物理模型——柱体模型，能很好地考查学生模型建构、科学推理等关键能力，深受命题者的青睐.

笔者在讲授粒子流背景类试题时发现，很多学生在用动量定理和动能定理两种不同的方法求解时，结果有细微差别，学生感觉两种方法求解都是正确的，而结果却不同，甚是疑惑，甚至怀疑动量定理和动能定理解决粒子流背景类试题方法的自洽性，本文拟对此进行深入剖析.

1 粒子流背景类试题

由于粒子流分布在整个空间，所以处理粒子流背景类试题时研究对象的选取尤为重要，解题中常采用微元思想建立“柱体模型”，选取任意Δt时间段内的“粒子流”为研究对象.笔者根据粒子流是否运动将粒子流背景类试题分为两类——静止粒子流背景类试题和运动粒子流背景类试题.

1.1 静止粒子流背景类试题

静止粒子流是指粒子流均匀静止分布在空间中，即粒子流的初速度为零.当外界物体进入粒子流空间中时，与粒子流发生相互作用.由于外界物体对粒子流有力的作用，粒子流由静止开始运动，动量、能量发生变化.

例1宇宙飞船在飞行过程中有很多技术问题需要解决，其中之一就是当飞船进入宇宙微粒尘区时如何保持速度不变的问题.假设一宇宙飞船以速度v进入密度为ρ的微粒尘区，飞船垂直于运动方向上的最大截面积为S.且认为微粒与飞船相碰后都附着在飞船上，则飞船要保持速度v不变，所需推力为多大?

分析与求解宇宙飞船在前进空间区域中遇到微粒尘区，微粒尘埃吸附在宇宙飞船上.被吸附在飞船上的微粒尘埃具有和宇宙飞船相同的速度.沿宇宙飞船运动方向建立“柱体模型”(如图1).任取一极小时间段Δt，则在此Δt时间段内有体积为S·v·Δt柱体内的微粒尘埃吸附在宇宙飞船上.要求解微粒尘埃与宇宙飞船间的作用力F，可选取极小段时间内与宇宙飞船发生相互作用的微粒尘埃柱体作为研究对象，应用动量定理或动能定理求解.

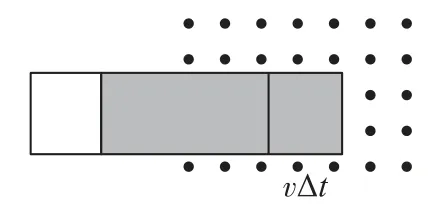
图1

方法1动量定理法

Δt时间段内有体积为S·v·Δt柱体内的微粒尘埃吸附在宇宙飞船上，其对应的质量Δm＝ρ·S·v·Δt，对极小段柱体内的微粒尘埃应用动量定理有F·Δt＝Δm·v＝ρ·S·v·Δt·v，解得F＝ρSv2.

方法2动能定理法

Δt时间内有体积为S·v·Δt的微粒尘埃由初速度为0变为速度v，所以Δt时间内，此柱体内的微粒尘埃位移为.对微粒尘埃应用动能定理有v2，将位移Δx值代入即得F＝ρSv2.

很多学生从动能定理角度求解作用力F时，误认为在微小时间段Δt内柱体内的微粒尘埃发生的位移Δx＝v·Δt，从而利用动能定理F·计算出的作用力为，与应用动量定理法求解的作用力F相差一个系数.此种解法忽略了微粒尘埃与宇宙飞船相互作用时所发生的相对运动，微粒尘埃的速度从0变为v，而宇宙飞船一直匀速直线运动，所以存在相对位移.进一步分析知Δt时间内微粒尘埃与宇宙飞船的相对位移x相＝，宇宙飞船与微粒尘埃因相互作用而损失的机械能，即产生的热量Q＝F·x相＝.

变式汽车高速行驶时，空气阻力不能忽略，将汽车简化为横截面积约为1 m2的长方体，并以此模型估算汽车以60km·h－1行驶时为克服空气阻力所增加的功率.已知空气密度ρ＝1.3kg·m－3.

分析与求解已知汽车的运行速度，要求解汽车因克服空气阻力所增加的功率，可先利用动量定理求出汽车与空气(粒子流连续体)之间的作用力，再利用功率计算式P＝F·v计算因克服空气阻力所增加的功率.也可从能量守恒角度分析，先计算极小段时间Δt内空气(粒子流连续体)获得的动能Ek和汽车与空气(粒子流连续体)相互作用所产生的热能Q(或系统损失的机械能)，再利用公式计算所增加的功率.

方法1动量定理法

Δt时间内有体积为S·v·Δt柱体内的空气粒子流与汽车发生相互作用，其对应的空气粒子流质量Δm＝ρ·S·v·Δt，对极小段空气粒子流柱体应用动量定理有F·Δt＝Δm·v，解得F＝ρSv2.克服空气阻力所增加功率P＝F·v＝ρSv3＝6019 W.

方法2能量法

Δt时间内有体积为S·v·Δt柱体内的空气与汽车发生相互作用，其对应的质量Δm＝ρ·S·v·Δt，空气柱获得的动能

空气粒子流速度从0增加到与汽车相同的速度v，空气粒子流与汽车间因相对运动产生热量Q ＝Ek＝，增加的功率ρSv3＝6019 W.

汽车与静止的空气粒子流相互作用，空气粒子流与汽车之间发生相对滑动，有能量损失，且损失的能量刚好等于空气粒子流获得的动能.

1.2 运动粒子流背景类试题

运动粒子流是指粒子流以某一固定速度在空间中运动.当外界物体进入运动粒子流所处空间时，由于外界物体速度与运动粒子流速度不同，故外界物体与运动粒子流间有力的作用.

例2一艘帆船在静水中由于风力的推动做匀速直线运动，帆面的面积为S，风速为v1，船速为v2(v2＜v1)，空气密度为ρ，帆船在匀速前进时帆面受到的平均风力大小为多少? (设空气碰到帆后随帆一起运动)

分析与求解帆船在运动的同时，空气粒子流也在运动，由于空气粒子流的速度比船向前运动的速度大，所以空气粒子流对船帆面有沿运动方向力的作用，此作用力为帆船前进的动力.若取前进的帆船作为参考系，则空气粒子流相对帆船的初速度v0＝v1－v2，空气粒子流与帆船作用后的速度为0.利用微元法建立柱体模型如图2所示，取一极小时间段Δt，在Δt时间内有ΔV＝S·(v1－v2)·Δt体积内空气粒子流与帆船发生作用，对应空气粒子流柱体质量Δm＝ρ·S(v1－v2)·Δt.对圆柱体内的空气粒子流柱体应用动量定理有－F·Δt＝0－Δm·(v1－v2)，解得空气粒子流对帆船的作用力F′＝F＝ρS(v1－v2)2.

图2

帆船在运动，空气粒子流也在运动，两个物体都在运动给求解带来了麻烦，若取前进中的帆船为参考系，那么在该参考系中帆船可看作不动，空气粒子流相对于帆船运动，规律较为简单.

变式一帆船在静水中顺风飘行，风速为v0，求船速多大时，风供给帆船的功率最大? (设帆船帆面是完全弹性面，且与风向垂直，面积为S).

分析与求解空气粒子流(风)在运动，帆船也在运动，两个物体都运动，较为复杂，若取帆船为参考系，则化两个物体运动为一个物体运动，求解较为方便.设帆船行驶速度为v，取帆船为参考系，则风以(v0－v)的初速度撞击帆船并原速率反弹.取一极小时间Δt，则此Δt时间内与帆船发生作用的空气粒子流质量Δm＝ρ·S(v0－v)·Δt.对风柱体应用动量定理有F·Δt＝Δm·2(v0－v)，代入数据得风与帆船间的作用力F＝2ρS(v0－v)2.

地面系中，风对帆船的功率

由于帆船帆面是完全弹性面，所以风与帆船帆面相互作用时为弹性碰撞，无能量损失.极小时间Δt内风(空气粒子流)损失的动能即为帆船获得的能量，故可从能量的角度求解

2 类粒子流——软绳背景类试题

软绳可看作一种特殊的粒子流，运动(或静止)部分质量可以连续变化，具有粒子流的性质，只不过不同段绳与绳之间有力的作用.软绳运动状态的改变需要力的作用，软绳动量、能量会发生变化.根据软绳类粒子流的运动类型不同，可将软绳类粒子流背景类试题分为匀速运动软绳类试题和匀变速运动软绳类试题.

2.1 匀速运动软绳类试题

匀速运动软绳类试题是指软绳在外界力的作用下做匀速运动，由于软绳运动部分质量不断增加，软绳具有的动量、能量不断变化.一般采用微元法求解软绳内部运动段和静止段间的作用力，即选取一段极小时间Δt，则有长度Δl＝v·Δt段软绳运动状态发生改变，可对这一极小段软绳应用动量定理求作用力.

例3如图3 所示，长度为l的柔软绳堆放在光滑的水平面上，其线密度为λ，现用水平力拉绳的一端，使之做速度为v的匀速直线运动.已知t＝0时刻拉出的绳子长度l0＝0，求:

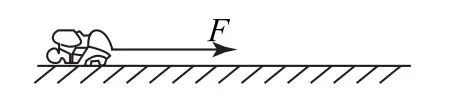
图3

(1)所需的拉力F;

(2)从初始时刻到将整条绳子拉动的过程中，拉力做的功W.

分析与求解(1)在水平拉力F的作用下，软绳沿水平方向展开.任意时刻取极小时间段Δt，由于绳子一端做匀速直线运动，有长度Δl＝v·Δt段绳子由静止变为运动.对这极小段绳子应用动量定理有F·Δt＝Δm·v＝λv·Δt·v－0，解得F＝λv2.

(2)据上述求解知，水平拉力F为恒力，拉力F做的功即为恒力做的功，则有WF＝F·l＝λv2·l.

软绳在拉力F的作用下做匀速运动，运动段软绳的长度、质量不断改变，属于变质量问题.直接对已经运动的软绳不好分析，此时可应用微元法，任取极小时间段Δt，选取即将开始运动的Δl＝v·Δt段软绳作为研究对象进行分析.

变式一段单位长度质量为λ的细绳，绕放在光滑水平面上(不交叉，不重叠)，用力以速度v匀速向上提升绳的一端，如图4 所示.求:当绳被提升高度为y时作用在绳端的作用力有多大?

图4

分析与求解要求解作用在绳端的作用力F，此作用力F的作用效果一部分用来克服已经变为匀速直线运动段绳子的重力，一部分用来克服运动段绳和静止段绳间的冲击力.任取极小段时间Δt，此时间内有Δy＝v·Δt段绳子即将开始运动.对Δy段绳子应用动量定理有F冲·Δt＝Δm·v－0，得F冲＝λv2，对运动段绳分析有F＝F冲＋λy·g＝λv2＋λy·g.

软绳被匀速提起时，拉力F一方面要克服竖直绳的重力，另一方面克服冲击力，用微元法对微小段绳应用动量定理求冲击力大小.本题也可从能量角度求解，由于绳子从水平地面上速度为0变为竖直方向上速度为v，绳子在拉直绷紧过程中有能量损失.

2.2 匀变速运动软绳类试题

匀变速运动软绳类试题是指软绳在外界力的作用下做匀变速直线运动.由于软绳做匀变速直线运动，所以运动段软绳的质量、动量和能量发生变化.求解这类问题时一般也采用微元法，选取运动状态即将发生改变的极小段软绳进行分析.

例4一质量为m、长为l的均匀软绳自由悬垂.下端恰与一台秤秤盘接触，某时刻放开软绳上端，求台秤的最大读数.

分析与求解软绳释放后做自由落体运动，任取t时刻落到秤盘上静止软绳长x，则此时竖直软绳下落的距离为x，速度.软绳对台秤的压力应包括两部分，软绳下落对台秤的冲击力和静止在台秤上的软绳对台秤的压力，如图5所示.利用微元法求冲击力，在任意t时刻取极小时间段Δt，则在此时间段内有质量段绳子从速度v变为0.对此极小段绳子应用动量定理有

图5

用微元法对极小段软绳应用动量定理求冲击力时，由于冲击力远远大于此极小段软绳的重力，故相对冲击力冲量而言，极小段软绳所受重力冲量可忽略不计.

变式如图6所示，利用自动称米机称米，买者认为，因为米落在容器中时有向下的冲力，造成读数偏大，因而不划算.卖者认为，当读数满足需要时，自动装置立即切断米流，尚有一些米在空中，这些米都是多给买者的.请问自动称米机到底准不准?

图6

分析与求解自动称米机到底准不准关键取决于切断开关时米流对台秤的冲击力大小与空中米流重力的大小关系，若米流对台秤冲击力大小与空中米流重力大小相等，则自动称米机准，否则不准.利用微元法选取一段极小时间Δt，则Δt时间内落入台秤的米流质量Δm＝m0·Δt，m0为单位时间从自动称米机流出的米的质量.对此极小段米流应用动量定理有－F·Δt＝0－Δm·v，解得米流对台秤冲击力F＝;空中米流重力

经分析知米流对台秤冲击力与空中米流重力刚好相等，所以自动称米机是准确的.

来自自动称米机的米流可以看作类匀变速运动软绳类粒子流.求解米流对台秤的冲击力时，仍可采用求解软绳内冲击力的方法.

以粒子流为背景的试题由于能很好地考查高中物理力学部分动量定理和动能定理知识而深受命题者的青睐.准确求解这类试题要求学生能从抽象的物理情境中建立物理模型.一般先用微元思想，选取一段极小时间，建立一个微小的“柱体模型”，再对已建立的柱体模型应用动力学规律求解.

(完)