On Mixed Pressure-Velocity Regularity Criteria to the Navier-stokes Equations in Lorentz Spaces,Part II:The Non-slip Boundary Value Problem∗
2022-03-14HugoBEIRODAVEIGAJiaqiYANG
Hugo BEIRO DA VEIGA Jiaqi YANG
1Department of Mathematics,Pisa University,Pisa,Italy.E-mail:hbeiraodaveiga@gmail.com
2School of Mathematics and Statistics,Northwestern Polytechnical University,Xi’an 710129,China.E-mail:yjqmath@163.com yjqmath@nwpu.edu.cn
Abstract This paper is a continuation of the authors recent work[Beir˜ao da Veiga,H.and Yang,J.,On mixed pressure-velocity regularity criteria to the Navier-Stokes equations in Lorentz spaces, Chin.Ann.Math.,42(1),2021,1–16],in which mixed pressure-velocity criteria in Lorentz spaces for Leray-Hopf weak solutions of the three-dimensional Navier-Stokes equations,in the whole space and in the periodic torus ,are established.The purpose of the present work is to extend the result of mentioned above to smooth,bounded domains Ω,under the non-slip boundary condition.Let π denote the fluid pressure and v the fluid velocity.It is shown that ifwhere 0 ≤θ ≤1,andwith p ≥2,then v is regular on Ω×(0,T].
Keywords Navier-Stokes equations,Pressure-speed links,Regularity criteria,Lorentz spaces,Boundary value problem
1 Introduction:The Main Result
We are concerned with the regularity of weak solutions to the Navier-Stokes equations
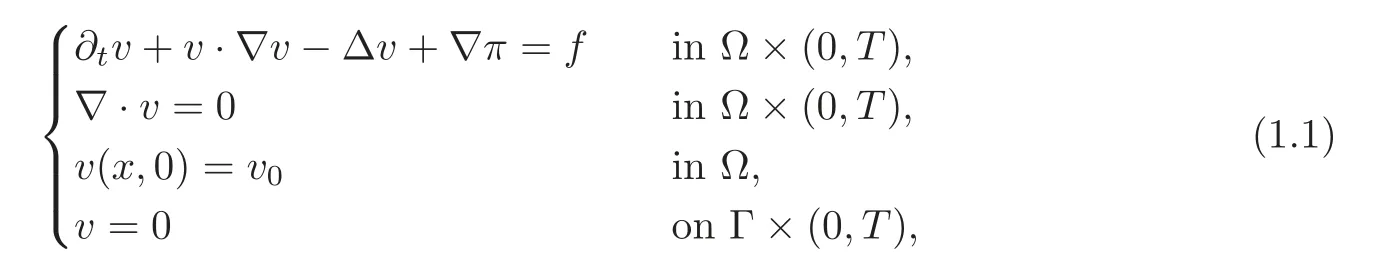
wherevis the flow velocity field,πis the pressure,and the initial datav0is divergence free.Ω is a smooth open,bounded,subset ofand Γ denotes its boundary.fis an external force.Throughout the whole paper we assume,without loss of generality,that for almost allt∈(0,T),the pressureπhas vanishing mean-value in Ω.
In our recent paper[6],we established new integral criteria for regularity of weak solutions to the Navier-Stokes equations.These criteria generalize the classical,well-known,Ladyzhenskaya-Prodi-Serrin(L-P-S for short)criteria,see the pioneering references[17],[21],[23].Let’s briefly recall these criteria.They established,in their stronger,more recent form,that if a weak solutionvof(1.1)satisfies





2 Auxiliary Results



3 Proof of Theorem 1.2



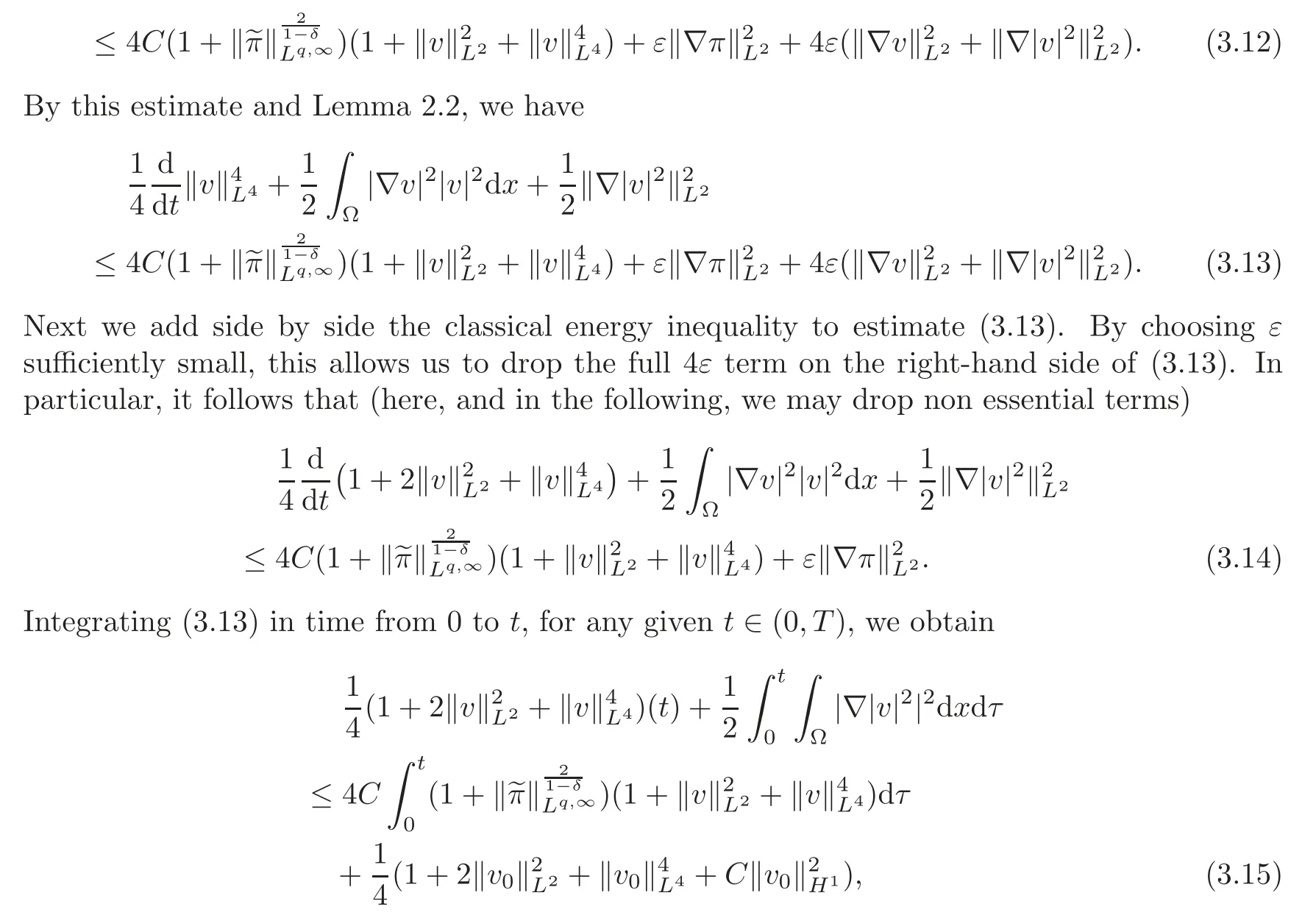

杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Local Unstable Entropy and Local Unstable Pressure for Partially Hyperbolic Endomorphisms∗
- Diophantine Inequality by Unlike Powers of Primes
- The Isoperimetric Inequality in Steady Ricci Solitons∗
- Pythagorean Theorem &Curvature with Lower or Upper Bound∗
- Spreading Speeds of Time-Dependent Partially Degenerate Reaction-Diffusion Systems∗
- Range-Renewal Processes:SLLNs and Power Laws∗
