The Isoperimetric Inequality in Steady Ricci Solitons∗

Yuqiao LI

1Department of Mathematics,University of Science and Technology of China,Hefei 230026,China.E-mail:lyq112@mail.ustc.edu.cn

Abstract The author proves that the isoperimetric inequality on the graphic curves over circle or hyperplanes over Sn−1 is satisfied in the cigar steady soliton and in the Bryant steady soliton.Since both of them are Riemannian manifolds with warped product metric,the author utilize the result of Guan-Li-Wang to get his conclusion.For the sake of the soliton structure,the author believes that the geometric restrictions for manifolds in which the isoperimetric inequality holds are naturally satisfied for steady Ricci solitons.

Keywords Isoperimetric inequality,Ricci soliton

1 Introduction and Statement of the Main Results

2 The Isoperimetric Inequality in Riemannian Manifolds with Warped Product Metric

3 Cigar Steady Soliton

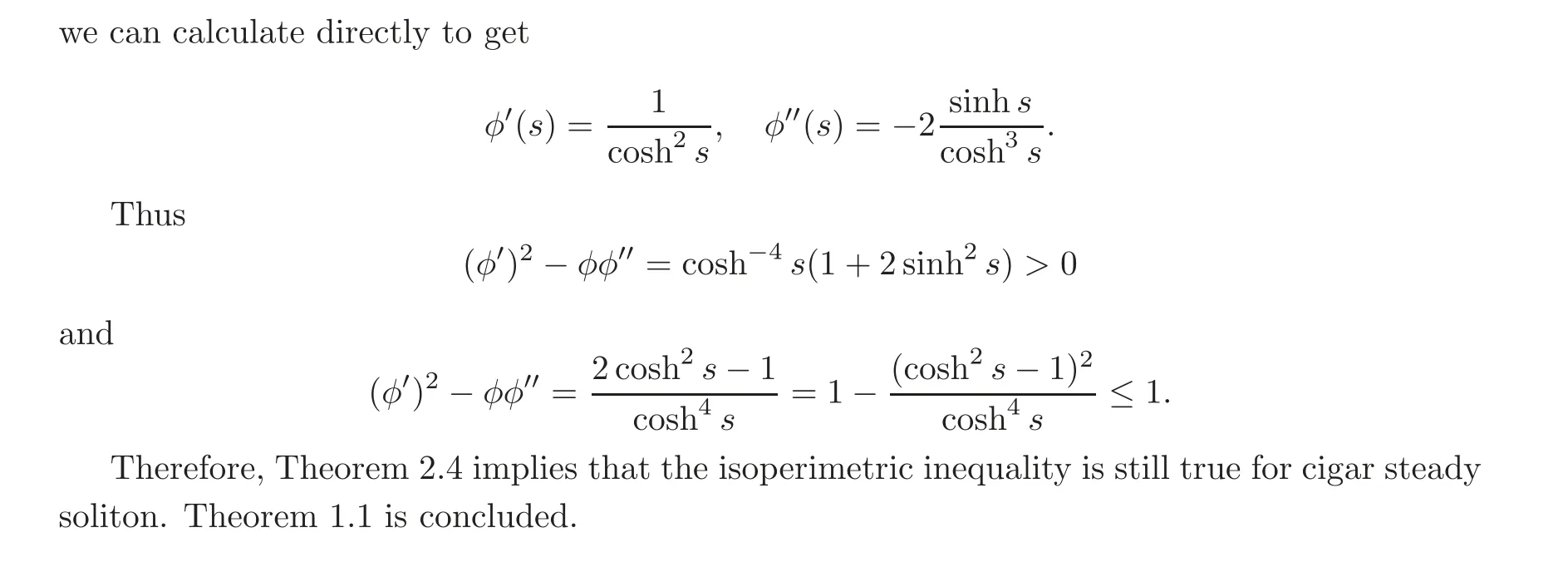
4 Bryant Steady Soliton

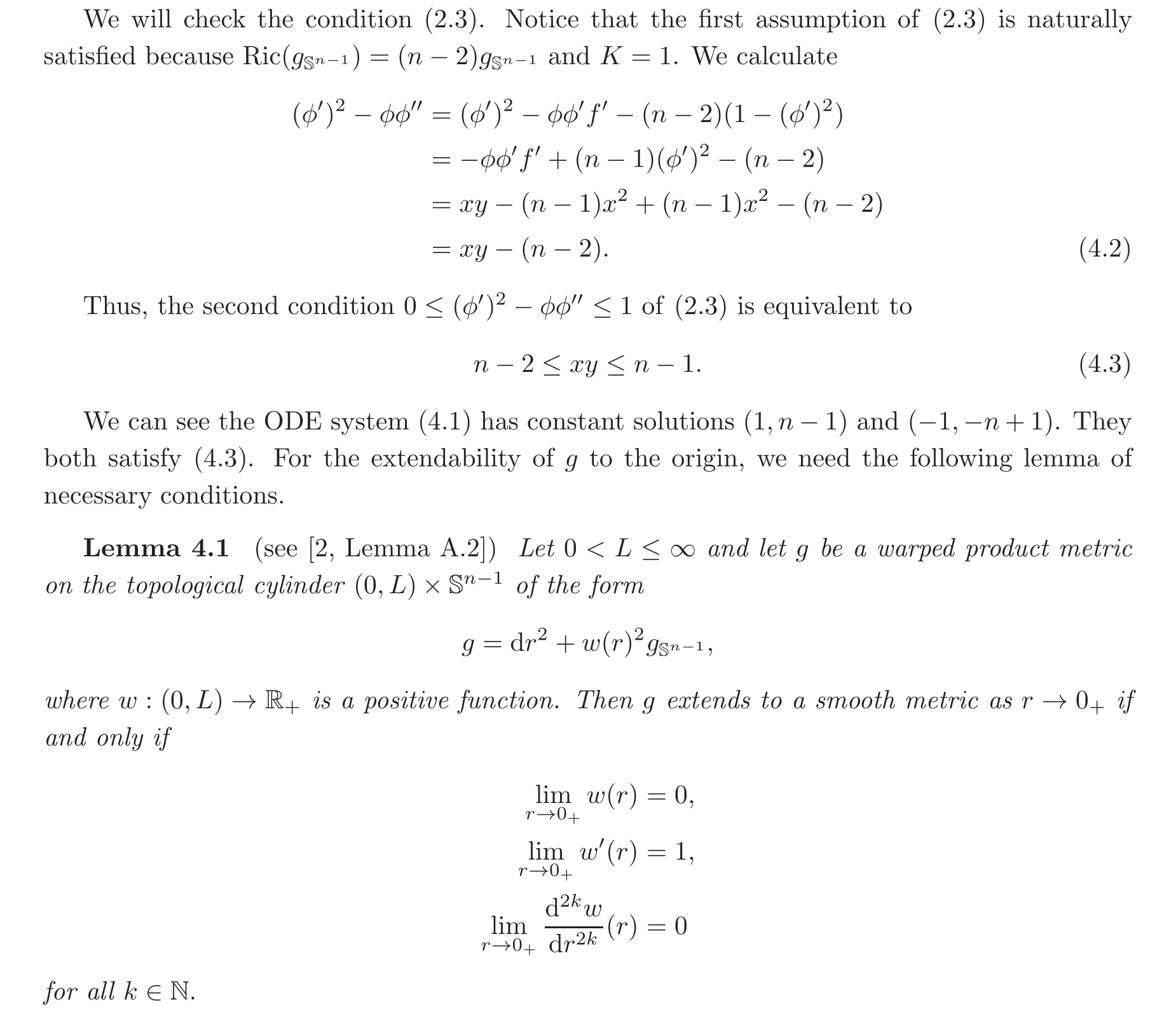
AcknowledgementI would like to express my gratitude to my advisor Professor Jiayu Li.He introduced me the problem and gave me so much useful suggestions.I also want to thank the anonymous referee for comments that improved this paper.