Pythagorean Theorem &Curvature with Lower or Upper Bound∗

Xiaole SU Hongwei SUN Yusheng WANG

1School of Mathematical Sciences(and Lab.math.Com.Sys.),Beijing Normal University,Beijing,100875,China.E-mail:suxiaole@bnu.edu.cn

2School of Mathematics Science,Capital Normal University,Beijing,100037,China.E-mail:5598@cnu.edu.cn

3Corresponding author.School of Mathematical Sciences(and Lab.math.Com.Sys.),Beijing Normal University,Beijing,100875,China.E-mail:wyusheng@bnu.edu.cn

Abstract In this paper,the authors give a comparison version of Pythagorean theorem to judge the lower or upper bound of the curvature of Alexandrov spaces(including Riemannian manifolds).

Keywords Pythagorean theorem,Alexandrov space,Toponogov’s theorem

1 Introduction

1In this paper,A° denotes the interior part of A.2Refer to Section 2 for the definition of an interior point of a finite dimensional CBB-type Alexandrov space.

2 On Alexandrov Spaces

3 Proof of Theorem A for Curvature ≥(≤)k

In this section,we will show the former part of Theorem A,i.e.,the sufficiency and necessity of the condition for curvature ≥kor ≤kin Theorem A.By Theorems 2.2 and 2.2′,it is enough to verify the sufficiency,and the verification shall be proceeded according to the following cases.

Case 1 For curvature ≥karound a CBB-type pointx∈X.

Case 2 For curvature ≥karound a CBA-type pointx∈X.

Case 3 For curvature ≤karound a CBA-type pointx∈X.

Case 4 For curvature ≤karound a CBB-type pointx∈X.

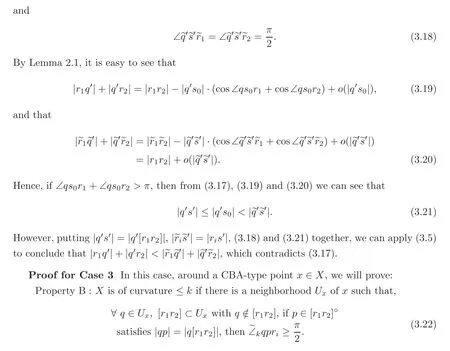
4 Proof of Theorem A for Curvature ≡k on X°

3The metric on CzX is defined from the Law of Cosine on R2 by viewing distances on ΣzX as angles(see[2]).

5 Proofs of Theorem C and Corollary D

So,by Theorem C,xis regular point.