Range-Renewal Processes:SLLNs and Power Laws∗

Xinxing CHEN Jiansheng XIE Jiangang YING

1School of Mathematical Sciences,Shanghai Jiaotong University,Shanghai 200240,China.E-mail:chenxinx@sjtu.edu.cn

2School of Mathematical Sciences,Fudan University,Shanghai 200433,China.E-mail:jsxie@fudan.edu.cn jgying@fudan.edu.cn

Abstract Given n samples(viewed as an n-tuple)of a γ-regular discrete distribution π,in this article the authors concern with the weighted and unweighted graphs induced by the n samples.They first prove a series of SLLN results(of Dvoretzky-Erd¨os’ type).Then they show that the vertex weights of the graphs under investigation obey asymptotically power law distributions with exponent 1+γ.They also give a conjecture that the degrees of unweighted graphs would exhibit asymptotically power law distributions with constant exponent 2.This exponent is obviously independent of the parameter γ ∈(0,1),which is a surprise to us at first sight.

Keywords Range renewal process,Strong law of large numbers,Power law

1 Introduction

2 Main Settings and Main Results

2.1 Main settings

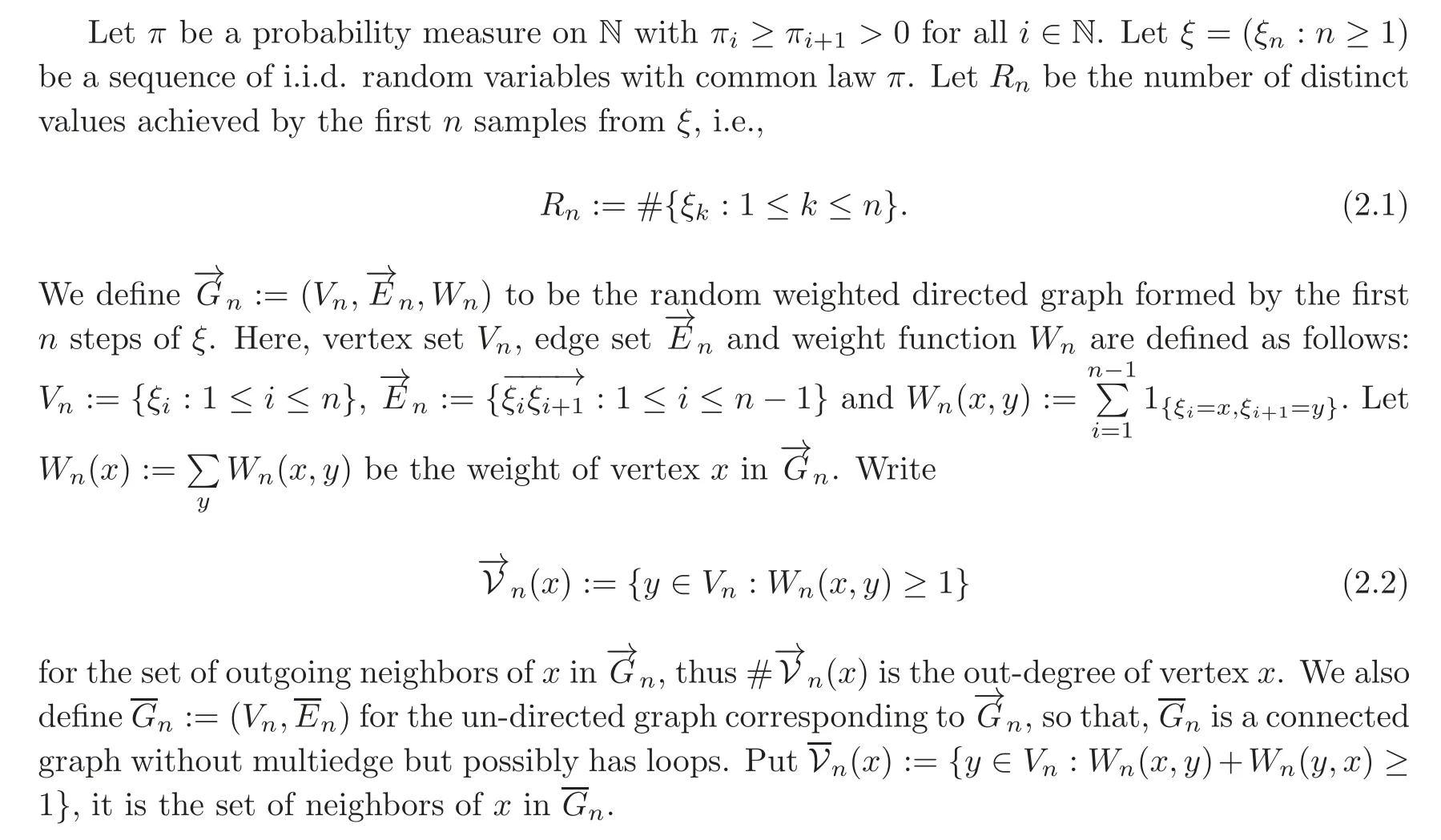
2.2 Main results

3 Preliminary Estimates

3.1 Expectation-variance estimate for Rn

3.2 Expectation estimates for visit intensity statistics

3.3 Variance estimates for visit intensity statistics

3.4 Estimates for out-degree statistics

4 Proofs for the Main Theorems 2.1–2.4

5 Discussions

5.1 0-Regular case:γ(π)=0

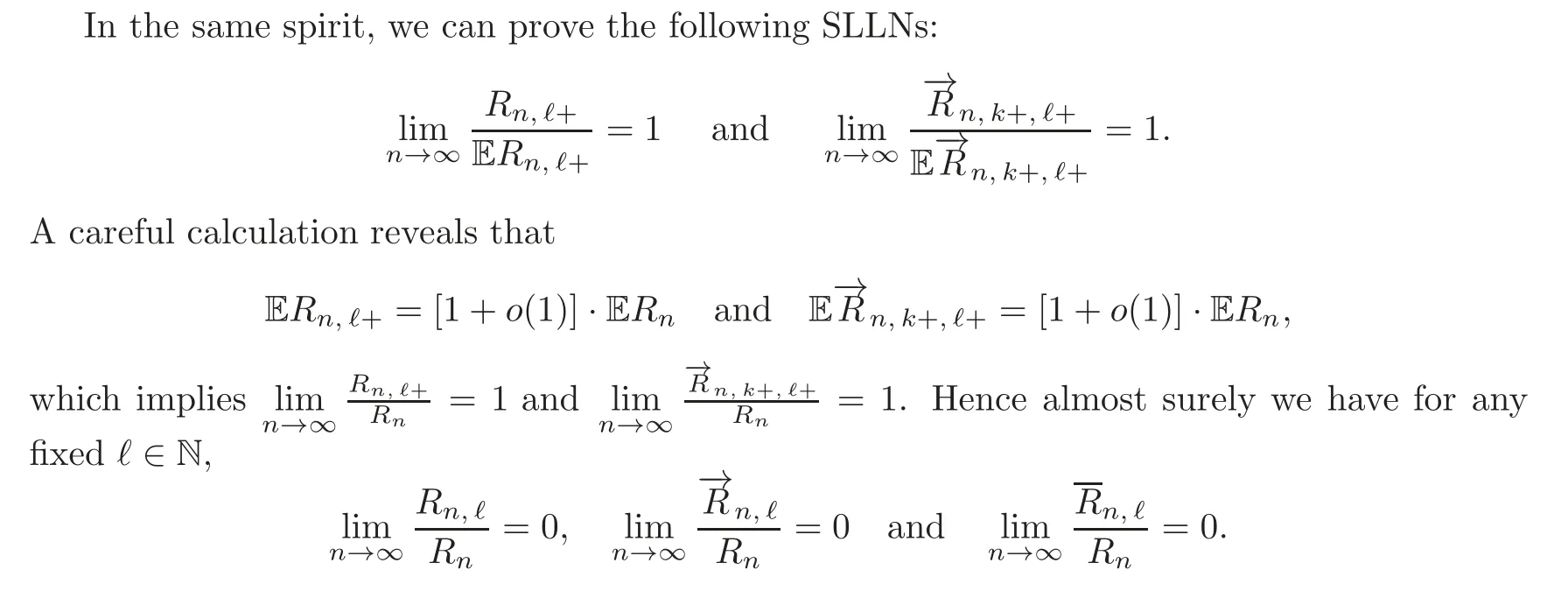
5.2 1-Regular case:γ(π)=1

5.3 A conjecture

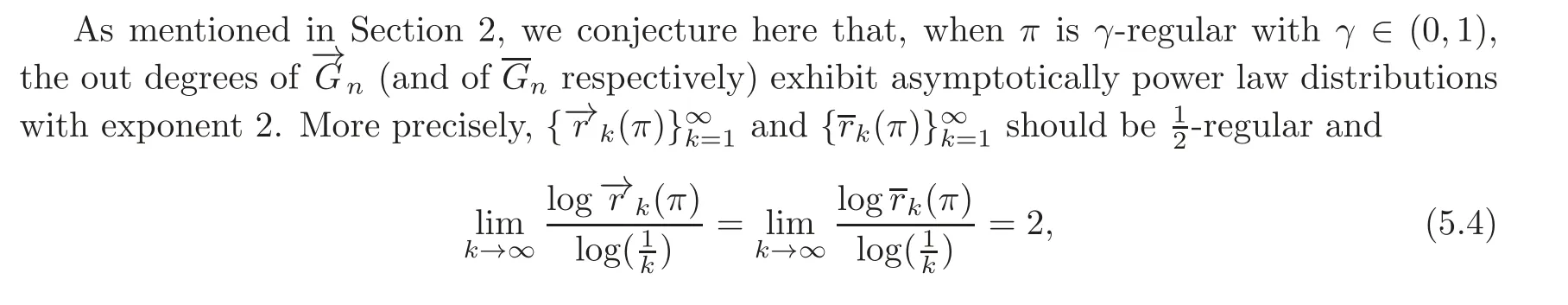
AcknowledgementsWe are in debt to the anonymous referee for his valuable suggestions which make the current version of our manuscript more readable.The second author would like to thank Prof.De-Jun Feng and his colleagues Professors Yi-Jun Yao and Yun-Xin Zhang for helpful discussions and comments.He also expresses the gratitude to Prof.Derriennic for sending him a copy of[11].