Orbifold Stiefel-Whitney Classes of Real Orbifold Vector Bundles over Right-Angled Coxeter Complexes∗

Lisu WU

School of Mathematical Sciences,Fudan University,Shanghai 200433,China.E-mail:wulisuwulisu@qq.com

Abstract The author gives a definition of orbifold Stiefel-Whitney classes of real orbifold vector bundles over special q-CW complexes(i.e.,right-angled Coxeter complexes).Similarly to ordinary Stiefel-Whitney classes,orbifold Stiefel-Whitney classes here also satisfy the associated axiomatic properties.

Keywords Right-Angled Coxeter orbifold,Stiefel-Whitney class,Group representation

1 Introduction

The definition of characteristic classes of an orbifold vector bundle depends on the cohomology ring of its base space(an orbifold).The de Rham cohomology groups of an orbifold are introduced by Satake[15],so one can define orbifold chern classes of a good complex orbifold vector bundle by Chern-Weil construction,which take values in de Rham cohomology groups of base orbifold.Moreover,this definition can be extended to bad orbifold vector bundles(see[17]).

In addition,one can take the equivalent cohomology ring as the cohomology ring of a quotient orbifold.Now the equivalent characteristic classes can be viewed as orbifold characteristic classes.In the book of Adem-Leida-Ruan[1],the orbifold characteristic classes defined lie in the cohomology rings of classifying spaces of the orbifold groupoids.According to[1,Example 2.11],their orbifold characteristic classes actually correspond to the equivalent characteristic classes.

However,the integral and Mod-two integral cohomology rings of general orbifolds are unclear.So it is difficult to define orbifold characteristic classes in the usual way(see[14]).

Recently,L¨u-Wu-Yu[12]introduced integral orbifold cellular homology groups of Coxeter complexes by applying the idea of blow-up.In this paper,we define and study orbifold Stiefel-Whitney classes on right-angled Coxeter complexes based on the cohomology groups of L¨u-Wu-Yu.

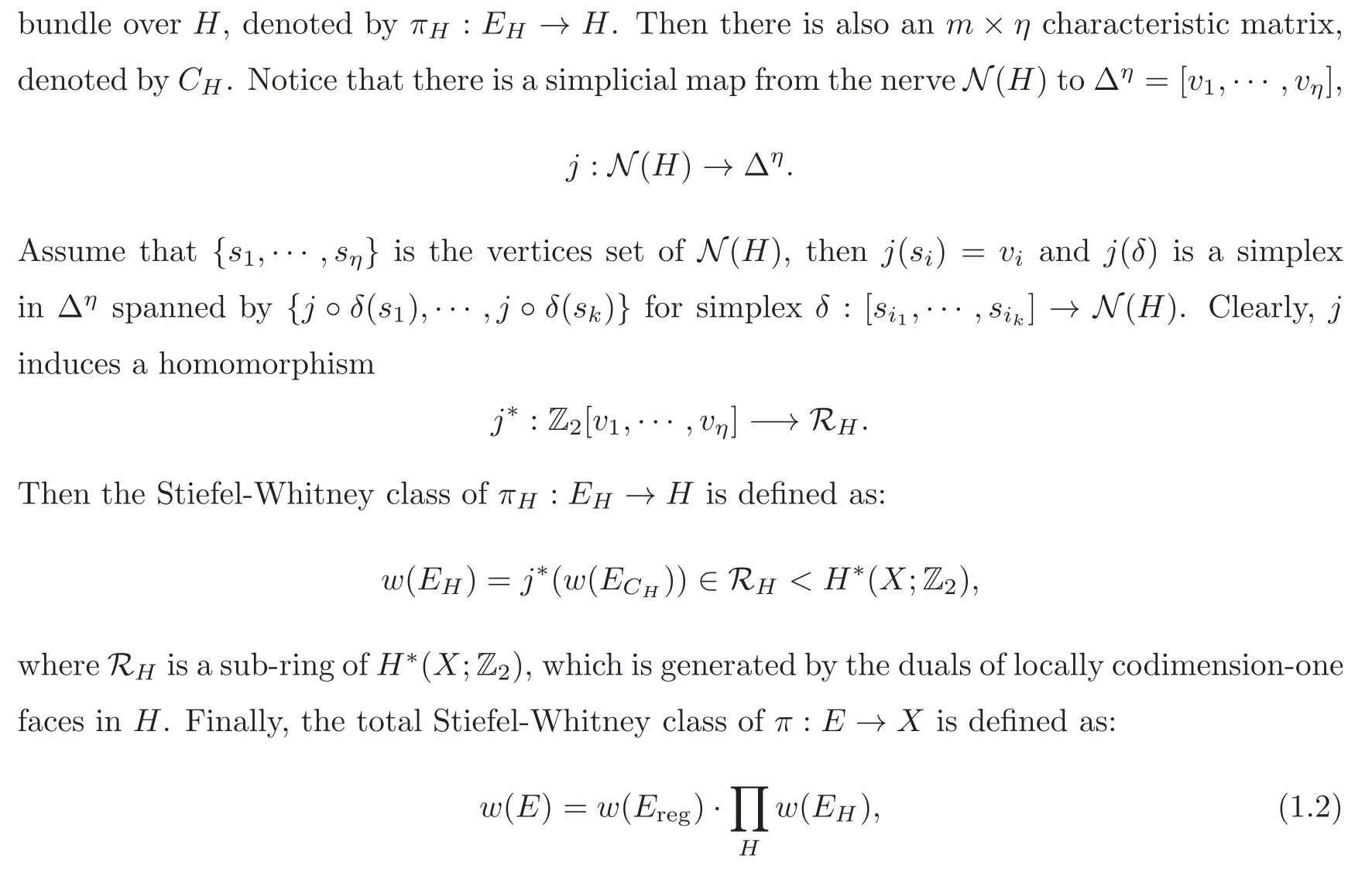
This paper is organized as follows.In Section 2,we give some preliminaries.In Section 3,we define Stiefel-Whitney classes of real orbifold vector bundles overIn Section 4,we consider the general cases,that is,Stiefel-Whitney classes of real orbifold vector bundles over a right-angled Coxeter complex.In Section 5,we prove Theorem 1.1 and give some examples.

2 Preliminaries

2.1 Right-Angled Coxeter orbifolds and right-angled Coxeter complexes

2.2 Cohomology rings of right-angled Coxeter complexes

For a right-angled Coxeter complex,one can define a cellular chain complex,by the result in[12].

2.3 Orbifold vector bundle

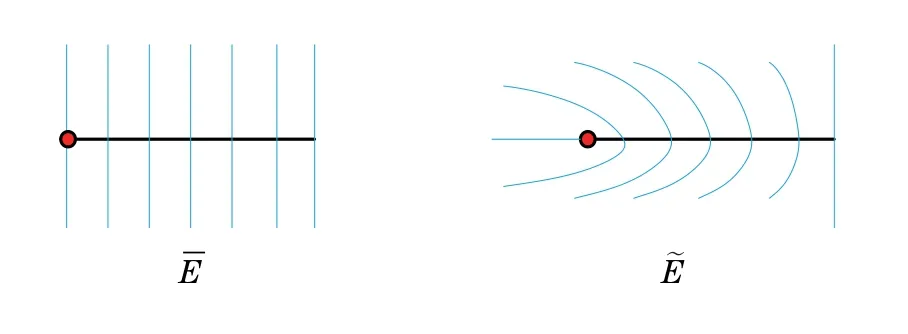
Figure 1 Orbifold line bundles over D1/2.

2.4 The linear representation of(2)k

All group actions in the next are supposed to be locally linear actions.The reflection across a coordinate hyperplane inis called a standard reflection.

3 Orbifold Stiefel-Whitney Classes of Real Orbifold Vector Bundles over Dn/(2)k

4 The Real Orbifold Vector Bundle and Orbifold Stiefel-Whitney Classes over Right-Angled Coxeter Complexes

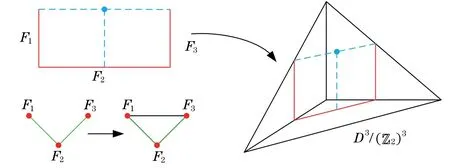
Figure 2 Embedding of right-angled orbifold complexes.

5 Application and Examples

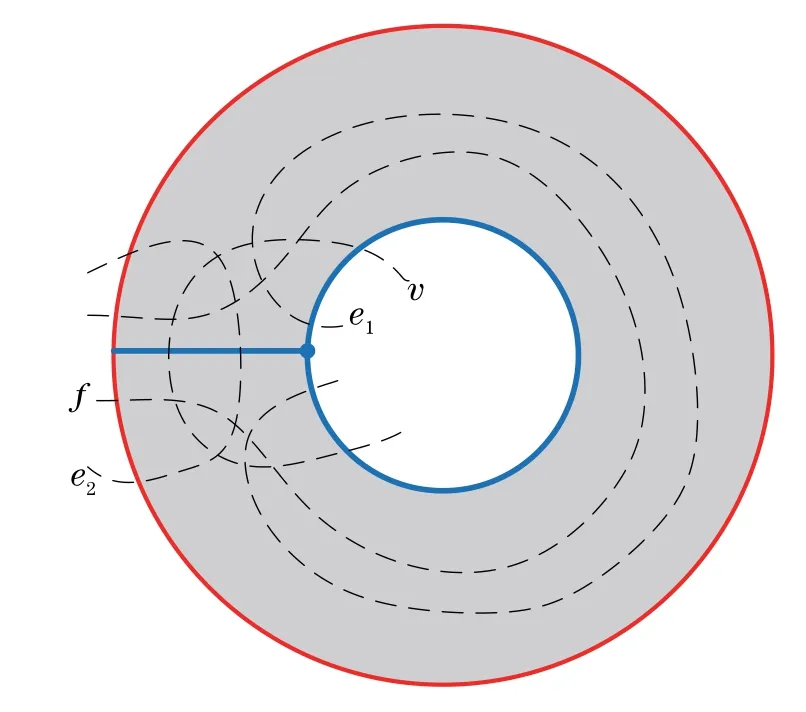
Figure 3 S1×[−1,1]/Z2.

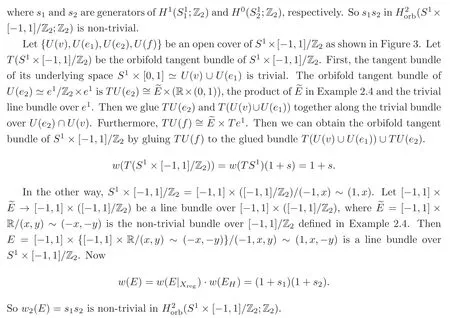
AcknowledgementI would like to thank my mentor Professor Zhi L¨u for useful suggestions and valuable discussions,and thank the anonymous referees for valuable suggestions and comments which have improved this paper.