Exact Boundary Controllability of Weak Solutions for a Kind of First Order Hyperbolic System—the HUM Method∗

Xing LU Tatsien LI

1School of Mathematics,Southeast University,Nanjing 211189,China.E-mail:xinglu@seu.edu.cn

2School of Mathematical Sciences,Fudan University,Shanghai 200433,China;Shanghai Key Laboratory for Contemporary Applied Mathematics;Nonlinear Mathematical Modeling and Methods Laboratory.E-mail:dqli@fudan.edu.cn

Abstract The exact boundary controllability and the exact boundary observability for the 1-D first order linear hyperbolic system were studied by the constructive method in the framework of weak solutions in the work[Lu,X.and Li,T.T.,Exact boundary controllability of weak solutions for a kind of first order hyperbolic system —the constructive method, Chin.Ann.Math.Ser.B,42(5),2021,643–676].In this paper,in order to study these problems from the viewpoint of duality,the authors establish a complete theory on the HUM method and give its applications to first order hyperbolic systems.Thus,a deeper relationship between the controllability and the observability can be revealed.Moreover,at the end of the paper,a comparison will be made between these two methods.

Keywords First order linear hyperbolic system,Exact boundary controllability,The HUM method

1 Introduction

First order linear hyperbolic systems are widely used to model various systems in real life,such as traffic flow,fluids in open channels and light propagation in optical fibers,etc.The exact boundary controllability and the exact boundary observability for 1-D first order hyperbolic systems(even in the quasi-linear case)have been established by the constructive method in the framework of classical solutions(see[4–6]).In[12],we established the exact boundary controllability and the exact boundary observability for 1-D first order linear hyperbolic systems in the framework of weak solutions by the constructive method.In this paper,we are going to study these problems from the viewpoint of duality,namely,by the corresponding HUM method.

The HUM method was proposed by J.-L.Lions for a single wave equation with Dirichlet boundary control or Neumann boundary control(see[10–11]).He used an observability inequality to establish the controllability by the HUM method.Later,for a coupled system of wave equations,the exact boundary controllability was set up under Dirichlet boundary controls(see[8])and Neumann boundary controls(see[9])in suitable Hilbert spaces by the HUM method,respectively.The HUM method applying to a system of transport equation can be found in[2].

In the linear case,by studying the controllability through the HUM method in the framework of weak solutions,a deeper relationship between the controllability for the original system and the observability for the corresponding adjoint system can be revealed.

For the 1-D first order hyperbolic system,although in the framework ofC1solutions,the controllability and the observability have been completely established,however,theC1space is not a Hilbert space,in which the HUM method can not be adopted to get the controllability by duality even in the linear case.Since the first order hyperbolic system is time irreversible in general,differently from the time reversible system like the wave equation,the corresponding HUM method will have its own difficulty,which was called as the RHUM method by J.–L.Lions in[10].However,for simplicity,we will still call it as the HUM method in this paper.Here we mention that the authors of[1]considered the boundary controllability from the perspective of duality,but the observability inequality based on energy estimates applied in that paper are valid only for certain class of symmetric hyperbolic systems,which can not be extended to general cases,moreover,the HUM method for the first order hyperbolic system was not explained there.

Thus,to our knowledge,there is still no paper that explains thoroughly the HUM method and its applications for first order hyperbolic systems,then we intend to establish a complete theory on the HUM method for first order linear hyperbolic systems to obtain the controllability,and further apply it to study the problem of synchronization in a forthcoming paper.

The system under consideration is given by

Then,based on a strong observability inequality,we can construct an isomorphism between the final dataUTof system(1.1)–(1.3)and the final data ΦTof the adjoint system(1.5).Thus,for any givenUT(x)∈(L2(0,L))n,there exists ΦT(x)∈(L2(0,L))nsuch that the corresponding adjoint problem(1.5)–(1.6)admits a weak solution Φ =Φ(t,x).This procedure can uniquely determine the boundary control function so that the solution to problem(1.1)–(1.4)satisfies exactly the final state(2.6)below at the timet=T.Hence,if the strong observability inequality holds for adjoint system(1.5),then system(1.1)–(1.3)is exactly controllable.

By duality,we can see more clearly the close relationship between the exact boundary controllability for system(1.1)–(1.3)and the strong exact boundary observability for adjoint system(1.5).Moreover,the boundary control provided by the HUM method should possess the leastL2norm among all the boundary controls realizing the exact boundary controllability,which will be proved in Subsection 2.3 in the case of two-sided controls.

By Theorem 3.3 and Remark 3.3 in[12],we have

We will establish the exact boundary controllability for system(1.1)–(1.3)by the HUM method based on the duality in this paper.The case of two-sided controls and the case of one-sided controls will be successively discussed in Section 2 and Section 3,respectively.Then the constructive method and the HUM method will be compared in Section 4.

2 Two-Sided Exact Boundary Controllability of Weak Solutions by the HUM Method

2.1 Two-sided exact boundary controllability

We first prove the two-sided exact boundary controllability for system(1.1)–(1.3)based on the following lemma of strong observability.

2.2 Relationship between the controllability for the system and the strong observability for the adjoint system

2.3 Optimality

3 One-Sided Exact Boundary Controllability of Weak Solutions by the HUM Method

4 The Comparison Between the Constructive Method and the HUM Method

Both the constructive method and the HUM method can be used to establish the exact boundary controllability for system(1.1)–(1.3)(see Lemmas 4.1–4.2 in[12]and Theorem 2.1,Theorem 3.1 in this paper).They obtain almost the same results from two different points of view:The constructive method is to construct a solution,satisfying exactly the given initial data and final data,by successively solving some forward problem,backward problem,leftward(resp.rightward)problem of system(1.1)–(1.3)with suitable artificial boundary conditions.It is more direct and easier to be understood.While,the HUM method treats the problem by means of the duality,the problem of controllability is then transformed into a problem of observability for the homogeneous adjoint system.Then,to prove the observability inequality is to make estimates of the solution to this homogeneous system.We will make some comments about these two methods in what follows.

1.The constructive method can be easily used to establish not only the controllability of a system,but also the observability of the adjoint system.While,for the HUM method,to prove the controllability of a system is based on the observability inequality of the adjoint system,and in this paper,the observability inequality is also proved by the constructive method.

2.For the problem with inhomogeneous boundary conditions,the constructive method can be also used to establish its controllability and observability.For example,for one-sided exact boundary controllability,by Lemma 4.2 in[12],system(1.1)–(1.3)is exactly controllable for any given boundary control matrixD0and boundary functionH+(t)under some hypotheses.But in order to apply the HUM method,we have to assume that there is no boundary control onx=0,namely,H+(t)≡0 in(1.2).Otherwise,(3.11)becomes

and(3.12)becomes

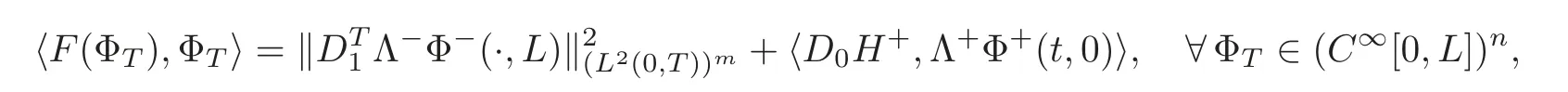
then 〈F(ΦT),ΦT〉 can not define a semi-norm,hence the HUM method fails.

3.The constructive method can be efficiently applied to deal with problems in one-dimensional space,but very difficult for higher dimensional spaces.However,to consider the problem by means of the duality in the framework of weak solutions will be possible and helpful for the study in higher dimensional spaces.

4.By the HUM method,the close relationship between controllability and observability can be better revealed.Take a coupled system of wave equations as an example,two important and difficult issues can be solved by the duality in the study of synchronization and related problems,one is the non-controllability when there is a lack of boundary controls,while,the other is the necessity of the compatibility conditions of the coupling matrix for synchronization.As to the first issue for first order hyperbolic systems,so far there is no further result except for some special decoupled equations(see[7]).As to the second issue,we will take into consideration together with related subjects of synchronization for first order hyperbolic systems in our future work.

5.In the proof of controllability by the constructive method,although the boundary control can be obtained,however,taking the case of one-sided controls for instance,we have to solve a forward problem,a backward problem,then a rightward(resp.leftward)problem.While,by the HUM method,since the boundary control is determined by the solution to the adjoint problem,we only have to solve a backward problem,and the obtained boundary control has an explicit expression.Moreover,the boundary control provided by the HUM method possesses the leastL2norm.

6.The HUM method is not available in dealing with the exact boundary null controllability for first order hyperbolic systems in general.In fact,when the corresponding weak exact boundary observability inequality holds,since the first order hyperbolic system may not be time reversible,we do not have similar inequalities as(1.8)–(1.9)with respect to the initial data,then we can not obtain an isomorphic mapping asF,so that the HUM method does not work.

7.In the framework of weak solutions,system(1.1)–(1.3)is still exactly(null)controllable when the control timeTis equal toT0.However,in the framework of classical solutions,in order to guarantee the continuity of the constructed solution,it sharply requiresT >T0,which is determined by the regularity requirement of the classical solution,but not required in the framework of weak solutions.This property is still true for related results on the observability.