Unique Continuation on Quadratic Curves for Harmonic Functions∗

Yufei KE Yu CHEN

1School of Mathematics,Shanghai University of Finance and Economics,Shanghai 200433,China.E-mail:keyufei@163.sufe.edu.cn

2Corresponding author.School of Mathematics,Shanghai University of Finance and Economics,Shanghai 200433,China.E-mail:yuchen@sufe.edu.cn

Abstract The unique continuation on quadratic curves for harmonic functions is discussed in this paper.By using complex extension method,the conditional stability of unique continuation along quadratic curves for harmonic functions is illustrated.The numerical algorithm is provided based on collocation method and Tikhonov regularization.The stability estimates on parabolic and hyperbolic curves for harmonic functions are demonstrated by numerical examples respectively.

Keywords Unique continuation,Quadratic curves,Harmonic function

1 Introduction

In this paper,we consider a problem that how to get global information by using local given information of the solution,namely,a unique continuation problem.The unique continuation for an elliptic equation states that if there is a connected open set Ω ∈Rnin which the solutionulies and Ξ ⊂Ω is an open subset of Ω,thenu|Ω≡0 providedu|Ξ=0.In two dimensions,the unique continuation means that an analytic function must be zero if its zero points have accumulated points.We will first consider a parabolic curve,which is an analytic submanifold of two dimensional space.The aim is to study unique continuation on a parabola for harmonic functions,that is,if the value of functionuis known on a small part of the parabolic curve,then how to get the value ofuon a larger piece of the parabola.This problem is non-trivial since no measurement on the boundary∂Ω is given.Moreover,it is an ill-posed problem due to its instability,which causes difficulties in numerical computations.For other types of quadratic functions,similar results can be obtained by the methods in this paper.

In the understanding of the unique continuation,unique continuation properties of various PDE’s have been proved with development of PDEs theory(see[1]).Recently,the unique continuation on analytic sub-manifold has also been studied.For instance,Cheng and Yamamoto[2]fixed the measure points on a line and proved the conditional stability on a line for twodimensional harmonic functions by adopting the method of complex continuation.Based on their results,Lu et al.[3]derived the unique continuation on a line for Helmholtz equation and the numerical treatment was firstly considered in their paper.The conditional stability of line unique continuation can also be applied to the estimation of unknown boundary for harmonic functions(see[4]).Besides,the unique continuation has also been applied to the studies of other inverse problems,like control theory and optimal design problems.For example,the stability of soft obstacles reconstruction in inverse scattering was obtained by Isakov[5]based on unique continuation.Cheng et al.[6]studied the unique continuation for elasticity systems,which can be applied in phase transformation and anomalous diffusion in heterogeneous medium.

The focus of this paper is to generalize the conclusions of Cheng and Yamamoto[2]on a line to quadratic curves.A conditional stability for the continuation problem will be obtained based on the complex extension method,the unique continuation property is then implied.The main idea is to construct a holomorphic function based on the integral of single-layer potential with Green’s function.The determination of the analytic domain of the complex extention is a key to this process,which differs from the case of unique continuation on a line.After obtaining conditional stability estimates,a deterministic regularization,Tikhonov regularization,can be used to deal with the ill-posedness and construct stable numerical method(see[7]).Considering the discontinuity of real measurements,refer to[8],the collocation method can be used to make specific numerical applications.

Our problem can be formulated as follows.Assume that Ω is a domain in R2,Γ is an analytic curve and a continuous parabola in Ω.Suppose that there exist open curvesτandTsatisfying:τ⊂T⊂⊂Γ.Consider a harmonic functionu(x)in Ω,such that:

Then this paper principally discusses the unique continuation on curveTforuwhich is known onτ(as illustrated in Figure 1),including the conditional stability estimate and the numerical computation.It should be pointed out that Cauchy values are not needed by our results,that is,no derivatives of harmonic functions on quadratic curves are required.

Figure 1 Illustration of unique continuation on a quatratic curve T with the measurement segment τ for a harmonic function u in Ω.

Figure 2 Unique continuation on parabolic equation for harmonic function:The capital of each subfigure means the collocation points on τ.

Figure 3 Harmonic measure:The capital of each subfigure means the collocation points on τ.

The rest of this paper is organized as follows:Section 2 gives the proof of the conditional stability on quadratic curves for harmonic functions,requiring that the taken curve segments have no intersections with boundaries.In Section 3,numerical applications implemented by the collocation method and Tikhonov’s regularization are given.The numerical calculations on parabolic and logarithmic equations for harmonic functions,respectively,illustrate the validity of the conditional stability estimates.Conclusions are drawn in Section 4.

2 The Unique Continuation for Harmonic Functions

3 Numerical Methods and Applications

3.1 Parabolic curve

Remark that the harmonic measureϕdecides the degree of control for u on T,from Figure 3,if we define that the points withare good-controlled points,then we can see that the good-controlled points only appear when nearing to the controlled points.Consider the situation of two fixed sections,the line ofϕbetween two fixed lines can be controlled better.However,if two sections are far away enough,the line in the middle between them still cannot be controlled well.

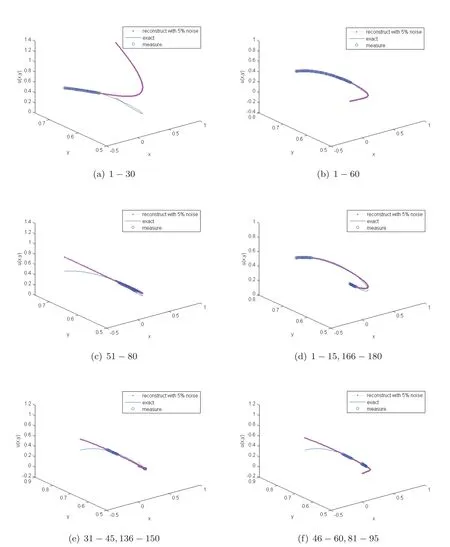
Figure 4 Unique continuation on hyperbolic equation for harmonic function:The capital of each subfigure means the collocation points on τ.

From Table 2,it can be seen that when the controlled points are same,it is obvious that the smaller observation error,the more accurate the estimation result.When the observation error is controlled at the same level,the accuracy of the estimated results from Case a to Case d is significantly improved.In Case d,when the first 30 points and the last 30 points of the 180 points are controlled,as can be seen from the table,even if there is an error of 5% in the observed valueu|τ,the estimated resultu|Tis still very close to the accurate valuef,the error is only of order 10−1.

Table 1 List of numerical cases.

Table 2 Error on the parabolic curve.

Table 3 Error on the hyperbolic curve.

3.2 Hyperbolic curve

Table 3 shows the similar conclusion as the conclusion from Table 2,which illustrates that the conditional stability estimate in(2.2)is valid.

The specific results of multiple sections will be discussed in subsequent papers.

4 Conclusion

This paper obtains the unique continuation on quadratic curves for harmonic functions.Similar to the results on a straight line for harmonic functions,the unique continuation and the conditional stability are proved.A difference is that the complex extension on the quadratic curves is more complicated.Due to the complexity of the complex extension of the function on the quadratic curve,it is necessary to consider the selection of the complex extension region and the harmonic measure.

In this paper,the unique continuation of two types of curves(parabola and hyperbola)are calculated numerically by means of collocation method and Tikhonov regularization.The calculation takes into account the length,position and number of segments of the controlled curves.Through comparison,it is found that the lengths of control rangeτhave no significant results on estimation ofu|T,but the multi-stage control can achieve more accurate results.These numerical applications are consistent with the theoretical results in this article and[2].Thus in applications,when data on a quadratic curve need to be measured,according to the description of this paper,only a part of data,instead of all the data need to be measured directly,which reduces the measurement cost significantly.