分区达标法贡献度系数计算与研究
2022-03-14陈莉苹张舟
陈莉苹 张舟
(1. 中节能国祯环保科技股份有限公司,安徽合肥 230088;2. 珠江水资源保护科学研究所,广东广州 510611)
1 引言
科学合理地计算水环境容量及总量分配是流域水环境达标的前提[1-3],早期水环境容量的计算依靠传统的试算法,即根据经验调整污染负荷分布进行反复试算,直到水域环境功能区达标为止,该方法适用于简单排污情况,但在排污口众多的时候,采用试算法工作量巨大且不是最优解[4]。为解决此问题,李适宇等[5]于1999 年提出分区达标法,该方法通过引进贡献度系数的概念将二维容量问题转化为线性规划问题,避免了在海域排污口众多时,传统试算法带来的巨大工作量,通过将水质模型与线性规划模型耦合,可以合理而精确地求取海域水环境容量。
2010 年郑洪波等[6]将此方法应用在大连金港区,给出了不同污染物(如COD、无机氮等)的海洋环境容量,建立了计算海洋环境容量的普遍方法;2015 年王宇骏等[7]综合考虑效益、公平与水质要求,改进了分区达标法,并将改进的模型应用于流溪河水环境容量的计算。2018 年王程等[8]选取多种因素如人口、GDP、水资源量、工业产值、工业废水排放量、环保投资等建立优化分配模型,提出削减方案,指导兰江流域水质管理。
以上主要采用分区达标法来求解水环境容量,对于贡献度系数的定义偏向于理论假设,未能同实际相结合。本文拟通过分区达标法中对贡献度系数的理论描述,运用MIKE11 水环境模型计算出各污染源贡献度系数,再采用MATLAB 拟合,得出贡献度系数与污染源浓度、流量以及污染源与考核断面距离之间的定量化关系,据此提出单位负荷贡献度系数的概念及其表达式,并将其应用于新安涌黑臭治理中,量化河涌现状污染状况。
该研究可为后续总量分配提供计算依据,便于更准确贴合实际的总量分配,为后续水环境信息化管理作量化依据。
2 贡献度系数研究
贡献度系数是分区达标法中的关键概念,在分区达标法中通过引入贡献度系数,可以将容量问题转化为线性规划问题,从而求取最优的环境容量。
贡献度系数定义可以表示为[5]:假设一条河流共有n 个排污口,m 个考核断面,在1 个排污口给定1 个单位负荷量,即xj=1,其他排污口无负荷量排出,即xk=0(k=1,…,n;k≠j),通过模型计算出这种情况下的浓度分布,确定出m 个水质控制断面的浓度值,即为此排污口对考核断面的贡献度系数aij(i=1,…,m),改变排污口,重复以上步骤,就可以求出每个排污口的aij。在以上所有计算中,开边界上的浓度为0,即不考虑背景浓度。
根据贡献度系数定性定义,可以看出影响贡献度系数的主要因子为排污口负荷量以及排污口与水质控制断面的距离,具体来说主要影响因子有排污口流量(Q)、浓度(C)以及排污口与水质控制断面距离(L)。
以下以实际河涌为研究对象,通过MATLAB 拟合出贡献度系数与其主要影响因子之间的定量化关系。
2.1 研究概况
选取中山市新安涌作为研究对象,河涌长度为1.1 km,其水文条件受感潮影响不大。根据污染源调查,该河涌旱季有水排口共15 个,其中,分流制污水排口2 个,分流制雨污混接雨水排口10 个;旱季无水排口28 个。本次研究旨在定量化贡献度系数与流量、浓度以及距离之间的关系,因此选用分流制雨污混接雨水排口,排口分布及编号如图1 所示。
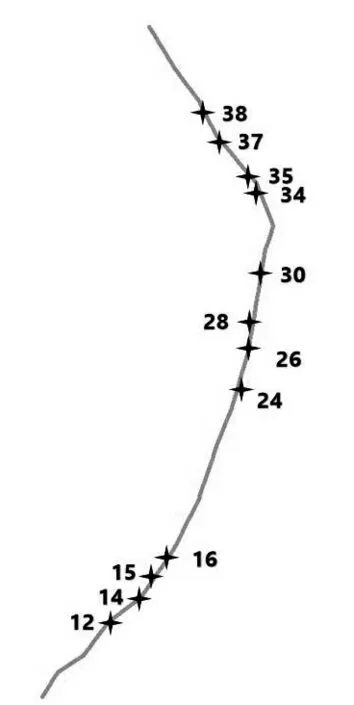
图1 新安涌有水排口分布示意
2.2 研究方法及原理
原理主要包括两部分,MIKE11 模型计算原理和MATLAB 拟合方法。
2.2.1 MIKE11 模型计算原理
MIKE11 水动力学模型主要基于HD 模块,以圣维南(Saint-Venant)方程组为控制方程,利用Abbott六点隐式格式离散圣维南控制方程组,之后再用河道方程、汊点方程组、外边界条件等解出隐式方程组,得到水动力参数。MIKE11 水质模型以一维对流扩散方程作为控制方程,方程可以表示为:
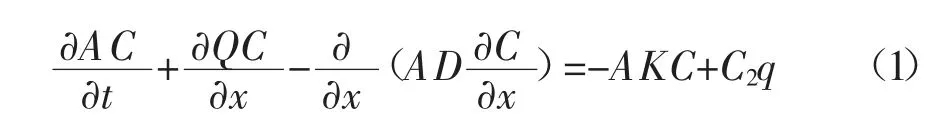
式(1)中,C 为污染物浓度,mg/L;D 为扩散系数,m2/s;A 为横截断面面积,m2;K 为衰减系数,s-1;C2为源汇浓度,mg/L;q 为旁侧入流,m3/s;x 为空间坐标,m;t为时间坐标,s。
采用时间和空间中心隐式差分格式对上述控制方程进行离散,再利用水质边界条件、各种水质过程的模拟及水质过程与对流扩散耦合计算来求解离散方程。
2.2.2 MATLAB 拟合方法
根据数据特点,本研究选取多项式拟合或者自定义方法,求出变量之间的定量化关系。
2.2.2.1 多项式拟合
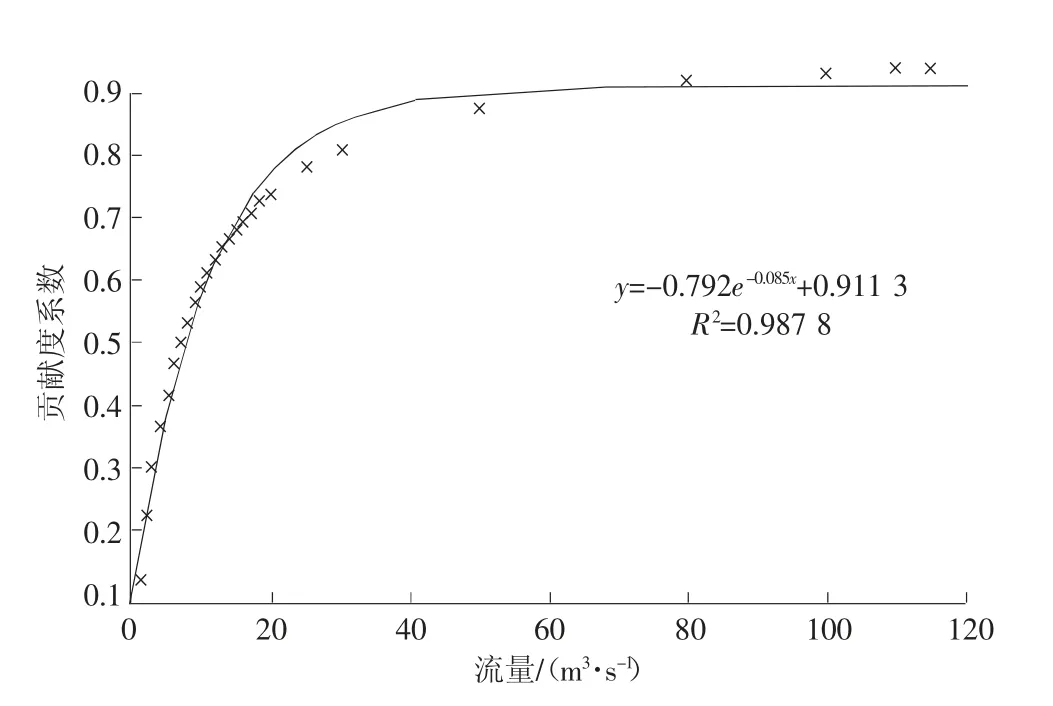
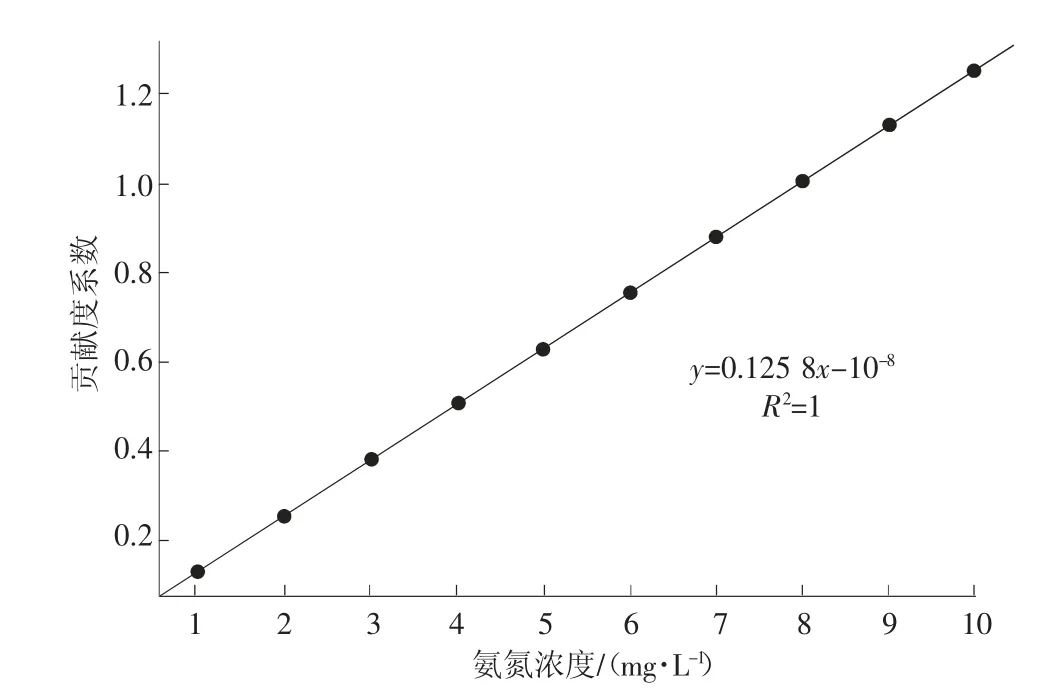
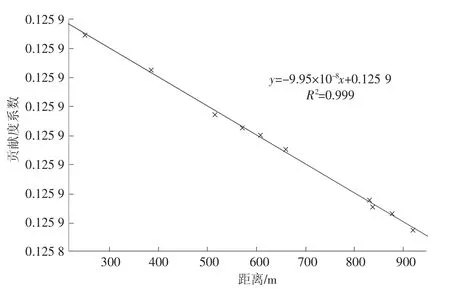
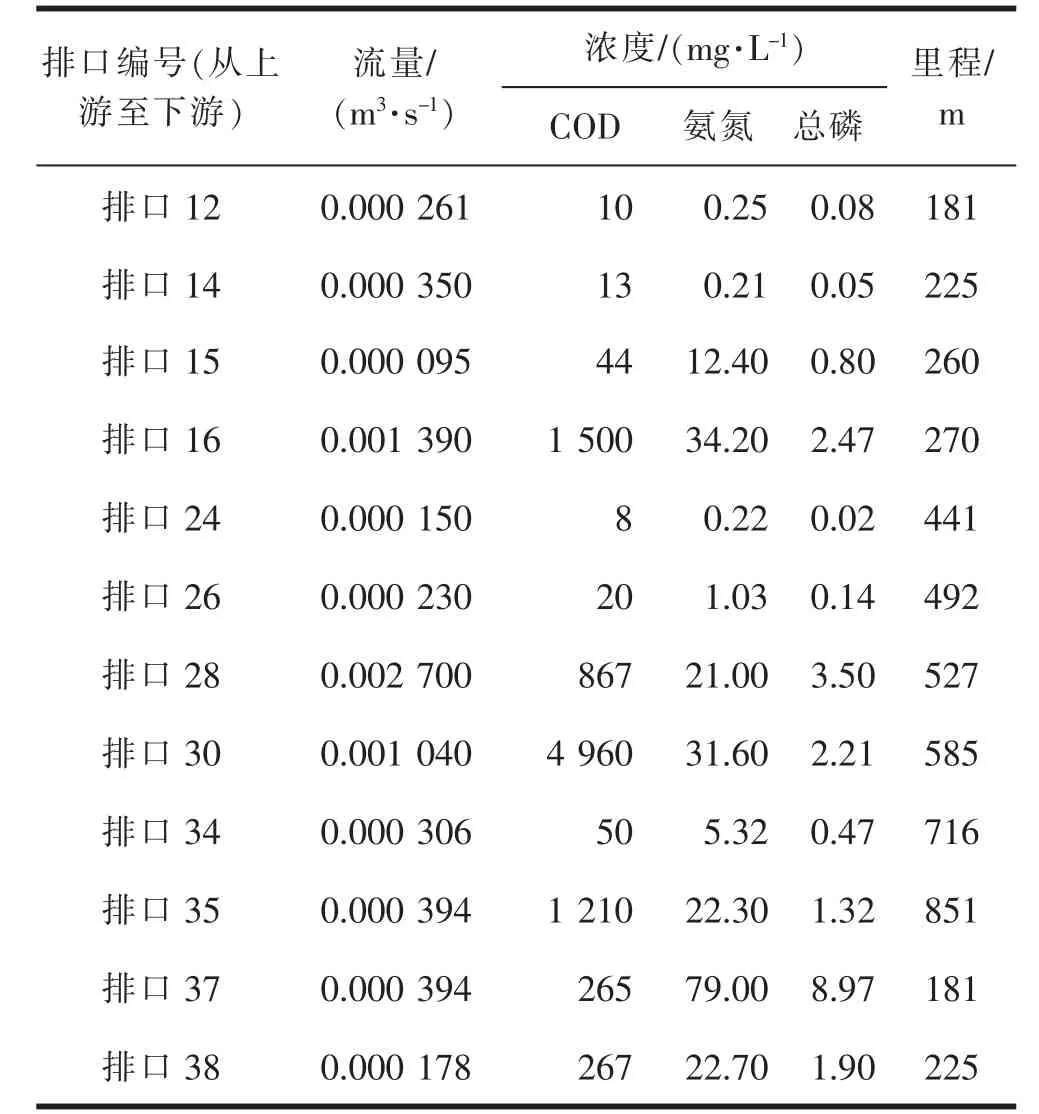
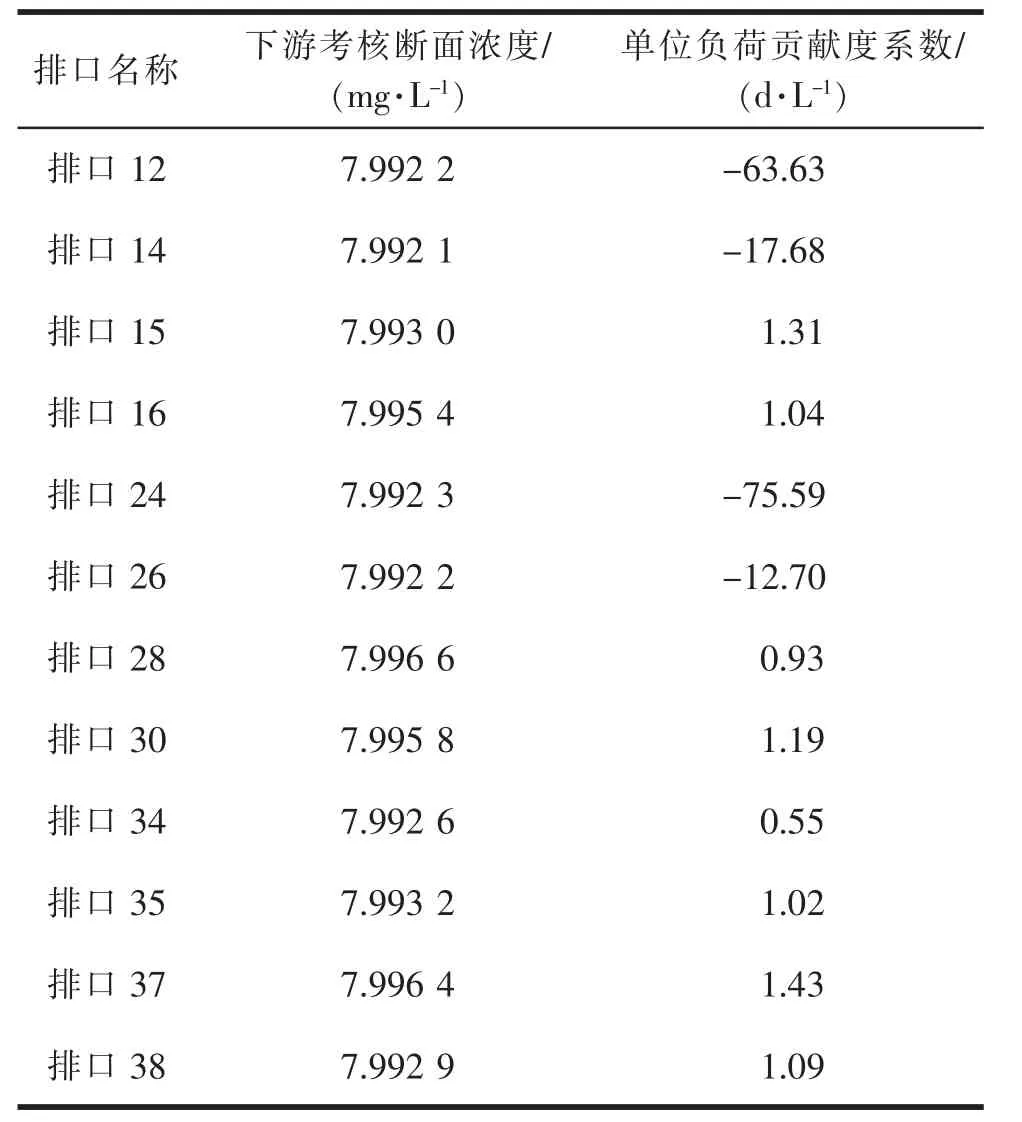
将原始数据散点用多项式函数进行拟合,即为多项式拟合。设由数据得到的函数y=f(x)在n 个点x1,x2,…,xn的值为y1,y2,…,yn,采用多项式Øm(x)来拟合,设Øm(x)=a0+a1x1+a2x2+…+amxm(m 对式(2)求解,使得Q(a0,a1,…,am)达到最小,由此确定多项式系数。 在MATLAB 中多项式拟合的实现方式为polyfit函数或者polyval 函数,可以对其直接调用。 2.2.2.2 自定义法 若数据特点不符合多项式规律,则需要采用自定义方法确定,根据数据特点,函数可能为指数函数,其一般表达式为f(x)=a×exp(-b×x)+c,通过调用MATLAB 中的fit 函数可以进行指定函数的数据拟合,确定系数a,b,c,从而得出函数关系式。 2.3.1 贡献度系数与流量的关系 设定浓度和距离不变,选取氨氮为指标,研究贡献度系数与流量的关系。具体来说,选定新安涌排口12,给定1 个单位浓度(1 mg/L),增大排口流量,分析流量对水质及贡献度系数的影响。分两种情况讨论。 2.3.1.1 排口氨氮浓度大于背景浓度 当排口氨氮浓度大于河涌背景浓度时,排口会加重河涌污染。以排口12 为例,河涌背景的氨氮浓度设置为0 mg/L,计算出下游考核断面浓度及贡献度系数,以贡献度系数为因变量y,流量为自变量x,MATLAB 拟合结果如图2 所示。从图2 可以看出,随着流量增加,贡献度系数逐步增大,增加至数值0.9 附近后趋于平缓。贡献度系数与流量关系式为:y=-0.792e-0.085x+0.911 3,相关性系数R2=0.987 8,可以看出,当排口氨氮浓度大于河涌背景浓度时,排口流量与贡献度系数呈指数关系,流量增加,贡献度系数增大。经过试验研究,流量增加极限为115 m3/s,往后会影响模型的稳定性。 图2 流量与贡献度系数关系(C 排口>C 背景) 2.3.1.2 排口氨氮浓度小于背景浓度 当排口氨氮浓度小于河涌背景浓度时,排口的排放会增加河涌稀释流量。本次河涌背景的氨氮浓度设定为上游实际来水浓度(1.5 mg/L),排口12 的氨氮排放浓度给定为1 mg/L,流量值依次增大,流量与贡献度系数关系见图3。从图3 可以看出,当排口氨氮浓度大于河涌背景浓度时,随着流量的增加,贡献度系数逐步减小,其减小幅度随流量持续增加而趋于平缓,最终其数值接近-0.47。以贡献度系数为因变量y,流量为自变量x,通过MATLAB 拟合得出贡献度系数与流量关系式为:y=3.399 5e-0.084x-0.457 6,相关性系数R2=0.989 5,排口流量与贡献度系数呈负相关关系,流量增加,贡献度系数减小。 图3 流量与贡献度系数关系(C 排口 2.3.2 贡献度系数与浓度的关系 设定流量和距离不变,选取氨氮为指标,研究贡献度系数与浓度的关系。具体来说,选定排口12,给定1 m3/s 的流量,氨氮浓度值依次从1 mg/L 增大到10 mg/L,计算出下游考核断面浓度及贡献度系数,拟合结果如图4 所示。从图4 可知,排口氨氮浓度与下游考核断面浓度呈标准线性关系,拟合函数关系式y=0.125 8x-10-8,排口氨氮浓度越大,贡献度系数越大。 图4 排口氨氮浓度与贡献度系数的关系 2.3.3 贡献度系数与距离的关系 设定排口流量、浓度不变,取河涌12 个排口进行计算,其里程由小到大。 选取氨氮为指标,模型背景氨氮浓度全部设置为0 mg/L,12 个排口的浓度和流量都给定1 个单位(1 mg/L),各排口贡献度系数如图5 所示。由图5 可见,排口与考核断面距离越大,贡献度系数越小,拟合的函数关系式y=-9.95×10-8x+0.125 9,表明距离和贡献度系数呈负相关,线性斜率k=-9.95×10-8,其值非常小,因此距离对贡献度系数影响很小,计算时不做定量考虑。 图5 距离和贡献度系数的关系 根据上述拟合结果,贡献度系数与距离和浓度均呈线性关系,与流量呈指数关系,其中影响贡献度系数的主要因素为浓度和流量。 分区达标法中贡献度系数计算的设定不考虑背景浓度,偏向比较理想状态,而在实际计算应用中,需要加入背景浓度以更贴合实际情况,由此引入单位负荷贡献度系数(aij),其表达式可表示为: 式(3)中,i 为考核断面个数,共m 个;j 为排口个数,共n 个;Cij为第j 个排口单独排放时目标考核断面浓度,mg/L;Cbj为目标考核断面背景浓度,mg/L;Cj为第j 个排口的排放浓度,mg/L;Qj为第j 个排口的排放流量,m3/s。 式(3)中,Cij主要通过MIKE11 水质模型计算得出,aij的单位为d·L-1,从单位上看,单位负荷贡献度系数主要与流量有关。 选择新安涌作为实际案例应用,采用MIKE11模型计算各排口单独排放时下游考核断面浓度,再根据式(3)计算各排口单位负荷贡献度系数。 根据污染源调查及实测资料,新安涌排口的基本情况(浓度、流量、与上游距离)如图1 和表1 所示。从表1 可以看出,排口水质部分相差很大(排口16,30,35),大多属于分流制混接排口,有学校、政府等生活污水汇入。 表1 新安涌有水排口概况 根据污染源调查,新安涌主要污染物为氨氮,因此计算以氨氮为指标,采用MIKE11 准确计算新安涌排口单独排放时下游考核断面浓度。 模型设置:上游设置流量边界,新安涌上游来水为新安村大小水坑和城桂路排洪渠,流量为7.27 m3/s;下游设置水位边界,新安涌下游与白石涌相连,以河道下游常水位作为河道水动力的下游边界值,新安涌下游常水位取1.5 m。 新安涌治理目标为消除黑臭,上游来水为黑臭水质,则氨氮初始值为8 mg/L,氨氮的降解系数取0.12 d-1。 各排口下游考核断面浓度根据公式(3)计算的单位负荷贡献度系数见表2。单位负荷贡献度系数为负值的共有4 个排口,分别为排口12,14,24,26,这4 个排口对新安涌水质变好有促进作用;其他排口单位负荷贡献度系数均为正值,这些排口会加重新安涌水质污染。贡献度系数值越大,对新安涌水质污染越大,表2 中排口37 水质污染最大。 表2 考核断面浓度和单位负荷贡献度系数 在河涌黑臭治理中,需要着重治理贡献度系数大的排口,贡献度系数为负值的排口,对河涌的水质有一定的正向作用,后续可通过量化分配,将水环境容量分配至每个排口,实现优化分配。 (1)对分区达标中的贡献度系数进行了详细研究,分析了贡献度系数及其影响因子,MATLAB 拟合结果表明,贡献度系数与污染源浓度、污染源与考核断面距离之间呈线性关系,与流量呈指数关系,贡献度系数主要影响因子为浓度和流量。 (2)根据贡献度系数定义以及影响因子研究结果,提出了单位负荷贡献度系数的概念并给出其计算表达式,该公式考虑了背景浓度,可以更贴合实际情况。 (3)通过新安涌实际案例计算,验证了单位负荷贡献度系数表达式的实用性,通过计算单位负荷贡献度系数可以对河涌排口治理有初步判断,后续拓展至流域可以量化流域水质现状,对于流域水环境治理有实际的指导意义。 (4)贡献度系数的研究可以为后续总量分配提供计算依据,便于将分区达标法求取的最优水环境容量分配至每个排口或污染源。该研究考虑了河涌背景浓度,有利于与运营实际相结合,可以更准确贴合实际的总量分配,便于后续流域水环境信息化管理。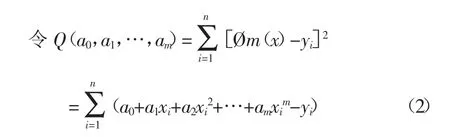
2.3 研究结果

2.4 单位负荷贡献度系数
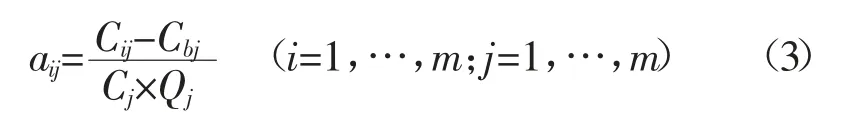
3 实际案例应用
3.1 新安涌排口基本资料
3.2 MIKE11 水环境模型
3.3 单位负荷贡献度系数计算
4 结论及展望
