对2021年高考浙江解析几何题的探究及命题技术探讨

湖北省恩施州教育科学研究院(445000)周威

湖南省长沙市雷锋学校(410217)童继稀

一、试题呈现与问题的提出

评注本题考查了有关抛物线的基础知识与通性通法(即用联立方程解决直线与曲线的位置关系),同时将转化与化归、函数与方程等基本思想融入其中,最后落脚于“范围”问题,凸显了高考评价体系“四翼”中的基础性、综合性.解决本题的关键是将等式关系|RN|2=|PN|·|QN|进行坐标转化,再通过联立直线与抛物线方程、直线与直线方程得到相关各点的坐标关系,代入等式关系可得相关参数的关系式,最后从函数的角度回归到“范围”问题.该题入口低、层次分明、落差大,对学生的数学抽象、数学运算与逻辑推理等核心素养的要求相对较高,同时也体现出了命题者高超的命题技术与水平.

根据以上分析,以及按部就班的数学运算与站在命题的角度反思,有以下几个问题值得深入探讨.

问题1此题抛物线情境中,命题者考虑到了哪些性质?

问题2为什么命题者选择等式关系|RN|2=|PN|·|QN|作为条件,若抛开抛物线的情境背景,命题者又关联了平面几何中哪些与三角形有关的性质?

问题3历年高考和平常教学中有哪些类似的命题经验和案例?

本文围绕这3 个问题进行研究和探讨.

二、情境中的圆锥曲线性质探究

三、去情境化的平面几何性质探究

四、命题技术的总结及类似案例

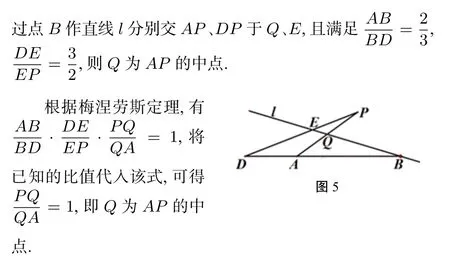
法国数学家拉普拉斯说,在数学里发现真理的工具主要是归纳和类比.而将归纳和类比运用到高考真题的命题立意探究中来,是数学教师的一种专业素养,有利于教师的解题教学与命题能力提升.它也是复习备考中真正跳出“题海战术”的表现,同时也是高考评价体系“一核四层四翼”中“一核”引导教学的表现.