由一道椭圆题谈利用伸缩变换简解解析几何题

安徽省芜湖市第一中学(241000)刘海涛

安徽省安庆市怀宁县茶岭镇中心学校(246127)丁淑英

数学离不开解题,数学研究的过程就是解决问题的过程,掌握数学的一个重要标志就是善于解题[1].数学解题的目的是得出答案吗? 是,但不全是.数学解题是巩固基础知识、落实基本技能、感悟思想方法、提升思维敏锐度的系统活动,所以对一道典型问题进行多角度的分析与解答,并总结出最优最自然的解法是非常有必要的.本文是笔者对一道椭圆内伸缩三角形问题的研究,并通过该题总结出坐标形式的三角形面积公式在该类问题中的巧妙应用,现与读者分享交流.

1 试题呈现与分析

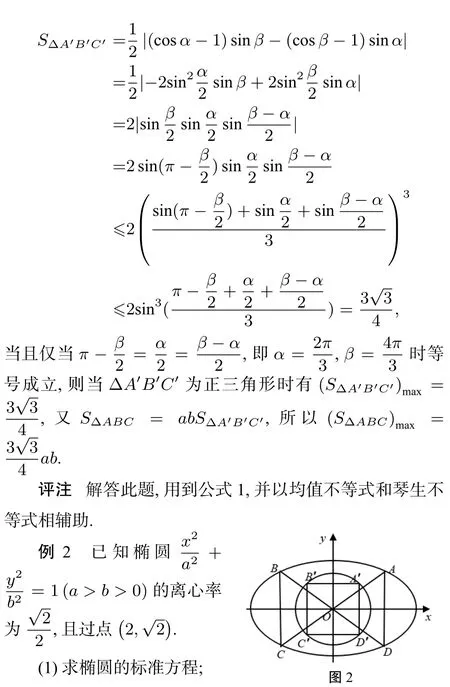
2 解法探究

3 命题的背景及公式的延伸

4 方法的提出及应用介绍

评注例4 虽不是椭圆问题, 但是通过伸缩变化, 将抛物线y2= 2px变换为y2= 4px, 使得点A(p,0)和直线x=-p为变换后抛物线的交点与准线,巧妙解题.

5 反思总结

本文通过一道椭圆内伸缩三角形面积谈起,通过坐标形式的三角形面积公式,介绍了如何利用伸缩变换达到简解一类解析几何问题的方法,该种解法虽可简化运算,巧解问题,但是尤其自身的局限性,并非通解通法,我们在日常学习中,要结合自身掌握程度和实际情况,选择最佳的解题方法,不要一味追求某一种解法,要学会从不同解法中汲取不同的数学思想,提高自身的数学核心素养[3].