模糊智能决策树模型与应用研究

鱼先锋，耿生玲

1.青海师范大学 计算机科学学院，西宁810008

2.商洛学院 数学与计算机应用学院，陕西 商洛726000

模糊决策是一门对决策信息进行推理、计算和决策的方法论，奠定了智能决策的基础。在许多决策环境下，专家往往根据他们在本领域的常识来评判一列备选方案，而在绝大多数情况下，他们的认知无法量化而只能用抽象的语言术语来表达。例如，在评估大型工程项目时，专家可能会说“这个项目在理论上基本上是好的，但是可行性有一点儿弱”。再如专家描述某工程会说，在当前阶段实施某种方案，完成工程的难度“大”或“小”。在这两个例子中，专家不可能用精确的数值来描述“基本上”“一会儿”“一点儿”“大”“小”这些词汇的精准含义，但是人们都能够理解它们所表达的意思。在许多现实的定性决策问题中，用语言术语，比如“快”的速度，“高”的价格，“低”的温度，“好”的绩效等，来表达专家的观点非常普遍而且直观易懂。然而，虽然语言术语与人们的认知非常接近，但是，语言术语的运算较复杂。1965 年Zadeh 提出了模糊集理论（fuzzy sets），1986年Atanassov 提出了模糊集理论（intuitionistic fuzzy sets）；将定性的信息定量化，来表达人们的定性决策信息。虽然决策信息的取值没有数字那么精确，但是它增强了决策信息表达的可行性、灵活性和可信度，在许多不同的研究领域取得了很好的效果。

模糊树模型在控制和决策方面取得了很多成功应用。而这些应用在树模型上或者侧重某种具体约束问题的控制策略设计，比如单输入输出系统；或者控制策略基于特定机制或策略比如自适应机制、最小Wilcoxon 学习方法等。本文根据不同的推理和决策需求，将提出不同的模糊推理规则和模糊合成规则，以刻画不同的决策过程。并将加权函数引入决策过程，刻画决策属性对决策结果的重要程度。本文将建立更具灵活性和普适性的模糊树模型。将各种推理控制策略形式化为模糊智能决策树的边，推理前提和控制信息形式化为节点，自动控制，智能选择，灵活高效，具有普适性。将工程决策问题的成本和收益形式化为边上的权值，并考虑权值偏好、决策可行性等刻画，建立了加权模糊智能决策树模型用以求解最优决策。讨论了基于模糊智能决策树做智能控制，和基于加权模糊智能决策树求最优决策方案的算法复杂度，最后结合模糊智能洗衣机控制和工程最优决策方案求解的应用实例说明文中给出的模型和算法是合理有效的。

1 模糊智能决策树

先介绍模糊数学和模糊推理的几个基本概念。

（模糊集）集合上的模糊集合（fuzzy set）是一个映射:→[0,1]，也称为模糊集合的隶属函数，常记为μ，∀∈，μ()称为属于模糊集的隶属度。模糊集合有以下几种记法：

（1）={(,())|∈}；

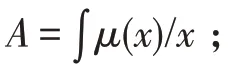
用()表示上模糊集合的全体，即()={|:→[0,1]}。

设,∈()，若∀∈有()≤()，则称含于，或包含，记作⊆。若∀∈，有()=()，称等于记作=，则((),⊆)为偏序集。

设,∈()，与的并⋃，交⋂，补A的隶属函数定义为：

(⋃)()=()∨()=max{(),()}

(⋂)()=()∧()=min{(),()}

A()=1-()

显然，若,∈()，则：

⋃,⋂,A∈()

另外，若A∈()(∈)，则可定义模糊集合的任意并与任意交的运算如下：

模糊逻辑推理是建立在模糊逻辑基础上的不确定性推理方法，是在二值逻辑三段论基础上发展起来的。这种推理方法以模糊命题为前提，动用模糊产生式规则，推导出一个近似的模糊结论。

（模糊命题）含有模糊概念、模糊数据的语句称为模糊命题。它的一般表示形式为：

其中，是模糊概念，用模糊集及隶属函数刻画；是论域上的变量，用以代表所论述对象的属性；是模糊命题的可信度。

（模糊推理）模糊产生式规则的一般形式是→(,)。其中，是用模糊命题表示的模糊条件；是用模糊命题表示的模糊结论；∈[0,1]是前提的隶属度，表示前提的可信度；∈[0,1]是推理的隶属度，表示该推理的可信程度。

（1）组合前提的不确定性计算：可采用最大最小法，当组合前提是多个单一前提的合取时，若已知(),(),…,(E)，则()=min{(),(),…,(E)}；当组合前提是多个单一前提的析取时，若已 知(),(),…,(E)，则()=max{(),(),…,(E)} ；当前提是模糊命题的否定时，(¬)=1-()。

（2）结论不确定性的更新：基于乘法原理，由产生式→(,)确定的结论的隶属度()=()·。

（3）结论不确定性的合成：由多条不同前提推出了相同的结论，但可信度不同，则用合成算法求出综合可信度。设有推理→(,)，→(,)，则据容斥原理：

依据最大隶属原则：

依据保守可信原则：

式（1）～（3）可根据实际情况选择一种即可。

当三条以上推理具有相同结论，需要合成推理时，先合成两条生成一条，再将新生成的一条与第三条进行合成，直至将所有推理合成一个。

下面给出模糊智能决策树模型。先约定∈N，决策等级标识集合（decision grade label set）={1,2,…,}。

（模糊智能决策树）模糊智能决策树模型（fuzzy intelligent decision tree，FIDT）是一个四元组,=(,,,)。其中，为叶子节点之集，记录初始决策条件，为内部节点，存储计算中间决策条件，为根节点，存储计算最终决策结果。为边集，刻画模糊决策函数。图1 给出了模糊智能决策树的框架示意图。在图1 中用圆圈表示叶子节点，用矩形表示内部节点，用圆矩形表示根节点，用箭头代表决策边集。

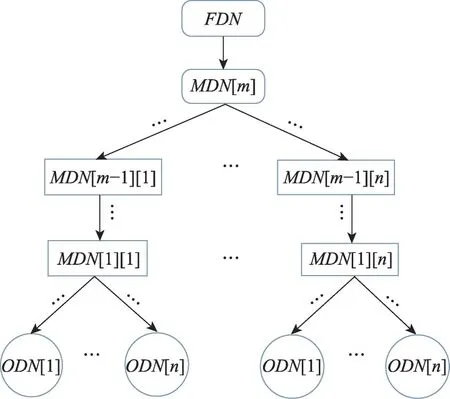
图1 模糊智能决策树框架示意图Fig.1 Frame diagram of fuzzy intelligent decision tree

中各种节点和边具体定义如下：

（叶子节点）叶子节点（original decision node）是一个三元组，=(,,)，其中：

（1）为原始决策条件的特征数量值；

（2）模糊信度函数:→[0,1]，用以原始决策条件的模糊化；

（3）一级模糊决策函数:→[0,1]对应一个指向其父节点即一个[1]的边。

（内部节点）内部节点为中间决策节点（middle decision node），是一个三元组，=(,)递归定义为：

（1）记[]∈,∈为决策树中一个第级决策节点；则[]为[]的子节点之集，递归定义为：

[]={[-1]|([-1],[])＞0}

（2）中间模糊决策函数定义为:[]→[0,1],+1 ∈，对应一个[]指向其父节点即一个[+1]的边，即[]∈[+1]刻画了决策规则，[]→[+1](,)即在[]条件的信度为([])的前提下推理到 结论[+1] 的 信 度([+1])。的具体计算已经在定义6 关于模糊推理计算的定义中给出。

（3）∀,+1 ∈递归定义，([+1])=([])。在多级推理决策中第级的结论就是第+1 级的前提。

（4）∈N，若某一决策等级有节点个，此级节点标号集合（node ordinal number set）={1,2,…,}。∀∈,∈，[][] 表示第层的第个节点。

（根节点）根节点为终级决策节点（final decision node），是一个二元组=([],,)，其中：

（1）[]为第级决策节点，记录模糊的推理结果。

（2）={,,…,ch}表示决策结果的不同等级的特征值；∀ch∈为决策结果为等的特征值。

（3）去模糊化函数:[]→，用以决策的模糊化结果[]去模糊化成一个特征函数值（一般是非负实数）。例如定义：

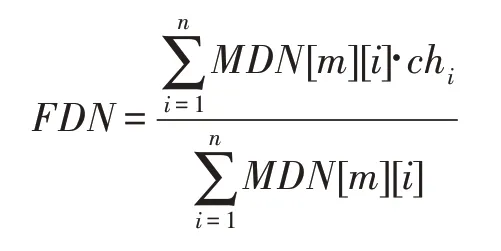
其中，[][]为决策结果为等的隶属度；ch∈为决策结果为等的特征值。

（边集）边集={,,}表示决策函数集合，其中为一级模糊决策函数，为中间模糊决策函数，为去模糊化函数。

（树高，层高）设是一个模糊智能决策树，将要做被决策对象的级决策。定义根节点所处层数为0，记为()=0；第级节点[]所处层数为-+1，记为([])=-+1；若max{([])|∈}=，则称的高度()=。

（树杈，子树）设是一个模糊智能决策树，∀[]∈，∈为决策树中一个第级决策节点，则称以[]为根节点的树记为([])，为的一棵子树。若[]的子节点之集为[]，若|[]|=∈N，则称[]节点分了叉。进一步，若在中有max{|[][]||∈,∈}=，则称为一棵叉树。

定义12 和定义13 是为了自然地参照经典树理论的术语描述的性质。经典树理论的其他概念像满叉树、完全叉树等概念也可以很容易拓展到，这里不再赘述。

（的规模）设=(,,,) 是一个叉模糊智能决策树,()=。则有：

（1）||=1,|[1]|=1；

（2）||≤n；

（3）||≤(n-1)/(-1)；

（4）||=||+||+||-1 ≤(n-1)/(-1)，边数比节点数少1。

用数学归纳法在上按层归纳得到各层节点数是关于层数的等比数列，公比为，再用等比数列求和公式很容易证得定理1 中的结论。结论中全是不等式而非等式，因为对具体决策问题生成的一般不会是满叉树，或叉完全树。

（空间复杂度）设=(,,,)是一个叉模糊智能决策树，()=。则的节点数为||+||+||，边数为||；的空间复杂度为(n。

由定理1 的结果，定理2 是显然的。

（时间复杂度）设=(,,,)是一个叉模糊智能决策树，()=。则用做智能决策需要做||+||+||次运算，的时间复杂度为(n。

决策初始在叶子节点做原始数据模糊化需要||次运算。根据定义6 和定义9 关于模糊决策算子的定义，用做智能决策需要做||次乘法求决策更新，[]=[][]⋅([][])，需做最多4(-1)||次运算求决策合成。再将定理1结果带入，就得到的时间复杂度为(n。

需要指出的是虽然的计算复杂度形式上为树杈数关于树高的指数形式(n。但庆幸的是现实中树高也就是决策等级一般比较小，≤4，大多数情况下=3 或=2。因此用做智能决策是高效的，不会出现状态爆炸。

2 加权模糊智能决策树

工程决策中要考虑成本、收益，决策者对不同成本、收益的偏好，以及不同决策方案的可行性。接下来将这些决策信息融合到决策树模型中建立加权模糊智能决策树模型，并给出基于该模型求解融合多属性信息的最优工程决策方案。

（加权模糊智能决策树）加权模糊智能决策树（weight fuzzy intelligent decision tree，）是一个二元组，=(,)。其中，=(,,,) 为模糊智能决策树，加权函数为:→，给的每一条边∈赋上一个非负实数作为边上的权值()。

（决策路径与路径可达测度）若中存在序列=[],[1][],[2][],…,[][j]满足[][j]∈[+1][j]⊂，[]∈，∈, j∈，则称为一条特征长度为的决策路径；记[0][]=[]，称：

（1）在工程决策中决策路径（定义15）和决策子树（定义13）对应着部分目标决策策略；决策通路（定义16）和对应着完整的决策策略。

（2）路径长度是边上权值之和，现实中用以刻画工程的收益（profit）或成本（cost）；当然工程决策中最优的策略应满足成本尽可能小而收益尽可能大。

（3）在有些决策问题中成本和收益在边上是钢性的或者说是分明的，比如一段工程必须花费多少钱，某个产品必然可以有多少利润；这样的话在求决策通路的加权长度时令([][j])=1；只考虑边上的绝对权值，不考虑边上的可能测度。

（决策收益与成本）记()为中所有的决策通路之集，∀∈()。()=wl()表示决策路径上的收益；()=wl()表示决策路径的成本。

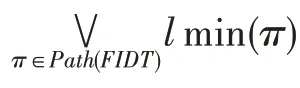
（受限决策路径）在某一工程决策中有决策要求(,)，其中，向量对(,)∈R×R，其中R表示正实数，,∈N分别表示成本和收益的种类数。若∀∈()，满足(,),记作╞(,)，当且仅当∀c∈,={1,2,…,}，(,)≤c且∀p∈,={1,2,…,}，(,)≥p。即满足(,)要求的所有种类的成本的约束。

记(,)={|∈(),╞(,)}为满足约束(,)的受限路径之集。

（收益与成本规范化）在某一工程决策中对有要求(,)，若(,)≠∅，(,)∈R×R，()=。∀∈{1,2,…,},∈{1,2,…,},∈{1,2,…,}，c表示成本的第个分量；p表示收益的第个分量；则收益与成本规范化为：

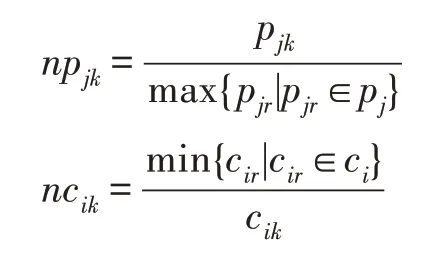
显然规范收益与收益正相关，成本与规范成本负相关；而且他们都被规范到[0,1]上。这样做有两个好处：（1）规范化数据到同一量纲，便于数据的融合；（2）这样规范化后的收益和成本沿路径累加起来可以刻画决策路径的优劣。

（最优决策路径）在某一工程决策中对有要求(,)，若(,)≠∅，(,)∈R×R，={,,…,λc}为各种成本的偏好系数，={,,…,λp}为各种收益的偏好系数；()=。∀∈{1,2,…,},∈{1,2,…,},∈{1,2,…,}，∀∈(,)，记=,[1],[2],…,[]，=[0],=[+1]，()为路径的可达测度，则关于成本的规范测度为：

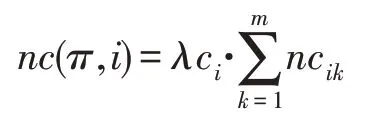
式中，nc是边([-1],[])=e∈上成本的第个分量的规范化；关于收益的规范测度为：

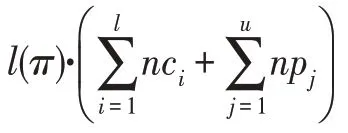
记满足(,) 的最优测度为(,)=max{(,,)|∈(,)}，这样(,)对应的路径记为(,)，即为满足(,)的最优决策路径。

求最优决策路径算法

（1）按照定义7～定义11 和定义14，从叶子节点到根节点，计算生成=(,)；节点用结构体存储，包括隶属度（前提）、信度（边即决策函数）和边上的权值（成本和收益），还有指向其父节点、子节点、兄弟节点的指针。

（2）遍历生成受限决策路径之集(,)。

①输入决策要求(,)；成本的偏好系数={,,…,λc}，收益的偏好系数={,,…,λp}；并根据定义15 确定路径测度()。

②路径标号=1，路径当前状态标号[][]=[0][0]，路径收益(π=0，路径成本cost(π=0。

③从根节点开始遍历找到最左边第一个叶子节点[]，[][]=[]。

④将[][]的所有兄弟节点依次压入栈_中。

⑤访问[][]的父节点[+1][]，计算：

若(π≤且(π≥，则++；将[+1][]添加到路径π上，若≤，执行④；否则将π添加到(,)中。

否则，若-存在[]的兄弟，从-中弹出[]的紧邻兄弟[][+1]，=+1,执行⑤。

若-不存在[]的兄弟，--,=0；若≥0,执行⑤；否则结束（2）。

（3）生成受限决策路径集的规范组合测度集合。若(,)≠∅，基于(,)中的路径，求得规范组合测度集合{(,,)|∈(,)}。

（4）在规范组合测度集合{(,,)|∈(,)}中打擂台，打出最大的元素(,)对应的∈(,)，即为(,)。

（算法复杂度）若决策问题形式化为=(,)，是一个叉加权模糊智能决策树，()=。则求解满足(,)，(,)∈R×R的最优决策路径的空间复杂度都为(lun)，时间复杂度为(lun。

空间开销在的每条边∈上多了个权重()，多出||≤(n-1)/(-1)个空间，故空间复杂度为(lun)。在中的决策通路与叶子节点一一对应|()|=||≤n，每条通路特征长度为。求(,)是要计算每条路径的收益和成本需要做4次乘法，2(-1)次加法，复杂度为(n；基于(,)求规范组合测度集合要做规范化，复杂度为(lun；求(,)需要打擂台，复杂度为|(,)|≤|()|=||≤n。因此算法时间复杂度为(lun。

3 决策实例

下面给出基于的智能决策和基于最优决策求解的应用实例。

3.1 基于FIDT 的智能决策

将应用到洗衣机的智能控制中。模糊智能洗衣机可以根据洗涤物的种类、污泥和油脂程度来自动选定洗涤时长与旋转强度。选取污泥含量、油脂含量作为决策属性；洗涤时间作为控制信息，定义输入输出量的隶属度函数并建立模糊规则。

洗衣机通过借助光度传感器来检测冲洗用水透明度的方法，测出冲洗水中污泥含量∈[0,100](%)和油脂含量∈[0,100](%)。根据污泥含量与油脂含量的检测数据，来确定洗涤时间∈[0,80](min)。用叶子节点[1]表示污泥，[2]表示油脂。根据生活经验，可将污泥含量的程度分为污泥少（SN）、污泥中（MN）和污泥（LN），并将其涵盖于的论域[0,100]，其隶属度函数如图2给出了污泥含量[0,100](%)对“SN”“MN”“LN”3 个等级的隶属度的一种定义；由图知若污泥含量为65%，则隶属度为：

图2 污泥含量对各等级的隶属度曲线Fig.2 Membership curve of sludge content to each grade

如图3 给出了油脂含量0%～100%对“油脂少（SZ）”“油脂中（MZ）”“油脂多（LZ）”的隶属度的一种定义；由图知若当前油脂含量为40%，则其隶属度为：

图3 油脂含量对各等级的隶属度曲线Fig.3 Membership curve of grease content to each grade

[][]，∈{1,2},∈{1,2,3}表示决策属性对等级的隶属度所对应叶子节点，例如[2][3]刻画油脂含量为油脂多。

洗涤时长划分为很短（TVS）、较短（TS）、适中（TM）、较长（TL）和很长（TVL）5 个等级。表1 定义了一种不同污泥含量和油脂含量等级组合下需要洗涤时长等级的分明推理规则。9 条推理规则对应9 个1 级内部节点和18 条边。比如第4 条“ 4.∧→”对应图4 所示的一棵决策子树。

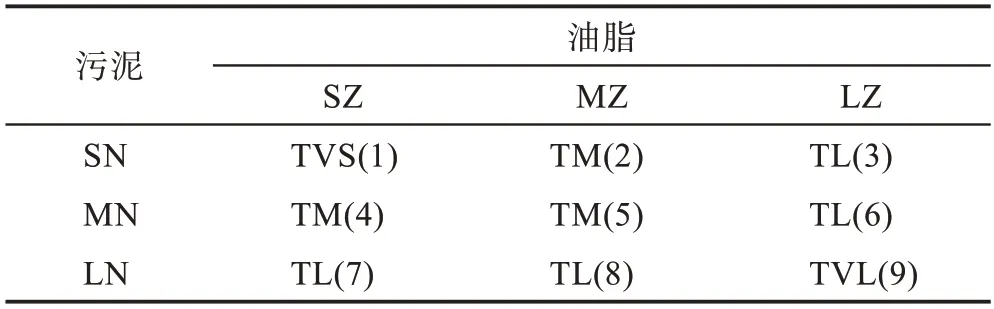
表1 模糊合成推理规则库Table 1 Rule base of fuzzy synthetic reasoning

图4 TM(4)对应的决策子树Fig.4 Decision tree corresponding to TM(4)

TM(4)形式化为([1][2],[2][1])=[1][4]。

由于污泥（65%）对SN，油脂（40%）对LZ 的隶属度为0，表1 规则库中的SN 行和LZ 列不被激活。激活规则如表2 所列。

表2 被激活规则Table 2 Activated rules

实际上决策树中有4 个1 级内部节点，8 条1 级边，8 个叶子节点。这一结果直观地体现了定理1 中的结论全是不等式而非等式，因为对具体决策问题生成的一般不会是满叉树，或叉完全树。

由表2 知有如下4 条规则被激活：

（4）∧→

（5）∧→

（7）∧→

（8）∧→

由于规则条件中连接两个条件（2 个叶子）的是“且”，在此选用取最小值法确定4 条规则（8 条边1 级边）的强度：

规则4：污泥对MN 隶属度为0.70，油脂对SZ 隶属度为0.20，min(0.70,0.20)=0.20。

规则5：污泥对MN 隶属度为0.70，油脂对MZ 隶属度为0.80，min(0.70,0.80)=0.70。

规则7：污泥对LN 隶属度为0.30，油脂对SZ 隶属度为0.20，min(0.30,0.20)=0.20。

规则8：污泥对LN 隶属度为0.30，油脂对MZ 隶属度为0.80，min(0.30,0.80)=0.30。

规则4 和规则5 的结论都为TM,根据定义6 的式（1）按容斥原理合称为：

0.2+0.7-0.2×0.7=0.76

结论为洗涤时间适中的隶属度最终为0.76，同理可得结论为洗涤时间较长的隶属度最终为0.44。这就生成了2 级决策节点[2][2],[2][3]，分别刻画洗涤时间为中和洗涤时间为长，[2][1]没有在此决策问题中出现。

表3 将各洗涤时长等级映射到一个具体的时长。

表3 洗涤等级的特征函数Table 3 Characteristic function of washing grade

根据定义10 对终极决策信息的定义，

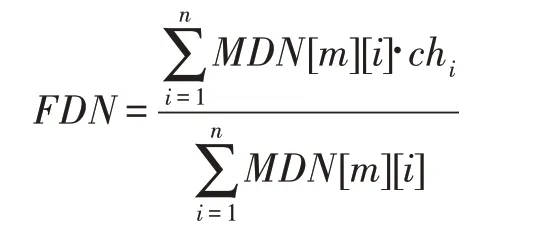
计算最终洗涤时长（单位min）输出如下：

因为38.6 ≥5，所以当污泥含量65%，油脂含量40%，智能洗衣机将自动洗涤约38.6 min；38.6 min 后智能洗衣机将再次获取彼时污泥含量和油脂含量进入下一周期模糊控制洗衣。

3.2 基于WFIDT 最优决策求解

某公司计划把一种新产品投放市场，公司管理者希望能尽快地推出该新产品以抢占市场。设有4个没有时间重叠的阶段没有完成，包括正以正常速度进行的研究工作（第一阶段）。然而，每个阶段的实施水平可以从正常水平提高为优先水平或应急水平，使之能够加速完成，而且最后3 个阶段都可以考虑提高实施水平。第一阶段可以以正常速度完成，也可以加速完成。正常、优先、应急标记为、、。管理层现在预计给研究、研制、制造系统设计、开始生产和分销这4 个阶段标记为、、、；拨款3 000 万人民币，尽量在11 个月内推出产品，还要尽可能地确保质量问题。

不同工程进度水平下4 个阶段完成所需要的时间列在表4 中。各阶段预计费用在表5 中给出。各阶段完成的可能性（隶属度）在表6 中给出。

表4 不同水平下4 个阶段完成所需时间Table 4 Time required for completion of 4 stages at different levels

表5 不同水平下各阶段预计费用Table 5 Estimated cost of each stage at different levels

公司决策者希望确定这4个阶段各自应该采取哪一种水平，同时在3 000 万人民币的预算内在11 个月内尽可能高质量地确保该产品推出市场。

3.2.2 问题形式化为

将上述决策问题的条件形式化为一个=(,)。约定∈{1,2,3,4}，对应阶段、、、；∈{1,2,3}对应水平、、；则[][i]表示中第∈{1,2,3,4}层的一个节点，表示当状态是阶段，通过实施水平后到达+1 阶段的可能性为[][i] 。例如[2][2] 表示现在在“研制”阶段，且“优先”水平进入“制造系统设计”阶段的可能，由表6 知，[2][2]=0.70。

表6 不同水平下各阶段完成可能性Table 6 Completion possibility of each stage under different levels

此决策问题初始数据为不同水平下各阶段完成可能性，已经是模糊数，不需要进行模糊化，因此不需要形式化叶子节点。另外约定根节点为表示工程完成的状态。

([][i],[+1][(+1)])表示从段实施水平后到达+1 阶段的花费；([][i],[+1][(+1)])表示从段实施水平后到达+1阶段的时间；例如([2][2],[3][3])=600；([2][2],[3][3])=3。

决策要求为：

在此问题中认为推理信度即边的可能测度为表6 中不同水平下各阶段完成可能性；∀([][i],[+1][(+1)])=∈,()，表示在第阶段实施水平进入+1阶段的可能测度；比如([2][2],[3][3])=0.70 表示当前的“研制阶段”实施“优先水平”可以完成进入“制造系统设计”阶段的可能性为0.70。为了书写简单进一步将[][i]简记为v。设决策者对时间和费用的偏好=(0.6,0.4)是指相对费用决策者更希望付出时间。

基于上述形式化的用求最优决策路径算法求得，(,)包含以下5 条路径：

显然(,)=(,,)=1.321 最大，因此决策路径为最优策略。

=,,,,；解码后对应策略为，在阶段“研究”“研制”“制造系统设计”“开始生产和分销”分别选择实施水平“加急”“优先”“优先”“加急”。现对这一结果分析如下：

（1）虽然各种满足策略消耗费用同为3 000，时间除了(,)=10，其他为11；没选做最优策略是因为算法考虑了路径上的可达测度，保守可达测度最大为0.70。

（2）虽然和的规范费用最大为0.833，但规范时间最大为1.220，且相对费用成本决策者更愿意花费时间成本：

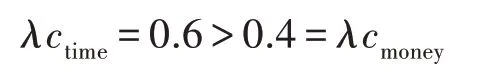
故而没选和选了。

（3）综上基于的最优策略考虑可达性、成本、收益、偏好等众多因素对决策的影响，求解结果客观合理。

4 小结与展望

基于模糊数学理论建立了一个普适的模糊智能决策树模型。用节点刻画决策信息，用树上的边记录决策控制推理规则；并在节点和边上定义合理的模糊决策算子。讨论了该模型的计算复杂度。将工程成本和收益作为权值，将不同成本、收益的偏好要求以及不同决策方案的可行性等信息进行融合作为决策方案优劣的测度。建立加权模糊智能决策模型，并给出了基于该模型求最优的多属性受限决策的算法。讨论算法的复杂度。最后结合模糊智能洗衣机控制和工程最优决策方案求解的应用实例说明文中给出的模型和算法是合理有效的。

建立的模型决策过程考虑定性与定量信息，更加客观自然且自动化程度高；决策结果科学合理且信息量大。不同决策指标建立的不同指标体系框架，都可以灵活高效地形式化为一个。将工程成本和收益作为权值，将不同成本、收益的偏好要求以及不同决策方案的可行性等信息进行融合作为决策方案优劣的测度，客观合理。后续研究工作将考虑将和用于其他背景下的智能控制与决策建模。考虑在的决策算子中添加其他一些模糊计算和模糊控制算子，使得扩充后的模型可以更灵活高效地做模糊智能决策和控制。