综合管廊燃气爆炸冲击波压力及动态响应研究

赵奇 张杨

山东建筑大学交通工程学院 济南250101

引言

综合管廊作为城市新兴的地下建筑物，正在被广泛地应用于城市建设中并日益成为便民生活的重要保障。根据中国燃气行业官方网站统计，截止2017年6月，我国共发生389起燃气爆炸安全事故，其中城市居民小区内燃气爆炸事故249起，占比64%，饭店、商户燃爆事故近90起，占比23%，因施工导致破坏燃气管道事故高达116起［1］。随着目前城市综合管廊的兴起，管廊内燃气输送管道发生爆炸的安全隐患不容小视，加强综合管廊燃气爆炸的研究刻不容缓［2］［3］。张秀华等学者研究了室内燃气爆炸冲击波的特性及传播规律［4］，燃气爆炸荷载作用下钢框架冲击响应［5］以及室内燃气爆炸作用下钢框架结构连续倒塌［6］，郭文军等学者研究了民用建筑结构燃爆事故及防灾措施［7］。程浩力等学者对管道燃气爆炸特性试验进行了研究［8］。虽然国内外学者对建筑物的抗爆性能研究较为广泛深入，但对于城市综合管廊的研究还较少，本文使用ANSYS／LSDYNA软件建立甲烷-空气混合气体在管廊内爆炸模型，进而对综合管廊进行燃气爆炸冲击荷载作用下的动力响应分析，具有重要的实际意义，可为城市综合管廊的抗爆设计提供一定的理论参考。

1 模型材料参数

1.1 钢筋混凝土材料参数

钢筋和混凝土材料均使用等向随动强化模型，其应变率效应采用Cowper-Symonds模型来计算。钢筋及混凝土材料参数见表1。

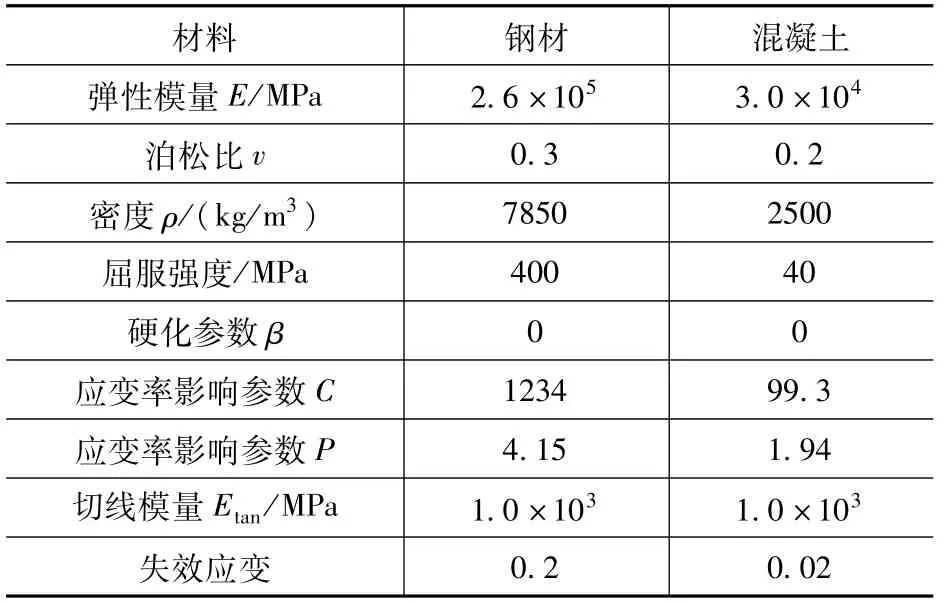
表1 钢筋、混凝土材料参数表Tab.1 Steel bar，concrete material parameter table

1.2 甲烷浓度及甲烷-空气混合气体材料

甲烷-空气混合气体爆炸时，空气中的氮气、氧气等成分比例不同会导致计算结果的差异。由田贯三、淦家平等多位学者的试验结果及理论分析可知，甲烷与空气体积比为9.5%时，爆炸产生的冲击最大［9-10］。因此，本次计算选用甲烷在空气中的浓度为9.5%。

本文选用LS-DYNA程序材料库中的气体材料模型MAT_NULL和线性状态方程EOS_LINEAR_POLYNOMIAL模拟气体材料。由于燃气爆炸产生的冲击荷载持续时间短，可将空气气体材料视为理想气体，将冲击波视为理想绝热过程；气体的线性多项式状态方程为：

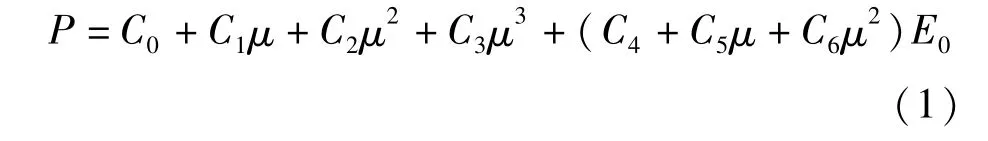
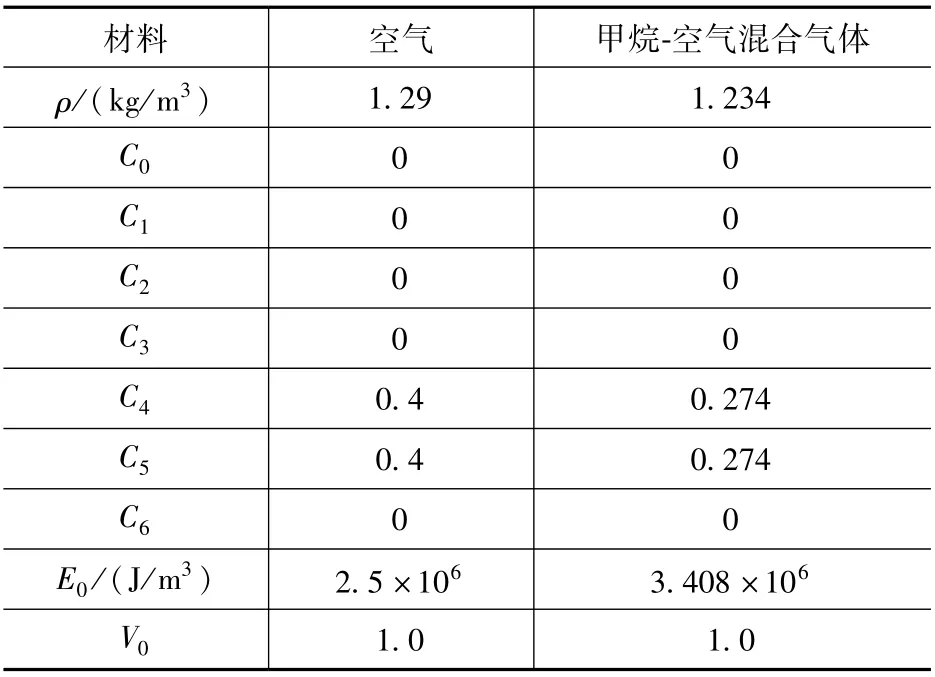
表2 两种气体状态方程参数表Tab.2 Linear polynomial equation of state parameter table

2 不同工况模型的建立

2.1 有限元模型

前处理模块采用ANSYS软件建立某管廊内甲烷-空气混合气体不同体积的爆炸模型，采用流固耦合算法进行求解计算。建立的有限元模型，净高2.8m，净宽3m，顶板、侧墙及底板厚度均为25cm，在综合管廊铺设方向每4m为一节段，取其中一节段，空气、混凝土、甲烷-空气混合气体均选用Solid164实体单元，为满足计算精度要求，模型中空气及甲烷-空气混合气体单元网格尺寸划分为10cm×10cm×10cm，混凝土单元网格尺寸划分为10cm×10cm×5cm。为突出研究重点，简化计算模型，本次研究忽略模型自重，且忽略管廊四周覆土压力和约束。因甲烷-空气混合气体密度较小，故建模时将其设置在管廊内上方。模型如图1、图2所示。

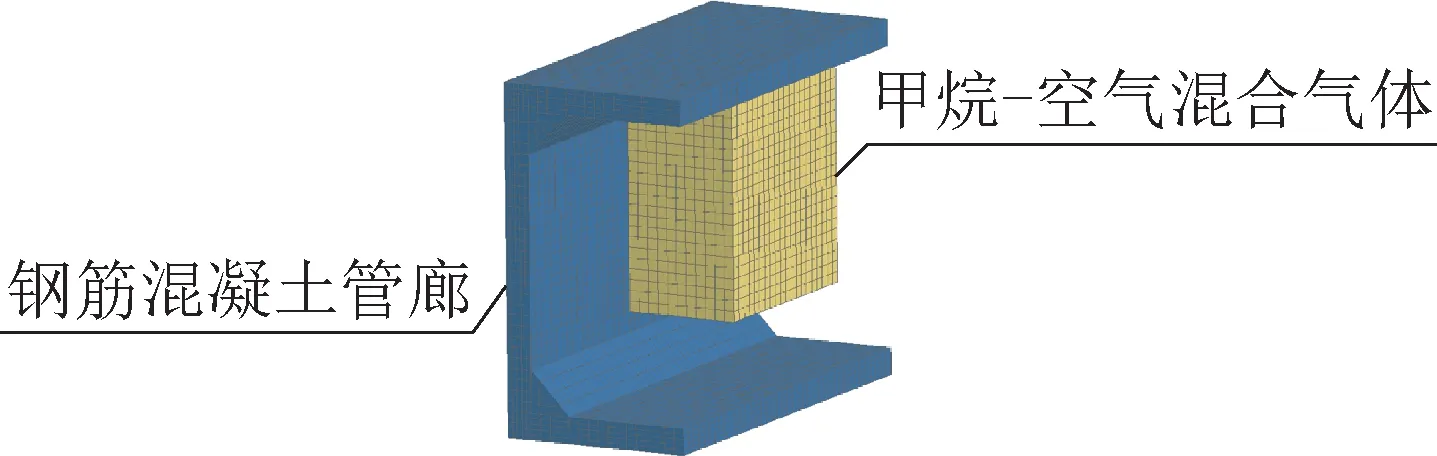
图1 模型图Fig.1 Model

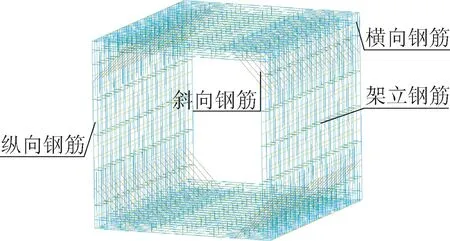
图2 钢筋图Fig.2 Bar graph

2.2 计算工况

本文研究中，对同一管廊内不同体积燃气进行有限元数值模拟，燃气尺寸见表3。

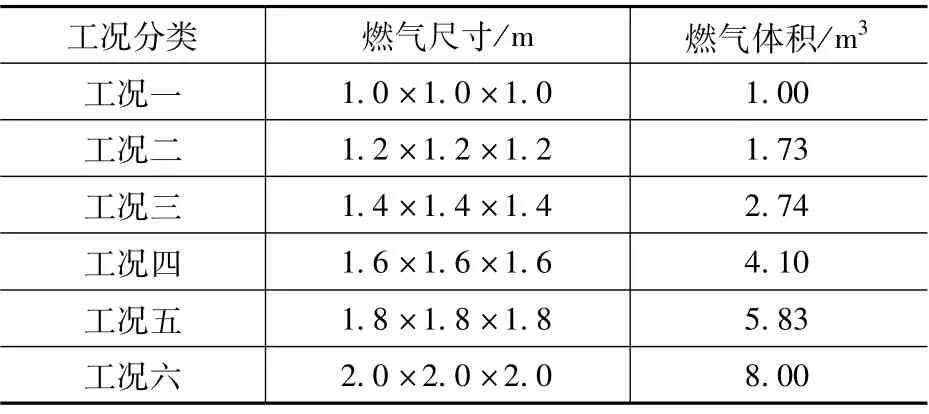
表3 6种燃气体积工况表Tab.3 Working condition

3 有限元模型计算结果

3.1 空气冲击波压力

1.以工况一X方向为例

将空气模型沿YOZ面和XOY面分割，取四分之一空气单元分析，沿X方向选取空气单元如图3所示。

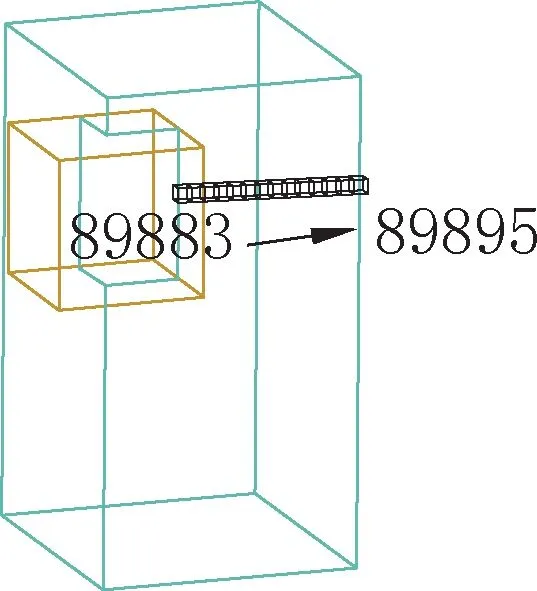
图3 X方向单元位置示意图Fig.3 Diagram of unit position in X direction

提取空气单元的超压时程曲线，汇总后见表4，距离甲烷-空气混合气体最近的空气单元达到峰值的时间最短，峰值最大，X、Y、Z三个方向的值分别为0.632MPa、0.640MPa和0.653MPa；随着距离的增加，选取的空气单元达到峰值用时更长，且峰值逐渐降低。

表4 沿X方向选取空气单元的超压峰值Tab.4 Select the overpressure peak value of the air unit along the X direction

2.空气冲击波超压峰值曲线拟合

使用Origin软件，画出散点图，并拟合曲线如图4所示，方程形式为y=A1×exp（-x／t1）+y0。

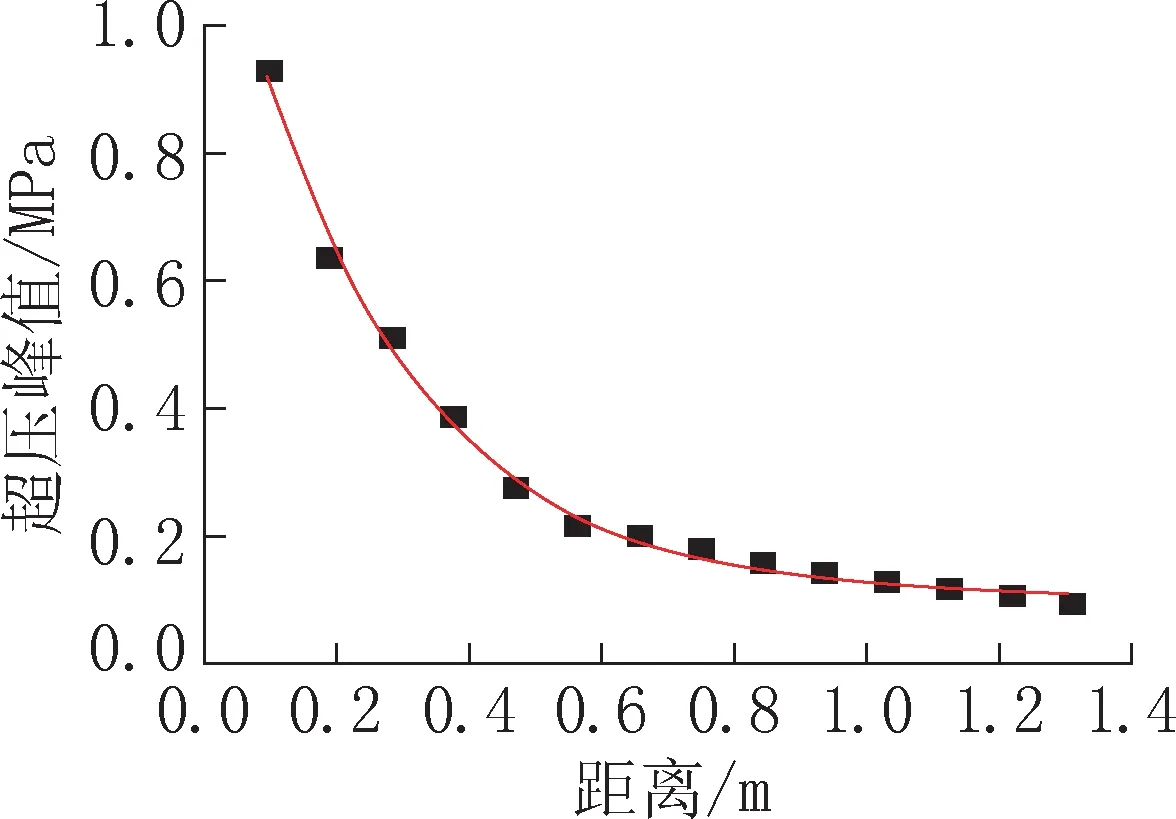
图4 工况一距离-空气冲击波峰值散点图Fig.4 Working condition a distance-air shock wave peak scatter diagram

本文探究问题为气相爆炸，与点源爆炸形成的理想球状冲击波不同，爆炸后不同时刻冲击波波阵面内各点的峰值压力不同，因此本文分别取甲烷-空气混合气体边缘等距离的空气单元展开研究，即上文所示沿坐标轴等距离的空气单元，将距离相同的三个空气单元的超压峰值取均值分析。使用Origin软件中Levenberg-Marquardt优化算法拟合，拟合结果见表5。

3.2 空气冲击峰值曲面

提取6个工况的空气冲击波超压峰值曲线，可知在燃气爆炸发生时，空气冲击波超压峰值均小于0.7MPa，且随着甲烷-空气混合气体体积的增加，空气冲击波超压峰值衰减的趋势逐渐减弱，如图5所示。根据各工况拟合的曲线进行整理分析，提出关于以燃气边缘距离和燃气体积为变量的空气冲击波峰值曲面数学解析式。

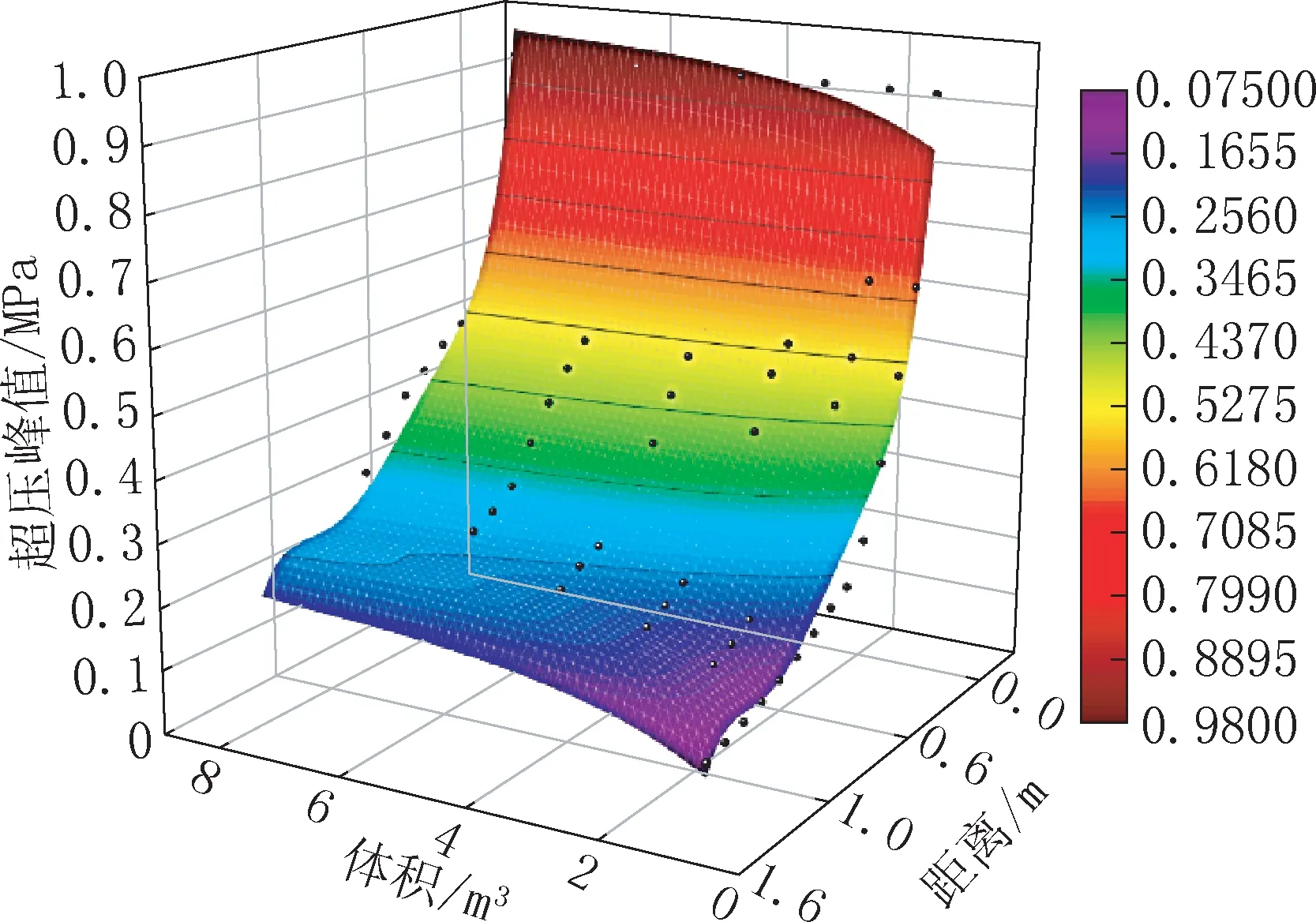
图5 X、Y、Z方向关于距离、燃气体积空气冲击波峰值散点图Fig.5 X，Y，Z direction on the distance，volume of gas air shock wave peak scatter diagram

数学解析式：

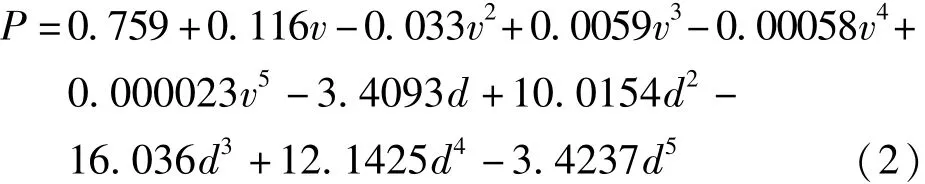
4 曲面公式应用分析

4.1 应用空气冲击峰值曲面模拟加载

当燃气体积v=8m3时，底板d=0.8m、侧墙d=0.5m、顶板d=0.1m处计算得空气冲击波超压峰值分别为0.30MPa、0.42MPa、0.71MPa。在综合管廊有限元模型内壁四个方向施加简化的燃气爆炸荷载曲线，对结果进行对比分析，加载位置如图6所示。

图6 管廊内加载位置Fig.6 Loading position in pipe gallery

在整体式综合管廊有限元模型内壁施加简化的三角形冲击荷载曲线，分别在顶板、侧墙、底板内侧施加动荷载曲线分别为荷载曲线1、荷载曲线2和荷载曲线3。加载燃气爆炸动荷载曲线如图7所示，荷载曲线压力开始时间t0的确定以底板d=0.8m处施加荷载曲线3为例，，同理荷载曲线1、荷载曲线2压力开始时间分别为0μs、269μs。动载曲线荷载曲线1、荷载曲线2、荷载曲线3到达峰值的时间tm分别为300μs、950μs、1350μs。

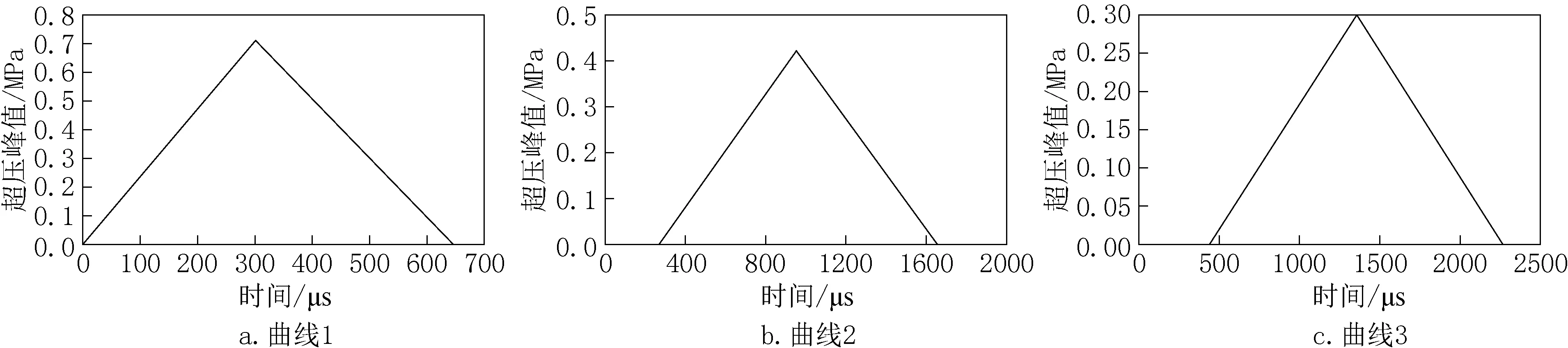
图7 管廊内壁加载简化三角形冲击荷载曲线Fig.7 The simplified triangle gas explosion load curve of pipe rack loading

顶板荷载曲线1持续时间：

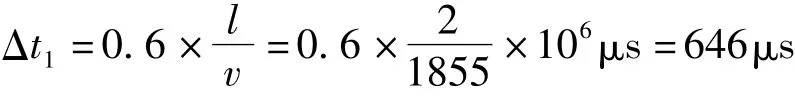
侧墙荷载曲线2持续时间：

底板荷载曲线3持续时间：

4.2 峰值对比

采用流固耦合算法和应用本文提出的峰值曲面公式和在综合管廊内壁直接施加冲击荷载的方法，二者数值模拟的峰值对比分析见表6。

5 结论

本次研究采用ANSYS／LS-DYNA有限元分析软件，采用流固耦合算法以整体式综合管廊为研究对象，选取不同甲烷-空气混合气体单元体积建立6种工况，分别对不同工况下爆炸产生的冲击波峰值压力进行采集、整理并分析，得到6种工况下距离甲烷-空气混合气体单元边缘不同间距的爆炸冲击波压力峰值曲线，汇总整理不同混合气体体积下、距混合气体体积边缘不同距离的爆炸冲击波压力峰值曲线，进行曲面拟合，得到管廊内不同甲烷-空气混合气体体积下、距混合气体体积边缘不同距离的爆炸冲击波压力峰值曲面的数学解析式。

通过采用爆炸冲击波压力峰值曲面公式和在综合管廊顶板、底板和侧墙内侧直接施加动载曲线相结合的方法，模拟甲烷-空气混合气体爆炸冲击荷载，能够有效缩短计算时间，且本文提出的应用峰值曲面公式法与流固耦合算法在计算管廊的节点峰值位移、混凝土单元峰值应力、钢筋轴向及Mises应力峰值时结果相差最大为8.6%，均不超过10%，可以满足工程实践的要求。

通过对管廊的顶板、底板和侧墙等部位的节点位移和混凝土单元各方向及有效应力分析可知，距离爆炸最近的顶板在发生燃气爆炸时所受到的爆炸冲击最严重，顶板节点发生较大的竖向位移且顶板内外侧混凝土单元产生较大的应力峰值，表现为“撕裂损伤”。通过对横向、纵向钢筋进行应力分析可知，钢筋的拉应力最大值均低于200MPa，应力峰值均小于钢筋屈服应力，但如果考虑恒载作用下的拉应力叠加，则钢筋总应力不能超出设计强度，因此在配筋时需考虑由爆炸荷载引起钢筋的应力增长。