碳纤维双马树脂基圆锥壳的热振动特性研究1)

郑博文 赵 锐 于开平

(哈尔滨工业大学航天学院，哈尔滨 150001)

高速飞行器以高马赫数飞行时，面临着极其严酷的高温环境，高温会显著改变其振动特性，进一步引起颤振特性的变化[1-3]。高温对飞行器弹性性能的影响体现在两个方面：(1)引起材料的弹性模量变化，通常表现为弹性模量降低；(2) 使结构内部出现热应力，改变结构的刚度大小以及分布。通常而言，高温会降低飞行器的结构刚度，表现为固有频率随温度升高而减小。

热振联合试验通过在地面上模拟高温环境，对结构的高温振动特性进行研究[4]。吴大方等[5-10]和Wu 等[11]在热振联合试验系统的基础上，通过耐高温引伸杆将信号传递到高温区外部测量，完成了翼面结构的热模态试验，并不断突破热模态试验和热振试验的温度上限至1200°C 与1500°C。基于激光测振仪的非接触式振动信号测量，刘浩等[12-14]探索了热模态试验中的模态参数辨识方法。谭光辉等[15]研究了钛合金翼面的固有频率在不同温度环境中的温升变化规律。唐晓峰等[16-17]利用多个激光测振仪的同步测量，给出了细长体飞行器和轴承支撑的舵面在高温环境下的模态频率与振型。程昊等[18]完成了铝合金壁板在热屈曲前后的热模态试验，发现以屈曲温度为转折点，壁板的固有频率先随温度升高而减小，后随温度升高而增大。于开平等[19]研究了C/SiC 箱型结构在1000°C 以下模态特性。Gao等[20]研究了C/SiC 组装结构在高温环境中的模态特性，并探索了FBG 传感器在热模态试验中用作温度和应变测量的可能性。FBG 传感器的优势在于同时完成振动与温度的测量，但是试验过程中存在脱落的风险。

有限元方法是研究结构在高温环境中的振动特性的有效方法，能对热模态试验的结果进行深入解释。贺尔铭等[21]以有限元方法分析了二维正交编织C/SiC 壁板在温升过程中出现的模态交叉和丢失现象。Zhang 等[22]在碳纤维增强莫来石三明治结构的热模态试验基础上，用有限元方法研究了面板材料参数、夹芯材料参数以及热应力在温升过程中对结构振动特性的影响。Cheng 等[23]在非均匀温度场中进行了平板的热模态试验，结合有限元分析表明，面内非均匀温度场引起平板的刚度分布不均匀，导致其固有频率随温度升高而增大，以及模态交叉现象的出现。白云鹤等[24]和Bai 等[25]对复合材料蜂窝板在发生损伤前后的热模态试验进行了研究，并用有限元方法对试验结果进行了解释。Silva 等[26]将全场测量应用于非均匀温度场的热模态试验中，结合有限元方法，分析了温度对于平板热模态的影响方式。Zhang 等[27]将DIC 用于热屈曲温度的预测，并以热模态试验得到了C/SiC 板在热屈曲前后的温升变化规律。基于屈曲后的试验结果，用有限元方法研究了具有不同材料参数、板厚度和边界条件的屈曲后C/SiC 板的热模态。

尽管关于结构在高温环境中的振动特性研究已经很多，但是试验对象大多是翼面、舵面、壁板、三明治板和蜂窝板等二维结构，少有三维结构。因此，有必要进一步研究三维立体结构在高温环境中的振动特性。本文的试验对象是一种碳纤维双马树脂基圆锥壳。以类圆筒形加热阵列模拟高温环境，对自由边界的圆锥壳进行热模态试验，获得圆锥壳的热振动特性。结合有限元模型修正方法建立有限元模型，研究温度对圆锥壳的热振动特性的影响机理以及圆锥壳热应力的成因和影响因素。

1 热模态试验与分析

1.1 热模态试验

试验件是一种碳纤维双马树脂基圆锥壳，采用层合板制成，铺层为[45/0/0/-45/0/-45/0/0/90]s。圆锥壳的长度为400 mm，顶面直径为380 mm，底面直径为400 mm，厚度为2.4 mm。

热模态试验的装置如图1 和图2 所示，考虑到圆锥壳的曲面结构，为其提供高温环境的石英灯呈圆筒形排列。由于圆锥壳的上下底面直径不同，对石英灯进行调整，令其与圆锥壳的曲面平行。热电偶在圆锥壳的内外表面均粘贴一个，分别测量加热面(外表面) 和非加热面(内表面) 的温度。本试验采用耐高温绳将圆锥壳悬挂，以达到模拟自由边界条件的目的。激励方式为随机脉冲序列激励方法，将激振杆穿过加热设备之间的空隙，与圆锥壳之间保持适当的距离，令激振器能够提供脉冲激励。为了让力传感器不受高温影响，远离加热区，将其安装在激振杆和激振器之间。振动信号测量设备为激光测振仪，该设备在远离加热区的位置进行非接触测量，既不会产生附加刚度和附加质量影响，又能够避免高温对设备的影响。受加热设备的遮挡影响，无法在加热过程中对圆锥壳进行多点测量，而是进行了单点测量。模态试验在室温，100°C，150°C，200°C 和250°C 下进行，温度曲线如图3 所示。先将圆锥壳以较慢的温升速率加热到50°C，并恒温10 s；然后以每秒1°C的速率对圆锥壳进行加热，并在上述的试验温度恒温一段时间以后进行模态试验。图3 中，预设温度为提供的预先设置的加热曲线，外表面温度为圆锥壳外表面的实测温度，内表面温度为圆锥壳内表面的实测温度。

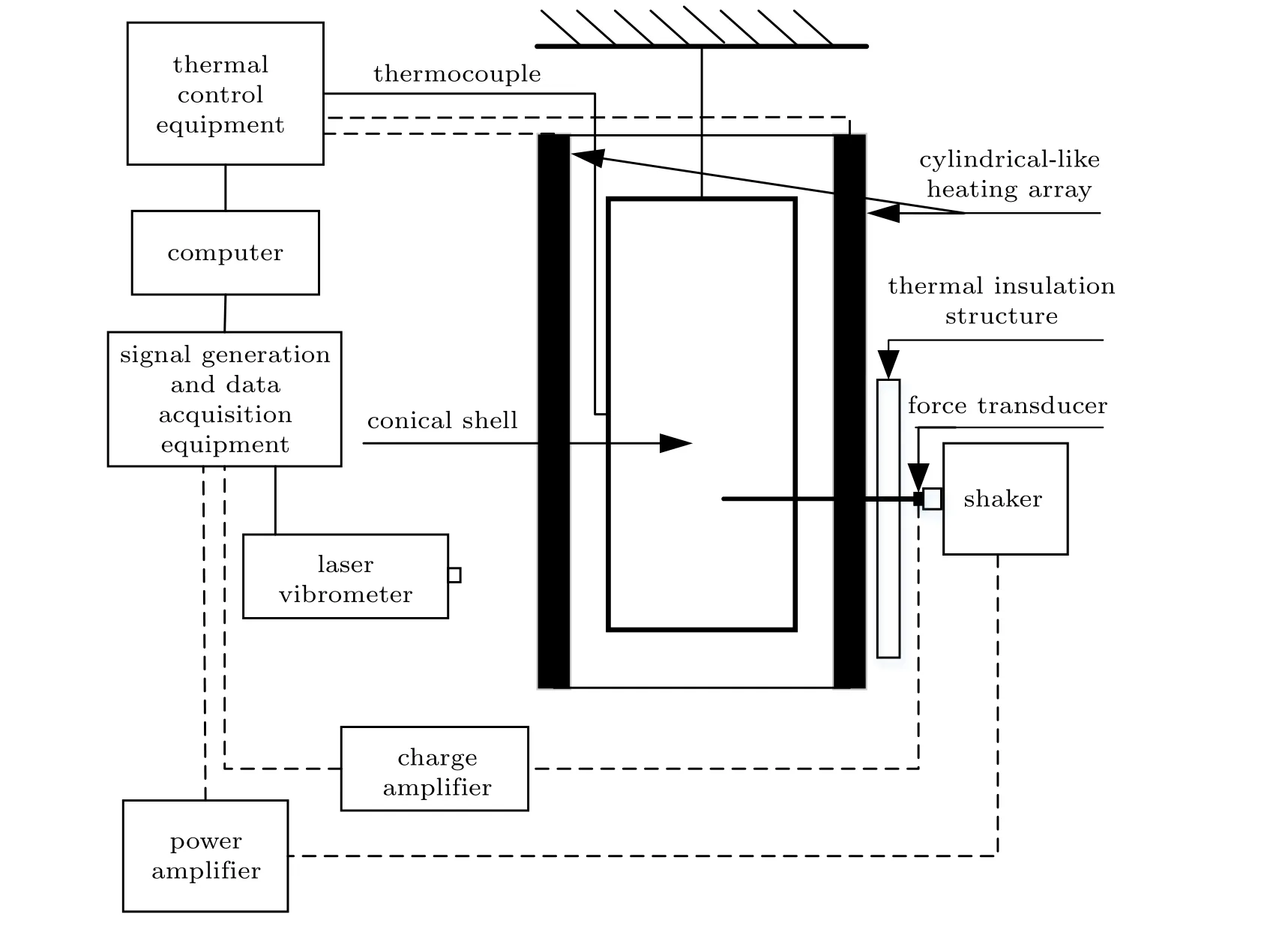
图1 热模态试验系统Fig.1 Thermal modal test system

图2 试验装置照片Fig.2 Photo of test equipment

图3 温度曲线Fig.3 Temperature curves

1.2 试验结果分析

表1 所示为圆锥壳在热环境中的前三阶固有频率。为清晰地认识圆锥壳的固有频率随温度升高的变化规律，将室温时的固有频率作为参考，计算圆锥壳的固有频率在不同温度时的变化幅度，如图4所示。从图中可知，200°C 是一个转折点，圆锥壳的固有频率在200°C 前后的变化规律发生了改变。在200°C 以前，前三阶固有频率均随温度升高而减小，且一阶固有频率减小的幅度显著大于其余固有频率。在200°C 以后，圆锥壳的三阶固有频率依然在减小，而一阶和二阶固有频率则增大了。该结果表明，圆锥壳的特性在200°C 以后发生了变化，极有可能是因高温而发生了结构损坏。试验过后，观察到圆锥壳的内表面发生了局部凸起变形(如图5 所示)，验证了圆锥壳发生结构损坏的判断。由于圆锥壳在200°C以上会发生破坏，而本文主要研究其在破坏前的热振动特性，因此下文中的最高研究温度为200°C。

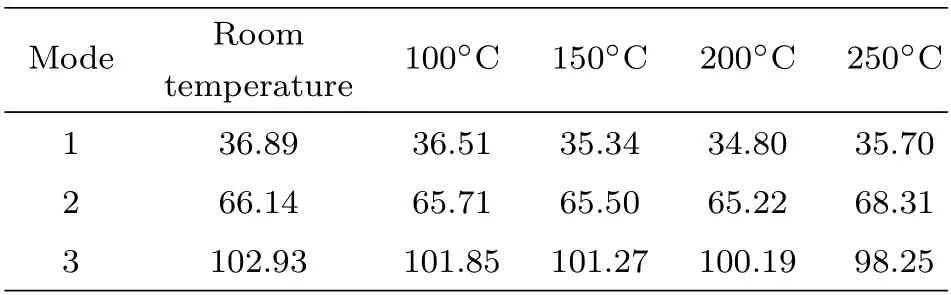
表1 圆锥壳在不同温度时的固有频率/HzTable 1 Natural frequencies of conical shell at different temperature/Hz

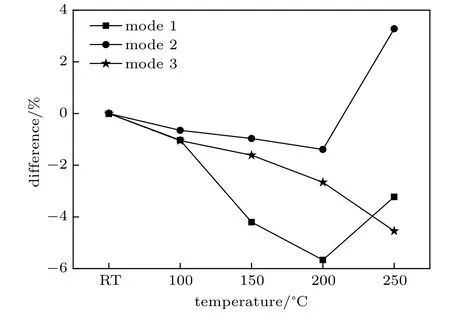
图4 固有频率相比室温的变化幅度Fig.4 Difference of natural frequency compared with that at room temperature

图5 热模态试验后的圆锥壳(内表面局部凸起)Fig.5 Conical shell after thermal modal test (local convexity of inner surface)

2 有限元分析

2.1 有限元建模与模型修正

本文中采用的有限元分析软件为Abaqus。首先根据圆锥壳的几何尺寸构建一个长度为400 mm，顶面直径为380 mm，底面直径为400 mm 的几何结构，然后将其划分4920 个单元(单元尺寸为10 mm)，有限单元为壳单元S4R。材料属性方面，采用层合板理论对圆锥壳进行有限元建模，铺层为[45/0/0/-45/0/-45/0/0/90]s，单层的材料参数如表2 所示。其中，密度ρ，泊松比ν12，拉伸模量E11和拉伸模量E22由标准实验获得。但是，剪切模量G12，剪切模量G13，剪切模量G23，线膨胀系数α11和线膨胀系数α22并未由标准试验得到。因此在初始有限元建模中，根据工程经验进行赋值，并将其作为待修正参数，后续采用模型修正方法对其进行修正。根据图3可知圆锥壳在不同温度下的内外表面温度，基于该温度条件对有限元模型的温度场进行赋值。圆锥壳的热模态试验在边界条件下进行，因此无需添加位移约束。采用处于室温的有限元模型进行网格无关性验证，结果如表3 所示。从表中可以看出，随着单元尺寸的减小，圆锥壳的前三阶固有频率逐渐收敛。当单元数量达到4920 以后，继续增加网格密度对前3 阶固有频率的影响很小。因此，采用10 mm 的单元尺寸将有限元模型划分成4920 个单元，可以兼顾计算速度和计算精度。最后，采用该有限元模型进行分析，可得室温和200°C 时的固有频率和模态振型如表4，表5 和图6 所示。

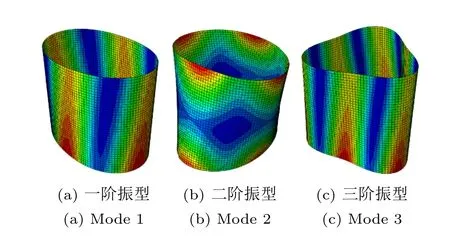
图6 前3 阶模态振型Fig.6 First three mode shapes

表2 试验件的材料参数Table 2 Material properties of test piece

表3 不同单元尺寸的仿真结果(室温)Table 3 Simulation results with different element sizes (room temperature)

表4 初始有限元分析的固有频率(室温)Table 4 Natural frequencies of initial finite element model (room temperature)

表5 初始有限元分析的固有频率(200°C)Table 5 Natural frequencies of initial finite element model (200°C)

由表4 和表5 可知，尽管有限元计算值与试验结果之间存在误差，但最大误差只有-5.72%，可见误差并不是非常大。这说明圆锥壳的初始有限元模型是合理的，能够反应圆锥壳的振动特性，但是个别参数并不准确，需要进行模型修正。考虑到剪切模量G12，剪切模量G13，剪切模量G23，线膨胀系数α11和线膨胀系数α22不是由标准实验测量得到的，因此将它们选为待修正参数。

对于碳纤维双马树脂基圆锥壳的高温动力学模型修正，分两步进行。首先对室温动力学模型进行修正，然后对200°C 时的高温动力学模型进行修正，其余温度的参数通过插值得到。该修正方法假设圆锥壳的材料参数随温度线性变化，在修正结果中需要对此进行验证。

进行室温下的有限元模型修正时不必考虑温度的影响，无需对线膨胀系数进行修正，待修正参数只有剪切模量G12，剪切模量G13和剪切模量G23。进行灵敏度分析，结果如图7 所示。由图可知，只有G12对圆锥壳的前3 阶固有频率较为敏感，G13和G23几乎不会产生影响，所以只对G12进行修正。

图7 固有频率关于剪切模量的灵敏度Fig.7 Sensitivity of natural frequency with respect to shear modulus

高温时的有限元模型修正需要考虑温度的影响，所以待修正参数为剪切模量G12，线膨胀系数α11和线膨胀系数α22，修正后的参数如表6 所示。

表6 圆锥壳修正后的参数Table 6 Updated parameters of conical shell

表7 为有限元模型修正前后的固有频率与试验值之间误差。从表中可知，经过修正以后，室温，100°C，150°C，200°C 的各阶固有频率的误差都显著降低了，有限元模型的分析结果与试验结果吻合较好。该结果表明，假设碳纤维双马树脂基圆锥壳的弹性模量随温度线性变化是可行的。尽管只对室温和200°C 的弹性模量进行修正，各温度下的仿真分析结果与试验结果吻合良好。对于修正后依然存在的误差，可能有以下几个原因：圆锥壳的制造误差、温度场不均匀、模态分析误差等。

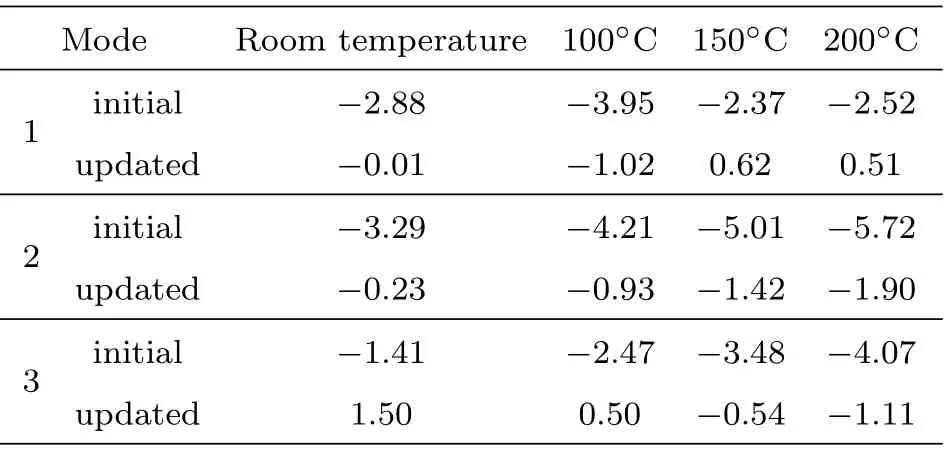
表7 有限元模型修正前后的误差/%Table 7 Error of initial and updated finite element models/%

2.2 热模态试验的仿真分析

为了研究圆锥壳的固有频率随温度升高而降低的机理，基于修正后的有限元模型，以控制变量方法，分别分析弹性模量和热应力发挥的作用。

首先考虑弹性模量的作用，在有限元分析中将线膨胀系数剔除，以排除热应力的作用。图8 显示，随着温度升高，固有频率减小。此外，由于一阶和三阶模态振型具有类似的形式，对应固有频率的变化一致，而二阶模态振型的形式不同，对应固有频率的温升变化也不相同。该结果表明，温度升高引起的弹性模量下降会降低圆锥壳的刚度，且在不同方向的作用程度不同，从而导致不同形式的模态受到的影响不同。

接着考虑热应力的作用，在有限元分析中让弹性模量一直保持室温时的数值，不随温度发生变化，从而排除弹性模量变化的影响。图9 显示，随着温度升高，固有频率增大，一阶和三阶固有频率的温升变化基本一致，二阶略有不同。该结果表明，热应力的作用是提高刚度，在不同方向上的影响差异不大。

对比图8 和图9，弹性模量变化的影响明显大于热应力的影响，因此综合二者的效果是圆锥壳的固有频率随温度升高而减小。根据以上分析可知，理想状态下，一阶固有频率和三阶固有频率的温升变化规律应该基本一致。但是，由图4 可知，试验结果并不符合该结论，说明热模态试验存在误差。

图8 固有频率仅受弹性模量影响的变化规律Fig.8 The change of natural frequencies only affected by elastic modulus

图9 固有频率仅受热应力影响的变化规律Fig.9 The change of natural frequencies only affected by thermal stresses

2.3 热应力分析

在热模态分析中，热应力是值得关注的一个重要因素。一般而言，结构受到外部约束(如边界条件)而产生的热应力会降低结构的刚度，表现为固有频率减小。结构受内部约束而产生的热应力可能发挥不同的作用。对板壳结构而言，因温度梯度引起的热应力同样起到降低结构刚度的作用，而因面内非均匀温度场引起的热应力则会导致结构刚度提高，从而出现固有频率随温度升高而增大的现象。

在上一小节中，当单独考虑热应力的作用时，圆锥壳的固有频率是随着温度升高而增大的，说明热应力增大了圆锥壳的刚度。但是此处的温度场在面内是均匀的，在厚度方向存在温度梯度，显然不符合上述规律，说明有其他原因导致了热应力的出现。由于制成圆锥壳的是各向异性复合材料，其在不同方向上的热变形是不一致的，所以各单层的变形不协调可能是导致热应力出现的原因。为了对这个猜想进行验证，分别分析两种不同条件下的热应力：(1)材料参数等与实际结构一致，采用200°C 的均匀温度场；(2)将复合材料单层的线膨胀系数改为各向同性，取值为2.657×10−7K−1，采用200°C 的均匀温度场。如表8 所示，前者在均匀温度场中依然存在热应力，后者则不存在，证明各单层的变形不协调确实会导致热应力产生。此外，热应力的最大值和最小值的差异很小，说明该热应力在圆锥壳上几乎是均匀分布的。

表8 圆锥壳在不同条件下的热应力Table 8 Thermal stresses of conical shell under different conditions

接下来进一步研究可能会对圆锥壳热应力造成影响的因素。由于热应力是因为各单层热变形不协调引起的，所以猜测铺层角度、铺层顺序会对热应力产生影响，分别采用以下3 种铺层方式进行分析验证：(1) 铺层1 为[45/0/0/-45/0/-45/0/0/90]s，与实际结构保持一致；(2)铺层2 为[90/0/0/90/0/90/0/0/90]s，将铺层1 中的45°和-45°铺层均改为90°铺层，以此考察铺层角度的影响；(3) 铺层3 为[0/0/0/0/0/45/-45/-45/90]s，将铺层1 的顺序进行了改变，以此考察铺层顺序的影响。热应力分析的温度条件均为200°C 的均匀温度场。表9 显示，同一种铺层的圆锥壳的最大最小热应力基本一致，表明热应力基本均匀分布在圆锥壳内，不同位置的差异极小。从表9 还可以观察到，不同铺层的热应力具有较大差异，证明铺层角度和铺层顺序对圆锥壳因各单层变形不协调产生的热应力具有重要影响。从该结果可知，通过铺层设计能够改变结构的热应力。

表9 表圆锥壳不同铺层的热应力Table 9 Thermal stresses of conical shell with different stacking sequences

3 结论

(1) 完成了一种碳纤维双马树脂基圆锥壳在室温，100°C，150°C，200°C 和250°C 温度环境中的热模态试验，获得了前三阶固有频率。试验结果表明：圆锥壳在200°C 以上时会出现层间分离，并发展为局部凸起，最终导致振动特性的改变。在200°C以下，圆锥壳的前三阶固有频率随着温度升高而减小。

(2)基于室温和200°C 时的热模态试验结果，对有限元模型的剪切模量G12，线膨胀系数α11，线膨胀系数α22进行了修正。经过修正以后，有限元分析得到的固有频率与试验结果吻合良好(大部分小于1%)。该结果表明：假设碳纤维双马树脂基圆锥壳的弹性模量随温度线性变化是可行的。

(3)基于修正后的有限元模型，采用控制变量法分别分析了弹性模量和热应力在固有频率随温度升高而降低时发挥的作用。分析结果表明：随着温度升高，弹性模量下降会降低刚度，引起固有频率减小；热应力则会提高刚度，引起固有频率增大。对于圆锥壳，二者综合作用会导致固有频率的下降。

(4)通过热应力分析发现，圆锥壳热应力的产生原因不是外部约束和厚度方向的温度梯度，而是碳纤维双马树脂基复合材料的热膨胀能力具有各向异性。热膨胀能力各向异性导致不同角度铺层的各单层出现热变形不协调，从而产生了热应力。该热应力在圆锥壳上几乎均匀分布，其作用是提高刚度，使固有频率增大。进一步研究表明，通过铺层设计改变铺层的角度和顺序，能够改变热应力大小。