基于核心素养，改进小学运算教学的实践与思考——以“两位数乘两位数的笔算（不进位）”教学为例

江苏邳州市运河小学（221300） 张新宇

数的运算历来是小学数学教学的重要内容，培养和发展学生的运算能力一直是小学数学教学的重要目标。长期以来，小学数学计算教学一直存在着一些问题与不足：忽视算理教学，算理与算法割裂；注重算法模仿，缺乏数学抽象，忽视算法的自我建构；等等。核心素养的培养对运算教学提出了更新更高的要求，为此，小学数学教学要彰显运算教学独特的数学育人价值，全面落实数学学科素养。下面以三年级下册“两位数乘两位数的笔算（不进位）”教学为例，谈谈笔者改进数的运算教学的实践与思考。

一、基于逻辑推理，改进算理与算法教学，实现“理法”共融

逻辑推理是学生在数学学习中应用最为广泛的一种思维方式，也是学生数学核心素养的重要内容之一。数学课程标准指出：“推理能力的发展应贯穿于整个数学学习过程中。推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。”推理一般包含合情推理和演绎推理，这两种推理都是逻辑推理。合情推理用于探索、发现结论，演绎推理用于证明结论；合情推理是一种由特殊到一般的推理，演绎推理则是一种由一般到特殊的推理。

小学运算教学运用较多的是合情推理这种逻辑推理形式，帮助学生理解算理、掌握算法。因为在计算教学中，算理是计算的基本依据，是由概念、定律、性质和实际数量关系等组成的；算法是计算的基本程序和方法。算理不清，算法不明，计算技能就难以提高。因此，理解算理、掌握算法是学生计算能力的双翼，教学中不能厚此薄彼。不仅要让学生知道该怎样算，而且还要让学生知道为什么要这样算，不能重法轻理抑或重理轻法，要让学生在理解算理的基础上掌握算法，做到“理法”共融、相互促进。

例如，教学“两位数乘两位数的笔算（不进位）”时，为贴近学生生活实际，笔者将教材例题“幼儿园购进12 箱迷你南瓜，每箱24 个。一共有多少个？”改编为“幸福路小学运来12箱牛奶，每箱14盒。一共有多少盒？”。笔者带着学生经历三次从算理理解向算法过渡的逻辑推理过程：第一次，引导学生观察教学情境图，找到直观算法，即先算10 箱牛奶的盒数（14×10=140），再算2 箱牛奶的盒数（14×2=28），最后算12 箱牛奶的盒数（140+28=168）。第二次，引导学生推理。用画“圆圈图”（每一个圆圈代表一盒牛奶，每一行14 个圆圈代表一箱牛奶的盒数，一共有12行，代表12箱牛奶的箱数）的方法，直观表示第一次得到的算法中每一步算式表示的意义，实现直观算理向算法的过渡。第三次，在借助数量关系、直观模型的基础上向竖式原理迈进。通过推理，把上面的分步算式或“圆圈图”中圈出的部分组装起来，就变成了两位数乘两位数的竖式笔算方法（先用第二个乘数的个位乘第一个乘数，再用第二个乘数的十位乘第一个乘数，最后把两次乘得的数相加）。这样，通过层层递进的逻辑推理活动，实现从算理理解到算法掌握的融通，达到水到渠成的效果。

二、基于数学抽象，改进算法建构，实现自我构建

数学核心素养的建立，必须体现数学学科的本质。能体现数学学科本质的无疑是数学的基本思想——抽象、推理和模型。数学抽象作为数学核心素养的重要组成部分，其独特的育人价值在于让学生学习如何从数学的角度去认识周围的事物。数学课程标准和建构主义理论都强调在学生的计算过程中要引导学生经历、体验算法的形成过程，让学生在直接经验的基础上，通过数学抽象概括出一般意义的算法。

1.利用学生已有经验，展开数学抽象

计算教学中建构算法进行数学抽象的前提是学生已有的计算前经验，包括：①生活经验。教材编排的是幼儿园购迷你南瓜的情境，三年级学生对于迷你南瓜并不熟悉，也没有这样的生活体验，而改用搬牛奶的情境则更贴近学生的生活实际，有利于引发学生的兴趣和思考，进而自主地探索算法。②知识经验。本节课是在学生已经掌握了两位数乘一位数和两位数乘整十数的口算基础上进行教学的，学生只有掌握了这样的知识经验才能理解算理、抽象算法。③方法经验。本节课借助数量关系进行算法理解：第一种方法，先算一次运2 箱牛奶的盒数（14×2=28），再算一共运6 次牛奶的盒数（28×6=168），其本质就是运用乘法结合律；第二种方法，先算10 箱牛奶的盒数（14×10=140），再算2箱牛奶的盒数（14×2=28），最后算12 箱牛奶的盒数（140+28=168），其本质就是运用乘法分配律。

2.组织高效探究活动，展开数学抽象

在教学中组织高效探究活动，是帮助学生在理解算理的基础上展开数学抽象，进而自主构建算法的重要保障和必经之路。在学生根据情境图列出算式“14×12”后，笔者引导学生进一步探索：仔细观察情境图，先独立想一想准备怎样算，再将自己的算法在小组里交流；然后引导学生应用分步计算、画“圆圈图”和竖式计算的方法进行计算；最后组织全班交流展示、比较反思，从而实现借助情境或图示的直观计算向用竖式计算的抽象计算过渡，搭建两位数乘两位数的笔算模型。具体的算法抽象和建构过程可以按照以下步骤展开：①准备算法。在学生列出“14×12”算式后，教师提问学生准备怎样算，提示学生根据图中信息能求出什么问题（如根据先运来10 箱，又运来2 箱，每箱14 盒，能解决什么问题？再如根据每次运2箱，一共运6次，能知道什么？……）。②探究算法。要给予学生足够的时间和空间去独立思考，小组合作探索分步计算的方法（14×10=140，14×2=28，140+28=168）、画“圆圈图”的方法（图略）、竖式计算的方法。在这一过程中，要关注每一位学生是否积极参与探究活动，要对学生进行适时的鼓励和评价，重点帮助在探究过程中感到困难的学生。③交流算法。首先，在交流过程中要引导、鼓励学生充分完整地表述自己的思考过程，呈现自己的思维：计算“14×12”时每一步算的是什么，你能向大家解释一下吗？你能完整地说一说在计算“14×12”时要先算什么、再算什么、最后算什么吗？……其次，在学生表达交流自己的想法和算法的过程中，要培养学生认真倾听的习惯，如提问：“大家听明白他是怎样算的吗？谁再来说一说？大家还有不同意见吗？……”学生在倾听过程中进行思维碰撞和方法交流，有利于学生不断理解并修正算法。④优化算法。在学生已经掌握了分步、画“圆圈图”、用竖式计算“14×12”的方法后，可引导他们比较：虽然方法不一样，但道理是一样的，都是运用“先分后合”。从而抽象概括出竖式计算的方法更加方便简洁，也就优化了算法。

三、基于数学运算，改进练习设计，实现技能形成

毋庸置疑，数学运算是数学核心素养的重要组成部分。数学课程标准强调要加强数的运算地位，同时在“关于课程内容”部分明确指出“应当注重发展学生的运算能力”。因此，在计算教学中，基于数学运算素养的培养，在学生充分理解算理、掌握计算方法后，教师要精心设计有层次的练习，促进学生计算技能的形成，让学生实现从依赖方法和法则的运算转化为一种潜意识的自动化运算。为此，笔者设计了三个层次的练习：既有训练学生单一技能的练习题，也有训练学生复合技能的练习题，还有解决实际问题的练习题。这样设计分层练习，有利于学生理解算理与算法、巩固解决问题的方法，从而实现学生数学运算素养的提升和技能的形成。

1.设计训练单一技能的练习题，进一步理解算法与算理

“想想做做”第（1）题，要求先说出每一步算什么再进行计算；“想想做做”第（2）题，要求根据竖式内容进行填空。题目如下：

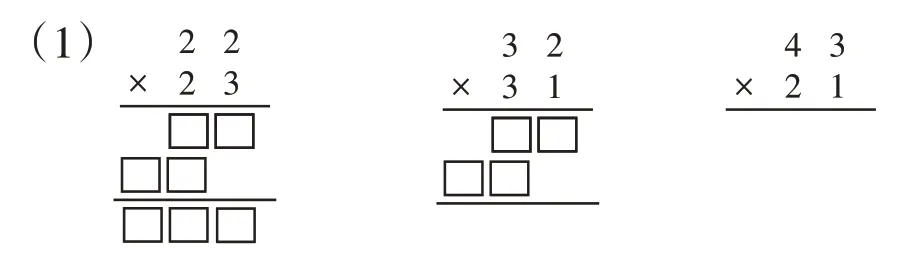
（2）学校买21 个热水瓶，每个23 元。根据下面的竖式，在（ ）里填合适的数。

其中第（1）题是针对两位数乘两位数的笔算过程中每一步先算什么、再算什么、最后算什么的计算程序的专项练习；第（2）题是进一步深化两位数乘两位数的笔算算理的专项练习。这样设计有利于学生在学习例题的基础上，进一步理解两位数乘两位数的笔算方法和算理。

2.设计训练复合技能的练习题，有利于养成综合的运算技能

“想想做做”第（3）题，要求用竖式计算并验算；“想想做做”第（4）题是改错练习。题目如下：

（3）用竖式计算并验算：44×22；11×36；12×23；33×12。

（4）改错练习：

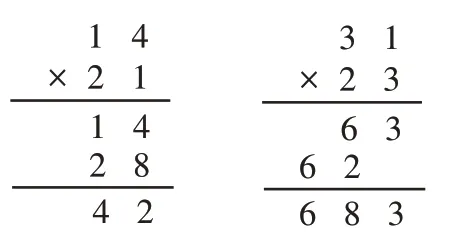
第（3）题要求学生直接根据横式列竖式计算并验算，是把两位数乘两位数的笔算的三个步骤（单一技能）加以组合，形成复合技能，达到正确熟练计算的程度；第（4）题既要学生找出每道题的错误点并加以改正，又要学生说明两位数乘两位数的笔算注意点，加强对学生细心计算习惯的培养。这些是复合技能形成的专项训练，有利于学生进一步巩固和应用两位数乘两位数的算法与算理，从而掌握综合的运算技能。

3.设计解决实际问题的练习题，有利于体会数学价值

“想想做做”第（6）题，要求解决两位数乘两位数的实际问题，题目如下：

（6）李大爷在蔬菜大棚里种了13 垄卷心菜，每垄32棵。一共种了多少棵卷心菜？

第（6）题是引导学生应用两位数乘两位数的笔算解决现实生活中的数学问题，增强学生利用所学知识解决实际问题的能力，是一种综合性的练习，有利于学生体会数学学习的价值，提升学生的数学综合素养。

综上所述，在计算教学中，教师要基于核心素养，从培养学生的逻辑推理、数学抽象和数学运算出发，努力改进与优化教学活动，引导学生在充分理解算理的基础上掌握算法；在解决问题的过程中，教师要引导学生灵活选择算法，能对所采用的算法的合理性进行分析判断；在计算过程中，要求学生能通过有效的训练达到一定的运算速度，不断形成熟练的计算技能，最终提升自己的计算能力与运算素养。