基于滑模自抗扰的PMLSM 电流偏差解耦控制

赵希梅，吴 岑

（沈阳工业大学 电气工程学院，辽宁 沈阳 110870）

1 引 言

近年来，随着日益增长的高速、高精度加工需求，直线电机以其直接驱动的结构和良好的动态性能备受关注［1-2］。永磁直线同步电动机（Permanent Magnet Linear Synchronous Motor，PMLSM）不依靠中间传动环节，采用直接驱动方式，并且散热快，在激光加工领域得到了广泛应用［3-5］。但当电感参数发生变化时，其电流解耦不完全，系统鲁棒性不佳。为提高系统鲁棒性，必须克服PMLSM 电流耦合以及在运行过程中受到的参数变化的影响。

为消除电机运行过程中参数变化，d、q轴电流间存在的耦合等对系统性能造成的不利影响，学者们采用了各种先进的控制方法。文献［6］采用内模控制结合自抗扰控制的方法解决了参数敏感问题并抑制外部负载扰动，但在高速运行时会出现振荡现象。文献［7］针对d、q轴电流耦合问题，采用电压前馈解耦的方法通过反馈的d、q轴电流和速度，对两轴电压进行补偿，并对两轴电流进行解耦，但解耦效果不明显。文献［8］针对d、q轴电流耦合问题，采用电流偏差解耦控制（Current Deviation Decoupling Control，CDDC）的方法进行解耦，但电感参数发生变化时，没有对该扰动进行相应的补偿或抑制，并不能完全实现解耦。文献［9］利用复矢量电流控制器对d、q轴进行电流解耦，动态性能得到一定改善，但是对外部扰动的鲁棒性较差。文献［10］利用电流差值补偿的思想，将定子电流作为状态变量，设计了电流滑模观测器得到定子电流估计量，改善了电感参数变化时系统的鲁棒性，但控制算法过于复杂。滑模自抗扰控制（Sliding Mode Active Disturbance Rejection Control，SADRC）算 法 能降低系统对参数变化的敏感性，对参数变化所引起的扰动进行观测并对系统进行补偿，系统体现出很强的鲁棒性［11］。

为此，本文设计一种基于滑模自抗扰的电流偏差解耦控制（Current Deviation Decoupling Control Based on Sliding Mode Active Disturbance Rejection，SADRC-CDDC）方法来对系统在参数变化时进行电流的解耦，从而提高系统鲁棒性。首先，为了解决两轴电流的耦合问题，分别将两轴电流的给定与反馈量进行作差比较，经过PI 控制器，从作差处引入两轴耦合控制项，得到含耦合项的控制方程且计算得到耦合量，与其叠加以补偿由电流耦合所引起的偏差，设计了CDDC。然后，对CDDC 的耦合项进行分析，得出由于两轴电感标称值与实际不一致，CDDC 不能实现解耦。为实现解耦，建立含有参数变化的d、q轴电流动态方程，选取积分滑模面以及指数趋近律对SADRC 进行设计，用于观测该扰动，且对系统进行补偿，进而实现近似完全解耦。从理论上分析证明了SADRC-CDDC 能保证系统稳定，提高了系统的鲁棒性。通过系统实验，证明了SADRC-CDDC 方案在电流近似完全解耦时明显提高了系统的鲁棒性。

2 PMLSM 数学模型

在d、q旋转坐标系下PMLSM 的电压方程为

其 中：ud、uq，id、iq和Ld、Lq分 别 为d-q轴 的 电 压，电流和电感；Rs为定子电阻；ψf为永磁体磁链；v为动子速度。考虑参数变化的影响，上式可改为：

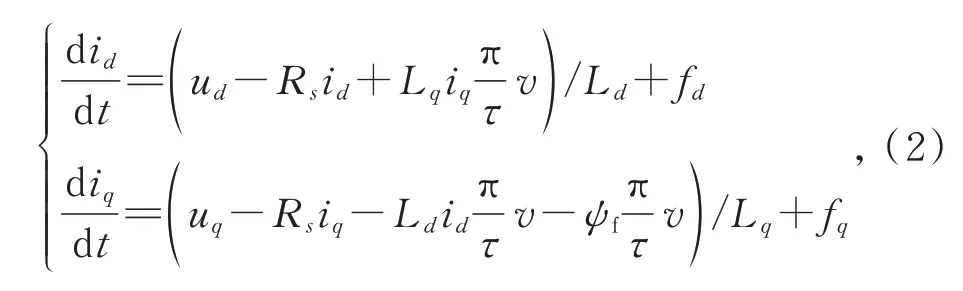
其中：fd、fq分别为d、q轴参数变化的扰动项，定义如下：

其 中：ΔRs=Rs-Rs0；ΔLd=Ld-Ld0；ΔLq=Lq-Lq0；Δψf=ψf-ψf0；Rs0为定子电阻；Ld0、Lq0分别为d、q轴电感参数的标称值。 假设|ΔRs|＜a，|ΔLd|＜b，|ΔLq|＜c和|Δψf|＜d；其中：a，b，c和d为参数变化值的上界。

电磁推力方程为：

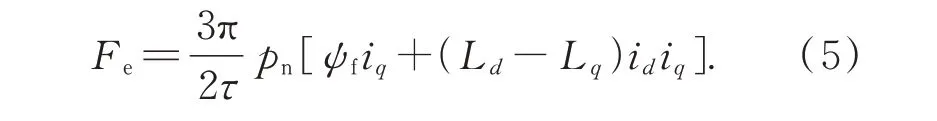
运动方程为：

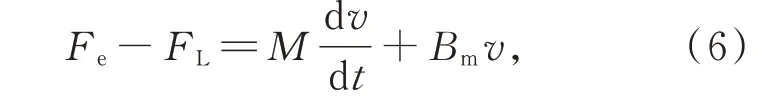
其中，Fe，FL分别为电磁推力和负载扰动；pn为极对数；M为动子质量；Bm为粘滞摩擦系数。

3 PMLSM 控制系统的设计

3.1 PMLSM 系统组成

PMLSM 控制系统结构框图如图1 所示。图中，v*为速度参考输入。速度控制器的输入为v*与v的差，控制器采用的是PI 控制器。采用SADRC-CDDC 方法用于电流控制器，经电流检测以及坐标变换，将d、q轴实际电流与参考电流的差值分别送入SADRC-CDDC。

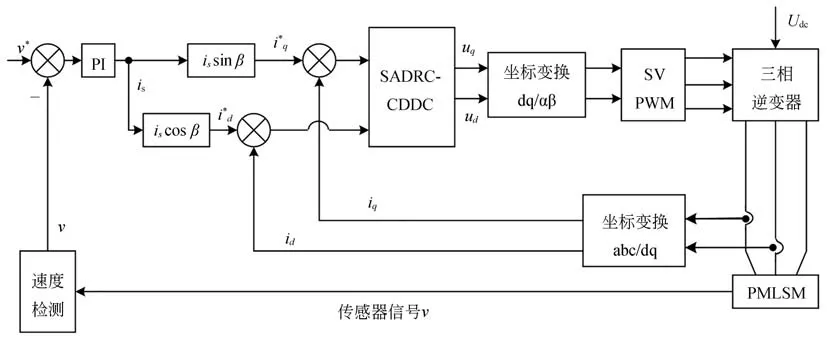
图1 PMLSM 伺服系统框图Fig.1 Block diagram of PMLSM servo system

3.2 CDDC 的设计

PMLSM 在正常运行时，电感电流会很大，当其接近饱和，电感值会发生变化；同时，电感值会在运行过程中随温度变化而变化。此时，电感实际值与给定值产生偏差，使d-q轴电流存在严重耦合。为增强系统在参数变化时的鲁棒性，采用CDDC 对d-q轴电流进行解耦。CDDC 框图如图2 所示。

图2 中，G1（s）、G2（s）分别为控制两轴电流的PI 控制器，G3（s）、G4（s）分别为偏差解耦控制器。分别将两轴电流的给定与反馈量进行作差比较，经过G1（s）、G2（s），生成各自的给定电压，再从做差处引入G3（s）、G4（s），与给定电压加以补偿由电流耦合引起的偏差。得到控制方程为：

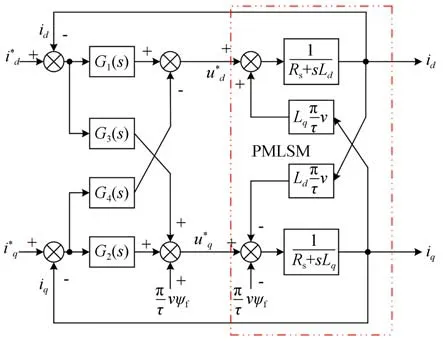
图2 电流偏差解耦控制框图Fig.2 Block diagram of current deviation decoupling control

将式（7）进行变换并由克拉姆法则得出两轴耦合方程为：

要想实现解耦，要满足条件Adq/Δ=0、Aqd/Δ=0，由此解得G4（s）、G3（s）为：

令上式中分子上的Ld、Lq为实际值L^d、L^q，该估计值为电机正常运行时的电感参数。Rs在PMLSM 温度变化时，阻值变化很小，对解耦控制器G2（s）、G3（s）影响可忽略。由式（9）、（10）知，当且仅当L^d=Ld、L^q=Lq时，才能消除两轴间电流耦合。

3.3 SADRC-CDDC 的设计

由于参数变化，电感估计值与实际值在运行过程中会产生偏差造成解耦不完全，CDDC 不能完全补偿解耦量。为降低系统对参数变化的敏感度，采用SADRC 对参数变化所造成的扰动进行观测，并对系统进行补偿，再解耦。基于SADRC-CDDC 的PMLSM 伺服系统框图如图3所示。

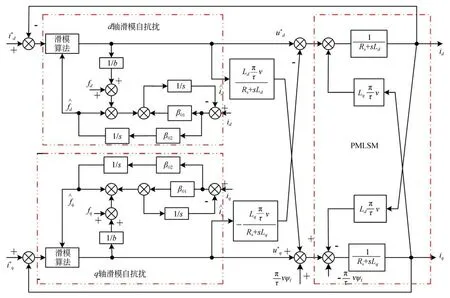
图3 基于SADRC-CDDC 的PMLSM 伺服系统框图Fig.3 Block diagram of PMLSM based on SADRC-CDDC

为估计参数变化在q轴所引起的扰动fq，将ADRC 中的观测器设计为：

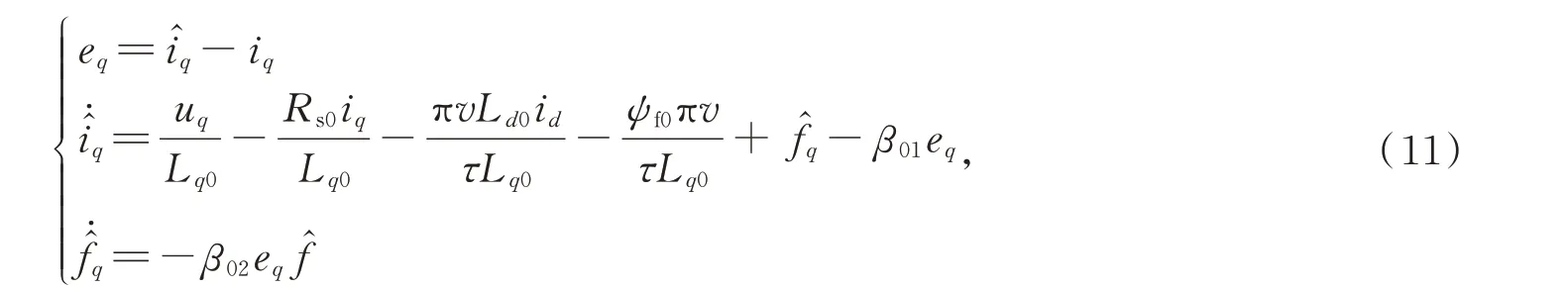
滑模控制算法对扰动具有很强的鲁棒性，因此将滑模控制算法引入ADRC，使系统在其参数变化时鲁棒性得以保证。

定义q轴电流误差esq如下：

由式（14）、（15）和（16）有：

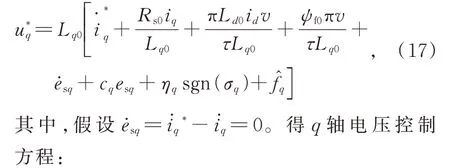
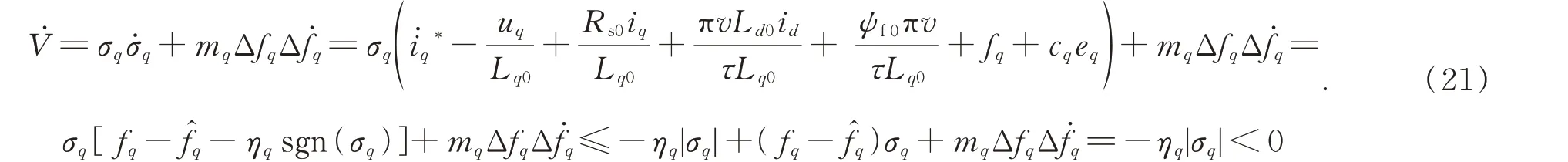
所以V＜0，即证明了q轴电压控制的渐近稳定性。

同理，d轴电压的控制方程为：

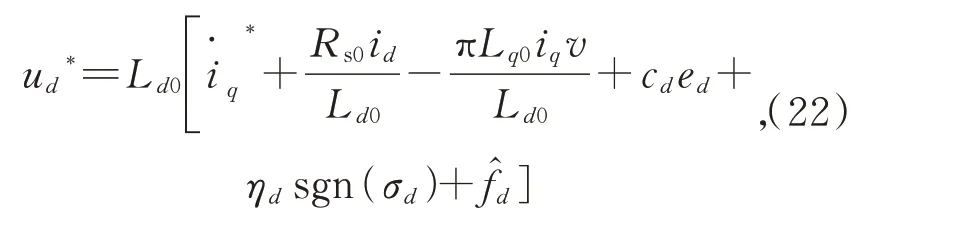
其中：ηd＞0，为d轴扰动估计量。

4 测量实验与结果

将DSP TMS320F28335 作为PMLSM 伺服系统实验的核心控制单元，其控制系统结构如图4 所示。其硬件结构可分为运算控制部分、供电电路单元、检测元件和PMLSM。运算控制单元为PC 和DSP；PMLSM 的供电部分由整流器和逆变器组成，逆变器开关频率为5 kHz。测试平台如图5 所示。选择PMLSM 参数为：Ld=0.016 8 H，Lq=0.026 7 H，Rs=2.6 Ω，M=17 kg，Bm=0.2 N·s·m-1，pn=1，ψf=0.24 Wb，电机额定带载为200 N。为使系统性能最佳，对参数进行反复调试。 PI 参数为Kp=20.6，Ki=179.33；SADRC 参数为ω0=8.75，cd=0.1，ηd=0.5，cq=0.1，ηq=0.3。

图4 PMLSM 控制系统硬件结构图Fig.4 Hardware structure diagram of PMLSM control system

图5 测试平台Fig.5 Test platform

图6 为空载启动的速度响应曲线。由图看出，电机在启动阶段，有超调，在0.1 s 达到稳态。电机在0.5 s 突加100 N 负载后，速度减小，经0.04 s 后恢复至给定速度。电机在1 s 时将负载突减至50 N 后，速度增大，经0.01 s 后恢复至给定速度。由此可知，该系统能满足调速系统要求。

图6 空载启动的速度响应曲线Fig.6 Speed response curve of no-load start

图7（a）和7（b）分 别 为 当Ld=L^d，Lq=L^q时空载启动在0.5 s 突加100 N 负载和在1s 时将负载突减至50 N，采用CDDC 方法和SADRCCDDC 方法的d、q轴电流的响应曲线。空载时，d轴电流最大振荡幅度分别为0.37 A 和0.34 A，采用SADRC-CDDC 方法减小了约8.11%，q轴电流最大振荡幅度分别为0.15 A 和0.13 A，采用SADRC-CDDC 方法减小了约13.33%；在0.5 s 突加100 N 负载后，d轴电流最大振荡幅度分别为0.51 A 和0.32 A，采用SADRC-CDDC方法减小了约37.25%，q轴电流最大振荡幅度分别为0.16 A 和0.15 A，采用SADRC-CDDC方法减小了6.25%；在1 s 时将负载突减至50 N后，d轴电流最大振荡幅度分别为0.32 A 和0.29 A，采用SADRC-CDDC 方法减小了约9.38%，q轴电流最大振荡幅度分别为0.49 A 和0.47 A，采用SADRC-CDDC 方法减小了约4.08%。

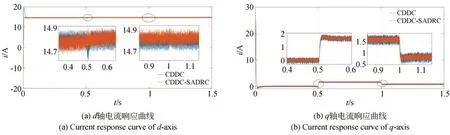
图7 Ld=，Lq= 时的空载启动电流响应曲线Fig.7 Current response curves with Ld=，Lq=of no-load start

图8（a）～8（d）为 当Ld=1.2，Lq=0.8时空载启动在0.5 s 突加100 N 负载和在1 s 时将负载突减至50 N，采用CDDC 方法和SADRCCDDC 方法的d、q轴电流的响应曲线。空载时，d轴电流最大振荡幅度分别为0.44 A 和0.20 A，采用SADRC-CDDC 方法减小了约54.55%，q轴电流最大振荡幅度分别为0.32 A 和0.12 A，采用SADRC-CDDC 方法减小了62.50%；在0.5 s突加100 N 负载后，d轴电流最大振荡幅度分别为0.42 A 和0.19 A，采用SADRC-CDDC 方法减小了约54.76%，q轴电流最大振荡幅度分别为0.25 A 和0.11 A，采用SADRC-CDDC 方法减小了56.00%；在1 s 时将负载突减至50 N 后，d轴电流最大振荡幅度分别为0.43 A 和0.28 A，采用SADRC-CDDC 方法减小了约34.88%，q轴电流最大振荡幅度分别为0.42 A 和0.12 A，采用SADRC-CDDC 方法减小了约71.43%。当Ld=1.3，Lq=1.5时 空 载 启 动，在0.5 s 突 加100 N 负载和在1 s 时将负载突减至50 N 时采用采用SADRC-CDDC 方法的电流振荡幅度明显减小，鲁棒性增强。

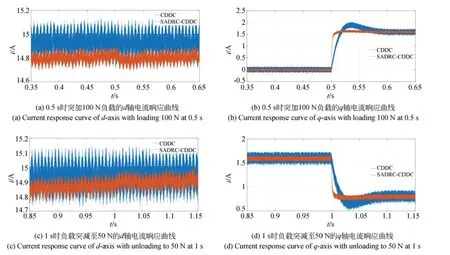
图8 Ld=1.2，Lq=0.8时的空载启动d 轴和q 轴电流响应曲线Fig.8 Current response curves of d and q axis with Ld=1.2，Lq=0.8of no-load start

图9（a）～（d）为当Ld=1.3，Lq=1.5时空载启动，在0.5 s 时突加100 N 负载和在1 s 时将负载突减至50 N 时采用CDDC 方法和SADRC-CDDC 方法的d、q轴电流的响应曲线。空载时，d轴电流最大振荡幅度分别为0.45 A 和0.21 A，采用SADRC-CDDC 方法减小了约53.33%，q轴电流最大振荡幅度为0.31 A 和0.12 A，采用SADRC-CDDC 方法减小了约61.29%；在0.5 s 突 加100 N 负 载 后，d轴 电 流 最大振荡幅度分别为0.45 A 和0.19 A，采用SADRC-CDDC 方法减小了约57.78%，q轴电流最大振荡幅度分别为0.25 A 和0.11 A，采用SADRC-CDDC 方法减小了56.00%；在1 s 时将负载突减至50 N 后，d轴电流最大振荡幅度分别为0.43 A 和0.21 A，采用SADRC-CDDC 方法减小了约51.16%，q轴电流大振荡幅度分别为0.23 A 和0.12 A，采用SADRC-CDDC 方法减小了约47.83%。 当Ld=1.2，Lq=0.8时 空 载 启动，在0.5 s 突加100 N 负载和在1 s 时将负载突减至50 N 时采用SADRC-CDDC 方法的电流振荡幅度明显减小，鲁棒性增强。

图9 Ld=1.3，Lq=1.5 时的空载启动d 轴和q 轴电流响应曲线Fig.9 Current response curves of d and q axis with Ld=1.3，Lq=1.5of no-load start

图10 为额定负载下启动的速度响应曲线。由图看出，电机在启动阶段，有超调，在0.09 s 达到稳态。电机在0.5 s 突减100 N 负载后，速度增大，经0.04 s 后恢复至给定速度。由此可知，该系统能满足调速系统要求。

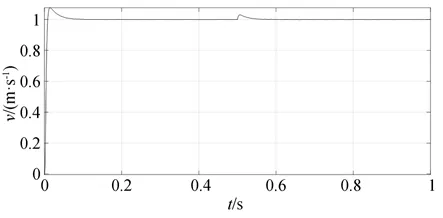
图10 额定负载启动的速度响应曲线Fig.10 Speed response curve of rated load start

图11（a）和（b）分别为当Ld=，Lq=时额定负载下启动，在0.5 s 突减100 N 负载时采用CDDC 方法和SADRC-CDDC 方法的d、q轴电流的响应曲线。200 N 额定负载时，d轴电流最大振荡幅度分别为0.21 A 和0.19 A，采用SADRC-CDDC 方法减小了约9.52%，q轴电流最大振荡幅度为0.31 A 和0.29 A，采用SADRC-CDDC 方法减小了约6.45%；在0.5 s 突减100 N 负载后，d轴电流最大振荡幅度分别为0.22 A 和0.20 A，采用SADRC-CDDC 方法减小了约9.09%，q轴电流最大振荡幅度分别为0.32 A 和0.30 A，采 用 SADRC-CDDC 方 法 减 小 了6.25%。

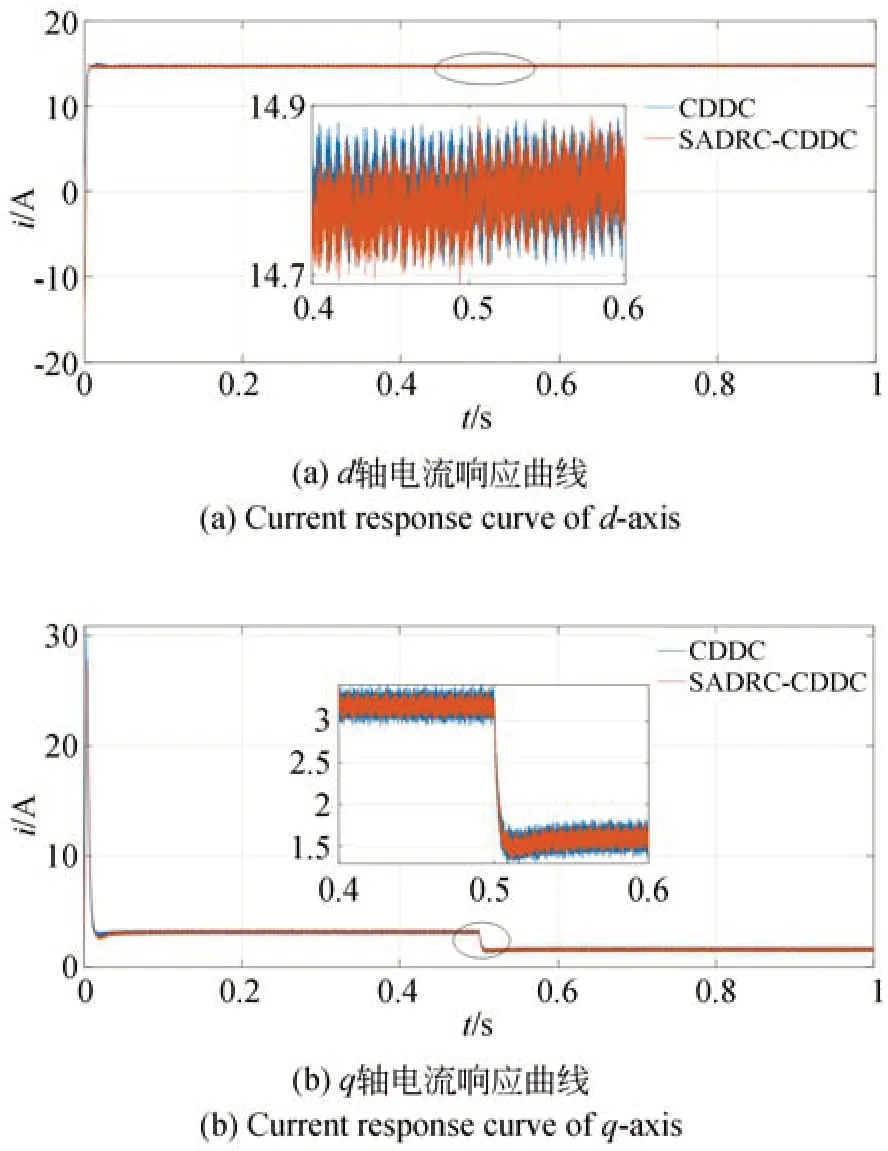
图11 Ld=，Lq=时额定负载启动的d 轴和q 轴电流响应曲线Fig.11 Current response curves of d and q axis withLd=，Lq=of rated load start

图12（a）和（b）分 别 为 当Ld=1.2，Lq=0.8时额定负载下启动，在0.5 s 突减100 N 负载时采用CDDC 方法和SADRC-CDDC 方法的d、q轴电流的响应曲线。额定负载时，d轴电流最大振荡幅度分别为0.44 A 和0.22 A，采用SADRC-CDDC 方法减小了50.00%，q轴电流最大振荡幅度为0.47 A 和0.20 A，采用SADRC-CDDC 方法减小了约57.45%；在0.5 s 突减100 N负载后，d轴电流最大振荡幅度分别为0.43 A 和0.21 A，采用SADRC-CDDC 方法减小了约51.16%，q轴电流最大振荡幅度分别为0.45 A和0.23 A，采用SADRC-CDDC 方法减小了约48.89%。当Ld=1.2，Lq=0.8时额定负载下启动，在0.5 s 突减100 N 负载时采用SADRCCDDC 方法的电流振荡幅度明显减小，鲁棒性增强。

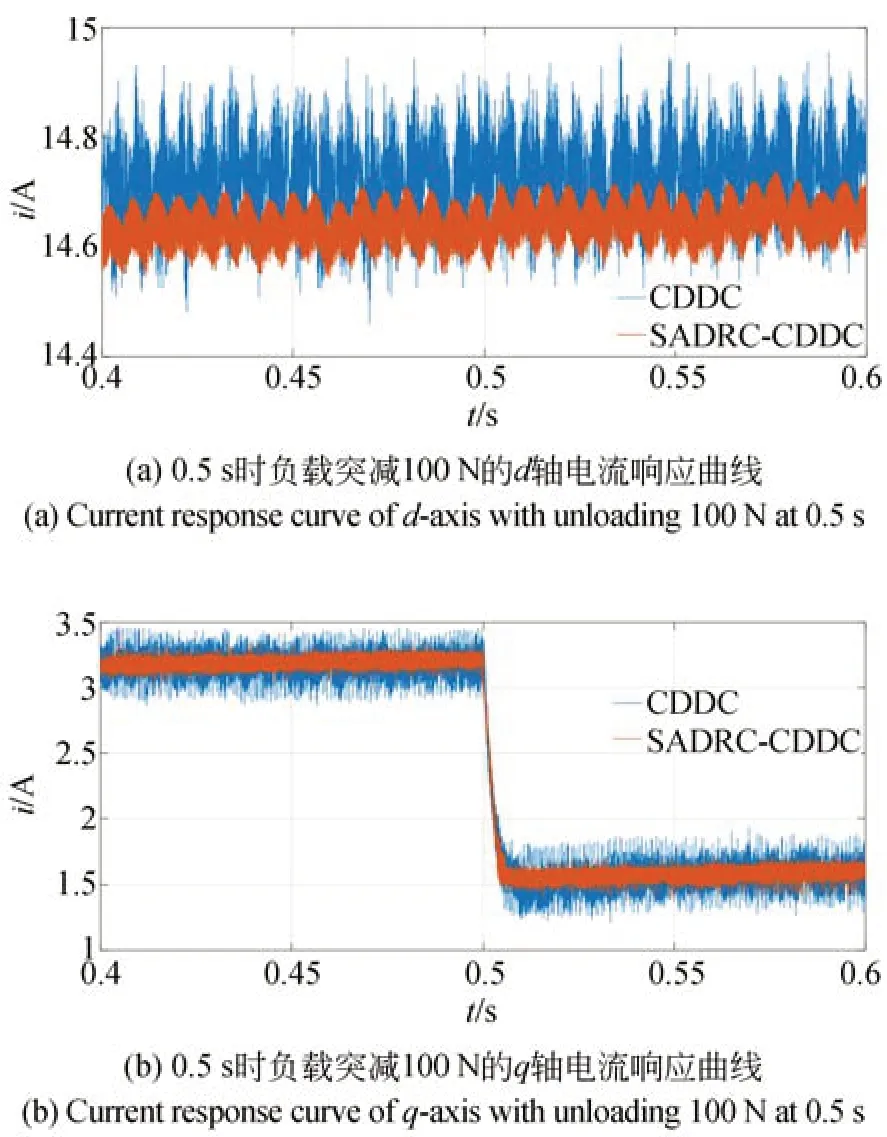
图12 Ld=1.2，Lq=0.8 时 额 定 负 载 启 动 的d 轴 和q 轴电流响应曲线Fig.12 Current response curves of d and q axis with Ld=1.2，Lq=0.8of rated load start

图13（a）和（b）分 别 为 当Ld=1.3，Lq=1.5时额定负载下启动，在0.5 s 突减100 N 负载时采用CDDC 方法和SADRC-CDDC 方法的d-q轴电流的响应曲线。额定负载时，d轴电流最大振荡幅度分别为0.42 A 和0.19 A，采用SADRC-CDDC 方法减小了约54.76%，q轴电流最大振荡幅度为0.49 A 和0.20 A，采用SADRCCDDC 方法减小了约59.18%；在0.5 s 突减100 N 负载后，d轴电流最大振荡幅度分别为0.44 A和0.21 A，采用SADRC-CDDC 方法减小了约52.27%，q轴电流最大振荡幅度分别为0.45 A和0.21 A，采用SADRC-CDDC 方法减小了约53.33%。当Ld=1.3，Lq=1.5时额定负载下启动，在0.5 s 突减100 N 负载时采用SADRCCDDC 方法的电流振荡幅度明显减小，鲁棒性增强。

图13 Ld=1.3，Lq=1.5 时 额 定 负 载 启 动 的d 轴 和q 轴电流响应曲线Fig.13 Current response curves of d and q axis with Ld=1.3，Lq=1.5 of rated load start

通过以上分析，无论是空载启动实验还是额定负载启动实验，电感实际值与标称值相等时（即Ld=，Lq=时）采用CDDC 和SADRCCDDC 方法的电流振荡幅度无明显差别；而电感实际值与标称值不相等时（即Ld=1.2，Lq=0.8和Ld=1.3，Lq=1.5时），采用SADRCCDDC 方法的电流振荡幅度相对于CDDC 方法明显减小，降低了参数变化的敏感性，在电感参数变化时实现近似完全解耦，系统表现出很强的鲁棒性，而CDDC 方法对电机参数具有很强的依赖性。

5 结 论

针对PMLSM 伺服系统易受电感参数变化影响，且d、q轴电流存在耦合，降低了系统的鲁棒性问题。为了对两轴电流进行解耦，设计了SADRC-CDDC。若只采用CDDC 方法构造耦合多项式，分析得到电感参数变化时不能实现解耦。利用SADRC 对参数造成的扰动进行观测，再对系统进行补偿，在克服参数变化扰动的同时实现对电流的近似完全解耦。通过理论和实验分析得出，SADRC-CDDC 方法与CDDC 方法比较，在电机运行过程中，系统对参数变化的敏感度降低，由于耦合而造成的d、q轴电流振荡幅度明显减少，参数变化情况下d轴电流最大振荡幅度减少了34.88%～54.76%，q轴电流最大振荡幅度减少了47.83%～71.43%，系统鲁棒性增强，实现了系统的近似完全解耦。