基于二维随机场的地基大型光学望远镜风扰动时程模拟与性能预测
2022-03-11曹玉岩王建立王志臣李洪文初宏亮李玉霞
曹玉岩,王建立,王志臣,李洪文,张 岩,初宏亮,李玉霞
(1. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2. 中国科学院大学,北京 100049)
1 引 言
地基望远镜是连接人类与未知宇宙的桥梁,帮助人们观测、探索宇宙奥秘。随着对宇宙暗弱目标研究的深入,对如深空恒星的形成与演变、星系分布与结构及演变物理过程对人类的影响、暗物质与暗能量的本质等等的探索,要求未来的望远镜不但要看的清、还要看得远,这推动了地基望远镜朝大口径、高分辨力方向发展[1]。
随着地基望远镜口径不断增大,风扰动成为影响望远镜成像质量最为关键的因素之一。首先,望远镜台址通常选在高海拔偏僻地区来避免杂光污染并提高大气视宁度,这些地区通常风速都很大(如夏威夷莫纳克亚山天文台风速高达20 m/s)。其次,望远镜结构刚度随口径的增大而下降,系统谐振频率随之降低。此外,风扰动功率谱中包含有较大的低频能量(0.1~1 Hz),在望远镜基频处风压能量集中,容易引起望远镜系统的共振,而且风载具有随机和时变特性[2]。一些望远镜往往因为风大而难以获取有效科学数据,甚至不得不放弃观测。风扰动的分析与抑制已成为地基望远镜领域的热点和难点,受到了越来越多的科学家们的关注[3-10]。
尽管光学望远镜外部一般有圆顶防护,能够显著降低其内部风速,但为了满足圆顶内视宁度的要求,内部要适当通风,而且光学望远镜波长较短,圆顶内的残余风仍然会对望远镜系统性能产生显著影响[3]。针对这一问题,MacMynowski等基于Gemini 望远镜镜面风速和风压测量[5]、风道测试[6]和计算流体动力学仿真CFD[7]得到的数据对望远镜圆顶内部的风扰动特性进行了深入研究,并提出了参数化模型[8,9],该参数化模型可根据望远镜、风速及圆顶等相关参数将风扰动转化为作用在望远镜主、次镜上载荷,给结构设计优化带来极大的方便。在国内,杨德华等[11]针对LAMOST 反射施密特改正镜,研究了其拼接子镜及整体在风扰动作用下的静态和动态响应,采用风速功率谱密度法分析了其对镜面面形和跟踪指向精度的影响;周超等[12]以长春光机所研制的1.23 m 自适应光学望远镜为例,研究了风扰动对主镜面形的影响及望远镜在动态风扰作用下的随机响应;潘年等[13]采用流体动力学仿真方法CFD 研究了国内某2 m 望远镜风扰特性,分析了外界风速10 m/s 情况下望远镜不同俯仰角时流场中截面空气速度、压力、湍流动能以及主镜面静压力的瞬态分布情况,并与Gemini 望远镜实测结果进行了比较。徐江海等[14]采用CFD 分析圆顶形式对内部风湍流的影响。以上研究从不同的角度分析了外界风扰动对望远镜性能产生的影响。
从上述文献中可以看出,望远镜口径不断增大,系统刚度和谐振频率下降,风扰动的影响应在望远镜建造阶段予以重视。风扰动包含稳态分量和非稳态分量两部分,稳态分量(静态风载荷)是恒定的,通过系统主动控制很容易得到抑制,但抑制非稳态分量(动态风扰动)引起的振动则存在一定的困难。针对此问题,已有多位学者采用计算机仿真手段深入分析了非稳态风扰动对望远镜性能的影响程度[8-9]。非稳态风扰动分量具有较强的随机性,目前已有的大部分研究均是从频率角度考虑风扰动的影响,时域角度的研究则很少。然而,对于大型地基望远镜这样复杂结构来说,其结构中往往存在一定的非线性特性,风扰动的时程分析模拟是必不可少的,而且从时域角度分析与工作过程更为接近,这也更利于进行实验比较。
基于上述原因,本文以长春光机所研制的2 m 口径地基光学望远镜为例,从时域角度研究风扰动对望远镜的影响,并进行性能预测。首先,详细介绍了望远镜结构组成,基于有限元方法建立结构动力学模型,并通过模态变换方法将动力学模型转换到模态坐标系下,从而降低了模型维数,提高了计算效率。然后,考虑到大型地基望远镜结构尺度相对较大,将望远镜圆顶内的风速场表达为随时间和空间位置变化的二维随机场,通过引入互相关函数或互功率谱矩阵来刻画随机场的统计特征。基于互功率谱矩阵,采用谱表达方法实现时程模拟。为了克服在离散采样点数提高时,谱表达方法中各个离散采样点处互功率谱矩阵Cholesky 分解出现数值不稳定的问题,引入了文献[15-17]所述波数谱方法,从而可以表达空间和时间频率范围内几乎连续的随机场。最后,对2 m 望远镜进行风速场模拟并在此风速场下进行性能分析。
2 望远镜结构动力学建模
2 m 级地基光学望远镜结构简图如图1 所示,总体高度为6.4 m,宽度为3.7 m,总质量接近30 吨。从望远镜结构角度考虑,主要包括地平式机架、主镜和次镜三部分,其余附属结构对本文所研究内容影响较小,在此不予考虑。
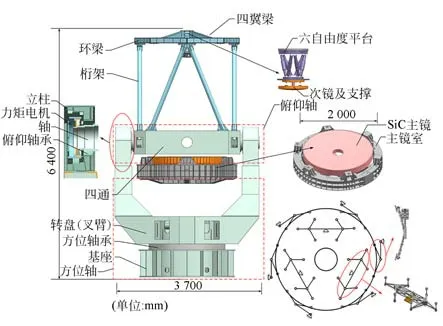
图1 2 m 望远镜结构简图Fig.1 Simplified structure of 2 m telescope
自无穷远目标发出的光束经过主镜和次镜反射后,被像面位置处的高灵敏度探测器接收,实现光信号到电信号的转换,从而获得清晰的目标图像。地平式机架是主、次镜及其他附件的载体,通过俯仰轴和方位轴的高精度回转运动实现望远镜对任意天区的精确指向和对目标的稳定跟踪测量。
望远镜主镜材料为SiC,具有比刚度大、质量轻、热稳定性好等优点,采用A-Frame 型柔性侧支撑方式,并结合18 点机械式whiffletree 轴向支撑方式,支撑结构原理如图1 所示。同样,次镜采用具有热变形匹配的bipod 型结构来消除热膨胀系数差异性对次镜面形精度的影响。此外,次镜结构整体通过Hexapod 并联机构实现位置调整与补偿。
针对上述2 m 望远镜简化结构,采用有限元方法建立望远镜结构动力学模型如图2 所示。在全局坐标系下,望远镜结构动力学模型可以表达为二阶微分方程,即:
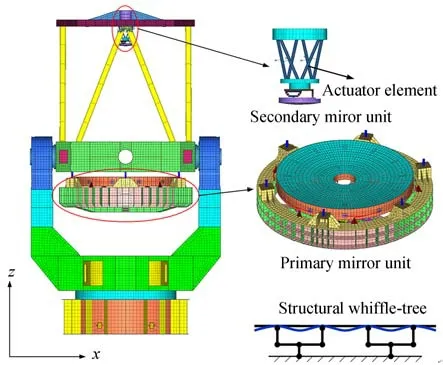
图2 2 m 望远镜结构有限元模型Fig.2 Finite element model of 2 m telescope structure
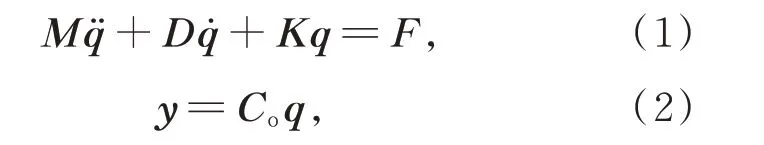
其中:M,D,K分别为质量矩阵,阻尼矩阵和刚度矩阵;F为载荷向量;y为输出位移向量;q¨,q˙,q分别为节点加速度,速度和位移向量;Co为输出矩阵,在风扰动分析中,主要关注的是主、次镜节点的位移,因此输出矩阵为与主、次镜节点位置相关的矩阵。
由于望远镜结构非常大,有限元模型节点数量非常多,上述以节点变量来表达的结构动力学模型将非常大。为了提高计算效率,降低后续风扰动模拟的计算难度,对结构动力学模型进行模态变换,即

其中,Φ为振型矩阵,其表达式为:
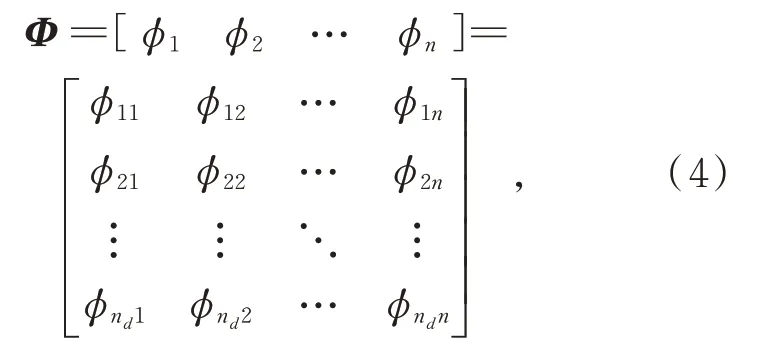
其中:φij表示第i个节点自由度上的第j阶振型;nd为模型阶数,即节点的全部自由度总和;n为提取的模态阶数。
将式(3)带入式(1)和式(2),并在式(1)左乘ΦT得:
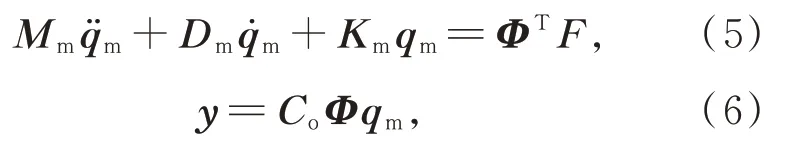
其中:Mm=ΦTMΦ,Dm=ΦTDΦ,Km=ΦTKΦ。
对以模态变量表达的结构动力学方程(5)和(6)进一步简化可得:
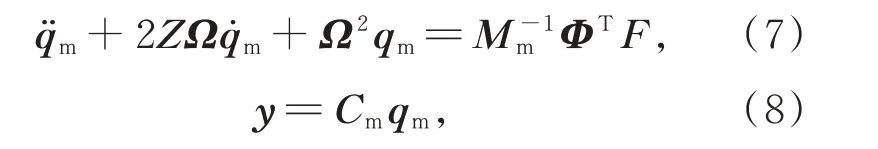
其 中:Z=diag(ζ1,ζ2,…,ζn)为 阻 尼 系 数 矩 阵,Ω=diag(ω1,ω2,…,ωn)为模态频率矩阵,Cm=CoΦ。
为了应用线性系统相关理论,将式(7)和(8)表达的结构动力学模型转化为状态空间表达形式。定义状态变量为:
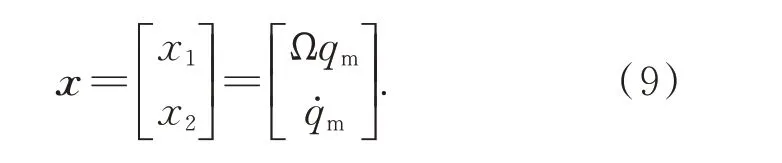
将式(9)带入式(7)和(8)可得:
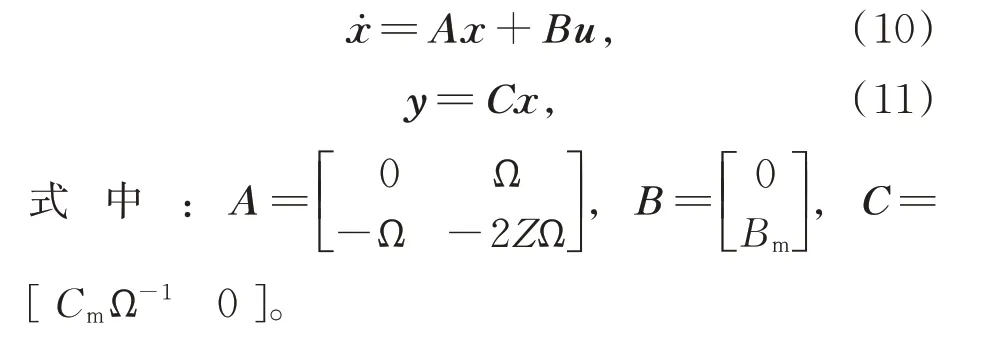
与式(1)和(2)相比,状态空间方程(10)和(11)表达的结构动力学模型的维数大大降低,从而可以显著提高计算效率。
3 随机风扰动建模
对于地基大型光学望远镜而言,风扰动的直接影响是造成望远镜视轴抖动及光学元件(主要是主镜和次镜)的振动和变形,进而导致焦面处图像抖动和模糊。风扰动具有随机性,作用在望远镜结构上产生的变形非常复杂,即使采用计算流体动力学分析方法CFD 也很难准确模拟[7]。为了简化计算模拟过程,本文将风扰动对望远镜的作用简化为如图3 所示的三种方式:(1)载荷作用在次镜及其支撑桁架上,引起次镜抖动;(2)载荷作用在主镜及其支撑结构上引起主镜变形和位置的变化;(3)载荷作用在次镜及支撑桁架上,造成俯仰轴的扰动,进而引起视轴抖动。风扰动的综合作用效果是引起主、次镜光轴相对位置出现偏差,镜面出现面形误差以及视轴抖动,进而造成光学系统性能下降。
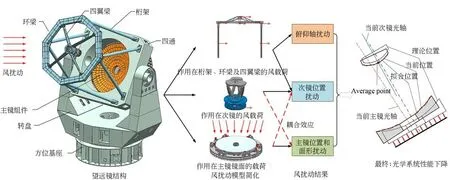
图3 风扰动作用简化模型Fig.3 Simplified model of wind disturbance
3.1 基于二维随机场的风速时程模拟
从图1 已知望远镜的横向和纵向最大跨度相对较大,分别为6.4 m 和3.7 m,对风速进行时程模拟需要同时考虑时间频率和空间频率,且空间频率需要考虑多个维度。这里提出了以平面内的二维随机场来模拟作用在望远镜结构上的风速,风速在空间上任何一点的时间历程上既具有随机性又符合统计规律,其功率谱与预先已知的功率谱密度一致。首先推导一维随机场,然后再将其拓展至二维情况。
定义X(t)为离散且相互独立的随机过程向量,即:
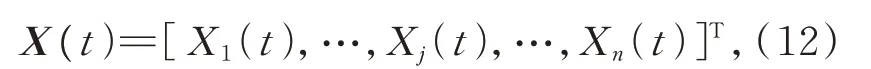
其中,Xj(t)为第j个单变量随机过程。
随机过程向量中的各元素均为相互独立的单变量随机过程,但作为一个整体,不同元素之间存在一定的相关关系,可以用互相关函数矩阵或互功率谱密度矩阵来表示,即:
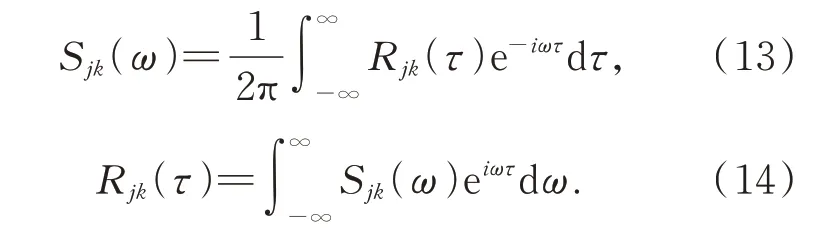
为了从时程角度模拟随机过程,首先需要对其互功率谱密度矩阵进行分解,即:
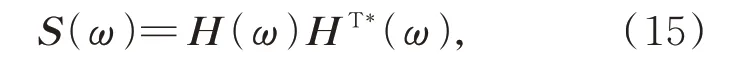
其中:H(ω)为下三角矩阵,T*表示复共轭转置,上述分解可以通过Cholesky 方法实现。
根据式(15),随机过程向量X(t)的时间历程可以表达为:

尽管式(16)给出了随机过程向量的时间历程显式表达式,但当采样点数N→∞时,功率谱密度矩阵接近奇异,无法应用Cholesky 方法对其进行分解。为了解决该问题,本文引入波数谱,建立在空间和时间上几乎连续的风速模型,这可以在规定空间范围内得到无穷采样点的风速,从而避免了互功率谱矩阵的Cholesky 分解。波数谱的表达式可以由自功率谱和相干函数积分得到,即:
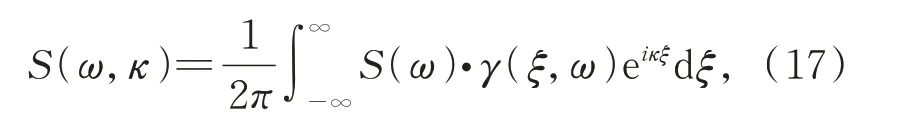
其 中,S(ω)为 自 谱,ξ为 空 间 距 离,κ为 波 数,γ(ξ,ω)为相干函数,通常选择Davenport 相干函数模型。
基于波数谱(17),可以得到随机过程向量X(t)的时间历程表达式为:

式(18)仅给出了考虑一维空间频率和时间频率的表达式。然而,对于望远镜来说,尤其是对于大口径主镜来说,风速模拟时考虑平面内二维空间频率更合理。为此,需要将式(18)拓展至二维空间频率范围。

二维空间的波数谱可以由式(19)积分得到,即:

通常描述风扰动的功率谱选择Davenport 功率谱,其表达式为:
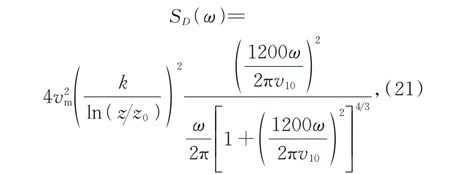
其中:vm为平均风速,k为风阻系数。
根据二维空间的波数谱表达式(20),可得二维空间随机场的时程表达式为:
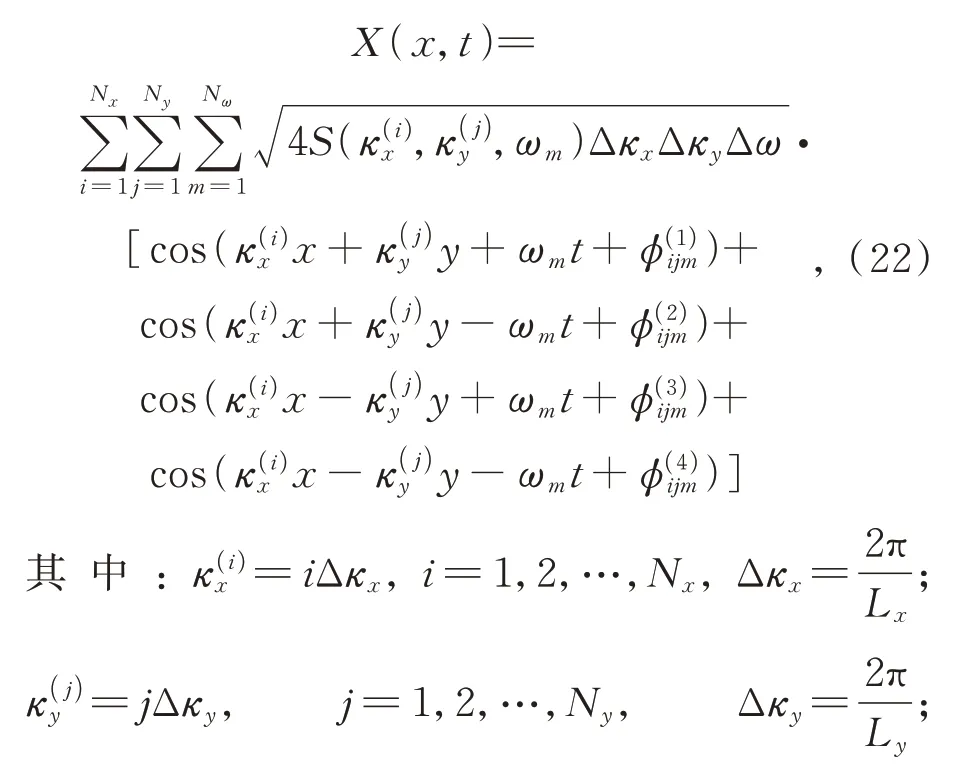

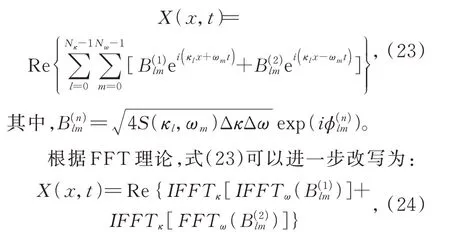
3.2 FFT 算法
式(18)和式(22)分别给出了一维空间和二维空间情况下的风速时程表达式,具有相同的表达形式,分别为二重和三重求和表达式。随着采样点数量的增大,计算效率将会显著下降。为了改善计算效率,这里引入快速傅里叶算法FFT。
为了利用FFT,将式(18)改写为:
其 中,FFT(·)和IFFT(·)分 别 表 示 快 速 傅 里 叶 变换和逆变换。
同样,式(22)可以变换为:

对比式(26)和(22)可以发现,通过引入FFT算法,空间频率和时间频率的多重求和被FFT算法代替,从而显著改善了风速模拟的计算效率。
3.3 风载荷计算方法
从前面推导已知风速具有随机变化的特征,风速的幅值v可以表达为常量或平均风速vm和大气湍流引起的时变量Δv之和,即:

风载荷的表达式为:
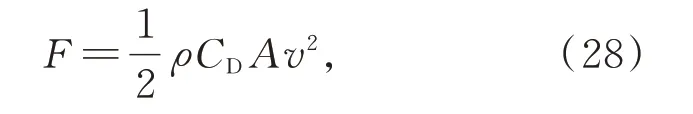
其 中:ρ为 空 气 密 度,CD为 风 阻 系 数,A为 迎 风面积。
同样,风载荷也可以分解为稳态量和非稳态量的和,即:
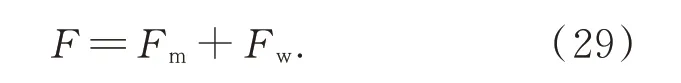
非稳态风载荷Fw与Δv有关,通过对(28)Taylor 展开可得:

望远镜结构非常复杂,作用在望远镜上的风载荷也同样非常复杂。从望远镜结构的角度,主要考虑图3 所示的三方面作用,即主镜、桁架以及环梁和次镜上的风扰动作用。为了简化分析计算难度,将望远镜划分为三层,如图4 所示,以这三层的位置来离散采样点,然后根据式(30)来计算风载荷,并根据结构状态方程(10)和(11)来计算风扰动响应。
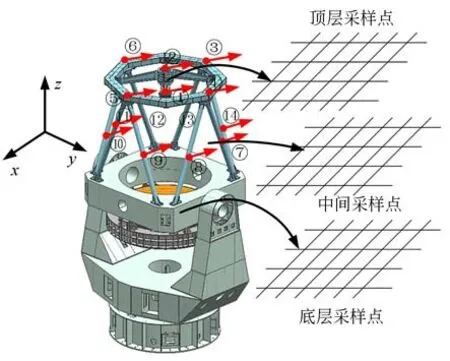
图4 望远镜上的风载荷Fig.4 Wind load acting on telescopes
4 数值算例
以图1 所示的2 m 口径地基望远镜为例,采用本文提出的基于二维随机场的风扰动建模方法模拟望远镜的风扰动环境,并与已有文献进行对比,其中与望远镜结构相关的参数如表1 所示。此外,对随机风扰动对望远镜的影响进行了详细的仿真分析并对光学性能进行预测。
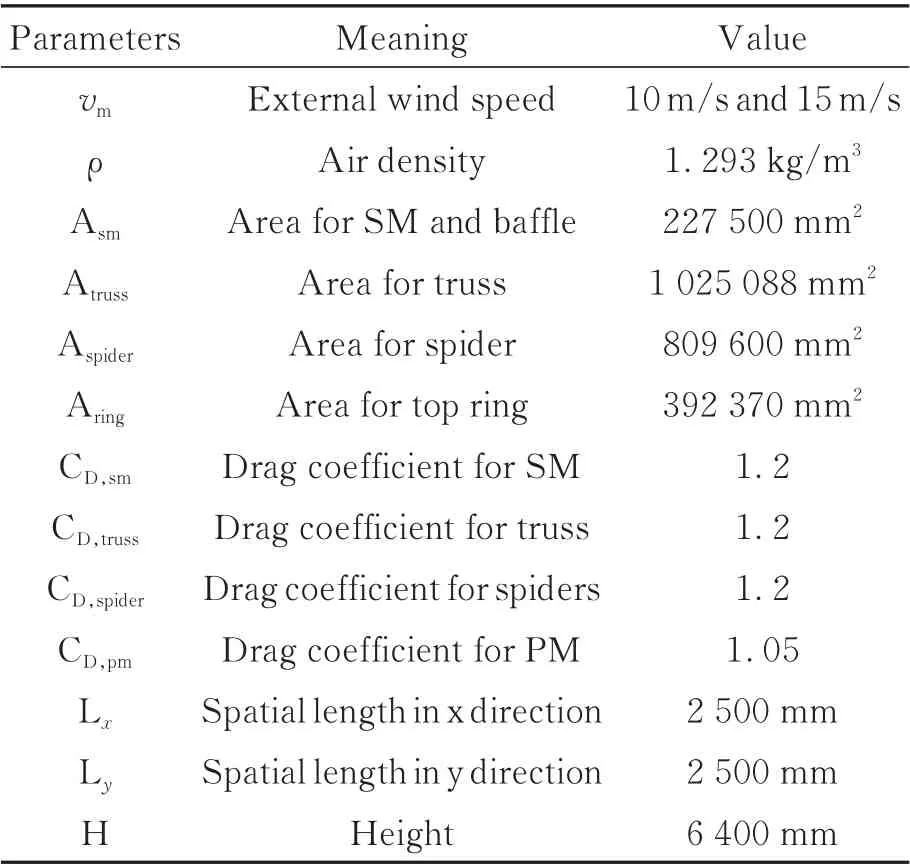
表1 风载荷计算参数Tab.1 Parameters of wind load
4.1 随机风扰动的模拟与验证
根据3.2 节所述二维随机场的理论,按图4所示将作用在望远镜的随机风速场简化为三层离散网格并在这些网格点生成随机风速数据,随机风速场离散参数如表2 所示。以主镜为例,在主镜镜面位置按图5 所示随机采样6 个位置,外界平均风速10 m/s 情况下,风速的时程变化过程以及相应的功率谱如图6 所示。
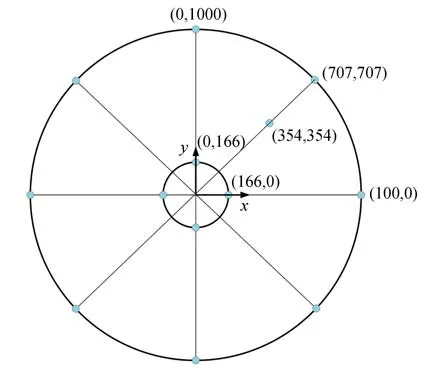
图5 主镜采样位置Fig.5 Sampling points of the primary mirror

表2 风速场离散参数Tab.2 Discretized parameters of wind speed fields
从图6 所示的主镜上6 个采样点位置的风速时程变化曲线以及功率谱曲线可以得出以下结论:
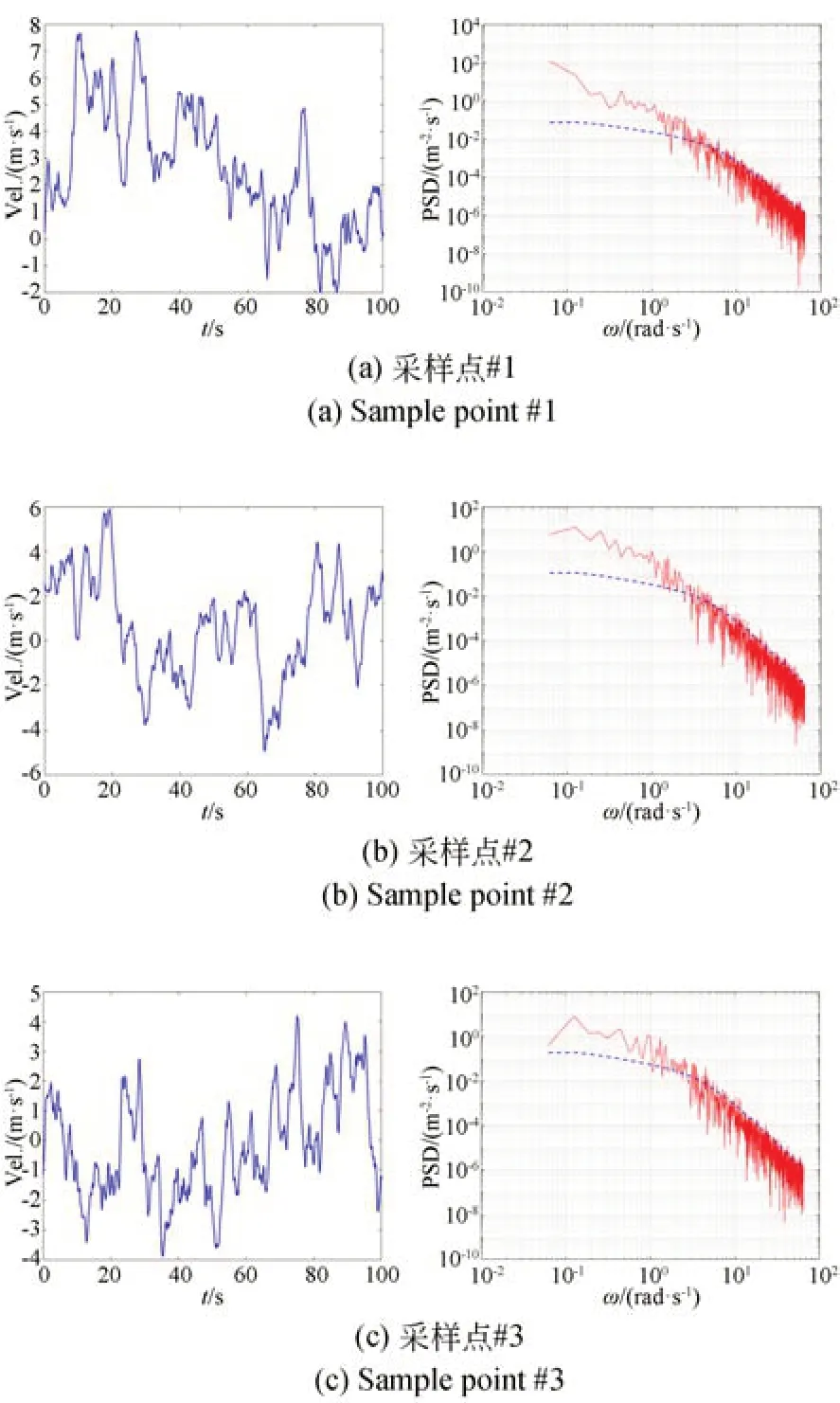

图6 主镜各个采样位置的风速Fig.6 Wind speed for each sample point of the primary mirror
(1)从时间历程上看,各个采样点的风速均随时间随机变化;
(2)在模拟时长范围内,各个采样点风速时程的功率谱与初始给定的Davenport 功率变化趋势基本一致,且与文献[18]给出的结论相符。
从以上结论可以看出,基于二维随机场理论而生成的风速场具有空间和时间随机性的特征,这与实际望远镜使用环境中风速的湍流特性是基本一致的,以此来模拟实际中的风速环境是合理可行的。
4.2 风扰动分析及光学性能预测
利用4.1 节给出的随机风速场,按3.3 节所述的计算方法得到平均风速10 m/s 和15 m/s 情况下风载荷时间历程数据,并加载到望远镜结构动力学模型中,即可模拟出望远镜上各个位置的风扰动响应。由于望远镜工作中主要关注光学系统性能,而光学系统主要受主、次镜的镜面面形以及相对位置影响,因此在性能模拟与预测时主要考虑主、次镜镜面节点位置的动态变化情况。根据离散节点位置变化,采用非线性最佳拟合的方法计算主、次镜镜面面形精度以及相对空间位置,具体计算方法可参考文献[19],并以此来评估风扰动对望远镜的影响。
在风扰动模拟时,将主镜与次镜及桁架分开考虑,这样有利于详细分析主镜与次镜及桁架之间的相互耦合关系。在主镜单独作用风载荷情况下,主、次镜镜面面形精度变化如图7 所示,光轴角度变化如图8 所示,主、次镜相对位置偏差如图9 所示。
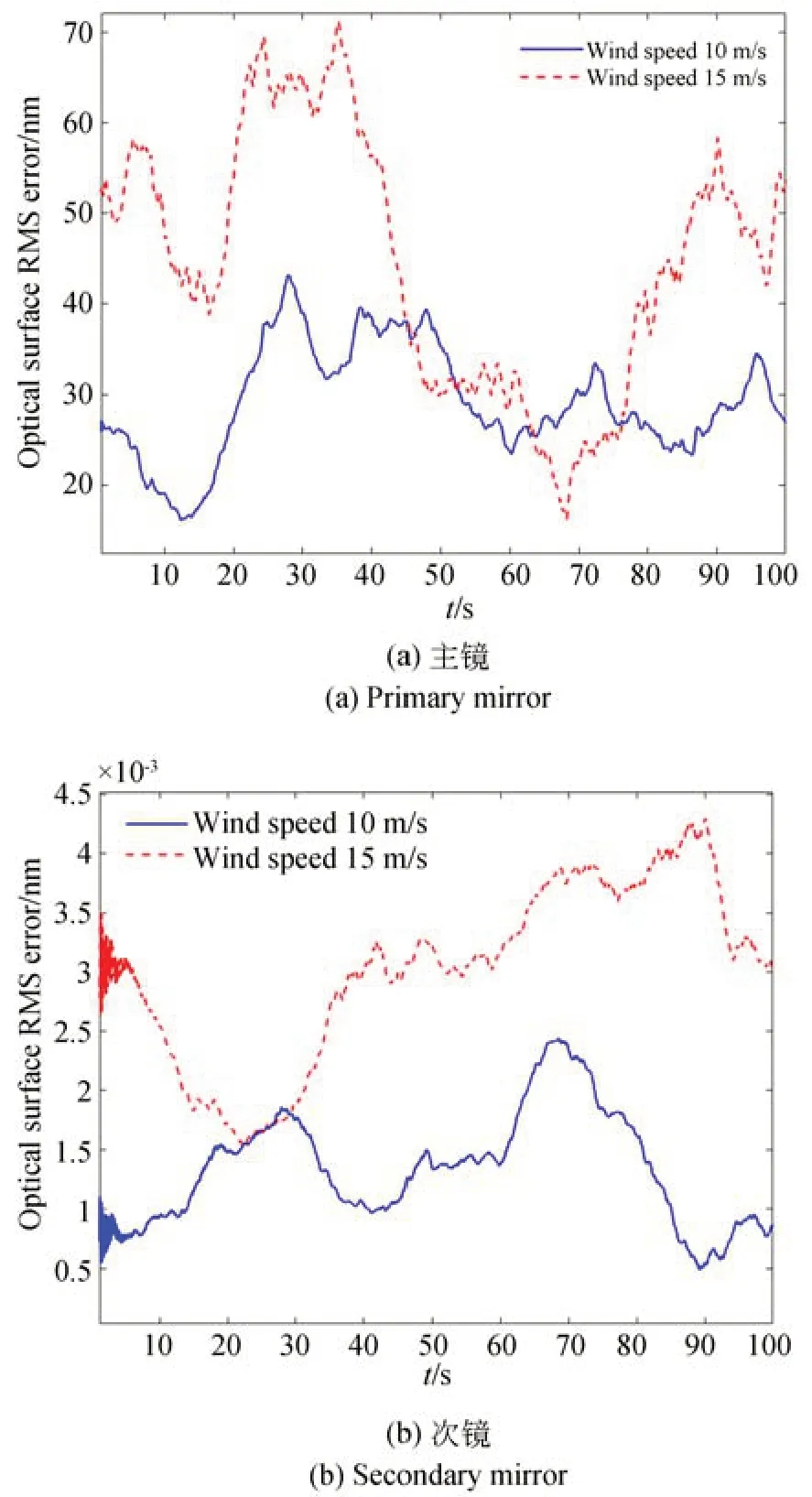
图7 主镜和次镜镜面面形精度-主镜单独加载Fig.7 Surface precision of the primary and secondary mirror-primary mirror loaded separately

图8 主镜和次镜光轴角度-主镜单独加载Fig.8 Optical axis perturbation of the primary and secondary mirror-primary mirror loaded separately
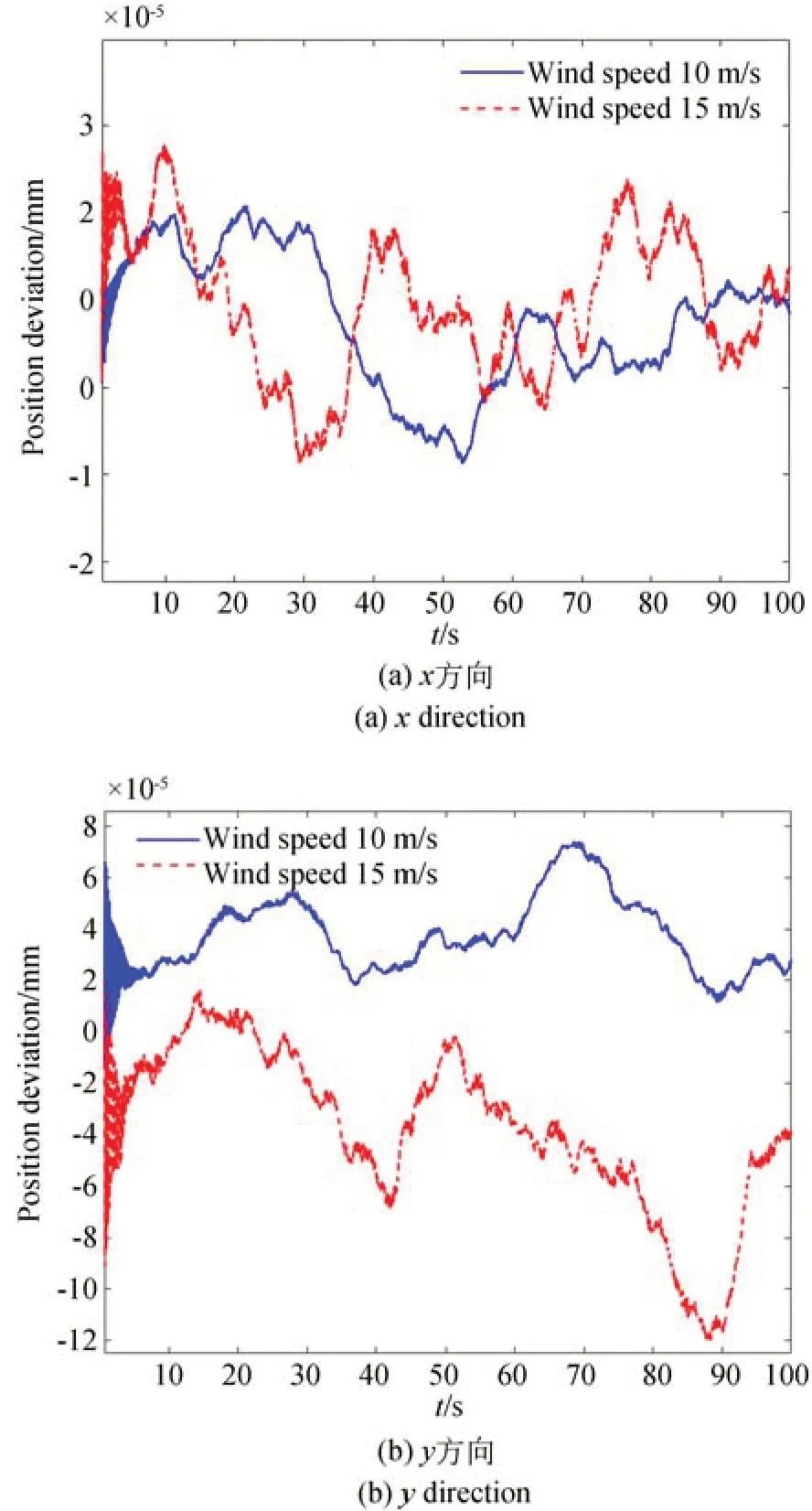
图9 主次镜位置偏差-主镜单独加载Fig.9 Position deviation of the primary and secondary mirror-primary mirror loaded separately
在主镜单独作用10 m/s 和15 m/s 风扰动载荷情况下,主镜的面形精度影响很大,最差面形精度分别达到了45 nm 和70 nm,而次镜面形精度基本不受影响;主、次镜光轴角度偏差最差时分别达到0.15″和0.25″,对相对位置偏差几乎没有影响。
在次镜及桁架单独作用风载荷情况下,主、次镜镜面面形精度变化如图10 所示,光轴角度变化如图11 所示,主、次镜相对位置偏差如图12所示。
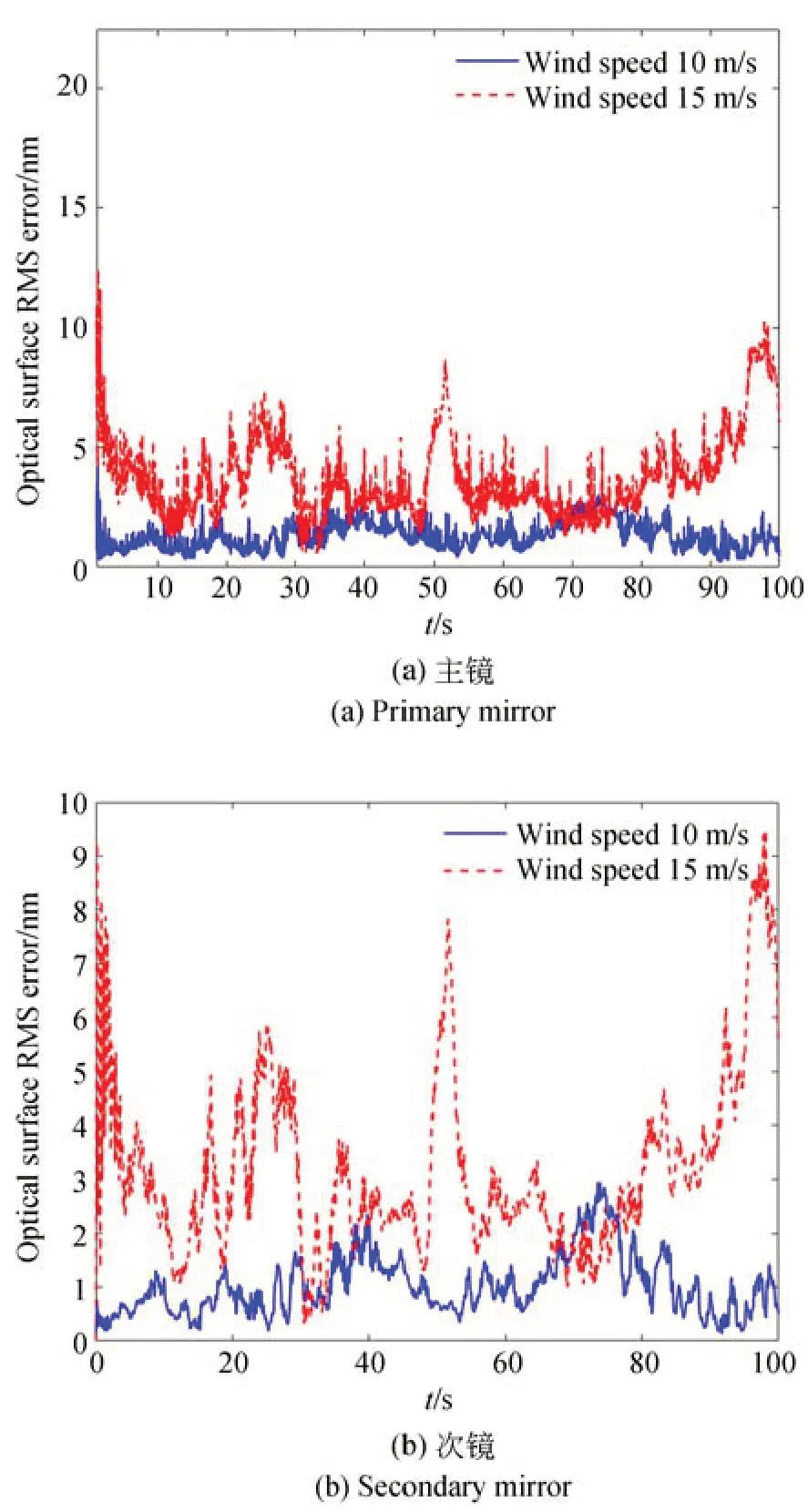
图10 主镜和次镜镜面面形精度-次镜及桁架单独加载Fig.10 Surface precision of the primary and secondary mirror-secondary mirror and truss loaded separately
在次镜及桁架单独作用风载荷情况下,主镜面形精度受影响相对较小,在整个仿真时段均在5 nm 左右;而次镜面形精度变化同样很小,原因在于次镜口径较小;主次镜光轴角度较前一种工况增加幅度很大,初始阶段最大偏差接近8″~10″,剩余阶段在4.5″以内,但波动频率明显提高;同样主、次镜y向相对位置偏差增加幅度很大,分别达到了0.1 mm 和0.2 mm。对图11 和图12(b)所示数据进行FFT 变换得到频谱如图13 所示。从频谱曲线中可以看出,风扰动载荷对望远镜的影响集中在低频部分,约0~5 Hz 区域,高频分量的影响较小。
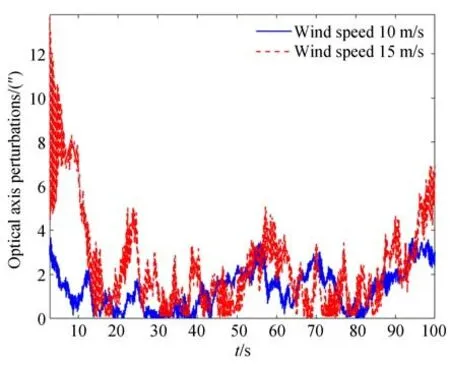
图11 主镜和次镜光轴角度-次镜及桁架单独加载Fig.11 Optical axis perturbation of the primary and secondary mirror-secondary mirror and truss loaded separately
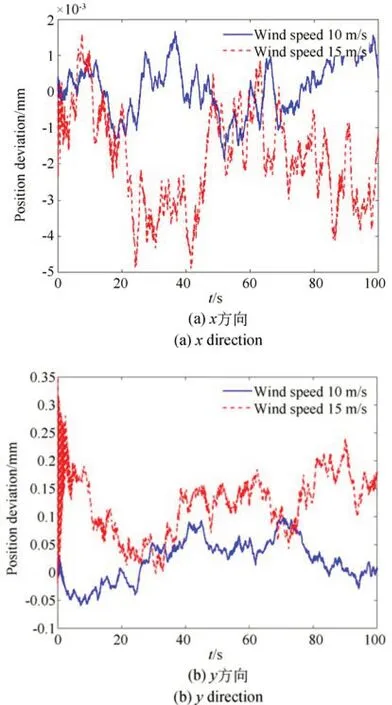
图12 主镜和次镜位置偏差-次镜及桁架单独加载Fig.12 Position deviation of the primary and secondary mirror-secondary mirror and truss loaded separately
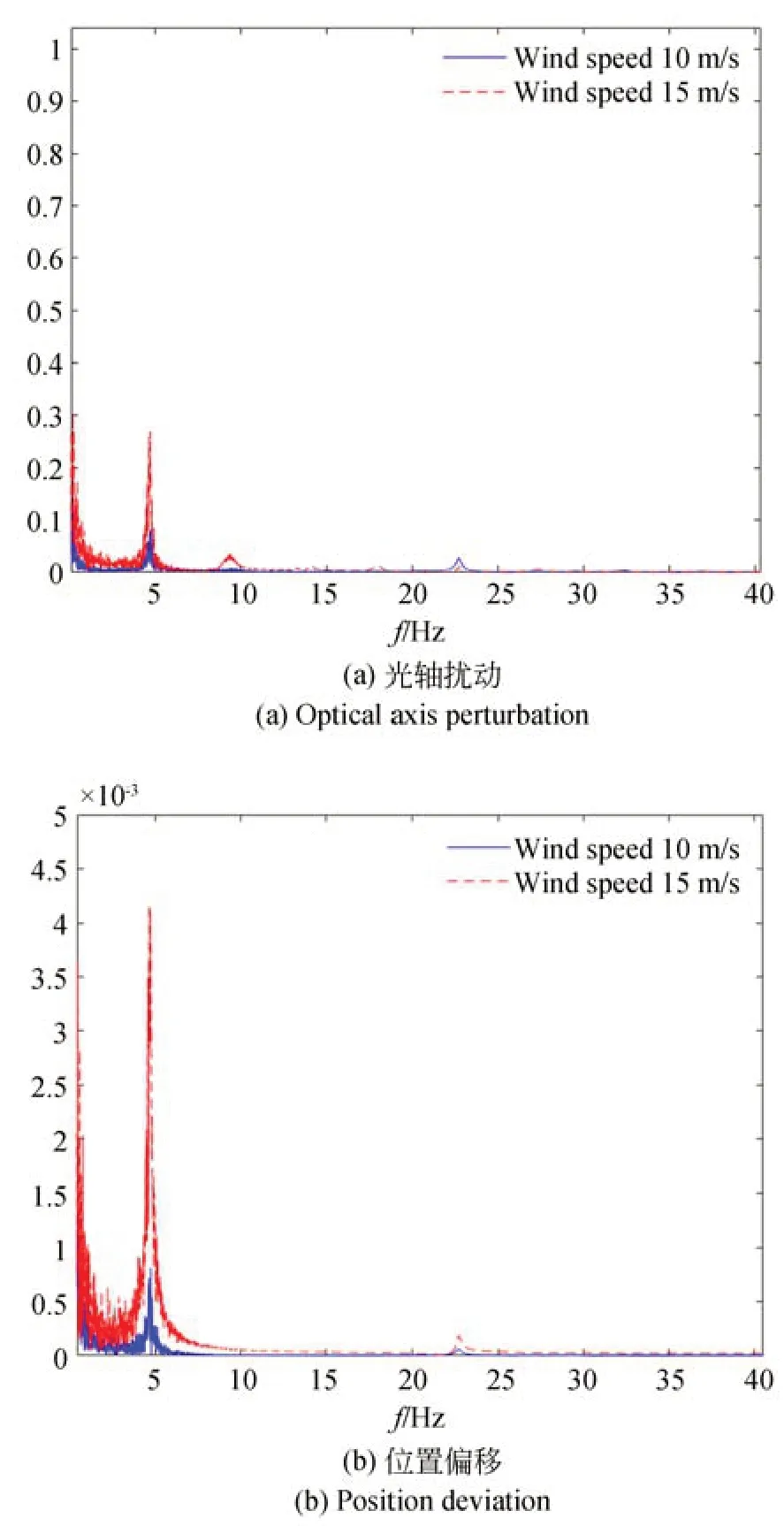
图13 主次镜偏差频谱-次镜及桁架单独加载Fig.13 Frequency spectrum of position deviation between primary and secondary mirror-secondary mirror and truss loaded separately
从以上两种情况下的分析结果对比中可以得出以下结论:
(1)由于次镜口径较小,相对刚度较大,风扰动对次镜面形精度影响较小;
(2)主镜面形精度变化主要来源于作用在主镜镜面的风载荷,受次镜及桁架的影响较小,即主、次镜相互耦合较小;从望远镜结构特征角度看,主镜连同主镜室以及桁架分别连接在四通下表面和上表面,而四通本身刚度很大,因此相互耦合不明显的结果是合理的;
(3)次镜及桁架单元作用风载荷时,主、次镜光轴角度偏差以及相对位置偏差明显增大,将会导致望远镜光学系统成像抖动和模糊。
5 结 论
本文针对大型地基光学望远镜系统性能受风扰动影响显著的问题,研究了风扰动的时程模拟方法并对望远镜在风扰动下的性能进行预测。利用有限元方法及模态变换,建立了望远镜结构动力学模型。基于二维空间随机场,提出望远镜圆顶内风速的时程模拟方法,此方法可以表达空间和时间频率范围内几乎连续的随机场。对2 m口径望远镜的仿真分析结果表明:在外界平均风速10 m/s 和15 m/s 情况下,随机风扰动作用在望远镜主镜上会造成主镜面形变差,分别造成最大接近45 nm 和70 nm 的面形误差;作用在次镜及桁架上的风扰动主要造成低频0~5 Hz 光轴角度误差及主、次镜相对位置偏差;主、次镜之间相互耦合效应较小。
