阵列式扰振力测量平台及其测量策略

周成波，夏明一，张恩阳，徐振邦

（1. 中国科学院 长春光学精密机械与物理研究所 空间机器人工程中心 空间机器人系统创新研究室，吉林 长春 130033；2. 中国科学院大学 材料与光电研究中心，北京 100049）

1 引 言

空间光学载荷在对地观测和深空探测等领域有着重要的应用，特别是对于巡视视场为哈勃望远镜300 倍且质量可达15 000 kg 的中国空间望远镜，在需要长时间曝光的凝视工况下，对其指向稳定度（LOS）的要求较高，所以对微振动指标的要求更为严苛。因此，为了探究微振动对望远镜系统的影响，研究空间望远镜中振源的扰振特性就显得尤为重要。特别当面对大型的航天器，其活动部件越来越大时，基于结构耦合的扰振机理也越来越复杂。目前，大型航天器调姿机构多以6 个为一组，加上工装其质量可达1 000 kg以上［1-4］。因此需要一种振源扰振力地面测量系统，能够在台面尺寸、刚度、精度以及负载能力上满足测量大型航天设备振源的要求。

目前，对于振源（如反作用飞轮、致冷器、数传天线以及快门等）的地面测量多采用压电式结构进行扰振力测试。其中以Gough-Stewart 构型的测量系统最为常用［5-9］，但其松散的结构会明显降低平台的刚度，当振源的质量及规模相对较大时，这将会导致在测量期间振源与测试系统的结构耦合［10］。除此之外，振源的微振动地面测量多采用四点式构型，如Li 等人［10］设计的用于大载荷的压电式六维力传感器，采用了四点冗余并联式的构型，通过每个压电陶瓷的轴向与剪切输出进行空间解耦可以得到空间六维力，由于采用了静态标定的方式，因此没有考虑结构耦合的影响。在市面上微振动测量平台中，最常用的瑞士奇石乐（Kistler）公司的多维力测量平台也采用这种四点式的布局方式。Xia 等人［11］设计了一种新型的六维广义力测量平台，其采用了8 个传感器，较大程度地提高了平台的刚度和负载能力，该设计在整体上还是属于四点支撑结构，因传感器数量的增加，刚度和承载能力都有了提升，但进一步提升的难度非常大，同时不可避免的引入了较多的系统误差。Durand 等人［12］设计了一种用于连接扳手的测量传感器，其中的传感器由6 个压电圆柱体组成，压电圆柱体安装并固定在两个板之间的不同方向上。上述的压电式力测量系统根据不同的工作环境和测试要求具有不同的结构形式和设计原理，在设计中可以只对个别参数进行设计，存在较大的设计空间。但对于高精度、大负载、高刚度的测量要求，如航天器复杂振源的地面测量，以上方式就很容易造成负载能力、刚度和精度之间的设计冲突。为了提高平台刚度和承载能力，可以增加平台和基础之间的并联环节，但过多增加可能会引入非线性项，传感器数量增加会引入明显的系统误差，这是由测试原理决定的［13］。

针对以上常规问题，本文采用了一种基于阵列式布局的测量系统。首先，通过增加并联传感器的数量来提高系统的刚度和承载能力；其次，为了提高测量精度，系统根据被测振源的预振数据对平台测试特性进行分析，基于矩阵广义逆求解的方法选出最优的传感器输出通道组合，避免了过多传感器引入的系统误差，同时也降低了不同力学特性的振源对平台的影响；最后，基于选得的最优通道组的数据，通过全回归法的线性解耦算法更为精确地求解出扰振力的表达式。本文设计了三维力测量系统样机进行前期验证，以此作为六维力测量的理论可行性探索。该平台拟用于中国空间望远镜的微振动地面试验，其中被测振源可达300～500 kg，台面尺寸需要1 m×1 m 以上，关心频率段在8～800 Hz，为了更为经济方便地进行验证实验，现将样机的台面尺寸、负载能力都进行了缩小。在最后通过实验对其进行了性能验证，提出了测量平台的测量策略，在原理上验证了所设计平台用在测量大质量设备上的可行性。

2 结构设计

该测量系统的结构部分主要由负载平台、基座以及分布在两者之间的力传感器构成，如图1所示。测试期间，系统通过基座被固定在隔振平台，被测振源被安装在负载平台上的工装内以便于测试。振源开机时，扰振数据被传递到各传感器，如果能够采集到足够数量的数据，就可用于被测振源扰振力的解算。

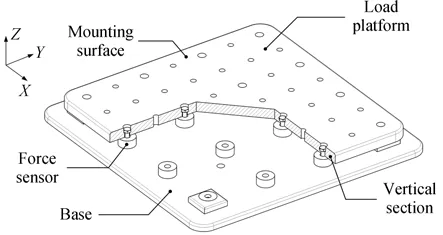
图1 阵列式测量系统结构Fig.1 Structure of the array measuring system

综合考虑优化空间及现有条件，测量系统的传感器采用4×4 阵列式的基本构型，足够多的并联环节可以保证台面尺寸、平台刚度及承载能力等参数具备较高的上限，其中力传感器采用力环形 式（Kistler，9134B，Sensitivity：-3.8 pC/N，Range：26 kN），预紧力矩在15～25 N·m 之间，传感器数据用于解算Mx、My、Fz。其中，Mx、My、Fz分别表示扰振力解耦后对x轴、y轴的力矩和沿z轴的力。

由于承载能力和分辨率主要由基本构型及传感器自身属性决定，在对本样机进行有限元分析过程中主要需要考虑的是其刚度特性。为了增加优化空间，负载平台和基座都采用了薄板的形式，并建立有限元模型如图2（a）所示，该模型通过Altair. Hypermesh 采用1/4 对称式建模方法，单元类型主要为六面体网格（99.53%），节点数为10 531，单元数为6 803，MPC 数为0，各部件通过节点耦合的方式连接。从MSC.Nastran 仿真结果来看，平台的基频为1 174.6 Hz，其二阶固有频率为1 2279.4 Hz，而一般不希望引起耦合作用的频率段在8～800 Hz 之间，设计平台的固有频率不在此范围之内；反之，会引起振动放大。如图2（b）所示，用同样的方法对传感器为2×2 分布的测量平台进行仿真，得到其基频和二阶固有频率分别为362.7 Hz 和646.5 Hz，远低于传感器为4×4 阵列分布平台所对应的频率。由以上仿真结果可得，所设计平台刚度较2×2 分布式测量平台更大，引起的结构耦合作用更小［13］。此外，与传统构型相比，所提出的阵列式布局平台刚度设计更简单，特别是对负载平台的设计要求大大降低。

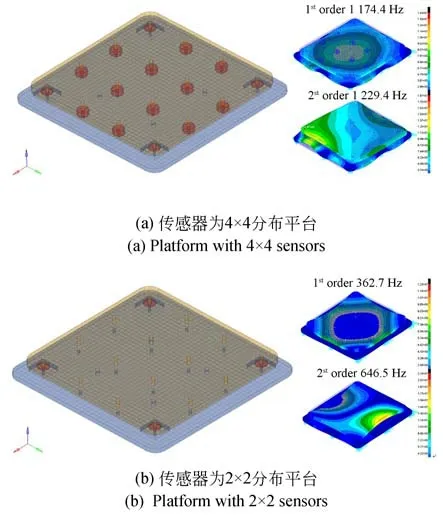
图2 阵列式测量系统有限元模型及前两阶振型Fig.2 Finite element models and the first two order modes of systems

基于以往的研究结果可知［11］，冗余观测及标定会导致测量结果中引入明显的系统误差，所以阵列式平台在常规的观测方法下，即全部传感器参与响应，并在不考虑环境噪声的前提下，其测试精度会大幅下降。所以将在每次扰振力测试前从16 个传感器中选取最优的传感器组进行扰振力的解算，即进行预振选取最优通道组，这样就可以在保证阵列式测量系统结构特性（台面尺寸、刚度、承载能力）优异的前提下，确保测试精度。

3 三维扰振力求解

在实际的每次测量中，环境噪声是随机变量，系统误差和随机误差所占比重无法预测，被测振源的质量、扰振特性、安装位置，也是随机变量，平台内部传感器对被测振源的敏感程度也无法预测，此时系统的传递函数不是唯一确定的。所以需要在每次测量前通过预振模式对以上特性进行预估，并选出用于解算的最优通道组合。

为了预估被测振源的扰振特性，需要对被测振源进行预振。首先将被测振源安装在密封工装之内（文中并未使用振源，用力锤代替进行实验），每次预振时均用力锤作用在工装的固定位置1，2，…，9 点，得到时域力输入信号Fh（tk）和16路传感器的时域响应信号Uih（tk），i=1，2…，16，i为传感器通道数；h=1，2，…，9，h为预振位置；tk=1，2，…，tk为采样时间点，以上数据是基于某一采样频率测得的离散数据。基于该数据，首先对数据的信噪比（SNR）进行评价以选择观测方式，参见式（1）可用于评估环境噪声。

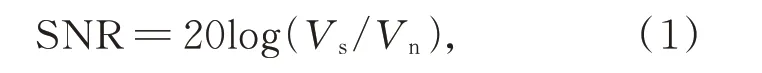
其中：Vs为扰振数据RMS 值，Vn为检测环境噪声RMS 值。该信噪比用于评估信号随机误差成分是否满足常规测试条件（大于20 dB），以确定参与传感器数量m＞3 的冗余观测或者m=3 的常规观测方式。当环境噪声中随机成分过多时，拟通过适当增加参与传感器数量以降低随机误差，为了不过多引入系统误差，环境良好时应采用非冗余的观测方式。

因为微振动的幅值和频率分布较广，所以本文的微振动测量基于频谱分析。由离散傅里叶变换公式（2）可得频域力输入信号Fh（ω）和16 路传感器的频域响应信号Uih（ω）。

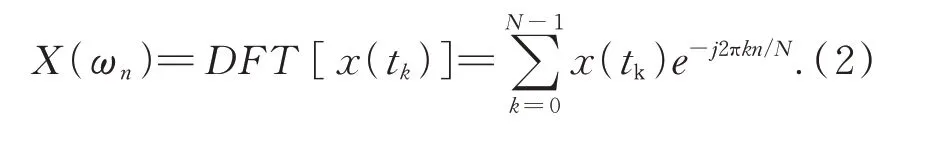
基于上述内容，在选择了观测方式之后，进行三维力的动态解耦及最优通道组的选择。假设环境噪声较小，拟选用非冗余观测方式，即m=3（冗余观测的三维力解耦仅在矩阵维数上存在差异，能从非冗余观测的解耦推广得到），任意选 取 通 道 组 为nl，nm，nn，其 中nl≠nm≠nn，则 选 取用于计算的电压输出值为Ulh（ω），Umh（ω），Unh（ω），h=1，2，…，9，上述数据可用于解耦三维力Mx、My、Fz。用 于 传 感 器 三 维 力 解 耦 的 方 法 较多［14-16］，但为了节省选取最优通道组时的计算机计算资源，并考虑到Matlab 中计算矩阵的优越性能，所以在前期选取最优通道组时使用基于求解矩阵广义逆的解耦算法来进行求解。

此时用向量F（ω）=［Mx（ω）My（ω）Fz（ω）］T表示频域输入三维力，用Ulmn（ω）=［U1（ω）U2（ω）U3（ω）］T表示任意选取三路输出的频域电压信号，Blmn（ω）为常数误差矩阵，则三维力与电压之间的关系为：

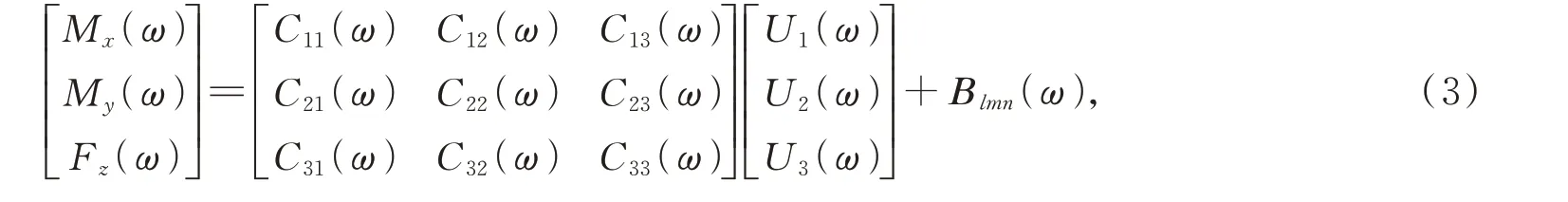
即：

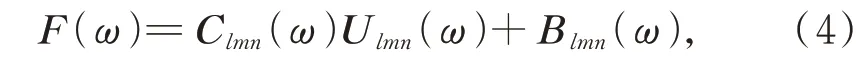
其中，F（ω）、Ulmn（ω）为3×hi矩阵，hi代表预振位置，一般来说hi≥3；Clmn（ω）为平台的动态标定矩阵。为了使指标J=Blmn（ω）TBlmn（ω）为最小，此时标定矩阵Clmn（ω）可以通过求广义逆矩阵的方式得到：

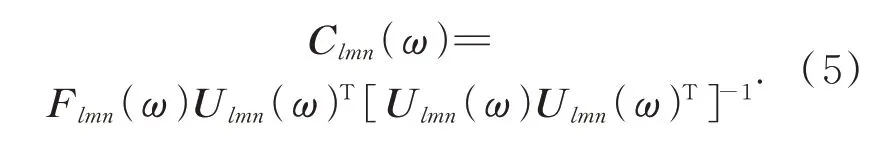
由此，可得到任意三个通道的Clmn（ω）。尽管通过求广义逆矩阵来计算解耦矩阵的方式没有考虑电压矩阵为0 时的偏置值，使得解算存在一定的误差，但在最优通道组选取时，如此标定矩阵C的求取计算量更小、耗时更少、更为快捷。

将求广义逆得到的C316个动态标定矩阵Clm（nω）分别与对应电压输出矩阵Ulm（nω）相乘得到C316个力矩阵的计算值Flmn（'ω），即力估计值：

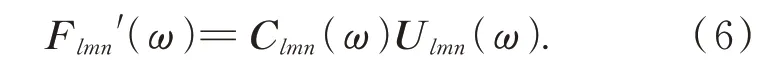
为了得到最佳三个通道数，即力计算值Flmn'（ω）与力输入值F（ω）的差值最小，建立如下目标函数：

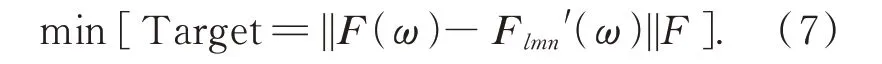
基于Matlab 遍历16 路传感器输出数据的所有组合，并结合公式（7）可得使误差最小的通道组合nb1、nb2、nb3。

为了实现更为精确的三维力解算，基于最优通道组nb1、nb2、nb3的实验数据U1（ω）、U2（ω）、U3（ω），使用了基于全回归法的线性解耦算法［17］（冗余观测方式m＞3 下的解耦同样推广可得）。

假设z方向上的力Fz（ω）与三个最优通道的电 压 值U1（ω）、U2（ω）、U3（ω）的 线 性 关 系如式（8）：

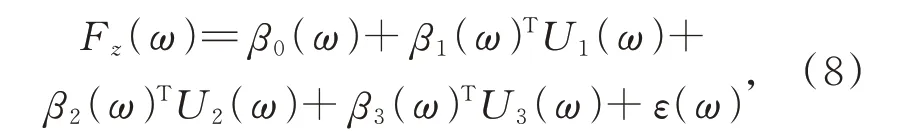
式（8）为回归方程，其中β0（ω）、β1（ω）、β2（ω）、β3（ω）为回归系数，ε（ω）为剩余误差。根据Fz（ω）、U1（ω）、U2（ω）、U3（ω）的h组测试数据可计算回归系数。将测试数据带入式（8），可得：

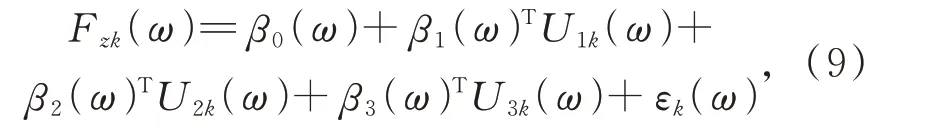
其中：k=1，2，…，h；εk（ω）为每次测试的误差。设βi（ω）（i=1，2，3）的估计值为bi（ω），εk（ω）的估计值为ek（ω），则（9）式可以写为：

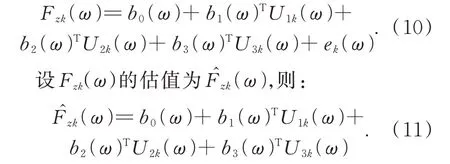
由此，b0、b1、b2、b3的值可通过式（12）、式（13）求得［17］：

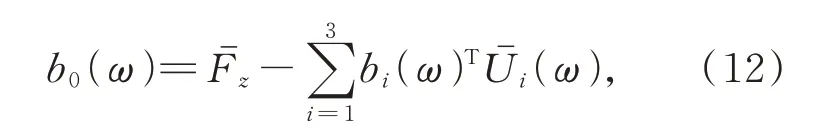
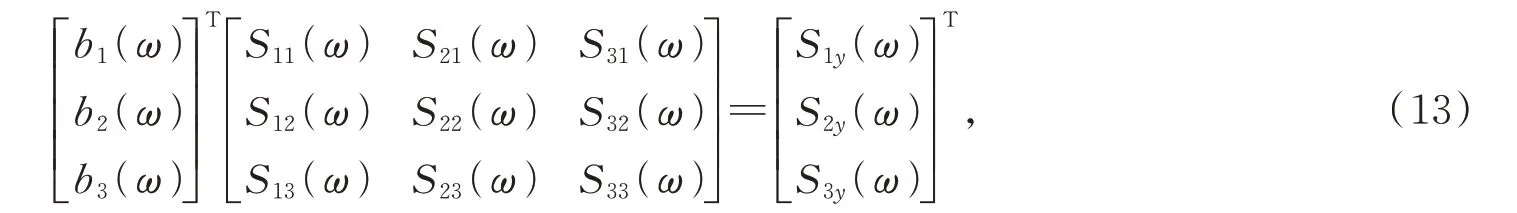
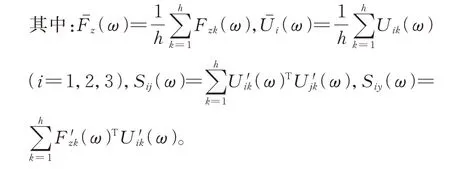
则可得到（11）的具体表达式，同理分别可得Mx（ω）、My（ω）关于U1（ω）、U2（ω）、U3（ω）的表达式。若想要时域下的力信号，将得到的频域下的三维力经离散傅里叶逆变换可得到：

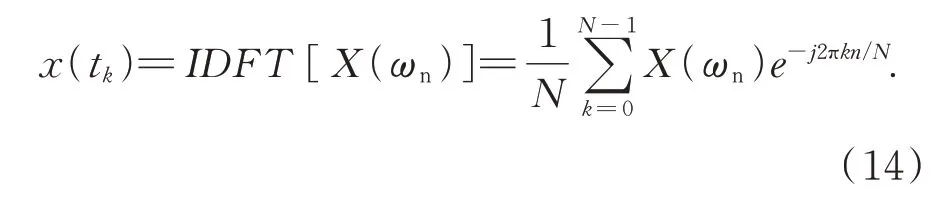
至此，从16 个传感器中选取了最优电压输出通道组，并用最优通道组的测试数据得到更为精确的扰振三维力表达式。

4 实 验

实验主要包括：验证阵列式平台的刚度及动态线性度；验证振动实验最优传感器组合的选取和三维力表达式的求解过程，即预振实验；完成扰振力测试，检测动态力测量精度，验证测量平台及测量方式的可行性，并验证以上理论的正确性。

4.1 固有频率及动态线性度测试实验

图3 为动态力学性能测试实验系统实物图，系统主要包括加载工装、电荷放大器、数据采集设备、测力平台样机、分析系统（精度：±0.1 dB；VRAI820-24bit，M+P，Germany）以 及 力 锤（086C03，PCB；灵敏度：2.25 mV/N；分辨率：0.02 N-rms；测量范围：±2 200 N-pk）。

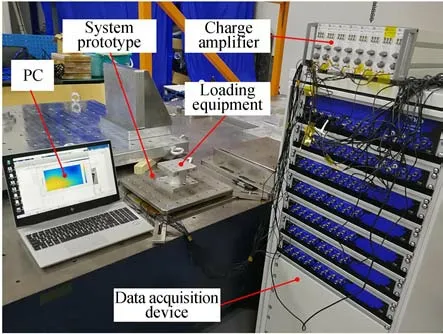
图3 测试系统Fig.3 Test system

其中，测力平台的传感器分布如图4 所示，为4×4 的结构布局形式，在轴线处并没有布置传感器，以防止“不能测得扭矩”的现象出现并使得解耦 失 败 ，图 中a1=b1=0.15 m，a11=b11=0.05 m［11］。

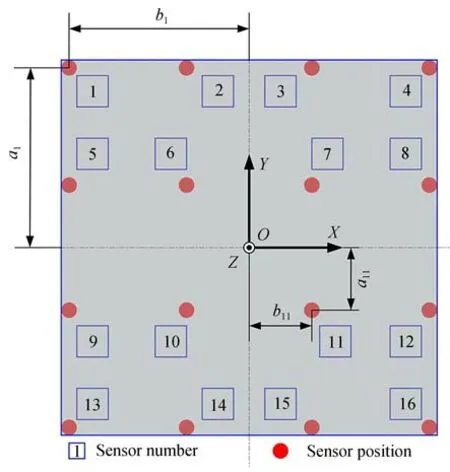
图4 传感器位置分布Fig.4 Sensors location distribution

实验首先测量了系统的固有频率。通过力锤输入宽频冲击信号，可以得到系统各传感器的频响函数曲线。图5 展示了6 和9 号位置传感器的频响函数曲线。为了原理上验证动态线性度，通过输入不同峰值的宽频冲击，并检测频响函数曲线的重合度，同时通过该曲线，平台的基频也可以被得到。可得系统基频为1 174 Hz（采样频率：8 192 Hz，有效带宽：0.062 5 Hz～3 200 Hz），由前文可知系统仿真基频为1 174.6 Hz，两个值非常接近，表明阵列式系统在仿真刚度设计时的优势，利于耦合测试需求下的系统设计。此外，样机的负载平台很薄，通过加强设计，其刚度可以进一步提升。基于传递函数的重合度，通过不同频段曲线相互之间的相对误差来表征动态线性度，由式（15）可算得：各通道的动态线性度都可以保证在0.1%FS 以内，其中i=1，2，3；j=1，2，…，nfft。同时，也可以在图5（b）红框中看到由于工频（50 Hz及其倍频）的影响，滤波后频响函数产生了平移，在现有条件下难以避免。

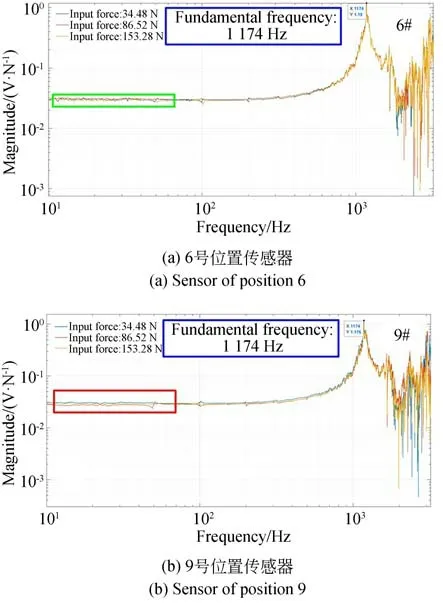
图5 系统频响函数Fig.5 Frequency response function of the system

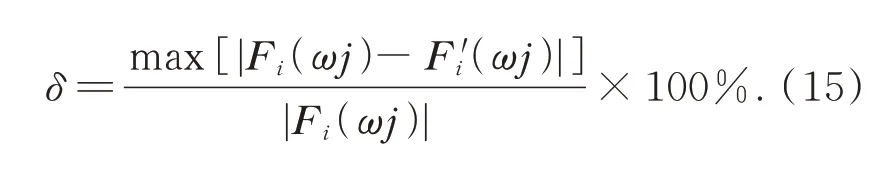
4.2 预振实验

为了获得最优通道组，从而进行三维力表达式（11）的求解。通过试验方法验证了预振流程。

如图6 所示，工装安装在平台上的2～7 位置处。其中，位置2～7 表示工装安装的对角线位置为传感器2 和7。如图7 所示，工装上有九个加载点，可通过力锤对工装在加载点上进行加载。本实验取1、5、9 三点输入宽频冲击力（采样频率为2 048 Hz，采样时间为16 s，有效带宽1/16～800 Hz，标定有效系数为2.56），选取h=3，即每点加载3 次，每点3 次的力锤反馈力取平均后作为输入标定力，以降低人为随机误差。同时16 个通道的电压输出值也取平均后作为每路通道的输出值。照式（1）计算后，选定传感器数m=3 的非冗余观测方式。经式（2）可得频域下的输入信号和响应信号。

图6 工装放置示意图Fig.6 Diagram of tooling placement

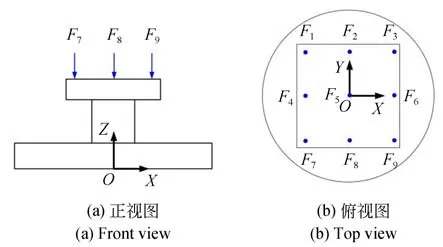
图7 标定过程的加载点布局Fig.7 Layout of the load points for the calibration process

由于所施加的载荷并不在平台安装面上，需将1、5、9 三点的载荷转换到平台安装面的形心处，即：

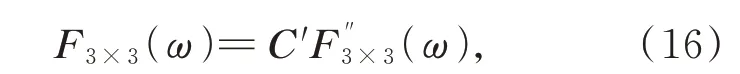
其中：F3×3(ω)表示频域下等效到平台安装面形心的载荷；F''3×3(ω)表示频域下实际加载载荷，是一个对角阵，矩阵中的F''ii(ω)等于1、5、9 三点上3 次加载载荷的平均值；C′表示实际加载载荷矩阵与等效载荷之间的转换矩阵。由工装的安装位置2～7 可得C′为：

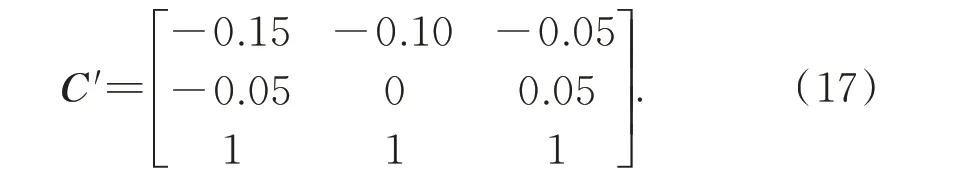
基于以上，式（3）可改写为：

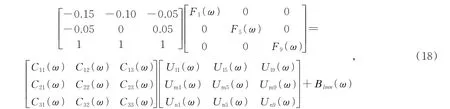
其中：F1（ω）、F5（ω）、F9（ω）表示通过点1、5、9 输入的力。Uli（ω）、Umi（ω）、Uni（ω）（i=1，5，9）表示任意三个通道组对应于1、5、9 三点的电压输出值。每个元素Cij长度为32 768。

式（18）即可写为：

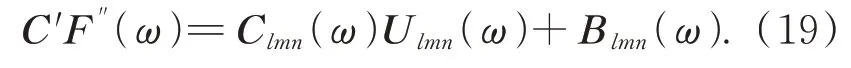
由式（19）可解得任意三个通道的标定矩阵：

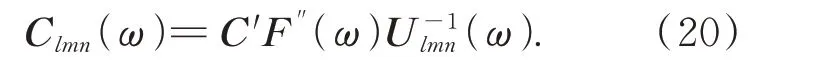
通过Matlab 的遍历搜索，找到满足（7）式的通道组合，分别为第3、6、7 通道。

将第3、6、7 通道的实验数据带入式（12）、（13）可得本次扰振力更为精确的测量表达式（11）。

4.3 扰振力测试

最后，测试了系统的扰振力测量精度。工装安装位置应与预振测试一致，如图6 所示。本测试在工装的2 点输入冲击力。

图8 为基于全回归法的线性解耦算法下平台解算得到的扰振力与输入扰振力的对比图，其中（a）为Fz数据，（b）为My的解耦数据。从图中可以看出，所设计的阵列式平台刚度特性比较稳定，受传递函数平整度影响，关心频段没有峰值，解耦结果更为准确，拟合度更高。平台灵敏度及承载能力则主要由传感器确定，灵敏度可达1 000 mV/N，测量范围达到416 kN（根据并联分载原理：26 kN×16=416 kN）。

图8 位置2-7-2 输入力与解耦力对比图Fig.8 Comparison of measured forces with input forces under position 2-7-2

表1 中列出了两种算法下8～800 Hz 内的动态相对测量误差，其中a 为求解矩阵广义逆的解耦算法，b 为基于全回归法的线性解耦算法。可得基于全回归法的线性解耦算法下的各向平均相对误差小于5%，相较于基于求解矩阵广义逆的解耦算法求得的三维力误差更小、精度更高。

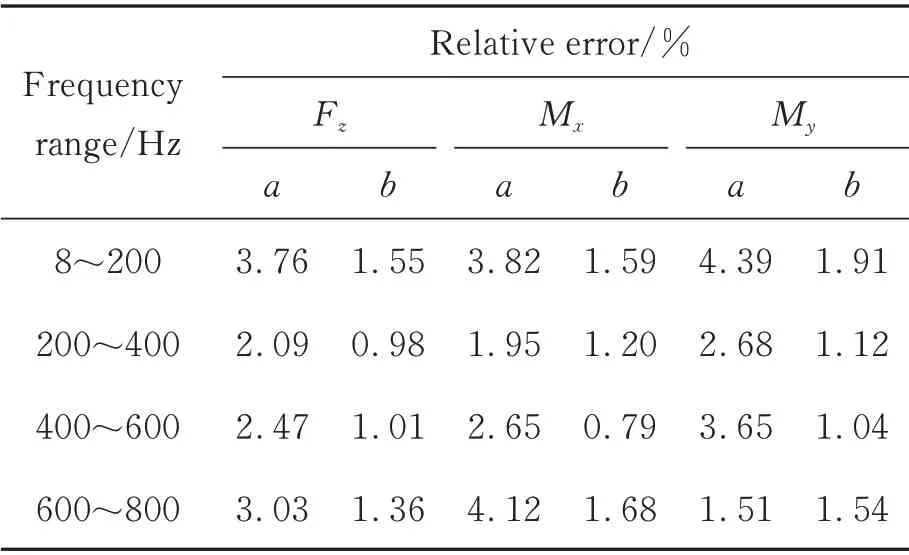
表1 两种解耦算法下8～800 Hz 内动态相对测量误差Tab.1 Dynamic relative measurement error within 8-800 Hz for two decoupling algorithms

由以上实验验证了前文理论的正确性，且所设计平台的刚度强、载荷大、精度高。

5 测量策略

经实验验证了所述测试方法的可行性，故提出如图9 所示的测量策略：

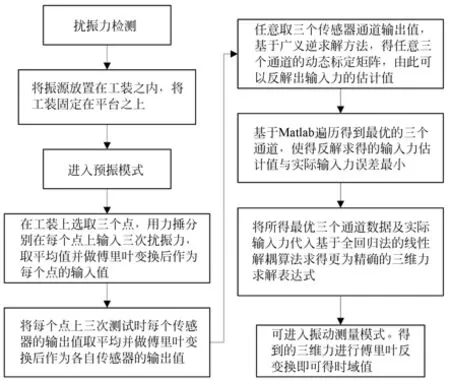
图9 测量策略流程图Fig.9 Flowchart of measuring strategy

6 结 论

本文提出一种基于阵列式传感器分布的扰振力测量系统，可用于航天器中大型振源或振源组件的扰振力地面测量实验。该系统通过阵列式的并联环节有效地提高了系统的台面尺寸、刚度及承载能力；并基于实验验证提出了一种测量策略，提高了系统的测量精度。样机的实验结果表明该系统具备较高的承载能力和刚度上限（样机基频为1 174 Hz，承载能力可达416 kN）；在8～800 Hz 范围内，各向平均相对误差低于5%。该研究结果证明阵列式测量平台及其测量策略具备可行性，可适用于各类振源的扰振力测试。