聚焦参量阵原频声场抑制方法的研究

夏靖杰，冯海泓，黄敏燕，洪 峰

(1. 中国科学院声学研究所东海研究站，上海 201815；2. 中国科学院大学，北京 100190)

0 引 言

在水声工程领域，参量阵凭借只需小孔径换能器即可获得高指向性、低频信号的优势，广泛应用于水声通信、海底掩埋物和底质探测等场景[1-3]。

参量阵的基本原理简述如下：受到热粘滞介质的非线性作用影响，原频信号在传播过程中能量会向低频和高频转移，进而有新的频率分量产生。差频信号兼具低频的穿透能力和与原频相当的指向性，是参量阵的目标信号。由于差频信号是非线性作用的衍生产物，因此原频和差频信号转化的效率很低，转换效率长期以来不足1%[4]。

为提高参量阵的差频信号能量，目前有两种主流的解决方案：(1) 提升差频声源级，比如采用提高原频声源级[2]、改变发射信号体制[5-6]等方法，以提升参量阵差频能量的转化效率；(2) 通过改变参量阵辐射面结构[7-9]，比如使用聚焦换能器或基阵，使差频能量集中在主瓣位置，同时也改善了基阵的指向性，抑制了原频信号的旁瓣。已有相关的研究有：Merklinge发现改变原频信号包络能使得参量阵差频转化效率在理论上最多能提高6 dB，其中最佳包络为矩形包络[5]，采用该发射信号体制的参量阵也称为暂态参量阵或宽带参量阵。Qu等使用包络为线性调频信号的宽带参量阵，采用单通道盲源分离算法提高了回波信号的信噪比，实现海底管道的高分辨率探测[6]。Thornton等基于一种聚焦参量阵实现了富钴结壳测厚，在焦点处的-3 dB足印宽度仅为20 mm[7]。李中政[8]和李夕海等[9]分别使用差分演化算法和遗传算法对基阵的阵元数量和排列方式进行优化，尽管损失了参量阵小孔径的空间优势，但也提高了差频信号的能量。

传统的聚焦参量阵主要有三种形式：(1) 单阵元声透镜型；(2) 多阵元密排型；(3) 多阵元非密排型。本文的研究对象限定为多阵元非密排型的聚焦参量阵，和前两种类型的聚焦参量阵相比，本文讨论的聚焦参量阵有着声源级更高、非线性作用过程的物理意义更明确的优点。

在富钴结壳海底底质原位探测中[10]，为保证测量精度，探测器距离海底的工作距离约为 1.5 m。该探测器采用了多阵元聚焦技术，有效地弥补了差频信号声源级低的先天不足，但原频信号声源级也显著提高。由于传输损失有限，原频回波能量依然较强，对接收系统的高效工作带来了不小挑战。探测器接收系统的动态范围相对有限，原频和差频回波被同时接收，容易导致接收回波的波形失真。此外，在对聚焦参量阵进行声学测量时，测量设备暴露在高能量的原频声场中，对传感器提出了较高的耐压要求。一种常用的测量方法是在水听器前加一块橡胶来隔离原频信号[2]，但该方法会破坏声场，引入测量误差。对于上述工程问题，目前尚未有完善的解决方案。

抑制聚焦参量阵原频声场的研究鲜有报道，但有关参量阵扬声器主动降噪方面的研究较多，原理是利用参量阵扬声器发射一组具有与噪声振幅相同但相位相反的声波，根据声波的叠加原理，能够实现噪声的定点抑制。相关的研究有：Jessel等分析空气导管中偶极子扬声器的声场，从理论上证明了主动降噪的可行性[11]。Tanaka等使用指向性声源阵列，实现了对指定位置噪声源的定向降噪[12]。武帅兵等利用参量阵作为次级声源，实现了管道内的自适应有源噪声控制[13]。受上述工作的启发，本文从改变发射信号形式的角度出发，探索在不破坏聚焦参量阵差频声场特性的前提下，有效抑制聚焦参量阵原频声场能量的方法。

1 参量阵设计基本理论

1.1 KZK方程

KZK方程[14-15]由吸收项、衍射项和非线性项组成，能够较为准确地描述声轴附近 20°以内开角的声场。求解 KZK方程，能够准确地预测差频声场远场的位置。在工程应用中，可通过改变参量阵的发射功率，来调节差频远场距离的大小。KZK方程可表示为[14]

1.2 Berktay包络自解调理论

Berktay在Westervelt方程准线性解的基础上提出了包络自解调理论，首次把宽带参量阵引入到水声工程中[16]。假设发射信号的表达式为[4]

式中：s表示换能器的有效发射面积。

从式(4)可知，在参量阵声场远场，声轴上某一场点处的差频信号波形仅和发射信号的包络形式有关，和载波相位无关。由此可知：改变载波信号的相位，不会对参量阵差频信号造成影响。

2 聚焦参量阵原频声场抑制理论

针对本文中研究的聚焦参量阵，其设计应遵循以下原则：(1) 避免过早截断差频声场，使得差频波束宽度变宽；(2) 防止焦点处发生声饱和现象，避免不必要的能量损失；(3) 使差频声场满足叠加定理，便于原理分析和工程设计。因此，聚焦参量阵的最佳焦点应设置在阵元差频声场的远场，使得阵元各自形成差频声场的过程互不干扰。为了方便实验验证，把“轴向距离增加一倍，差频轴向声压级下降-3 dB”视作达到差频远场标志，而不严格要求焦点位于参量阵阵长[17]之外。

两阵元对称安装于同一曲面上，组成双阵元聚焦参量阵，原理图如图1所示。为双阵元聚焦参量阵设计了两种发射信号形式，把载波信号相位φ=0°作为参考相位，φ= 1 80°称为相位相反。如图 1(a)所示，根据声场叠加定理，若两阵元发射信号的载波相位相同，则焦点处原频、差频信号的声压幅值为单阵元单独作用时的2倍。如图1(b)所示，当发射信号载波相位相反时，理论上差频信号幅值不会变化，声轴上原频信号的声压幅值理论上能够完全抵消，而原频抑制的实际效果与换能器工艺和安装精度等因素有关。

图1 两种发射信号形式下的聚焦参量阵原理图Fig.1 Principle diagram of a focused parametric array with two types of emitting signals

对于两个以上阵元组成的聚焦参量阵，图2展示了原频抑制方案的实施流程。首先，通过 KZK方程的数值计算，确定单阵元差频声场远场的位置，设置聚焦参量阵的焦点位于差频声场远场，以防止声焦点处的原频信号出现声饱和现象，并使得差频声场满足叠加定理；其次，分配各阵元发射信号载波的相位，比如采用相邻阵元载波相位相反的方案，使原频声场得到抑制。

图2 聚焦参量阵原频抑制方案的实施流程Fig.2 Flow chart of primary frequency sound field suppression

3 仿真计算与实验结果

3.1 仿真和实验的准备

实验设备的组成如图 3所示，水槽尺寸为110 cm×40 cm×45 cm，发射换能器中心频率为1 MHz，带宽为200 kHz，有效发射半径为14 mm。安装曲面的曲率半径为80 cm，换能器B位于曲面的中心位置，用于测量单阵元的声场；换能器A和C对称安装，两换能器几何中心相距15 cm，用于验证聚焦参量阵原频抑制的效果。

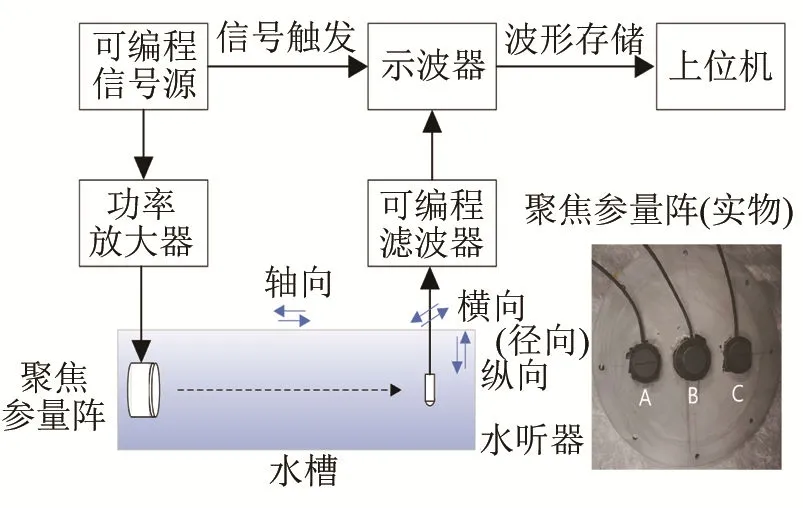
图3 实验布置示意图Fig.3 Schematic diagram of experimental setup

其他的实验设备：可编程信号源UTG4162A、两套高频功率放大器NF HAS4012和E&I 1040L、示波器Agilent DSO5014A、按倍频程校准的水听器B&K 8103和可编程滤波器NF 3628。

实验中，换能器发射100 kHz调制1 MHz的正弦幅度调制信号，信号脉宽为 10 μs，发射周期为20 ms。测量波形数据经对水听器灵敏度补偿后，使用16阶Butterworth带通滤波器，以获得200 kHz的差频信号和中心频率为1 MHz的原频信号。

基于频域法[14]计算非线性声场，采用参数如下：介质声速c0=1 480 m·s-1，密度 ρ=1 000 kg·m-3，声吸收系数 α = 2 .5× 1 0-14· f2Neper·m-1，非线性系数β=3.5，最大归一化径向距离ξmax=8，最大归一化轴向距离σmax=5，最大截断谐波数Nmax=80。对于聚焦参量阵，由于两阵元波阵面不一致，无法直接使用 KZK方程计算三维声场，故仅采用瑞利积分模型给出原频信号的声场仿真。

3.2 单阵元声场分析

单阵元轴向声场分布如图4(a)所示，声轴上原频信号的实测声压级比仿真略高，而差频声压级实测和仿真吻合度较好，实验结果和 KZK方程数值计算的结果一致性较好。此外，实验证明了参量阵的原频差频转换效率较低的结论[4]，在轴向距离0.8 m处原频和差频信号的实测声压级分别是213.2和173.6 dB、相差39.6 dB。当轴向声场呈柱面波衰减时，认为声传播中吸收和衍射的影响占主导地位，受介质的非线性作用影响较小，不再有新的差频信号产生，此时为差频声场的远场。图 4(a)中 1.6 m处的差频声压级分别为170.9 dB，与0.8 m处的声压级相差2.7 dB，基本符合柱面波的衰减规律。因此，设置聚焦换能器焦距为0.8 m是合理的。

图4(b)是对单阵元径向声场的实测和仿真的对比图。在单阵元实验中，采用的是圆形换能器B，因此横向和径向统称为径向。从图4(b)中可大致估算出原频信号的波束角约为 4.9°(实测)和 4.5°(仿真)，而差频信号的波束角约为 4.6°(实测)和 4.2°(仿真)，原频和差频信号的波束角比较接近。由于水槽尺寸限制，实测波束宽度比仿真略大，此外受阵元安装偏差等因素影响，径向声场有轻微的不对称，但不影响实验结论的获得。

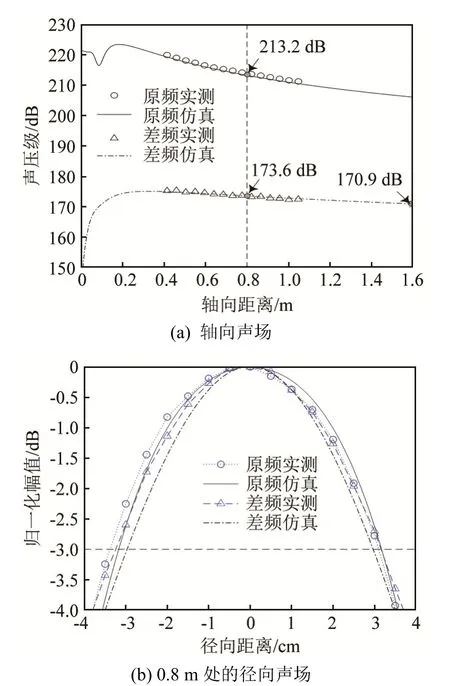
图4 单阵元的声场特性图Fig.4 Sound field characteristics of a circular transducer

3.3 声焦点处的声场验证

使用换能器A和C组成聚焦参量阵，分别为发射信号分配相位值，以验证焦点处的波形是否满足设计要求。为便于结果比对，实验中使用两台不同的功率放大器分别驱动换能器，两种发射方式下焦点处的实测波形如图5所示。

图5 两种发射方式下，焦点处波形Fig.5 The signal waveforms at the focal point under two emission modes

由图5(a)和图 5(b)可知，尽管原频信号波形存在一定差异，但差频信号波形吻合度较高，说明功率放大器更多地影响发射信号的载波，对信号包络影响较小。随着阵元同时开启，聚焦阵原频和差频信号的声压幅值翻倍，且未发生原频声饱和现象，这说明在声焦点处，有限振幅波已经衰减成小振幅波，满足仅适用于线性声学的声叠加定理。

对比图 5(a)和图 5(c)可知，当两阵元的载波信号相位相反时，焦点处原频信号幅值只有单阵元作用时的1/3，比相位一致时低13.2 dB左右。图5(d)和图5(b)则说明载波相位变化前后的差频信号波形未发生变化，实验结果和 Berktay理论“差频信号的波形只和包络有关”的结论相符。

3.4 聚焦参量阵声场的空间分布特性

声场的空间分布特性是评价参量阵性能的重要指标。聚焦参量阵载波信号相位一致时的声场特性如图6所示。图6(a)中，由于安装误差以及换能器工艺的差异，原频信号实测的声焦点位于 0.78 m处，略小于聚焦参量阵0.8 m的几何焦点位置；而差频信号的声焦点位置位于0.82 m处，比原频信号的略远。实验现象表明，声焦点附近的能量相对集中，各阵元发出的原频信号衰减成小振幅波后，再次转变成有限振幅波，产生了新的差频分量，由此导致差频声焦点位置的后移。图6(b)和图6(c)中，受阵元数量影响，聚焦参量阵焦点处的横向声场由于声波的干涉作用，声场呈锯齿状，而横向声场分布曲线更光滑。

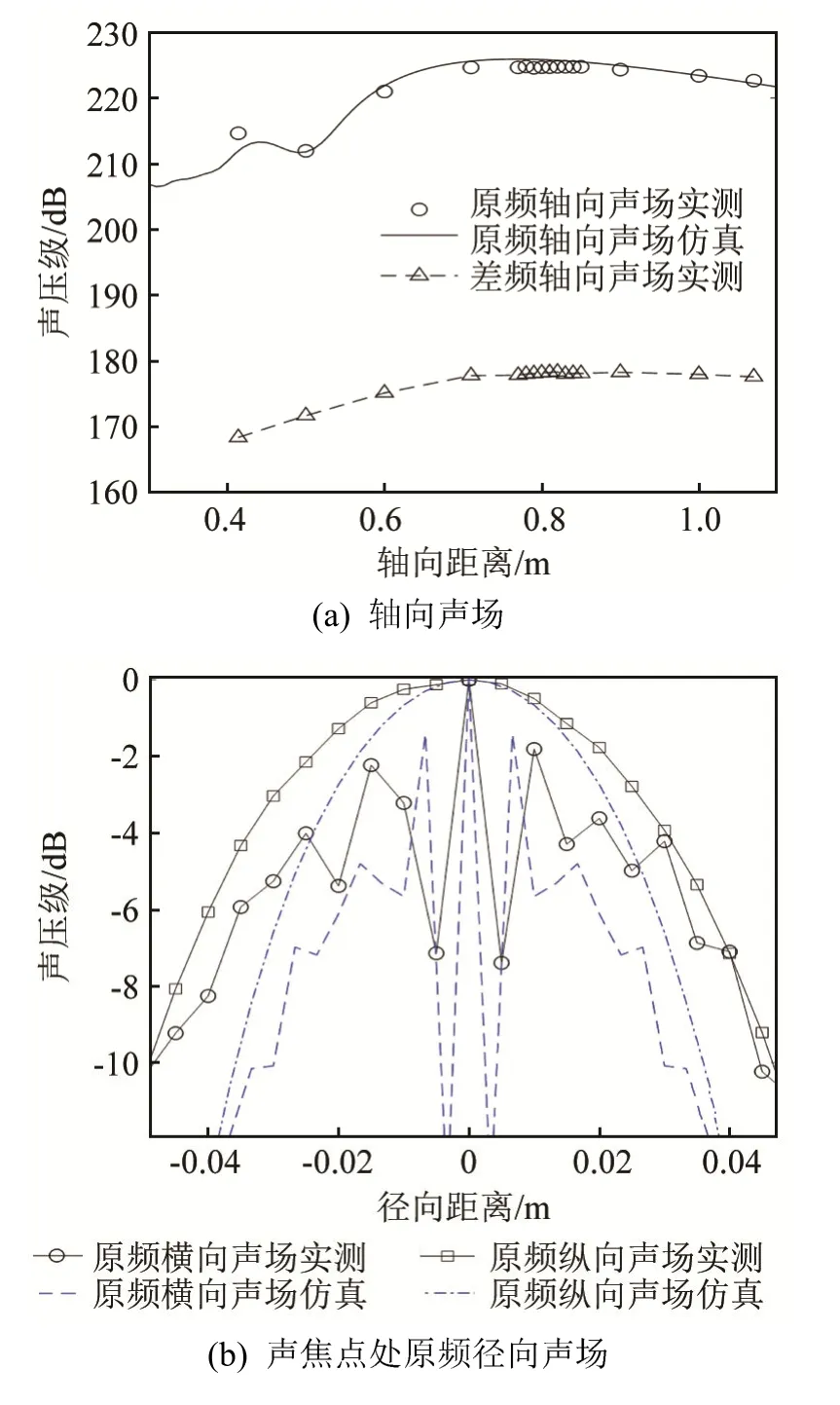
图6 发射信号载波相位相同时，聚焦参量阵声场的特性图Fig.6 Sound field characteristics of a focused parametric array when the two emitting signals in the same phase

当载波相位相反时，聚焦参量阵声场特性如图7所示。对声压归一化后，原频信号声场分布和焦点处的声场分布仿真如图7(a)和图7(b)所示，声轴上原频信号被完全抵消，焦点位置处的声场分布图中出现了关于声轴对称的正负两个声压极值。对比图6(a)和图7(c)可知，两阵元相位反向后，原频轴向声场的声压级下降明显，整体下降值在13 dB以上，而差频轴向声场基本没有发生变化。图7(d)中原频信号的横向和纵向声场大致关于声轴轴对称分布，和仿真结果相吻合。图7(e)中差频信号的轴向和径向声场和图6(c)吻合度较好。

图7 发射信号载波相位相反时，聚焦参量阵声场的特性图Fig.7 Sound field characteristics of a focused parametric array when the two emitting signals in opposite phases

综上可知，对于两种发射信号形式的双阵元聚焦参量阵，分配阵元载波相反的相位，几乎不会影响差频声场的分布，但对原频声场能起到较好的抑制作用。和图4(b)中单阵元的径向声场相比，无论是差频信号还是原频信号，两种发射信号形式的聚焦参量阵在焦点处能产生比单阵元更窄的波束，能量也更为集中。

4 结 论

本文对聚焦参量阵在近距离海底底质原位探测时原频能量过高的问题展开研究，通过对 Berktay包络自解调理论和 KZK方程深入分析后，提出了一种聚焦参量阵原频抑制方法。通过实验和仿真，对比了不同发射信号形式对聚焦参量阵声场特性的影响。结果表明：所提出的原频声场抑制方法能有效降低聚焦参量阵原频声场能量，且几乎不会影响到差频声场特性。此外，本文所提方法简单易行，能够为聚焦参量阵声学测量和工程应用提供一定的参考。

由于文中采用的是高频发射信号，波束较窄，同时两个阵元安装时保持了一定距离，使得两列波束在到达焦点前声场的相互影响较小。下一步工作将研究聚焦参量阵的阵元间距和发射信号频率对原频抑制效果的影响。

致谢在此感谢王润田研究员和童晖副研究员等人在实验器材上提供的帮助。