弹性高超声速飞行器动态面制导控制一体化设计方法
2022-03-11王建华汤国建潘玉龙陈海山
安 通, 王 鹏, 王建华, 汤国建, 潘玉龙, 陈海山
(1. 空军预警学院, 湖北 武汉 430019; 2. 国防科技大学空天科学学院, 湖南 长沙 410073; 3. 航天工程大学宇航科学与技术系, 北京 101400)
0 引 言
高超声速飞行器一般为飞行速度大于5马赫的飞行器[1],具有响应快速、突防能力强、机动性高等优势,目前已成为世界航天大国的重点研究方向。高超声速飞行器在临近空间的滑翔过程具有快时变、强耦合、强非线性和强不确定性的特点,且弹体表面烧蚀、湍流的作用以及细长的几何外形设计给飞行器带来了弹性耦合特性,这些特点都对其制导控制系统设计提出了更高的要求[2]。
制导与控制一体化(integrated guidance and control, IGC)设计能够充分考虑制导与姿控分系统的耦合特性和飞行器质心运动与绕质心运动间的交互影响,提高制导控制系统的总体性能[3-5],已被广泛应用于各类飞行器的制导控制系统。目前针对IGC设计,最常用的思路是首先建立同时包含制导和姿控分系统被控状态的全状态耦合IGC设计模型,模型同时包含视线角、飞行器姿态角、角速率等运动参数,且一般为严格反馈形式,然后再利用反步控制、动态面控制等方法求解该IGC系统,这样IGC系统设计问题就转化为包含非匹配不确定项和匹配不确定项的非线性时变系统的输出调节问题[3,6-8]。基于上述思路,针对设计模型包含的不确定性,一些研究者采用自适应方法对不确定性上界进行估计,从而对不确定性进行补偿[9-11]。此外还有一些研究者采用扩张状态观测器技术[12-17]或非线性干扰观测器(nonlinear disturbance observer, NDO)技术[18-20],对设计模型中的不确定性进行实时估计,从而实现对不确定性的高精度补偿。以上设计方法的有效性均通过仿真试验得到了验证。
针对高超声速飞行器刚体/弹性耦合的问题,国外学者将飞行器视为弹性体,通过曲线拟合的方式对气动数据进行拟合,建立了一系列弹性高超声速飞行器运动模型,如Bolende第一定律模型[21-22]、Sigthorsson模型[23-24]和Lisa模型[25]。由于反步控制或动态面控制方法的设计模型能充分考虑包括弹性耦合状态在内的不确定性影响,且其递推设计过程降低了控制设计系统的难度,因而被一些研究者应用于弹性高超声速飞行器的控制系统设计。Zong等针对纵向平面内弹性高超声速飞行器控制问题,将飞行器纵向运动分解为速度子系统、高度和速度倾角子系统以及攻角和角速度子系统,在考虑输入饱和情况下,设计自适应反步控制器,自适应估计飞行器不确定性上界并进行补偿,实现了对飞行器的鲁棒控制[26-27]。Bu等将弹性高超声速飞行器纵向运动分解为速度子系统和高度子系统,应用径向基(radial basis function,RBF)神经网络在线估计模型不确定性,设计了鲁棒自适应反步控制器,实现了对速度和高度指令的良好跟踪[28]。Cheng针对弹性高超声速飞行器控制问题,提出了两种不确定抑制控制方法,一种为自适应动态面控制方法,另一种为基于NDO的动态面控制方法,仿真结果验证了两种控制方法对速度和高度指令的良好跟踪精度[2]。
综上所述,目前关于弹性高超声速飞行器制导控制系统设计的研究,大多数是面向对飞行器速度和高度指令进行跟踪控制,缺少针对弹性高超声速飞行器IGC系统设计的相关研究。这是因为弹性高超声速飞行器模型中存在非最小相位的特点,在一定程度上阻碍了反步控制或动态面控制方法在其IGC系统设计中的应用[29]。此外弹性飞行器气动模型复杂,使得IGC设计模型难以建立。因此,本文面向弹性高超声速飞行器滑翔段IGC设计问题,首先对刚体/弹性耦合的飞行器纵向运动模型进行处理,建立了适用于弹性高超声速飞行器IGC设计的系统模型。然后分别基于自适应方法和NDO技术,设计两种动态面IGC方法,对模型中包含弹性耦合状态的不确定项进行补偿。最后开展仿真试验,验证并比较两种IGC方法的制导控制精度和鲁棒性能。本文可为弹性高超声速飞行器制导控制系统设计提供一定的理论和技术参考。
1 弹性高超声速飞行器IGC建模
1.1 飞行器滑翔段运动模型
本文在建立弹性高超声速飞行器滑翔段运动模型时,做如下合理假设:① 不考虑地球曲率的影响;② 飞行器做无动力滑翔,不考虑推力。基于Lisa模型[25],得到弹性高超声速飞行器纵向运动模型为
(1)
式中:v为飞行器飞行速率;g为重力加速度大小;θ为速度倾角;m为飞行器质量;D、L分别为气动阻力和气动升力;α为飞行器飞行攻角;ωz为飞行器俯仰角速率;Jz为飞行器俯仰转动惯量;Mz为作用在飞行器上的俯仰气动力矩;ηi为第i阶弹性状态(本文选取飞行器前三阶弹性状态);Ni为第i阶弹性状态的广义力;ξi和ωi分别表示弹性状态ηi的阻尼比和自然频率。飞行器气动模型具体形式为
(2)
式中:动压q=0.5ρv2;ρ为大气密度;S为飞行器气动参考面积;lz为气动参考长度;CL、CD分别为升力系数和阻力系数;mz为俯仰力矩系数;ni为广义力系数。系数多项式的具体形式为
(3)
式中:δe为俯仰舵偏角。为了消除非最小相位影响,该模型引入了鸭翼舵偏角δc以抵消升力项中δe的相关项,δe和δc之间存在如下关系:
(4)
式中:参数具体数值可参考文献[2]。该运动模型能够充分体现刚体/弹性耦合,本文基于该模型开展仿真试验。
1.2 IGC设计模型
图1给出了飞行器-目标的相对位置几何示意图,OB代表飞行器质心,T代表目标位置。OB-xsyszs为视线坐标系,O-XYZ为地面坐标系[5],本文设定地面坐标系原点所在经度和纬度均为0°,所在高度为0 m,x轴正方向指向正东,y轴正方向垂直于水平地面并向上。
飞行器与目标位置之间相对运动方程[5]为
(5)
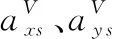
(6)
下面推导适用于弹性高超声速飞行器IGC设计的系统模型。假定在飞行过程中,飞行器的纵向体轴偏离相对视线方向的角度在一定范围内,则存在如下关系:
(7)

(8)
其中不确定项dy b为
dy b=-g cos(φ)
(9)
式中:φ=α+θ,为飞行器俯仰角。本文将气动升力系数中除去攻角一次项的剩余项(包含弹性状态相关项在内)以及气动阻力系数中的弹性状态相关项视为不确定性项,联立式(6)~式(8),整理得到:
(10)
式中:
(11)
(12)
采用类似的气动模型处理方式,并将姿态运动学方程中重力加速度相关项视为不确定项,可以得到:
(13)
式中:
(14)
类似地,基于姿态动力学方程和气动力矩模型,联立式(4)可以得到:
(15)
(16)
式中:
(17)
需要说明的是,虽然该系统模型是基于特定的飞行器运动模型建立的,但以上的模型建立思路不失一般性,可推广到其他弹性高超声速飞行器。基于飞行器运动模型的具体气动参数可知,飞行器在滑翔过程中a12和a32均恒小于零。此外本文做如下假设。
假设 1飞行器在滑翔过程中,其运动参数、弹性状态及各自的一阶导数均连续有界变化。
假设 2飞行器在滑翔过程中,设计模型中的系数a11、a12、a21、a31和a32及各自的一阶导数均连续有界变化。
假设 3飞行器在滑翔过程中,设计模型中的不确定项di,i=1,2,3均有界,且存在ρi∈R+,使得|di|≤ρi,i=1,2,3。
2 动态面IGC设计
在飞行器滑翔段IGC系统设计过程中,为了实现对飞行器弹性状态的抑制,需要对包含弹性状态的系统模型不确定项进行补偿。下面分别基于自适应方法和NDO技术,开展弹性高超声速飞行器动态面IGC系统设计。
2.1 自适应动态面IGC设计
基于假设3,可利用自适应方法对包含飞行器弹性状态的不确定项上界进行估计,进而开展动态面IGC设计。
2.1.1 设计步骤
步骤 1采用零化视线角速率制导准则,导引飞行器滑翔至预设目标位置。针对视线倾角变化率回路,设计动态面:
(18)
对动态面s1求导,并结合式(16),第一个虚拟控制量设计为
(19)
(20)
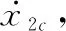
(21)
式中:τ2为滤波器常数;x2d为x2c的滤波值。
步骤 2针对攻角回路,为了跟踪视线倾角变化率回路生成的虚拟控制量x2d,设计动态面:
s2=x2-x2d
(22)
类似地,虚拟控制量可设计为
(23)
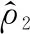
(24)
式中:ε2和σ2为大于零的设计参数。同样地,将虚拟控制量x3c通过一个一阶滤波器,即
(25)
式中:τ3为滤波器常数;x3d为x3c的滤波值。
步骤 3针对俯仰角速率回路,为了跟踪攻角回路生成的虚拟控制量x3d,设计动态面:
s3=x3-x3d
(26)
则俯仰舵偏角控制量可设计为
(27)
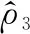
(28)
式中:ε3和σ3为大于零的设计参数。
综上所述,给出完整的自适应动态面IGC控制律为
(29)
2.1.2 稳定性分析
定义滤波误差:
yi=xid-xic,i=2,3
(30)
定义不确定项上界估计误差为
(31)
则动态面动态为
(32)
滤波误差动态为
(33)
不确定项上界估计误差动态为
(34)
定义Lyapunov函数为
(35)
式中:
(36)
则
(37)
(38)
(39)
(40)
(41)
(42)
(43)
根据假设1和假设2,经计算可知存在连续的一维正值函数g2(·)和g3(·),使得
(44)
对任意给定正数R,集合:
(45)
为一紧集。记g2(·)和g3(·)在集合U上的最大值分别为G2和G3,则可得到:
(46)
综合以上分析,可以得到:
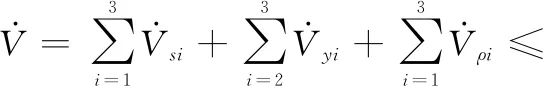
(47)
式中:
(48)
选取:
(49)
其中,κ为一正数,则有
(50)
则根据比较原理可得
(51)
2.2 基于NDO的动态面IGC设计
进一步地,考虑到可以直接对不确定项进行估计,从而消除系统不确定性的影响,下面再给出一种基于NDO的动态面IGC设计方法。以闭环系统第一个子系统为例,本文采用NDO形式如下:
(52)
(53)
定义观测器误差为
(54)
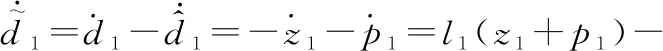
(55)
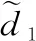
(56)
该IGC控制律中,除不确定项估计值之外的参数的具体含义与式(29)相同,并用上划线表示区分。该系统稳定性的分析过程与第2.1节基本相同,此处不再赘述。
3 仿真分析
3.1 仿真参数设置
下面开展两种IGC方法的有效性验证,弹性高超声速飞行器基本参数详见文献[2]。飞行器滑翔段质心运动和绕质心运动参数初始值设置为:v0=2 500 m/s,θ0=-2°,φ0=3°,ωz0=5°/s。受飞行器气动舵能力限制,舵偏角限幅为-20°≤δe,δc≤20°,舵偏角变化率限幅为100°/s。制导控制一体化系统设计参数设置如表1所示。

表1 制导控制系统设计参数
地面坐标系中飞行器初始位置坐标为:x0=0 km,y0=30 km,目标位置坐标设置为:xT=100 km,yT=25 km。当飞行器的滑翔高度小于25 km时仿真终止,此时飞行器与目标位置之间的距离即为脱靶量。
3.2 仿真结果
3.2.1 有效性仿真验证
首先在飞行器气动参数和大气密度处于标称条件下,验证所设计的两种IGC方法的有效性。图2~图5中红色实线(虚线)表示自适应动态面IGC方法对应的仿真结果,蓝色实线(虚线)表示基于NDO的动态面IGC方法对应的仿真结果。
图2给出了飞行器滑翔过程中质心运动参数变化情况。图2(b)中可以看出,在自适应动态面IGC方法下飞行速度倾角呈现出以较大周期轻微波动变化的特点,与之对应的,飞行器滑翔轨迹(图2(c)中红色实线)呈现出轻微的“先下压-后抬升”的特点。而基于NDO的动态面IGC方法下速度倾角经过仿真初始阶段的变化调整后,在整个仿真过程中基本保持不变,且滑翔轨迹上(图2(c)中蓝色实线)几乎保持平直。
图3(a)给出了飞行器视线倾角变化曲线,可以看出自适应动态面IGC方法下视线倾角在整个仿真过程中呈现缓慢变化特点,而基于NDO的动态面IGC方法下视线倾角几乎保持不变,这与图2(b)和图2(c)中参数变化特点相一致。图3(b)给出了飞行器-目标位置相对距离变化曲线,仿真终止时刻自适应动态面IGC方法下脱靶量为2.91 m,基于NDO的动态面IGC方法下脱靶量为3.43 m,说明本文设计的两种IGC方法均能使飞行器滑翔至预设目标位置,且均具有较高的制导控制精度。
图4给出了两种IGC方法下飞行器俯仰舵偏角(实线)和鸭翼舵偏角(虚线)的变化曲线,可以看出各舵偏角均平滑变化,说明在两种IGC方法下飞行器均可以在气动舵能力范围内完成制导控制任务。此外在仿真初始阶段,与基于NDO的动态面IGC方法相比,自适应动态面IGC方法所需的舵偏控制量相对更小。
图5给出了仿真过程中飞行器绕质心运动参数变化曲线,可以看出两种方法下飞行器姿态角变化均平稳有界。
3.2.2 鲁棒性仿真验证
为了进一步验证本文设计的两种IGC方法的鲁棒性,将气动力系数、气动力矩系数和大气密度作为检验鲁棒性的偏差因素,其中气动力系数和气动力矩系数偏差幅值为±20%,大气密度的偏差幅值为±30%,以拉偏后的参数作为实际仿真参数,开展8种参数偏差组合下的仿真验证。表2给出了不同参数偏差组合下仿真结果标识线型和终端时刻脱靶量。

表2 不同参数偏差组合下的脱靶量
图6给出了不同参数偏差组合下两种IGC方法的飞行速率仿真结果。图7给出了不同参数偏差组合下两种IGC方法对应的滑翔轨迹仿真结果,可以看出对于自适应动态面IGC方法,气动力矩系数的偏差状态对滑翔轨迹的影响不大,而大气密度和气动力系数的偏差状态对滑翔轨迹中后段的下压程度有影响,即大气密度或气动力系数处于负极限偏差时,滑翔轨迹中后段的下压程度更大,这是因为此时飞行器在纵向的实际升力进一步小于飞行器重力,从而增大了轨迹下压程度。而当大气密度和气动力系数均处于负极限偏差时(对应⑦组和⑧组),滑翔轨迹中后段的下压程度过大,导致飞行器滑翔高度提前达到仿真终止条件而无法达到预设航程,脱靶量超过了10 km。文献[30]也得到了类似的仿真结果。对于基于NDO的动态面IGC方法,不同参数偏差组合下滑翔轨迹的偏离程度不大。
图8和图9给出了不同参数偏差组合下两种IGC方法对应的俯仰舵偏角和攻角的仿真结果,可以看出当大气密度或气动力系数处于负极限偏差时,两种方法下飞行器在滑翔中后段均需要更大的攻角,这是因为在大气密度或气动力系数处于负极限偏差时,需要更大的攻角来弥补飞行器升力的不足,从而实现对视线倾角变化率的动态控制。
从表2可以看出:
(1) 不同参数偏差组合下,两种IGC方法的最大脱靶量均出现在⑦组,即当所有参数都处于负极限偏差时;
(2) 对于自适应动态面IGC方法,除了⑦组和⑧组外,其他参数偏差组合下的制导控制精度均较高,而对于基于NDO的动态面IGC方法,⑦组和⑧组下的脱靶量都控制在了40 m以下,且其他参数偏差组合下的制导控制精度同样较高,这说明基于NDO的动态面IGC方法对于参数偏差具有更好的鲁棒性。
下面结合滑翔轨迹仿真结果,对造成两种IGC方法呈现鲁棒特性差异的原因进一步分析。自适应动态面IGC方法利用自适应律对系统不确定项上界进行估计,能够较好地处理不确定性,然而该方法无法实时估计并补偿不确定性,因此具有更强的保守性,使得仿真初始阶段生成的舵偏角指令幅值有限,导致飞行器需要在滑翔中后段进一步调整速度方向,因而滑翔轨迹呈现出了轻微的“先下压-后抬升”的特点,当大气密度和气动力系数均处于负极限偏差时,滑翔高度便提前达到了仿真终止条件,脱靶量较大。而基于NDO的动态面IGC方法利用NDO技术,可以实时地、更高精度地估计包含参数拉偏和弹性状态在内的不确定性并补偿其影响,仿真初始阶段生成的舵偏角指令幅值够大,确保飞行器的视线倾角能够及时调整到位并基本保持恒定,滑翔轨迹基本保持平直,从而对参数偏差表现出了更好的鲁棒特性。
4 结 论
针对弹性高超声速飞行器滑翔段IGC系统设计问题,基于自适应方法和NDO技术,设计了两种动态面IGC方法。仿真结果表明所设计的两种IGC方法均能使弹性高超声速飞行器滑翔至目标位置附近。其中,自适应动态面IGC方法由于具有更强的保守性,使得飞行器滑翔轨迹呈现出轻微的“先下压-后抬升”的特点,导致该方法的制导控制精度更容易受大气密度和气动力系数偏差状态的影响。而基于NDO的动态面IGC方法采用了NDO技术,可以实时准确地估计包含参数拉偏和弹性状态在内的不确定性并补偿其影响,使得滑翔轨迹几乎保持平直,对参数偏差表现出更好的鲁棒性能。本文为弹性高超声速飞行器IGC系统设计问题提供了具有参考价值的设计方法。
